折线数轴上的动点问题探究
张 哲
(苏州工业园区星海实验中学,江苏苏州,215000)
以数轴为载体的动点问题,对于刚升入初中的学生来说,是重难点问题.由于涉及复杂的行程问题和方程问题,综合性较强,因此对学生综合分析问题和解决问题的要求比较高.折线数轴上的动点问题又是对数轴上的动点问题的进一步加深和拓展,动点从匀速运动变成了变速运动,在各个路段的计算变得复杂,难度进一步加大.为了让学生们熟练掌握折线数轴上的动点问题,深入了解动点在折线数轴上的运动规律和动点之间运动变化的全过程以及寻求它们的等量关系,下面以一道折线数轴上的动点问题及其变式为例剖析这类问题的解法和技巧.
1 典型案例呈现
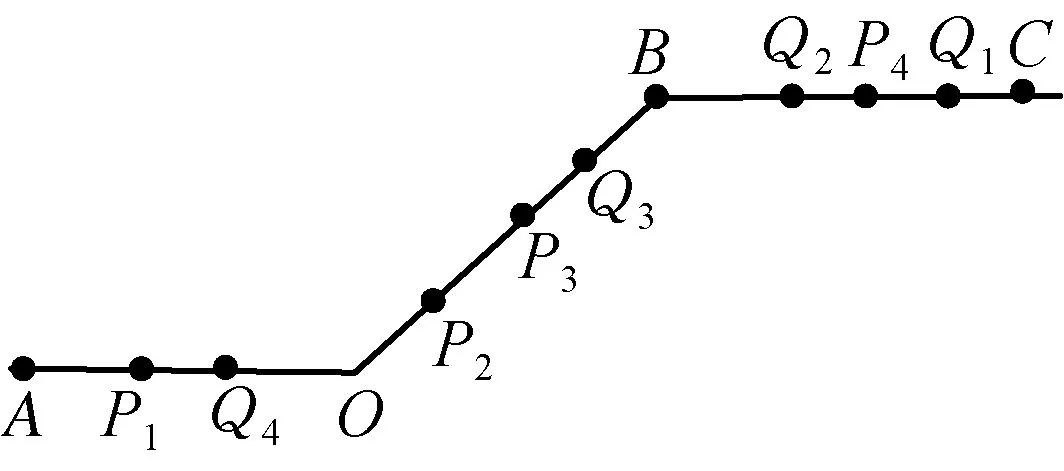
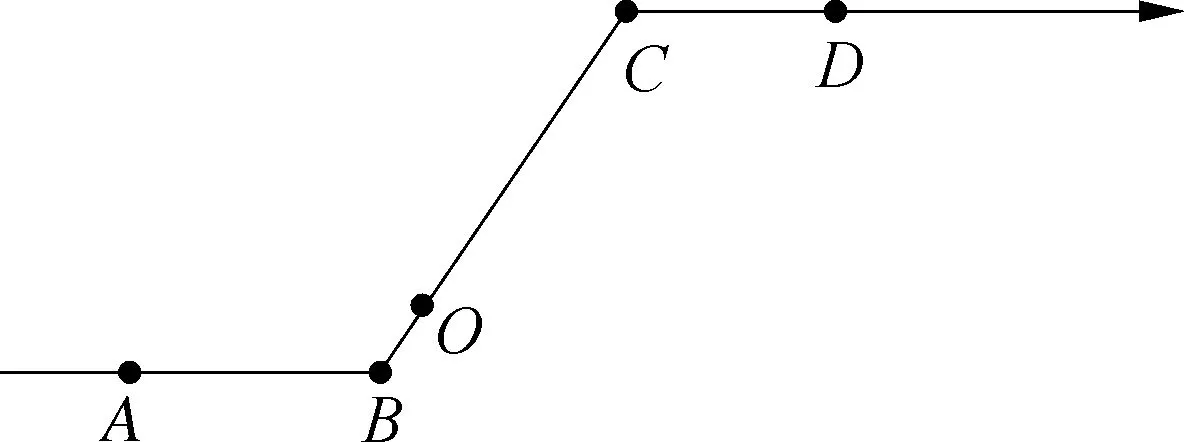
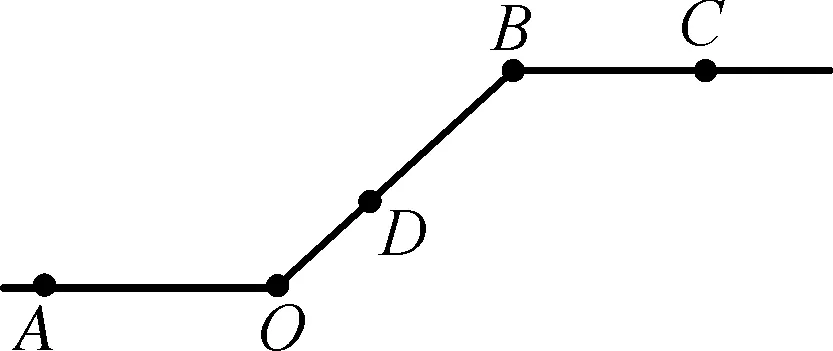
例题如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示-10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位.动点P从点A出发,沿着“水平路线”射线OA向正方向运动,速度为2个单位/秒,“上坡路段”从O到B速度变为“水平路线”速度的一半,之后立刻恢复原速;动点Q从点C出发,以1单位/秒的速度沿着“水平路线”射线BC向负方向运动,从“下坡路段”点B运动到点O期间速度变为“水平路线”速度的2倍,之后也立刻恢复原速.设运动的时间为t秒.问:

(1) 动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3) 求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
在解决该问题之前,我们需要明确几个基本概念及知识点.
我们知道数轴是规定了原点、正方向、单位长度的直线.三个要素缺一不可.
折线数轴只是在其基础上折了一下,因此同样具备这三个要素.
不妨将其定义为折线数轴是规定了原点、正方向、单位长度的折线.
2 折线数轴相关知识
(1) 折线数轴上两点之间的距离.用两点所表示的数差的绝对值表示,如数轴上点A,B所表示的数是A,B,则AB=|A-B| 或|B-A|.
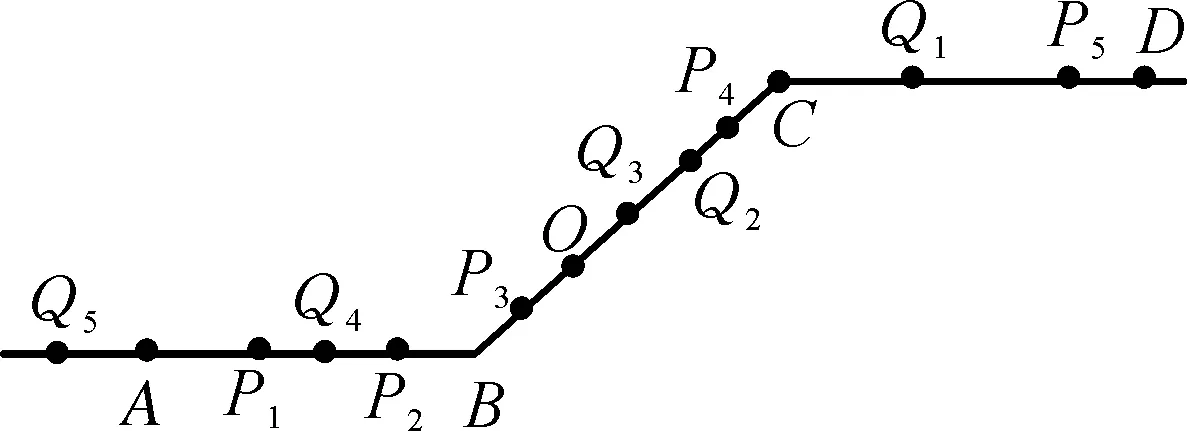
(2) 如图,规定水平路线为射线OA,BC,上坡路线为向量OB,下坡路线为向量BO.同一个动点在这三个路段的运动速度的关系为v上坡 (3) 规定向右为正方向,并将向右运动的速度看作正速度,而向左为负方向,并将向左运动的速度看作负速度. (4) 折线数轴上的动点表示法.用代数式来表示,就是起点所表示的数加上或减去动点运动的距离,向正方向为加,负方向为减,如,数轴上点A对应的数为-2,点P从点A出发,以每秒4个单位长度的速度向右运动,设运动时间是t,则点P所表示的数是-2+4t.若以每秒4个单位长度的速度向左运动,设运动的时间是t,则点P所表示的数是-2-4t. (1) 明确不动的点坐标,动点的起点坐标及其动点运动方向及速度,并表示出水平路段,上下坡路段的距离;(2) 用含有时间t的代数式表示动点的运动路程;(3) 寻求等量关系,列出方程.判断是否需要分类讨论,如果存在多种情况,逐一绘制图形,寻求各自的等量关系,列出方程求解;(4) 根据实际情况来检验方程的解. 下面结合折线数轴的知识、解题步骤和方法来解决例题. 解析:(1) 动点P从点A运动至C分成三段,分别为AO、OB、BC, AO段时间为5 s,OB段时间为10 s,BC段时间为4 s, ∴动点P从点A运动至C点需要时间为5+10+4=19(秒). (2) 易知P、Q两点在OB上相遇. 方法一:根据相遇时所走的总路程等于全程列等量关系式. 方法二:根据相遇时所走的时间相等列等量关系式. 方法三:根据点P、点Q在OB段运动的总路程等于10列等量关系式. (3) 已知|PO|=|QB|,其中O、B为定点,P、Q为动点, 方法一:以点P、点Q在各路段运动的拐点时间来分类. ① 当O 10-2t=8-t,解得t=2; ② 当5≤t<8,点P在OB上,点Q在CB上运动时, ③ 当8≤t<13,P在OB上,Q在OB上运动时, t-5=2(t-8),解得t=11; ④ 当13≤t<15时,P在OB上,Q在OA上运动时, t-5=t-8-5+10,t无解; ⑤ 当15≤t<19时,P在BC上,Q在OA上运动时, 2(t-5-10)+10=t-8-5+10,解得t=17; ⑥ 当t>19,P在C的右侧,Q在OA或A的左侧上运动时, 2(t-5-10)+10=t-8-5+10,解得t=17;不符合要求, 方法二:分析点P、点Q在各个路段的运动路程可以分四种情况讨论. ① 当点P在AO,点Q在BC上运动时,依题意得: 10-2t=8-t,解得t=2; ② 当P在OB上,Q在BC上运动时, ③ 当点P、Q两点都在OB上运动时, t-5=2(t-8),解得t=11; ④ 当P在BC上,Q在OA上运动时, t-8-5+10=2(t-5-10)+10,解得t=17. 点评:对于折线数轴上的动点问题,首先要弄清楚各个点的整个运动过程,由于变速运动各段速度不同,在计算路程时必须分路段讨论.本题第二问是相遇问题,根据相遇时两点的运动时间相等或是两点运动的路程和等于总路程,或是折线数轴上的部分路段的关系找到了三种等量关系来列方程.第三问的难点在于如何分类讨论,同样以两种方法来解决,第一种是以时间为节点,根据某段时间点P、点Q在AO、OB、BC的位置求出相应的距离,这样的分类讨论不重不漏,条理清晰;第二种方法是经过初步的分析,得出可能出现的点P、点Q的位置求出相应的距离,解答过程更简洁. 进一步变式思考:对于一道动点问题的探究,我们不能只停留在多种方法的解决上,还要对题目所给条件和结论进行深度思考.对题目进行变式再解决,形成折线数轴上动点问题的解决通法. 如果把P、Q两点分别到两定点的距离相等变为到同一定点的距离相同,把相遇问题变成追及问题,我们可以得到变式1. 变式1如图,数轴上,点A表示的数为-7,点B表示的数为-1,点C表示的数为9,点D表示的数为13,在点B和点C处各折一下,得到条“折线数轴”,我们称点A和点D在数上相距2O个长度单位,动点P从点A出发,沿着“折线数轴”的正方向运动,同时,动点Q从点D出发,沿着“折线数轴”的负方向运动,它们在“水平路线”射线BA和射线CD上的运动速度相同均为2个单位/秒,“上坡路段”从B到C速度变为“水平路线”速度的一半,“下坡路段”从C到B速度变为“水平路线”速度的2倍.设运动的时间为t秒,问: (1) 动点P从点A运动至D点需要时间为秒; (2)P、Q两点到原点O的距离相同时,求出动点P在数轴上所对应的数; (3) 当Q点到达终点A后,立即调头加速去追P,“水平路线”和“上坡路段”的速度均提高了1个单位/秒,当点Q追上点P时,直接写出它们在数轴上对应的数. 解析:(1) 动点P从点A运动到点D所需时间为15秒. (2) 已知|PO|=|QO|, 方法一:以点P、点Q在各路段运动的拐点时间来分类. ① 当点P在AB,点Q运动到点D前,0≤t<2时,7-2t=13-2t,t无解 ② 当点P在AB,点Q运动到点O前,2≤t<3时,7-2t=13-4-4(t-2),t=5,不符合. ④ 当点P在OC,点Q在BA或A左侧时,4.5≤t<13时,6+(t-3)-7=4+10+2(t-4.5)-13,t=4不符合. ⑤ 当点P在CD或D右侧,点Q在BA或A左侧时,t>13时,6+10+2(t-13)=4+10+2(t-4.5)-13,t无解. 方法二:仍可以按照分析点P、点Q在各段的路程来计算.由于篇幅所限省略. (3) 点P、点Q先是相向而行,点Q到达点A返回过程是同向而行,成了追及问题.当Q追上P时,|PO|=|BO|.点Q到达点A所需时间为7.5秒,此时点P运动的路程为10.5,到达的点是3.5,点P到达点C所需时间为13秒,此时点Q到达的点是6,故点Q在CD上追上点P,此时P运动的路程为6+10+(t-3-10)×2=2t-10,故PO=2t-17,Q运动的路程为20+6+10+(t-7.5-2-5)×3=3t-7.5,QO=3t-7.5-20-7=3t-34.5,2t-17=3t-34.5,解得t=17.5, 此时点P表示的数为18,点Q表示的数为18. 如果让定点的值是未知数,P、Q两动点的距离是定值,我们可以得到变式2. 变式2如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”,图中点A表示-20,点B表示m,点C表示40,我们称点A和点C在数轴上相距60个长度单位,用式子表示为AC=60,动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,运动到B点停止;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后立刻恢复原速,当P停止运动后,Q也随之停止运动,设运动的时间为秒,问: (1)BC=(用含m的式子表示); (2) 若P、Q两点在数轴上点O至点B之间的D点相遇,D点表示10,求m; (3) 在(2)的条件下,当PQ=40时,求t. 解析:(略) 数轴是数学解题的有力工具,而数轴上点的运动问题体现了数形结合的有机结合.对于折线数轴上的动点问题,我们要化动为静,找到动点满足条件的静止位置.一般有两种解题思路.一种是根据“形”的关系来分析寻找等量关系.如例1、变式1中的第二、三两问都是根据点之间的行程路程,利用行程的路程差的数量关系列方程求解;另一种是从“数”的方面寻找等量关系,如变式2的第三问就是利用各动点在数轴上内在关系进行列方程求解. 在教学中,为了方便学生理解和掌握,教师首先要采用拐点时间来分类,借助数轴将动点在各个路段的时间算出来,再以时间来分类,确定点的坐标或是运动路程.在学生熟练掌握这一方法后,再尝试直接分析动点在数轴的可能位置来分类.分析的过程中,画出对应的图形,根据所画的图形,结合题目所给条件分析,利用方程求解得到的结果.这正是“数形合一”的精彩体现. 总之,关于折线数轴上的问题,虽然题目形式多样,但是万变不离其宗,教师要引导学生回归基础,把握好“数轴”这一本质,总结解题方法,注重通性通法,形成解题能力.3 折线数轴上的动点问题的解题步骤和方法

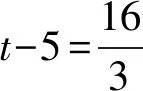
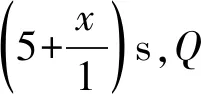
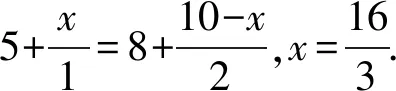
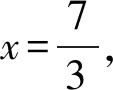
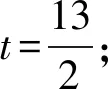
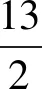
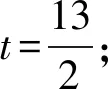
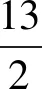
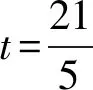
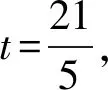
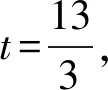
4 结束语

