初中数学中关于“圆”的解题策略探索

玉 兰

(内蒙古通辽市库伦旗第四中学，内蒙古通辽，028299)

圆形在生活中十分常见，也是数学中的一个特殊的有规则图形，教师应在执教过程中，引导学生正确理解圆的基本定理，并结合圆形的特殊性质，更好地解决圆形问题的相关知识.教师还应注意激发学生的数学知识学习兴趣，让学生能够自发自觉地探究关于圆形问题的解题策略，启发学生更加深入地思考相关圆形的知识.

1 利用“圆”的对称性解题

作为轴对称图形、中心对称图形及旋转对称图形，圆形上任何一条直径的所在直线都是其对称轴，且圆心是其对称中心.教师可以通过动手实作的方式，让学生进一步对圆的对称性进行理解.教师可以让学生将手中的圆形沿着中心线进行任意折叠，会发现无论从哪一个方向进行折叠，都会使圆形变成一个半圆形，教师可以借此启发学生认知；通过圆心进行折叠，一条折痕就是直径，而直径的一般即为半径，一条圆弧和经过圆弧这条两端的两条半径所围成的图形叫扇形.教师可以以此为学习基础，将学习知识点进行深入挖掘，包括引导学生认知圆形周长及面积，这会顺理成章地完成知识内容的迁移，让学生能够进一步理解圆的对称性.

例1学生甲和学生乙在沙滩上玩耍，需要在沙滩上画出一个圆形，但二人手中均没有工具，那么，应如何在沙滩上画出圆形？结合圆的对称性进行分析，圆是在平面内到一定点的距离等于定长的点的轨迹，而圆心被称为定点O，半径Oa则被称为定长，由于定长的点的集合与到点的距离相等，所以，学生甲可以在原地旋转，将学生甲设置为O点，并拉动学生乙的手臂，将学生乙设置为a点，让学生乙绕着学生甲在沙滩上走一圈，学生乙与学生甲之间的距离即为Oa，当绕到点b时，就会形成一个半圆，学生乙继续前行，直到走到a点，这自然就会形成一个圆形(见图1).教师通过这种与生活内容相结合的，甚至与每个人都息息相关的模式开展教学，这会增加学生的代入感，让学生可以更好地理解圆的对称性这一特征.教师也可以让同桌两人在室外场地还原画圆圈的场景，让学生能够通过实践进一步理解圆的对称性的特点，促进学生进行巩固记忆.

图1

2 利用“圆心角”解题

在等圆或同圆中，圆心角相等则其所对应的弦及所对应的弧都是相等的.在等圆或同圆中，若两条弦相等、两条弧相等、两个圆心角相等中只要有一个概念成立，则说明另外两个概念也是成立的.教师在引导学生理解了圆心角的基本概念后，应通过案例对学生进行教学引导，以此提高学生的圆心角知识应用能力.

例2如图2-1，已知在⊙O中，∠A=35°，OB⊥OA，求∠COD的度数.

图2-1

解题：将OC连接，在Rt△AOB中，∠A=35°，∴∠B=55°，又∵OB=OC，∴180°-2∠B=∠COB=70°，∴∠COD=90°-∠COB=90°-70°=20°.在本问题中，将OC相连，在求圆心角度数的基础上求解，以此对圆心角的概念进行巩固性认知.

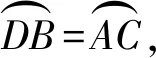
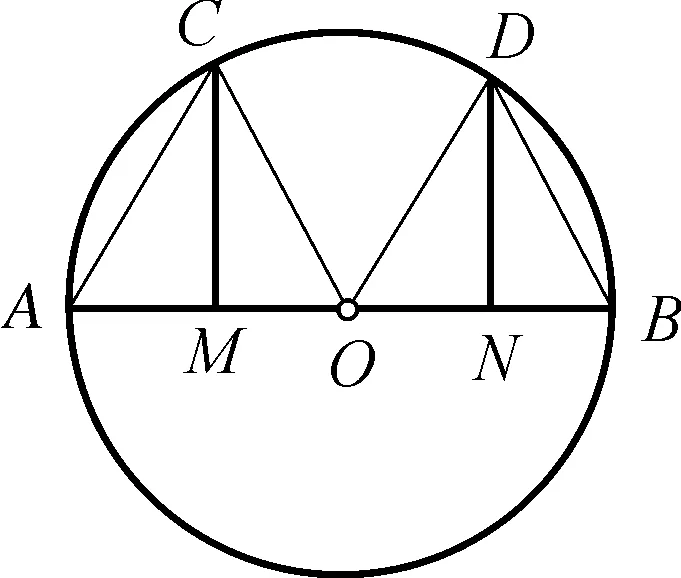
图2-2

解法1：若证明弧相等，可以将BD、OD、OC、AC进行连接，N、M分别为BO、AO的中点，AB⊥CM、AB⊥DN，∴BD=OD、OC=AC，又∵OD=OC，∴BD=AC，所以弧度相等.

解法2：为拓展学生的思维模式，教师还可以鼓励学生连接OD和OC进行证明.由于N、M分别是BO、AO的中点，∴BN=ON、AM=OM，∵OB=OA，∴ON=OM，∵AB⊥CM，AB⊥DN，OD=OC，∴Rt△DON≌Rt△COM，∴∠DOB=∠COA，所以弧度相等.

这一案例题目的难度并不强，但其解题方法较为灵活，而通过基本的辅助线可以提高学生的发散思维素养.

3 利用“垂径定理”解题

利用垂径定理进行解题，大都结合勾股定理，以及弦心距、弦长、半径间的运算，为提高学生对垂径定理的解题能力，教师可以通过案例教学的方式启发学生学习，并将案例进行组合，让学生能够通过掌握一种解题方法，进而对相同类型问题进行解题的素养，提高学生举一反三的能力，以及知识迁移能力，促进学生发散思维素养的不断提高.

例4⊙O的弦CD与直径AB在E点相交，∠DEB=30°，EB=6，AE=2，求弦CD的长度.(见图3-1)

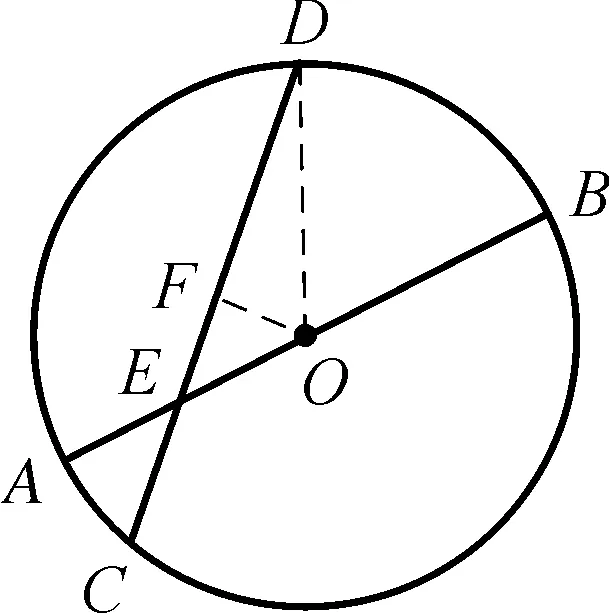
图3-1

图3-2

变式2⊙O的弦为AB，AB上的一点为M，若OM=10 cm、MB=8 cm、AB=20 cm，求⊙O的半径.(见图3-3)教师应结合垂径定理，启发学生进行分析，通过计算可知，⊙O的半径等于14.

图3-3

在此基础上，教师应鼓励学生以垂径定理解决综合应用问题.

图3-4

学生在对本题进行解题后，能够有效提高对垂径定理的应用能力，还可以根据题意做出辅助线，以此对构造出的直角三角形进行分析，会有效提高本题的解题效率.

4 利用“弦心距”解题

在一个圆中，圆心与该圆的任一弦距离即这一弦的弦心距，在等圆或同圆中，弦心距及弦都是相等的，若两条弦不相等，则其弦心距也是不相等的，弦心距较小反而说明弦大.教师在引导学生理解弦心距定理后，应结合实际问题启发学生进行深入思考，确保学生通过解题对数学定理进一步认识，并以此提高学生将理论知识转换为实践思维的能力，使学生的数学思考能力可以获得不断突破[3].

例5如图4，在⊙O中，弦EF=CD，直径为10 cm，CD⊥OA于A，EF⊥OB于B，EF=8 cm，求OA的长.在对本问题进行解决的过程中，教师应提醒学生，在解决弦心距、弧、弦问题的环节，应做出弦心距或半径，确保半径、弦心距、弦的一半构成直角三角形，并注意在等圆或同圆中，将弦心距、弧、弦、圆心角的关系进行解读.可以将OF连接，EF=CD，CD⊥OA、EF⊥OB，∴BF=BE，AD=AC，OB=OA，∴直径为10 cm，而OF则为5 cm，∴OA=3 cm.

图4

图5

利用不同方法进行解题，有利于提高学生对弦心距概念的理解能力，也可以让学生从不同角度思考数学问题，对促进学生数学综合思维素养的提高大有裨益.

5 结语

总而言之，在学习关于“圆”知识内容的过程中，教师应注意结合不同的案例帮助学生进行分析，这会有助于学生巩固对相关数学概念问题的理解，也可以让学生能够通过分析数学概念，对数学应用问题进行探究，确保学生能够运用数学思维发现数学问题、分析问题、解决问题.尤其对于“圆”知识点的学习，更应对与圆有关的所有定理有一个充分的掌握，使学生能够更加高效地解决关于“圆”的问题，帮助学生从多元视角进行解题.