预李H-伪代数的推广*

刘琳琳

(河南工学院 理学部,河南 新乡 453003)

0 引言

伪代数作为共形代数[1]的自然推广,与非线性演化方程中Ritt-哈密顿形式的微分李代数有密切关系[2]。伪代数的概念最早由Bakalov、D'Andrea和Kac在伪张量范畴中引入[3]。简单来说,伪张量范畴就是一个带有多重线性映射且满足相应复合法则的范畴。我们考虑特殊的伪张量范畴M*(H),设H是一个余交换的Hopf代数,伪张量范畴M*(H)中的对象为左H-模,并且带有特殊的伪张量结构

2001年,Kac等人在文献[3]中定义且研究了伪张量范畴M*(H)中的李代数和结合代数,分别称为李H-伪代数和结合H-伪代数。随后Wu在这个范畴中定义了预李(或左对称)代数和Leibniz代数,分别称为预李(或左对称)H-伪代数[4]和LeibnizH-伪代数[5]。2012年,Sun通过H-模同态将李(特别地,结合)H-伪代数推广到Hom的情形,称为Hom-李(特别地, Hom-结合)H-伪代数[6]。基于此,本文主要研究Hom-预李H-伪代数以及其构造。

本文所有的向量空间、线性映射和张量积都是在特征为0的域K上。若无特别声明,H均表示余交换的Hopf代数,对于任何向量空间V以及V中的元素f、g、h,我们定义(13)(f⊗g⊗h)=h⊗g⊗f,(23)(f⊗g⊗h)=f⊗h⊗g以及σ(f⊗g)=g⊗f。类似地,还有符号(12)、(123)、(132)等。

1 预备知识

本节我们回顾伪代数的相关定义。

定义1[4]预李H-伪代数是一个二元组(A,*),其中A是一个左H-模, *∈HomH⊗H(A⊗A,(H⊗H)⊗HA)(*称为伪积),满足

(x*y)*z-x*(y*z)=((12)⊗Hid)((y*x)*z-y*(x*z))

其中x,y,z∈A。

定义2[6]Hom-结合H-伪代数是一个三元组(A,*,α),其中A是一个左H-模, *∈HomH⊗H(A⊗A,(H⊗H)⊗HA),α∈HomH(A,A),满足

(x*y)*α(z)=α(x)*(y*z)

其中x,y,z∈A。

定义3[6]Hom-李H-伪代数是一个三元组(L,[*],α),其中L是一个左H-模,[*]∈HomH⊗H(L⊗L,(H⊗H)⊗HL)([*]称为伪括号),α∈HomH(L,L),满足斜-交换性:[a*b]=-(σ⊗Hid)[b*a],Hom-雅可比等式:[[a*b]*α(c)]=[α(a)*[b*c]]-((12)⊗Hid)[α(b)*[a*c]],其中a,b,c∈L。

2 Hom-预李H-伪代数

下面给出Hom-预李H-伪代数的定义。

定义4左(特别地,右)Hom-预李H-伪代数是一个三元组(A,*,α),其中A是一个左H-模,*∈HomH⊗H(A⊗A,(H⊗H)⊗HA),α∈HomH(A,A),满足

(x*y)*α(z)-α(x)*(y*z)=((12)⊗Hid)((y*x)*α(z)-α(y)*(x*z))

(特别地,(x*y)*α(z)-α(x)*(y*z)=((23)⊗Hid)((x*z)*α(y)-α(x)*(z*y)))

其中x,y,z∈A。

注释:(1)如无特别说明,下文所说的Hom-预李H-伪代数均指左的情况。

(2)显然,任一Hom-结合H-伪代数都是Hom-预李H-伪代数。

(3)当H=K时,Hom-预李H-伪代数即为预李H-伪代数;当α=id时,Hom-预李H-伪代数便退化为Hom-预李代数。

Hom-预李H-伪代数(A,*,α)称为可乘的,若[α(a),α(b)]=(idH⊗2⊗Hα)[a,b]。例如,一个预李H-伪代数关于α=id∈HomH(A,A)是一个可乘的Hom-预李H-伪代数。

定义5设(A,*,α)和(A′,*′,α′)是两个Hom-预李H-伪代数。若对于任意的a,b∈A满足f∘α=α∘f和(idH⊗2⊗Hf)(a*b)=f(a)*′f(b),则称H-线性映射f:(L,*,α)→(L′,*′,α′)为Hom-预李H-伪代数同态。

接下来我们给出左和右Hom-预李H-伪代数之间的关系。

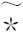
证 对于任意的x,y,z∈A,我们有

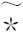
=((13)⊗Hid)(α(z)*(y*x)-(z*y)*α(x))

=((13)(12)⊗Hid)(α(y)*(z*x)-(y*z)*α(x))

=((123)⊗Hid)(α(y)*(z*x)-(y*z)*α(x))

=((123)⊗Hid)(α(y)*(z*x)-(y*z)*α(x))

=((23)⊗Hid)((13)⊗Hid)(α(y)*(z*x)-(y*z)*α(x))

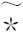
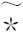
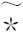
下面我们给出Hom-预李H-伪代数的构造定理。

定理1设(A,*)是一个预李H-伪代数,α是A上的自同态(即α(x)*α(y)=(id⊗Hα)(x*y))。定义x*αy∈HomH(A⊗A,(H⊗H)⊗HA)为

x*αy=α(x)*α(y)=(id⊗Hα)(x*y)

则(A,*α,α)是一个可乘的Hom-预李H-伪代数。

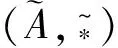
是一个可乘的Hom-预李H-伪代数同态。

证因为α是A上的自同态,则

(x*αy)*αα(z)=(id⊗Hα)(x*y)*αα(z)

=(id⊗Hα)((id⊗Hα)(x*y)*α(z))=(id⊗Hα2)((x*y)*z)

类似地,有α(x)*α(y*αz)=(id⊗Hα2)(x*(y*z))。所以

(x*αy)*αα(z)-α(x)*α(y*αz)=(id⊗Hα2)((x*y)*z-x*(y*z))

=(id⊗Hα2)((12)⊗Hid)((y*x)*z-y*(x*z))

=((12)⊗Hid)(id⊗Hα2)((y*x)*z-y*(x*z))

=((12)⊗Hid)((y*αx)*αα(z)-α(y)*α(x*αz))

另一方面,α(x)*αα(y)=(id⊗Hα)(α(x)*α(y))=(id⊗Hα)(x*αy)。故(A,*α,α)是一个可乘的Hom-预李H-伪代数。因为f∘α=β∘f,故

(id⊗Hf)(x*αy)

=(id⊗Hf)(id⊗Hα)(x*y)=(id⊗Hf∘α)(x*y)

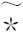
因此f是一个可乘的Hom-预李H-伪代数同态。

更一般地,我们可以得到一类可乘的Hom-预李H-伪代数。

定理2设(A,*,α)是一个可乘的Hom-预李H-伪代数,则

An=(A,*n=(id⊗Hα2n-1)∘*,β=α2n)

也是可乘的Hom-预李H-伪代数。

证注意到A0=(A,*,α),A1=(A,*1=(id⊗Hα)∘*,β=α2),以此类推,可知An+1=(An)1。因此我们只需要验证n=1的情形即可,即证明A1是一个可乘的Hom-预李H-伪代数。对于任意的x,y,z∈A,可知

(x*1y)*1β(z)=(id⊗Hα)(x*y)*1α2(z)=(id⊗Hα2)((x*y)*α(z)),

β(x)*1(y*1z)=α2(x)*1(id⊗Hα)(y*z)=(id⊗Hα2)(α(x)*(y*z))

因此我们有

(x*1y)*1β(z)-β(x)*1(y*1z)

=(id⊗Hα2)((x*y)*α(z)-α(x)*(y*z))

=(id⊗Hα2)((12)⊗Hid)((y*x)*α(z)-α(y)*(x*z))

=((12)⊗Hid)((y*1x)*1β(z)-β(y)*1(x*1z))

另一方面,易证*1∈HomH⊗H(A⊗A,(H⊗H)⊗HA),β∈HomH(A,A),故结论成立。

3 从Hom-预李H-伪代数到Hom-李H-伪代数

本节我们从Hom-预李H-伪代数出发来构造Hom-李H-伪代数。

定理3设(A,*,α)是一个可乘的Hom-预李H-伪代数,定义伪括号[*]为

[x*y]=x*y-(σ⊗Hid)(y*x),∀x,y∈A

则(A,[*],α)是一个可乘的Hom-李H-伪代数。

证对于任意的x,y∈A,我们有

[x*y]=x*y-(σ⊗Hid)(y*x)

=-(σ⊗Hid)(y*x-(σ⊗Hid)(x*y))

=-(σ⊗Hid)[y*x]

因此伪括号[*]满足斜-交换性。下证Hom-雅可比等式,对于任意的x,y,z∈A,我们有

[α(x)*[y*z]]=α(x)*(y*z)-((123)⊗Hid)((y*z)*α(x))

-((23)⊗Hid)(α(x)*(z*y))+((13)⊗Hid)((z*y)*α(x))

上式中交换x和y的位置可得

[α(y)*[x*z]]=α(y)*(x*z)-((123)⊗Hid)((x*z)*α(y))

-((23)⊗Hid)(α(y)*(z*x))+((13)⊗Hid)((z*x)*α(y))

类似地,

[[x*y]*α(z)]=(x*y)*α(z)-((132)⊗Hid)(α(z)*(x*y))

-((12)⊗Hid)((y*x)*α(z))+((13)⊗Hid)(α(z)*(y*x))

利用以上等式可得

[α(x)*[y*z]]-((12)⊗Hid)[α(y)*[x*z]]-[[x*y]*α(z)]

=α(x)*(y*z)-((123)⊗Hid)((y*z)*α(x))-((23)⊗Hid)(α(x)*(z*y))

+((13)⊗Hid)((z*y)*α(x))-((12)⊗Hid)(α(y)*(x*z))

+((23)⊗Hid)((x*z)*α(y))+((123)⊗Hid)(α(y)*(z*x))

-((132)⊗Hid)((z*x)*α(y))-(x*y)*α(z)+((132)⊗Hid)(α(z)*(x*y))

+((12)⊗Hid)((y*x)*α(z))-((13)⊗Hid)(α(z)*(y*x))

=α(x)*(y*z)-(x*y)*α(z)-((123)⊗Hid)((y*z)*α(x)-α(y)*(z*x))

-((23)⊗Hid)(α(x)*(z*y)-(x*z)*α(y))

+((13)⊗Hid)((z*y)*α(x)-α(z)*(y*x))

-((12)⊗Hid)(α(y)*(x*z)-(y*x)*α(z))

-((132)⊗Hid)((z*x)*α(y)-α(z)*(x*y))

=0

证毕。