电池包上壳体可靠性评估及结构优化

方 骏，潘 涛，吕雪伟，王东生，3，邢时超

(铜陵学院 1.机械工程学院；2.工程液压机器人安徽普通高校重点实验室；3.铜陵市增材制造重点实验室，安徽 铜陵 244100)

结构仿真与优化是工程设计初期的重要内容，结构仿真主要包括结构强度、刚度分析，根据仿真的结果，可为结构优化设计提供准确的方案，增强产品的综合性能[1-2]。

目前，新能源汽车的电池包上壳体结构主要有四种，如“土”字型、“凹”字型、“T”字型和“滑板”式，本文主要结合某企业在设计初期“T”字型电池包结构[3]，从刚度、强度、模态三个方面进行研究电池包结构的可靠性[4]，进而为后续的优化设计提供方案。

1 有限元模型

1.1 结构及简化

上壳体的细小特征较多，如倒角和圆角，有限元分析之前，可去除较小特征，保留上壳体的较大特征[3]。上壳体和其他部分采用螺栓固定连接，底座侧面留有线孔和散热孔。本文运用有限元技术将该电池包上壳体模型简化成T字型结构，这种方式的简化能有效提高计算效率，节约了有限元分析时间，电池包整体简化后的模型如图1所示。

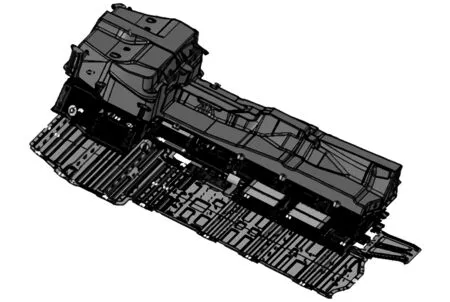
图1 简化后的电池包箱体数模

1.2 模型属性

结合上壳体的特点，简化的电池包上壳体，采用四面体划分网格，其质量为21.53kg，单元尺寸为5mm，节点数为257 949个。

该电池包上壳体为6061-T6铝合金[5]，主要材料属性如表1所示。

表1 材料属性

2 刚度分析

2.1 电池包结构刚度分析

采用CATIA有限元分析模块模拟计算，此次对于该零件的刚度载荷情况如表2所示，对应位移云图如图2、图3及图4所示。

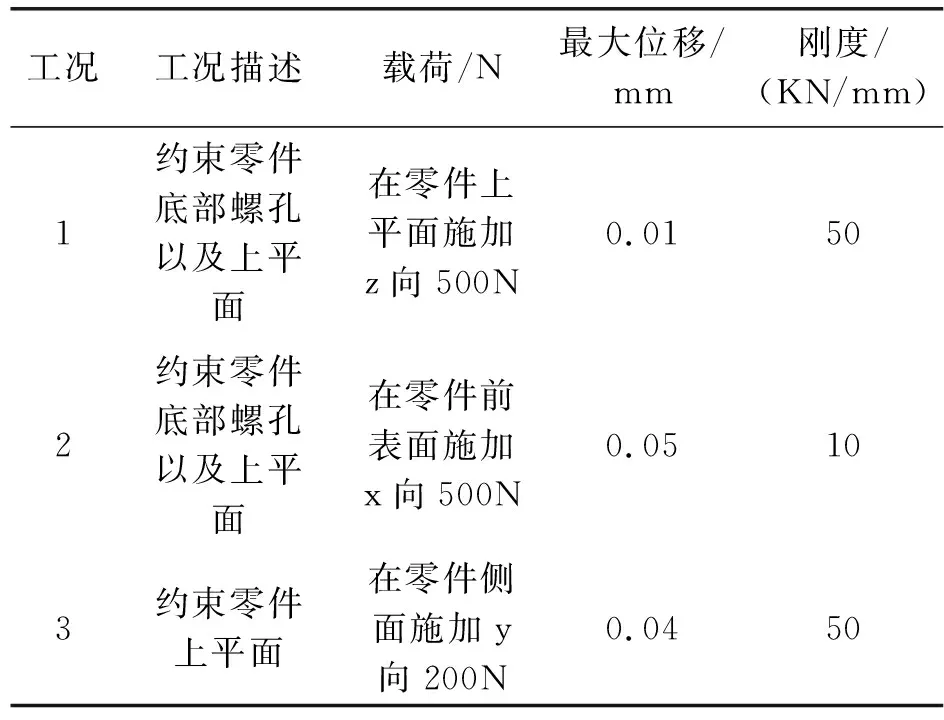
表2 工况要求

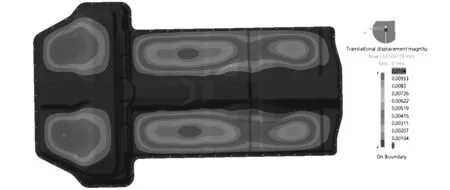
图2 工况1 正面受力载荷云图

图3 工况2 前表面受力载荷云图

图4 工况3 侧面受力载荷云图

由图2、图3及图4工况的有限元模型位移云图结果可知，该电池上壳体三种典型工况下的最大位移均小于0.1mm，刚度均小于100(KN/mm)，其中，在零件前表面施加x向载荷500N时，位移最大值为0.05mm，最大刚度值为50(KN/mm)。

3 强度分析

3.1 电池箱上壳体结构强度分析

电池包上壳体是电池箱的重要组成部分，上壳体的强度会影响电池箱的整体性能，进而损坏内部的电池，极有可能会引起电池的爆炸。因此，就需要电池包箱上壳体具有足够的强度，此次考虑到车辆在道路中受外界环境多方面的载荷激励影响，需要计算电池箱上壳体分别在非平整路面直行、急刹车和急拐弯的极限强度[7-8]，按照强度的云图及数据，提出电池箱上壳体的优化设计方案，依据第四强度理论，判断优化的上壳体是否符合要求，此次研究的电池箱上壳体在非平整、急转弯、紧急制动极限工况下的具体工况要求如表3所示。

表3 工况要求

3.2 强度分析理论

在材料力学第四强度理论中，当材料的所受到的力破坏材料保持原有形状，并且不能恢复原有的形状，材料即会发生屈服[9]，即：

Uf≥Uv

(1)

式(1)中：

(2)

单向拉伸时，σ1=σ，σ2=σ3=0，此时形状改变能密度如式(3)所示。

(3)

将式(2)，式(3)代入到式(1)中化简后，破坏准则可表示为：

(4)

考虑到材料的安全系数n，结构性能安全的评价标准如式(5)所示。

(5)

式(5)中：n为安全系数，σs为材料的屈服强度，[σ]为安全系数下的许用应力[8-9]。

3.3 强度分析结果

采用CATIA有限元分析模块，第一种工况下的应力云图如图5所示，上壳体的最大等效应力为5.07MPa，位于T字形衔接部位，电池包上板折弯而成，衔接的部分特征尺寸不同，容易引起应力集中，局部的受力会超出上壳体材料的许用应力。

图5 非平整工况下的箱体应力云图

第二种工况和第三种工况的应力云图如图6所示，紧急转向工况下的最大应力为3.4MPa，位于T折弯部位，与非平整工况相比，该处的应力同样受力最大，容易引起应力集中，结构优化过程中，重视位于T折弯部位的强度大小，验证是否超出最大的许用应力，紧急制动工况的最大应力为2.6MPa，位置为上壳体顶端周围，应力在可控区间内，不会引起破坏，符合强度理论的要求。

(a)紧急转向情况

4 可靠性评估

本文采用模态及安全系数，分析上壳体的可靠性，主要考察结构的共振特性，上壳体与非平整路面受到的激励不能错开时，电池会因共振而发生更为严重的破坏，安全系数较小时，会产生强度破坏，所以需要增加结构刚度，提高固有频率，优化结构参数，提高电池包的整体性能。

4.1 模态分析理论

离散系统的振动微分方程为：

[M]{X″(t)}+[C]{X′(t)}+[K]{X(t)}

={F(t)}

(6)

式(6)中，[M]为振动系统的质量矩阵；[C]为振动系统的阻尼矩阵；[K]为振动系统的刚度矩；X(t)代表移动的位移；X′(t)代表移动的速度；X″(t)代表移动的加速度；F(t)为随时间变化的载荷激励向量[8]。

自由响应的振动系统可简化为：

[M]{X″(t)}+[K]{X′(t)}=0

(7)

位移函数采用正弦函数表示：

{X(t)}={A}sin(wt)

(8)

式(8)中，A为振幅列向量矩阵；ω为固有频率作为特征值问题，该方程亦可简化为：

([K]-ω2[M]){A}={0}

(9)

在无阻尼系统中，结构振幅{A}不全为零，可求得无阻尼自由振动频率方程：

([K]-ω2[M])=0

(10)

公式(10)即为无阻尼振动系统的特征方程。

若刚度矩阵和质量矩阵是实对阵正定矩阵，则求得的特征值数量与矩阵的阶次n相等，即有表示n阶模态的固有频率[10-11]。

4.2 电池包结构模态分析

电池包上壳体的振动是影响电池包的性能之一，模态结果表明该上壳体可有效分析共振，采用CATIA有限元分析模块电池包上壳体前十阶固有频率，如图7所示。

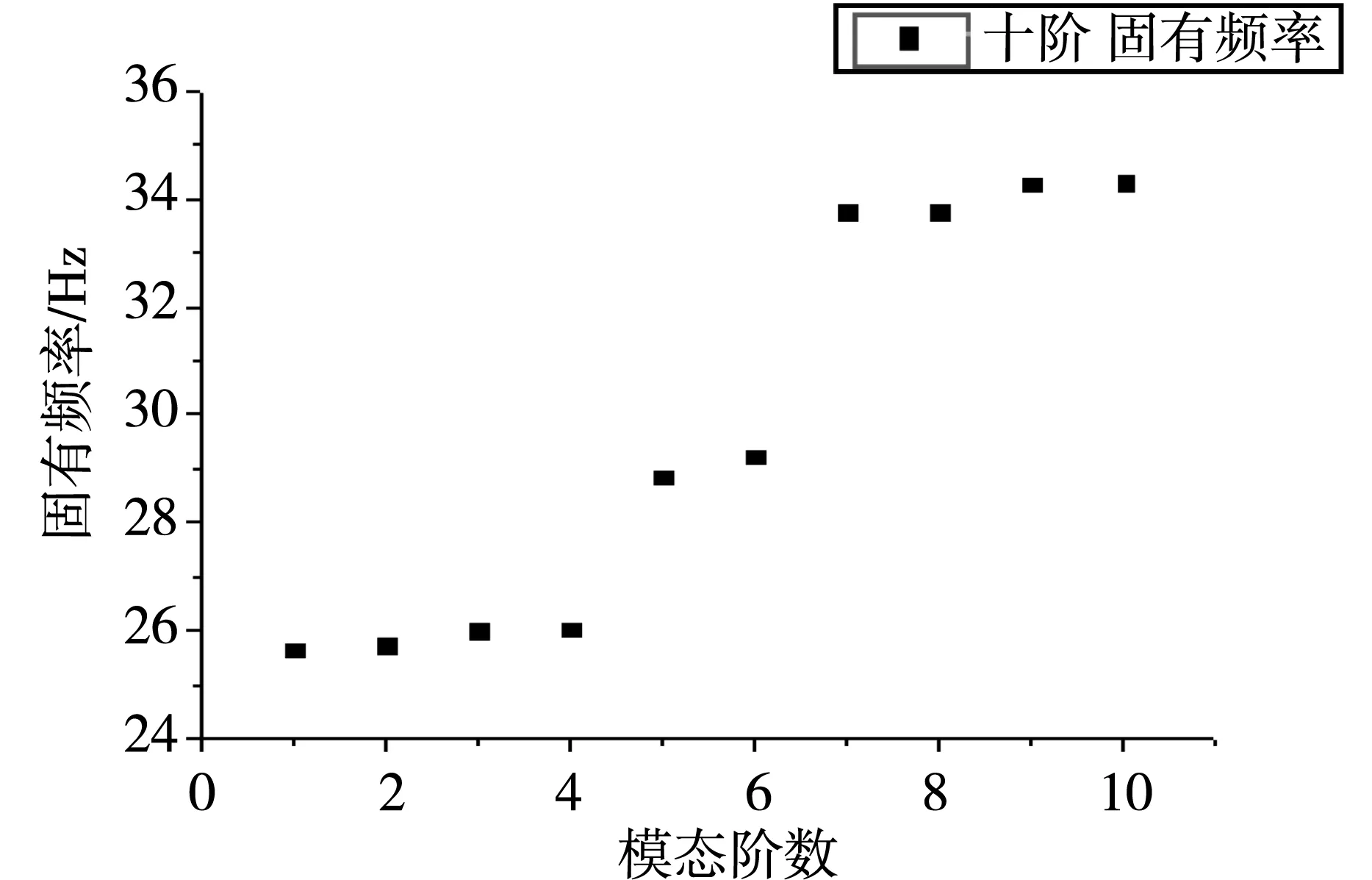
图7 电池包上壳体前十阶固有频率

激振源频率可接受的区间是15±5Hz，悬架的可接受的模态频率在20±10Hz，为了保证安全，上壳体与非平整路面解耦频率保持一定的差值[11]，才能减少上壳体的激励。为了安全起见，要求电池箱体的一阶固有频率大于33Hz，采用CATIA有限元分析模块计算，图7为计算的六阶振型，结果表明：前六阶均小于33Hz，未达到企业设计的要求，需要优化结构参数，根据图8可知：上壳体后四阶的固有频率均符合设计要求。

(a)电池包上壳体第1阶模态云图

4.3 电池包上壳体安全系数评估

安全系数是判断材料属性的重要指标之一，通过计算理论安全系数与标准安全系数进行对比，可进一步判断电池包上壳体的安全性，电池包上壳体静态有限元分析的安全系数可表示为：

(11)

式(11)中，σs为材料的屈服强度，n为安全系数；σmax各工况下的最大应力，当n≤1时，材料的强度属性就会被破坏，当安全系数n>1时，材料的强度属性处于安全的范围，结合强度分析结果可知，电池包上壳体安全系数处于大于1，处于安全的范围内[12]。

5 电池包上壳体优化

电池包上壳体在刚度未达到初步设计的要求，无法满足常规的设计要求，存在极大的共振现象。结合传统设计经验可知，动刚度只需提高上壳体的局部参数即可，具有较好的工艺性，制造技术上也较为成熟。

采用CATIA有限元分析模块的结果表明，本文电池包上壳体的低阶固有频率未符合企业设计要求，可采用模拟分析的结果，优化电池包上壳体的方式，提高固有频率，使结构的刚度满足设计要求。根据电池箱上壳体的设计情况，可选用两种优化方式，虚拟计算其结果是否满足要求，如图9和10所示。

第一种采用上壳体局部区域进行加厚，计算结构固有频率。

第二种布筋方式是根据其形貌特征用局部加强筋的方式增加其固有频率来达到电池包结构优化效果。

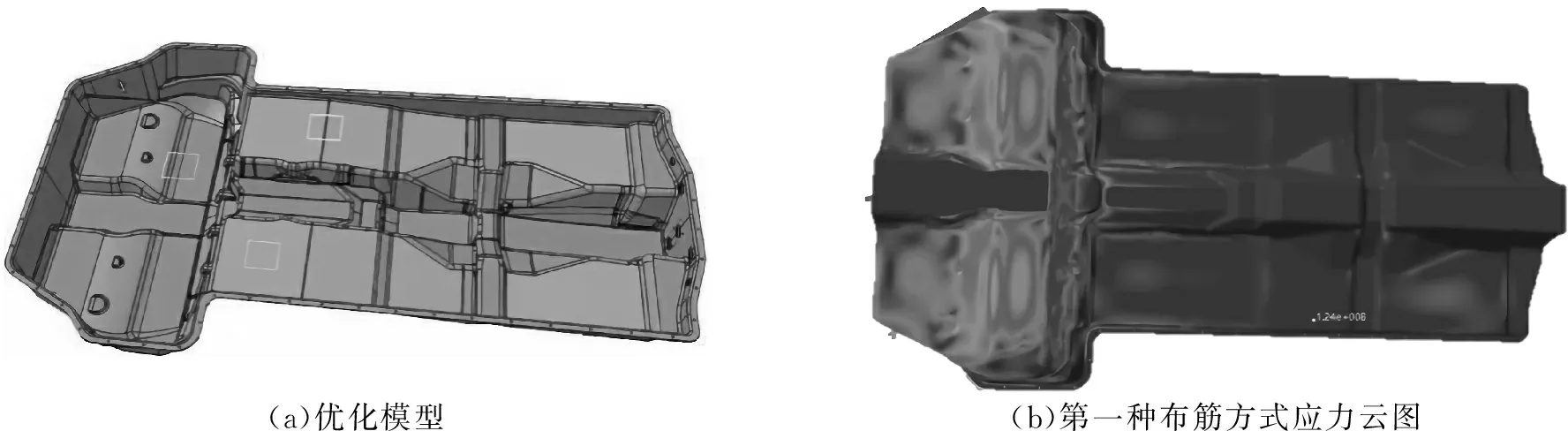
(a)优化模型(b)第一种布筋方式应力云图

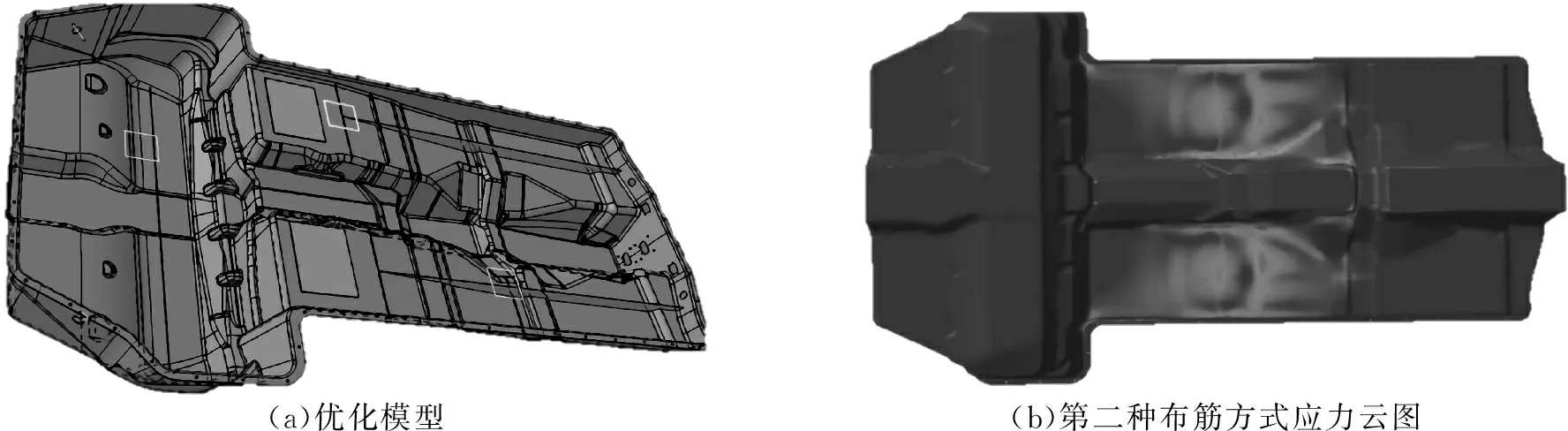
(a)优化模型(b)第二种布筋方式应力云图

由图9图、图10可知，两种优化方式均达到目标优化效果。第一种优化方式实际加工相对简单，加工精度低减小加工成本，第二种相比于第一种布筋方式较为复杂但是减少了使用材料，可根据实际情况择优选择，上壳体质量的变化如表4所示。

表4 优化前后的箱体质量对比

对优化后的电池箱体进行模态分析，固有频率曲线如图11所示，最下方曲线代表优化前方案，中间曲线代表第二种布筋方式方案，最上方曲线代表第一种布筋方式方案，优化的结果均大于初步设计的方案，安全系数满足要求，符合上壳体的初步设计要求。

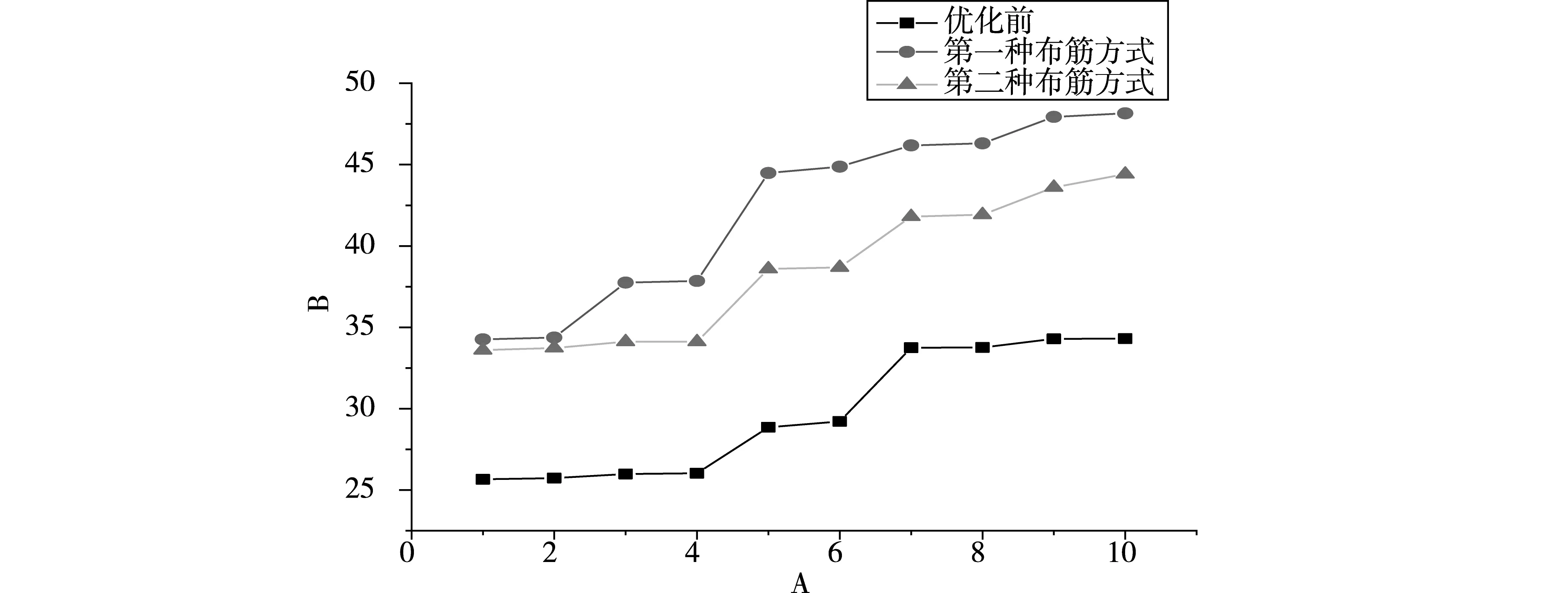
图11 优化前后的箱体固有频率对比

6 结论

采用有限元方法模拟计算电池包上壳体，评估了上壳体可靠性，提供了结构优化的方案，根据有限元分析及可靠性评估的结果，结论如下。

(1)在零件上平面，前平面，侧面施加三种方式的载荷测得的刚度值均满足安全系数大于1，刚度性能满足要求。

(2)从上下非平整，紧急制动，紧急转往三个典型工况分析了电池包的结构强度，最大效应力均小于材料的屈服强度，强度性能满足要求。

(3)初步设计的上第一阶的固有频率分别为25.66Hz，易发生共振现象。

(4)第一种优化后的电池包上壳体前二阶固有频率为34.26Hz和34.37Hz，较之前结构频率分别提升了33.5%和33.5%。第二种优化后的电池包上壳体前二阶固有频率分别为33.60Hz和33.73Hz，较之前结构频率分别提升了30.9%和31.1%。