曲柄滑块式折叠翼机构设计与仿真分析

吴文锦，郭高智，周昌兰，王煜瑄，朱永强

(青岛理工大学 机械与汽车工程学院，山东 青岛 266520)

在自然界，鸟类和昆虫在停止飞行时都能够将翅膀收缩，完全贴附在身体上，在飞行时，同样能够将翅膀完全展开，这种能够大幅度折叠和展开的机理使得鸟类和昆虫最大程度的发挥翅膀的性能，大幅展开有利于提高鸟类的飞行的能力，大幅折叠能够最大程度上保护翅膀不受伤害。因此，折叠翼飞行器具有良好的机翼折叠效果，进而越来越成为研究热点。

目前，关于折叠翼飞行器的折叠方式主要分为驱动方式折叠、主动被动折叠和刚性柔性材料折叠方式等，这些驱动方式存在折叠幅度小、可控性差和缺乏连续性的缺点[1-4]。为此，通过研究曲柄滑块机构，设计一种基于曲柄滑块式折叠翼飞行器。曲柄滑块机构与单曲柄双摇杆机构较为相似，单曲柄双摇杆机构在运动时，机构的非对称性导致左右两根杆件转动角度存在较大偏差，不利于机构稳定转动[5-7]。而曲柄滑块机构通过添加一个滑块和连接滑块与曲柄的连杆，解决了曲柄转动时机构左右不对称的问题[8]。曲柄滑块机构经过优化后，得到一种空间斜曲柄滑块机构，进一步保证了机构的对称性运动[9]。但是传统的单曲柄滑块双摇杆机构曲柄转动一个周期，摇杆转动角度较小，达到不到机翼折叠/展开幅度的要求。因此，本文在曲柄滑块机构的基础上加上摇杆，并进行改进，使得单曲柄滑块双摇杆折叠翼机构能够进行大幅度的折叠/展开运动。通过舵机驱动曲柄顺时针转动，即可完成机翼折叠动作，对机构进行运动学分析，并计算出合理的杆件长度，满足机翼折叠/展开需求。

1 折叠翼机构模型建立

曲柄滑块机构由于结构简单和机构的对称性，多被运用于扑动机构上，如图1所示。曲柄OC在电机的驱动下通过连杆BC拉动滑块B沿着滑槽运动，滑块B通过连杆AB、A1B拉动摇杆AO1、A1O2绕铰接点O1、O2上下扑动。根据曲柄滑块机构能够改变摇杆转动角度这一特性，将摇杆作为机翼折叠杆件，改变铰接点O1、O2和A、A1的位置，使得折叠杆能够围绕固定铰接点O1、O2转动，改进后的曲柄滑块折叠机构如图2所示。曲柄OC顺时针转动180°，通过传动杆BC驱动滑块B前后移动，滑块B通过拉杆AB、A1B将滑块的位移量转换成角度传递给机翼折叠杆，驱动机翼折叠杆AO1、A1O2绕固定铰接点O1、O2转动，以此完成机翼折叠和展开运动。

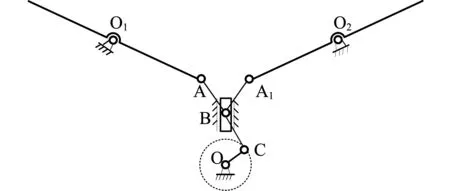
图1 曲柄滑块机构

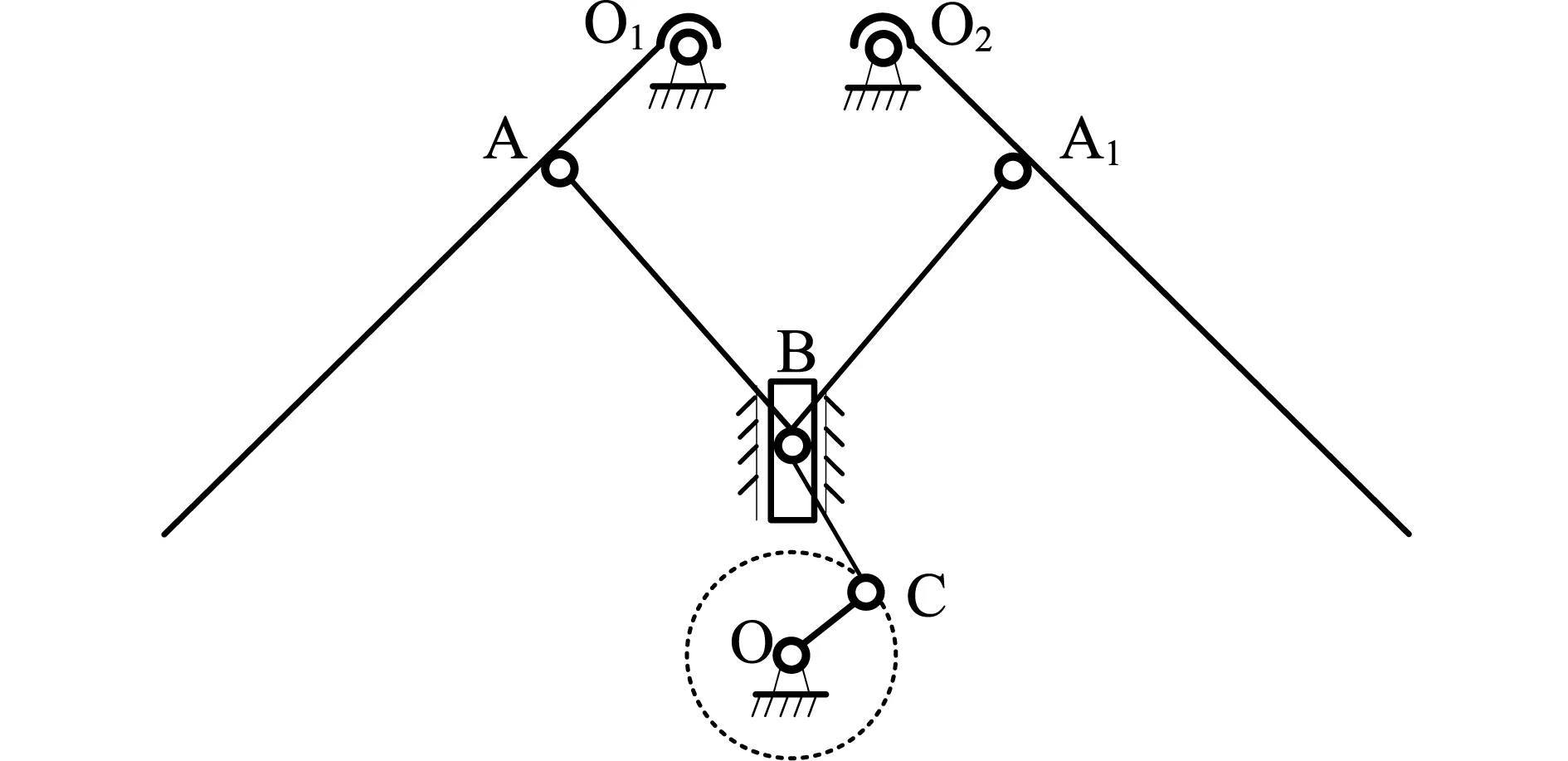
图2 改进后的曲柄滑块折叠机构

折叠翼机构设计旨在模仿鸟类翅膀大幅度的折叠和展开，对各杆件长度进行合理设计，使得曲柄顺时针转动180°，机翼折叠角转动幅度能够达到90°。另外，两侧拉杆的设计使机翼在大幅度转动过程中能够保持对称运动。

2 折叠翼机构运动学分析

2.1 运动学分析

由于机翼折叠杆和拉杆部分为对称结构，为便于研究取右侧部分加上曲柄滑块机构作为运动学分析的研究对象，如图3所示。其中曲柄OC的长度为l，传动杆BC的长度为l1，拉杆A1B的长度为l2，折叠杆A1O2部分的长度为l3；折叠杆固定铰接点O2距离机构中心线的距离为m，滑块B距离上端的长度设为s2，距离曲柄旋转中心的距离设为s1，s为二者的距离相加值；曲柄转动角度为θ，机翼折叠/展开角度为φ，α为拉杆与折叠角之间的夹角，β为曲柄与传动杆间的夹角，γ为辅助角。

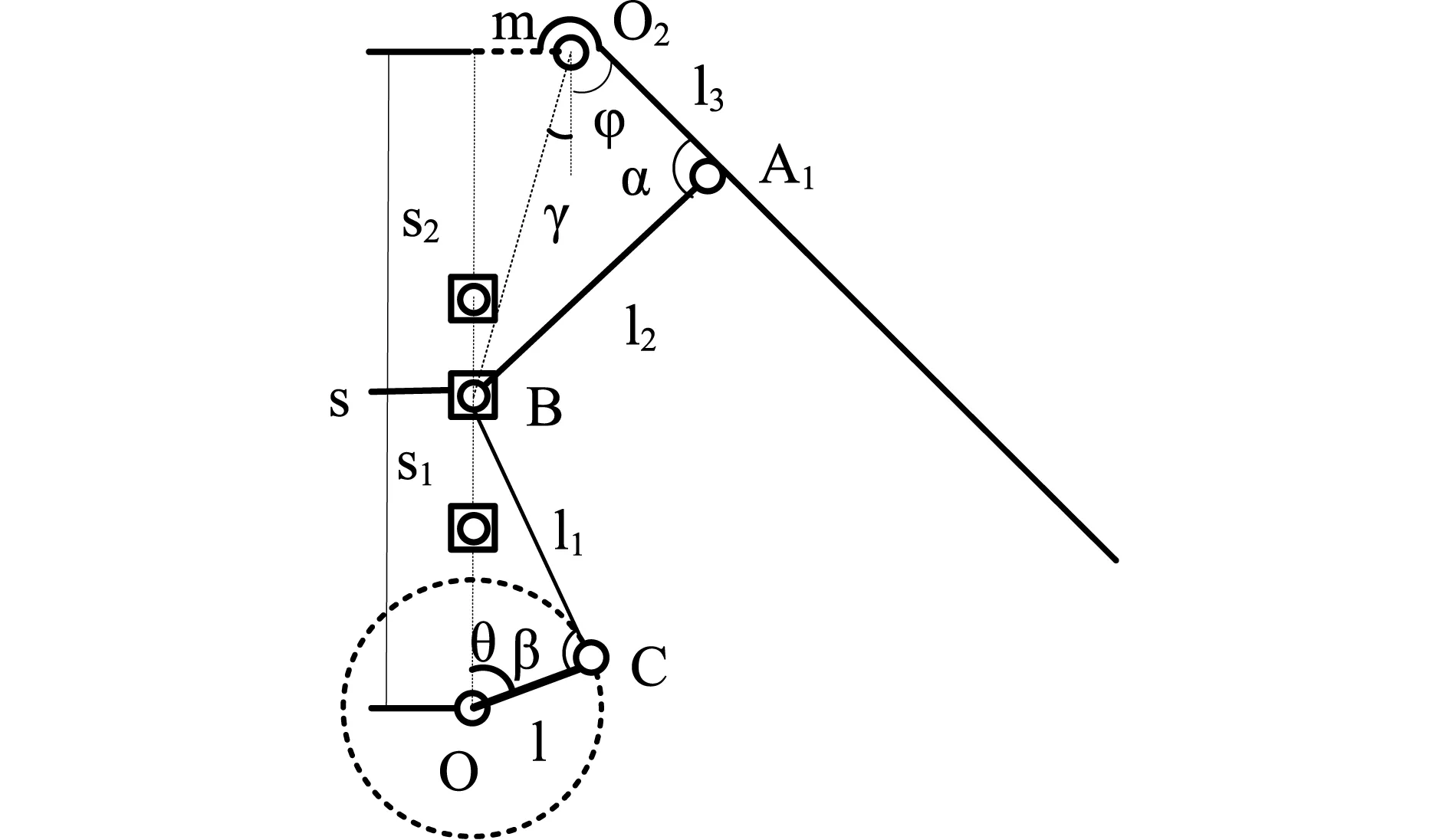
图3 曲柄滑块折叠翼机构

由图3可得曲柄转动角度θ计算公式如公式(1)所示。

(1)

化简可得以s1为未知数的一元二次方程如公式(2)所示。

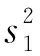
(2)

对公式(2)进行求解，由于设计模型中s1>0，故s1的值为：

(3)

由图3可得折叠杆与固定铰接点O2和滑块B连接线间的夹角计算公式为：

(4)

根据机构运动原理可以得出拉杆与折叠杆间夹角α和曲柄与传动杆夹角β为：

(5)

辅助角γ和BO2计算公式为：

(6)

将公式(6)代入公式(4)中可得折叠角φ：

(7)

由于s=s1+s2，则由公式(3)可得s2：

(8)

将公式(8)代入公式(7)得折叠/展开角φ为：

(9)

其中A、B和C的值为：

(10)

根据公式(9)可以看出折叠翼角度φ的大小除了受到曲柄转动角度θ的影响，还受到机构各杆件参数l、l1、l2、l3和s、m的影响，其中参数s和m影响机构杆件的长度，进而影响机构的稳定性和合理性。直接根据公式(9)进行模型设计，会因为结构参数较多和折叠翼机构折叠/展开幅度要求的问题，造成设计的机构参数达不到理想的结构尺寸参数和折叠翼折叠/展开幅度角度的要求，需要重新确定曲柄滑块折叠翼机构各杆件参数值。

2.2 机构参数选定

2.2.1 机构影响因素

设计参数选取曲柄长度l、传动杆长度l1、拉杆长度l2、折叠杆A1O2段长度l3、固定铰接点O2到结构中心线的距离m和曲柄中心点O至固定铰接点O2的垂直距离s为曲柄滑块折叠翼机构优化设计参数。

2.2.2 约束条件

曲柄滑块折叠机构在运动过程中为非对称结构，为了减小非对称性运动对折叠翼飞行器在空中滑翔飞行和折叠翅膀的影响，机翼展开和折叠时机构整体需为对称结构，则曲柄转动角度θ的运动范围设定为：0≤θ≤180°。

其他机械学条件：

曲柄长度：5mm≤l≤7mm；

曲柄约束条件：l+l1≤l2+l3；

传动杆长度：9mm≤l1≤12mm；

拉杆长度：15mm≤l2≤20mm；

折叠杆A1O2段长度：6mm≤l3≤9mm；

固定铰接点O2到结构中心线的距离m和曲柄中心点O至固定铰接点O2的垂直距离s的存在条件为s≤l1+l2。

2.2.3 优化目标

将机翼折叠幅度最大化是曲柄滑块折叠翼机构设计目标，折叠角φ的运动范围为：0≤φ≤90°，确定各杆件长度。

2.2.4 确定机构杆长参数

在曲柄滑块折叠翼机构设计时，机构各杆件长度初始值如表1所示。经过分析后，如图5黑色曲线所示，折叠最小角φ为4.74°，最大角度为92.52°，并不符合设计目标要求，为此需重新确定各杆件长度。

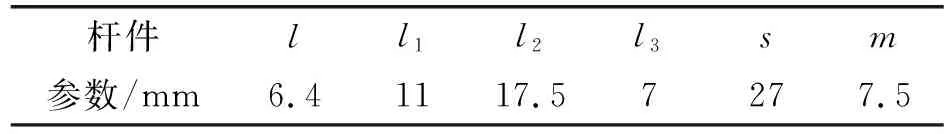
表1 机构各杆件初始值

曲柄长度越长，所需要的力矩越小；反之，所需力矩越大。为使机构更加合理和便于研究，曲柄长度取定值，为6.4mm，设定折叠角度幅度为φ=90°，计算出合理的杆件长度，如表2所示。

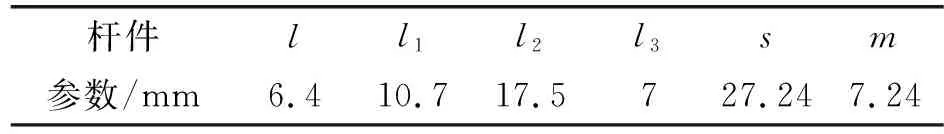
表2 机构各杆件优化值

将表1、2的参数代入公式(9)，利用MATLAB求解并绘制出优化前优化后的机翼折叠角φ随曲柄驱动角度θ运动关系曲线图，如图4所示，曲柄旋转180°，折叠翼机构由展开转变为折叠状态。优化前折叠角φ最大为88.2°，最小为5.18°，折叠/展开幅度为83.02°；优化后φ最大为90.26°，最小为-0.14°，折叠/展开幅度为90.4°，由于计算出的杆件长度取小数点后两位，故得到的φ角度上下存有极小的余量，在合理的范围之内，达到折叠展开幅度的设计要求。

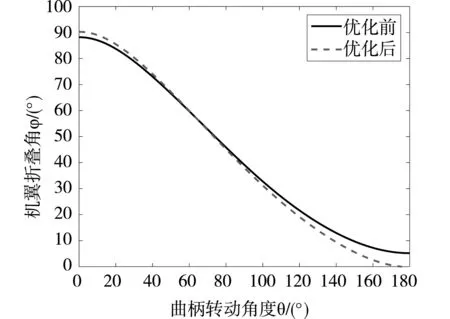
图4 优化前后机翼折叠角变化对比

将表2中的数据代入公式(5)，利于MATLAB进行求解并绘制曲线，得到曲柄与传动杆之间的夹角β和拉杆与折叠杆夹角α与曲柄转动角θ的运动变化曲线，如图5所示。曲柄转动一次角度为180°，曲柄与传动杆夹角β最小值为0°，最大值为180°，转动幅度达到180°，符合折叠翼机构设计要求；拉杆与折叠杆夹角α最小值为35.28°，最大值为155.8°，运动幅度为120.52°。

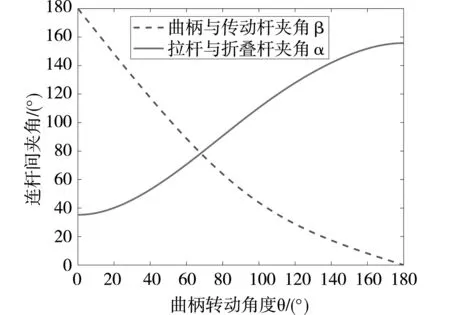
图5 折叠翼机构相关杆件间夹角关系变化曲线

3 ADAMS仿真验证

从理论分析来看，曲柄滑块式折叠翼机构能够符合扑翼机折叠要求，为验证其合理性，利用SolidWorks绘制的折叠翼机构模型，导出为“X_T”文件格式，再将“X_T”文件导入动力学仿真ADAMS中，如图6所示。在各杆件关节处添加旋转副，在滑块处添加移动副，移动副位置分别选定滑块和地面，运动副添加完毕后，在曲柄中心处的旋转副上添加旋转副驱动，将仿真时间设置为3s，定义运行时间函数为60.0d*time，仿真运行一次，曲柄转动180°，然后进行仿真验证。通过建立参考点，测量折叠杆输出的角度。在ADAMS后处理中查看输出角度曲线，并与理论分析进行比较，得到图7所示的曲线。

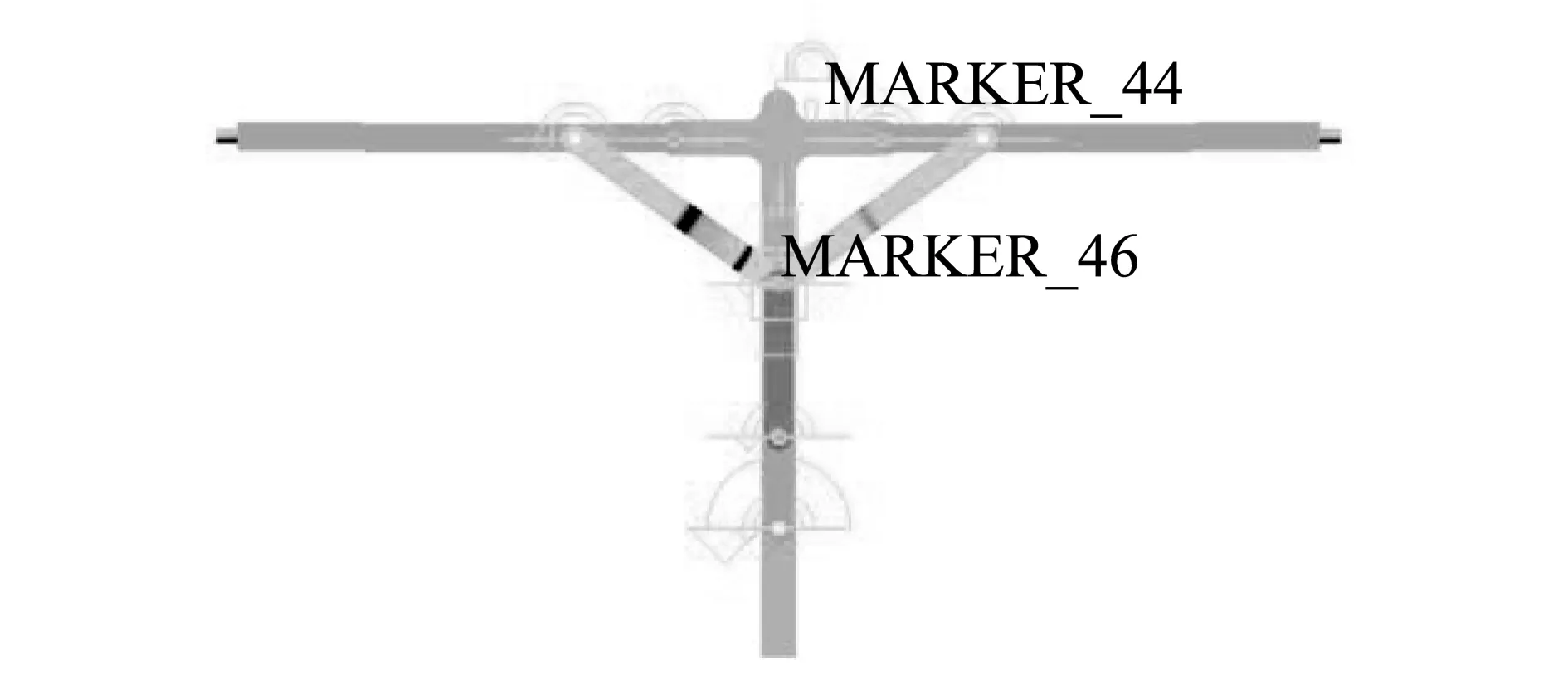
图6 ADAMS仿真

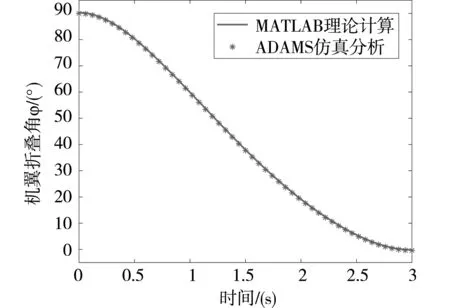
图7 理论计算与ADAMS仿真对比

如图7所示，MATLAB理论计算的折叠角度φ运动曲线与仿真分析得到的运动曲线完全一致，证明了理论分析正确，曲柄滑块式折叠机构设计具有合理性。

折叠翼飞行器机翼折叠角速度如图8所示，当仿真运行时间为0s时，角速度为0rad/s，当运行时间到1.14s时，角速度持续增加达到最大值为44.5rad/s，当运行时间到3s时，角速度持续较小直至为0rad/s。可以看出，折叠翼机构在机翼折叠过程中不会出现失速，具有良好的传动性。

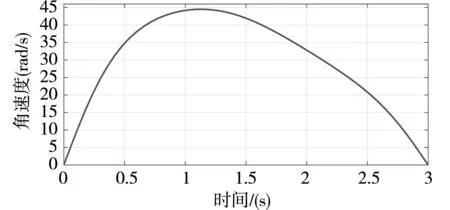
图8 曲柄滑块折叠机构折叠角速度仿真结果

4 曲柄滑块式折叠翼飞行器总体设计

利用三维建模软件SolidWorks建立曲柄滑块式折叠翼飞行器模型，如图9所示。

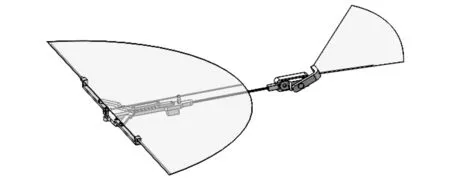
图9 曲柄滑块折叠翼扑翼机总体设计

折叠翼机构不同于扑动机构，折叠和展开为非持续性往复动作，因此，采用伺服舵机作为驱动机构较为合适。尾翼同样采用私服舵机作为驱动机构，能够上下扑动，维持折叠翼飞行器飞行姿态。图10为折叠翼飞行器在机翼折叠角φ=90°、φ=50、φ=0时的整体姿态，可以看出折叠翼飞行器能够由完全展开状态的90°折叠收缩为0°，整个运动过程具有连续性和流畅性。

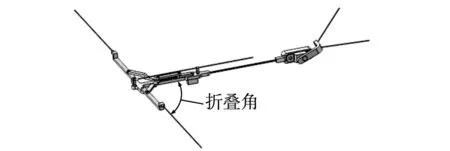
(a)φ=90°

5 结论

(1)基于曲柄滑块机构的基础上，将曲柄滑块机构的两根摇杆改变为两根机翼折叠杆，折叠杆对向的一段用铰接点固定，两根拉杆连接折叠杆和滑块，组成机构的折叠部分。改进的曲柄滑块机构应用于折叠翼机构具有良好的对称性和稳定性。

(2)依据改进的曲柄滑块折叠翼机构，进行运动学分析，并计算得到最优的机构杆件参数。利用MATLAB进行理论分析，曲柄转动180°，机翼完成一次折叠收缩动作，且机翼折叠幅度能够达到90.4°，达到预期的设计要求。利用ADAMS进行仿真分析，模拟机翼折叠运动姿态，并与理论分析进行比较，结果表明，理论分析与仿真结果一致，证明了理论的正确性。

(3)曲柄滑块式折叠翼机构在理论上具有可行性，为进一步验证理论的合理性，还需要进行实物制作和试验飞行，继续完善折叠翼飞行器的研究。