含软弱夹层岩体的剪切变形及破坏机理研究

顾 问， 丁 伟， 施 威， 王 金

（1.江苏省地质矿产局第一地质大队，南京 210041； 2.河海大学地球科学与工程学院，南京 211100）

在漫长的地质时期内，岩体因受到构造应力和各种物理化学作用的影响，在其内部形成了大量的节理、层理等结构面，软弱夹层就是其中一种力学性质比较特殊的结构面. 软弱夹层具有低强度、低弹性模量、高泊松比等特征，是边坡设计、地下开挖、坝基修建等工程活动中典型的不良地质，也是影响岩体稳定性的主要因素［1-4］. 近年来，由软弱夹层引起的隧道围岩垮塌、边坡滑动、坝基失稳等工程灾害时有发生，严重影响到人民的生命财产安全［5-7］.

目前关于软弱夹层对岩体力学特性及破坏机理影响的研究已有许多，且大多研究都是采用室内直剪试验、三轴压缩实验、环剪试验等手段进行的［8］. 赵宏刚等［9］通过真三轴试验研究了含软弱夹层的复合岩样在不同正压力条件下的力学响应和破坏特征. 许飞等［10］通过剪切试验研究了不同含水量以及不同厚度的软弱夹层的抗剪强度参数特性. 丁恩理等［11］通过室内三轴试验研究了不同夹层倾角、不同夹层厚度比对含薄层硬岩的软弱夹层试样的强度及破坏形式的影响. 傅旭东等［12］通过三轴固结不排水剪试验分析了含不同倾角的软弱夹层三轴试样的强度和破坏模式. 焦兵等［13］采用单轴压缩试验研究了不同倾角软弱夹层对砂岩强度和变形的影响. 王宇等［14］通过不同正应力水平下的剪切蠕变试验研究了软弱夹层的蠕变变形特征、破裂机制及其长期抗剪强度的确定方法.

数值模拟方法也是研究岩体力学性质和变形特征的有效手段之一［15］. 颗粒流是一种基于离散单元法的数值分析方法. PFC2D是一种广泛用于模拟岩体材料微观力学响应的离散元软件，通过该软件进行数值模拟能充分反映岩体材料的剪切力学性质. 随着科学技术的发展，越来越多的学者开始采用数值模拟的方法研究软弱夹层对岩体力学特性及破坏机理影响. 徐庆强等［16］采用颗粒流程序（PFC）建立了含不同软岩倾角和厚度比的双轴压缩数值试验模型，分析了倾角、厚度比及围压对含薄层硬岩的软弱夹层试样强度和破坏规律的影响. 张泽林等［17］通过三轴不排水剪试验和数值模拟方法研究了不同倾角软弱夹层试样的剪切力学特性及其剪切破坏特征. 张晓平等［18］采用PFC2D软件，通过数值模型试验对不同软弱夹层几何参数试样进行加载模拟，探讨了不同夹层厚度及不同倾角条件下试样的破坏过程和破坏形式. 范昊天等［19］以苏州市清明山关闭矿区矿山滑坡地质灾害为例，基于颗粒流程序对边坡失稳破坏过程进行了数值模拟，对含软弱夹层的顺层岩质边坡的变形破坏过程和滑移机理进行了分析和研究.

本研究在颗粒流程序中对不同结构面形态的含软弱夹层岩体试样进行数值模拟剪切试验，分析了粗糙度和法向应力对试样峰值强度以及残余强度的影响，并从微观角度分析了试样的起裂特征和裂纹扩展途径.

1 试样制备及试验设计

水泥砂浆具有与岩石相近的强度和破坏特征，被广泛用于制作节理直剪试样. 本研究将P.C32.5复合硅酸盐水泥、河砂和自来水按质量比为1∶3∶0.7的比例配制成硬岩，其单轴抗压强度为20.16 MPa. 为了确保相似材料的均匀性，采用筛网过滤细砂得到平均粒径为1 mm的干燥细砂颗粒. 为了减小试验结果的离散型，试验中软弱夹层采用石膏和水的混合物作为相似材料，经过反复配比，最终确定相似材料中水和石膏的质量比为0.4∶1.

利用3D打印技术制作锯齿状插片模板，其有效尺寸为150 mm×145 mm×5 mm（长×宽×高）. 插片模板的起伏角均为45°，起伏高度分别设置为5、10、15、20、25 mm. 采用预置裂隙法垂直插入插片，分别制备出5种不同壁面粗糙度的含软弱夹层岩体试样，试样尺寸均为150 mm×150 mm×150 mm（长×宽×高），插片模板起伏高度越高，其对应的试样壁面粗糙度越大. 每种级别粗糙度的试样均制作3个，共计15个试样. 采用S-h的命名方式对各组试样进行编号，其中h指插片模板的起伏高度，如起伏高度为5 mm的模板被编号为S-5.

试验遵循《工程岩体试验方法标准》［20］的规定，分别在1.0、2.0、3.0、4.0 MPa的法向应力和0.1 mm/s的剪切速度下用YZ-30B数显式剪切仪对15个试样进行直剪试验，试样剪切模型如图1所示.

图1 含软弱夹层岩体试样的制备过程及剪切模型Fig.1 Preparation process and shear model of rock mass specimen with weak interlayer

2 数值模拟微观参数的确定

使用PFC2D离散元软件建立数值模型. 通过数值模拟的方法来分析含软弱夹层岩体试样的剪切力学性质和变形特征. 通过反复试错，最终确定数值模型中各材料的微观参数取值（表1）. 试样上下盘以及软弱夹层内的颗粒之间使用平行黏结接触模型进行模拟，壁面处设置为光滑节理接触模型.

表1 数值模型中各材料的微观参数Tab.1 Microparameters of materials in the numerical model

峰值强度和残余强度是表征岩体强度特征的两个重要参数. 由表2可知，通过数值模拟试验得到的试样强度普遍比通过室内直剪试验得到的试样强度要小，推测是制备试样时压密不紧实、有瑕疵，或是试验过程中损伤裂纹破坏再平衡、试样的胶结变化等问题导致试样的峰值强度和残余强度增加. 但是总体而言，室内直剪试验和数值模拟试验得出的结果相差不大，两者之间差值比的绝对值均小于10%，说明所确定的数值模型中各材料的微观参数取值比较合理，微观参数取值能有效还原试样在室内直剪试验中的强度变化和变形特征.

峰值强度是衡量岩体试样抗剪切能力的重要指标，根据表2可知，试样的残余强度总小于其峰值强度，这是因为在直接剪切过程中，试样达到峰值强度时的黏聚力最大，一旦突破这一状态，试样的黏聚力会逐渐减小，当达到残余强度时，试样的黏聚力为0，即峰值强度需要克服岩体内部的黏聚力和由正应力引起的摩擦力，而残余强度仅需克服由正应力引起的摩擦力.

表2 室内直剪试验和数值模拟试验结果对比Tab.2 Results comparison of indoor direct shear test and numerical simulation test

3 结果与分析

3.1 粗糙度和法向应力对含软弱夹层岩体试样强度的影响

为了探究粗糙度对含软弱夹层岩体试样强度的影响，在不同法向应力作用下，通过数值模拟试验获得了5组不同粗糙度的含软弱夹层岩体试样的切向应力-切向位移曲线，如图2所示. 根据图2和表2可知，在1.0 MPa法向应力作用下，各组试样的切向应力峰值范围为1.1～2.9 MPa，其中S-5试样峰值强度为1.1 MPa，其余各组试样的峰值强度均大于1.8 MPa，且S-5试样的残余应力也明显小于其他组试样的残余应力，除了S-5试样外，其余各组试样的残余应力差异较小；在2.0 MPa法向应力作用下，各组试样的切向应力峰值范围为1.8～4.7 MPa，其中S-15试样比其他组试样更晚进入弹性阶段，各组试样的残余应力和峰值应力均随着试样粗糙度的增加而增大；在3.0 MPa法向应力作用下，各组试样的切向应力峰值范围为2.1～5.3 MPa，各组试样的残余应力和粗糙度呈正相关关系，即粗糙度越大的试样，其残余应力也越大；在4.0 MPa法向应力作用下，各组试样的切向应力峰值范围为1.3～5.7 MPa，其中S-25试样的起裂时间明显比其他组试样要早，各组试样的峰值应力和残余应力均与试样粗糙度呈正相关关系. 以上结果说明，岩体试样的峰值强度和残余强度均会随试样粗糙度和法向应力的增加而增大，分析原因可能是：对于不同壁面形态的岩体试样而言，随着壁面起伏高度的增加，壁面具备的摩擦系数也会随之增大，则岩体试样的峰值强度和残余强度均会随之增加；在不同法向应力作用下，试样所受的摩擦力会随着法向应力的增加而增大，因此试样的峰值强度和残余强度均会随着法向应力的增加而增加.

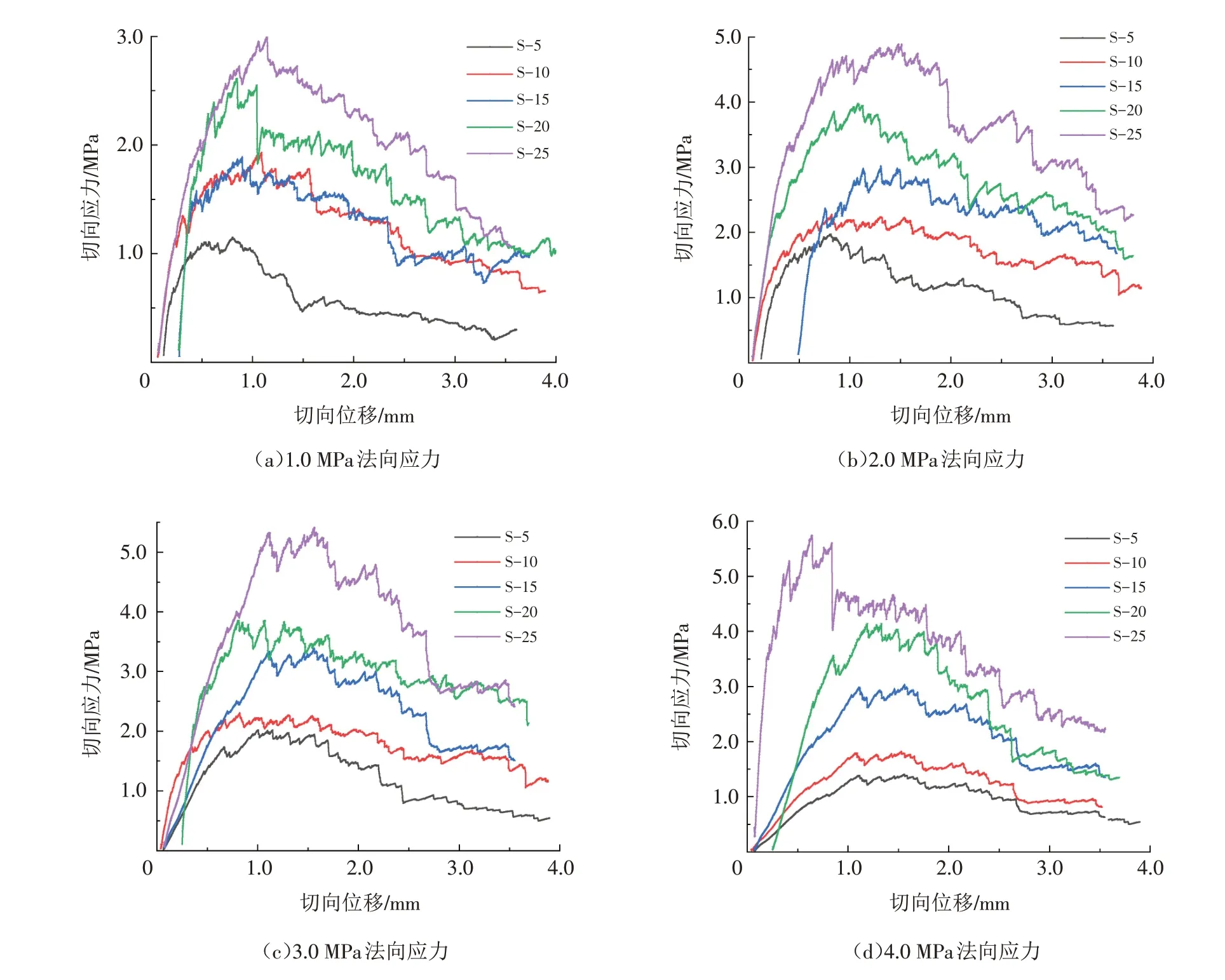
图2 不同法向应力作用下各组试样的切向应力-切向位移曲线Fig.2 Tangential stress-tangential displacement curve of each group of samples under different normal stresses

3.2 剪切变形微观响应特征

3.2.1 直剪试验微裂纹发育特征

图3为通过数值模拟试验得到的各组试样在2.0 MPa法向应力作用下的裂纹数量随切向位移的变化曲线. 从图3可以看出，当切向位移为0.4～0.6 mm时，多组试样出现张裂纹；当切向位移为1.0～1.4 mm时，多组试样出现剪裂纹，这说明含软弱夹层的岩体出现张裂纹和剪裂纹的时间并不完全一致，且剪裂纹出现的时刻稍迟于张裂纹出现的时刻. 同时，从图3可知，各组试样的剪裂纹数量远低于张裂纹数量，经统计，张裂纹数量占总裂纹数量的77.1%～92.4%，说明含软弱夹层岩体试样在剪切过程中，以受拉应力为主，剪应力仅存在于试样壁面和软弱夹层的尖端处，在尖端处应力容易集中从而产生剪切破坏. 试样S-5和试样S-10的张裂纹数量均在切向位移为1.5～2.5 mm之间突然增加，并且至破坏后不再增加；试样S-15分别在切向位移为1.4、2.7、3.5 mm处出现3个稳定阶段；试样S-20有3个稳定阶段，分别是在切向位移为1.4、2.9、3.3 mm处，且前2个增加阶段的持续时间均较短；试样S-25有4个稳定阶段，分别是在切向位移为1.5、3.0、3.5、4.3 mm处，且在1.5、3.0 mm处的增加阶段的持续时间均较短. 由此可知，试样的破坏阶段随着粗糙度的增大而逐渐增加，同时裂纹的数量也和粗糙度呈正相关关系，分析原因可能是，粗糙度增加了试样的接触面积和抗剪强度，使得切向应力对软弱夹层和壁面的作用更加明显.

图3 在2.0 MPa法向应力作用下各组试样的裂纹数量随切向位移的变化曲线Fig.3 Crack number change of each group of samples with the tangential displacement under the action of 2.0 MPa normal stress

根据数值模拟试验中裂纹的破坏过程可知，试样中较大的裂纹主要由众多微裂纹互相延伸贯通而成的. 通过观察不同时间步长下的试样形态发现，各组试样的破坏都是沿着最薄弱的软弱夹层开始产生裂纹，且主要以短小的裂纹为主，裂纹密集分布在结构面上、下盘凸起处和结构面中间的位置，从而会促使软弱夹层发生位移错断；各组试样的裂纹以张裂纹为主，剪裂纹数量非常少，且剪裂纹主要集中于壁面和软弱夹层相交的凸起尖端处.

3.2.2 接触应力分布特征

通过数值模拟方法研究了各组试样在2.0 MPa法向应力作用下破坏后的接触应力分布特征，结果如图4所示. 图中蓝色部分代表岩体间的接触应力，绿色部分代表软弱夹层之间的接触应力，红色部分代表岩体和软弱夹层接触部分的接触应力，图中线的粗细代表接触应力的大小.

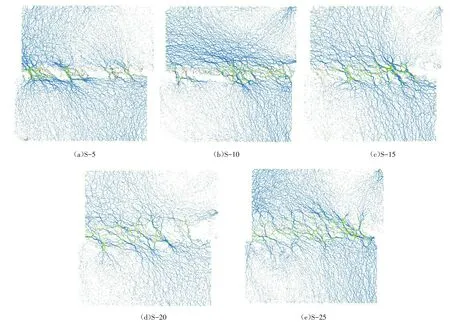
图4 各组试样在2.0 MPa法向应力作用下破坏后的接触应力分布特征Fig.4 Contact stress distribution characteristics of each group of samples under 2.0 MPa normal stress after failure

由图4可知，较粗的线条集中于软弱夹层和结构面附近，说明试样破坏后，接触应力分布于软弱夹层以及结构面和软弱夹层接触的部分，但也不是完全均匀分布，越向试样中部靠近的部分接触应力越密集，同时接触应力和切向应力的夹角都集中在30°～60°之间. 对不同粗糙度的试样而言，其接触应力的集中方式略有不同. 在切向应力的作用下，相同法向应力作用下的试样的接触应力偏转角度有很大的不同，随着粗糙度的逐渐增大，接触应力逐渐向法向应力的方向靠近，因为粗糙度是以起伏高度作为衡量标准的，所以粗糙度越大的试样，其壁面表面起伏的高度越高，则法向应力作用的路径就越长，从而使得接触应力最终向法向应力方向靠拢. 通过以上分析可推测，含软弱夹层岩体试样的裂纹起裂位置集中于试样的中部，并由试样的中部向试样的上下盘延伸，和接触应力的分布具有相似性.

3.2.3 颗粒移动特征

图5为试样S-5、S-10、S-15和S-20破坏后，其软弱夹层附近的颗粒位移矢量图，其中绿色部分为破坏后的软弱夹层颗粒，箭头为软弱夹层上、下两侧的位移矢量，箭头大小代表了位移的大小. 切向应力的初始方向规定为水平向右，试样破坏后可以观察到：软弱夹层附近的颗粒位移矢量发生轻微偏转，靠近结构面上盘一侧的颗粒位移矢量向右上方偏转，靠近结构面下盘一侧的颗粒位移矢量向左下方偏转；结构面上下盘处的颗粒位移矢量方向偏转较大且方向相反，这说明试样壁面上的颗粒在剪切过程是向相反方向运动的，会产生拉张的效应，从而导致试样在直剪试验过程中产生的主要是张裂纹.

图5 颗粒位移矢量图Fig.5 The vector diagram of particle displacement

从图5还可以看出，粗糙度较大的试样的颗粒位移矢量集中在远离软弱夹层的根部，而粗糙度较小的试样的颗粒位移矢量则集中在软弱夹层附近，这也从微观角度证明了在室内直剪试验中，粗糙度较大的试样主要发生啃断型破坏，粗糙度较小的试样主要发生磨蚀型破坏这个结论是合理的.

4 结论

利用颗粒流离散元软件PFC2D，通过数值模拟方法分析了不同粗糙度和不同法向应力对含软弱夹层岩体试样的强度和变形的影响，并从微观角度分析了试样的裂纹发育特征、接触应力分布特征、颗粒移动特征，得出结论如下：

1）试样的峰值强度和残余强度均随着试样粗糙度和法向应力的增加而增加，其中粗糙度对试样的峰值强度和残余强度的影响最大，法向应力次之，结构面壁面强度的影响最小.

2）试样微裂纹起裂的位置集中在软弱夹层和结构面相交的位置，尤其是在试样中部壁面的凸起位置处，该处是试样最薄弱的位置. 裂纹以张裂纹为主，剪裂纹数量较少.

3）粗糙度较小的试样以磨蚀型破坏为主，微裂纹难以发育成宏观裂纹；粗糙度较大的试样主要发生啃断型破坏. 试样的接触应力分布特征和颗粒移动特征均表明，试样的破坏受到法向应力的影响，法向应力越大，对试样的破坏作用越明显.