基于经验模态分解的CEEMDAN-FE-LSTM传染病预测

李顺勇， 何金莉

（山西大学数学科学学院，太原 030006）

传染病是由各类病原体引起的、可大范围传播且传播速度较快的疾病［1］. 甲乙类传染病中，肺结核、乙肝、布鲁氏菌病和艾滋病是每年发病人数较多的法定传染病. 若能掌握其发病规律，预测其发病趋势，并对发病状况进行分析与预测，可以为传染病防控工作提供科学的建议，对传染病防治具有重要的意义［2］.

近年来，随着人工智能发展，已有众多模型应用于传染病预测分析中. 徐映梅和陈尧［3］考虑对非结构化数据与单变量数据在模型预测上的效果差异，对比了自回归移动平均（Autoregressive Integrated Moving Average，ARIMA）模型与长短期记忆神经网络（Long Short-term Memory，LSTM）模型在国民生产总值季度数据上的预测效果. 冯一平等［4］对比了分布滞后线性模型（Distributed Lag Non-linear Model，DLNM）与LSTM 模型在预测山东省手足口病的发病趋势上的效果. 单一的预测模型通常具有一定的局限性，例如ARIMA模型在捕捉非线性关系上存在局限，DLNM对模型假设条件较敏感. 对此，赖晓蓥和钱俊［5］运用LSTM模型对ARIMA模型残差序列的非线性成分进行校正，用XGBoost集成预测模型，但其没有考虑到时间序列本身的复杂度，且没有挖掘时间序列中的潜在信息.

传染病数据常常具有非平稳、非线性的特征，而信号分解能够提取序列的局部特征且保证序列的平稳性，降低时间序列的复杂度，进而提升时间序列的可预测性［6-7］. 对此，本文提出了一种基于自适应噪声完备集合经验模态分解（Complete Ensemble Empirical Mode Decomposition with Adaptive Noise，CEEMDAN）和模糊熵（Fuzzy Entropy，FE）改进长短时记忆网络（LSTM）的传染病组合预测模型. 首先运用CEEMDAN 算法将序列分解；接着运用FE算法计算各分量复杂度并将其重构，以发掘序列的潜在信息，提高运算的效率；最后建立LSTM模型［8］对重构的序列进行预测. 本文采用RMSE、MAE和MAPE三种评价指标对预测效果进行评判，选取SARIMA、CEEMDAN-FE-SARIMA 和LSTM 作为对比模型. 从模型的预测效果上探索模型在传染病预测中的适用性，以期发现传染病发病的变化规律，为传染病预防控制提供依据.

1 背景知识

1.1 CEEMDAN

CEEMDAN［9-10］由经验模态分解（Empirical Mode Decomposition，EMD）发展而来，通过添加自适应的白噪声能使EMD中的模态混叠问题得到有效改善，改善后信号分解的重构误差极小. 该方法适用于将非线性和不平稳的信号分解成不同尺度的模态分量与残差分量，实现步骤如下.

步骤1对时间序列添加白噪声序列，并进行EMD分解取平均得到模态分量IMF1. 假设原始时间序列为x(n)，自适应系数为ε，对于每次分解都加入白噪声序列ωi(n)，则第i次添加噪声后的序列xi(n)为

EMD分解N次实验的均值为模态分量IMF1，即

步骤2计算步骤1得到的余量序列r1(n)，并由此计算IMF2，计算方法如式（3）和式（4）所示：

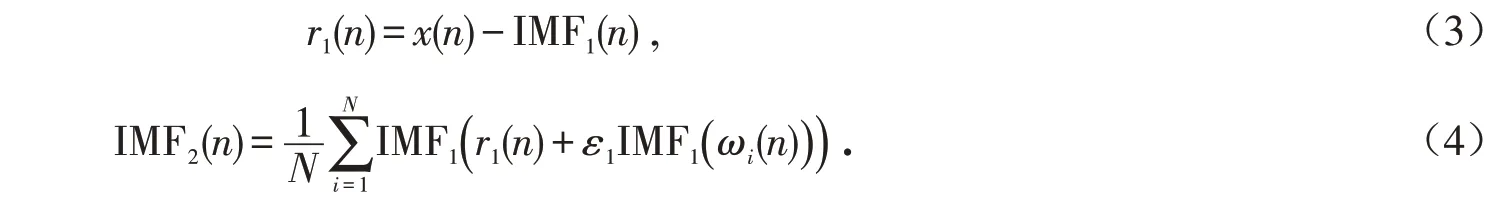
步骤3重复步骤2的计算至第k+1步，得到第k步的余量序列rk(n)以及第k+1个模态分量IMFk+1，即

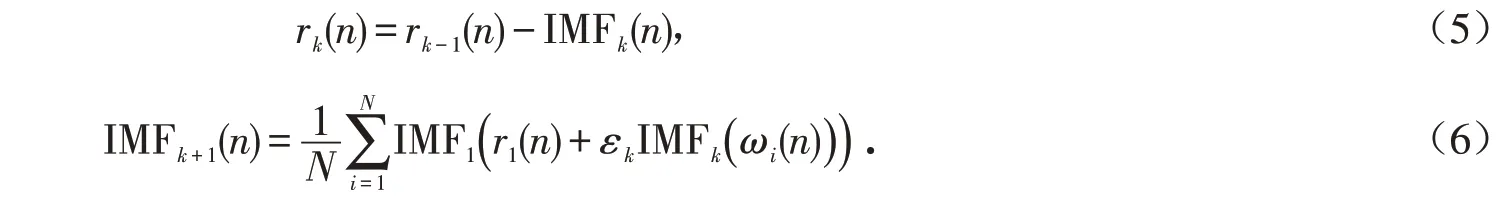
步骤4重复上述步骤，直至余量序列的极值点个数小于等于2时停止，得到固有模态分量IMFk以及残差序列RES，此时得到的时间序列为

1.2 FE

FE算法［11-12］是一种计算时间序列的复杂度与随机性的动力学方法. 与近似熵和样本熵不同，该算法通过指数函数来代替绝对幅值差，减小了数据波动对结果的影响，能使模糊熵值随着参数改变而平稳变化［13］，实现步骤如下.

1.3 LSTM

LSTM［14］作为一种特殊的循环神经网络，能有效解决循环网络中梯度消失与梯度爆炸问题，并且能够学习数据中长期的信息［15］. 该模型的内部包括了输入门、遗忘门和输出门，在遗忘门中该模型对上一步传递的信息进行有选择性的记忆与遗忘，实现了信息在隐藏态上更新. LSTM的内部结构如图1所示.

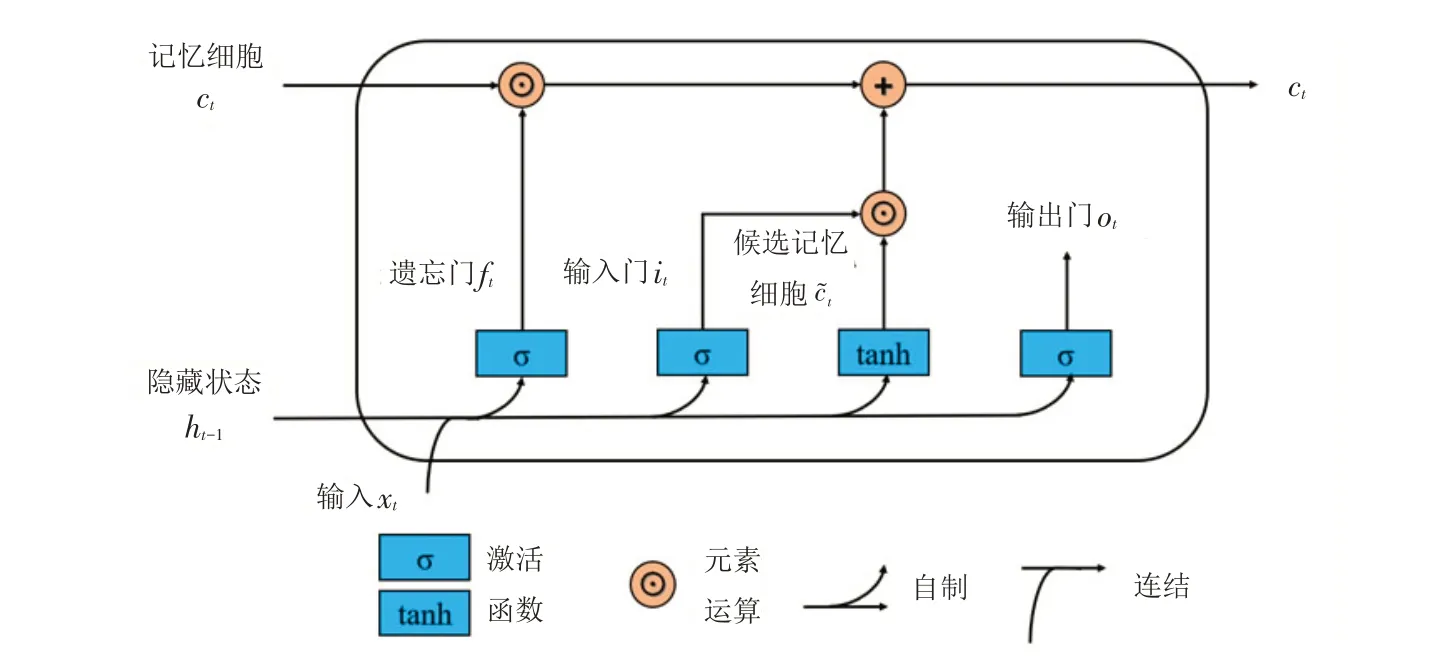
图1 LSTM的内部结构图Fig.1 Internal structure of LSTM

LSTM网络的计算公式如式（14）～（19）所示：

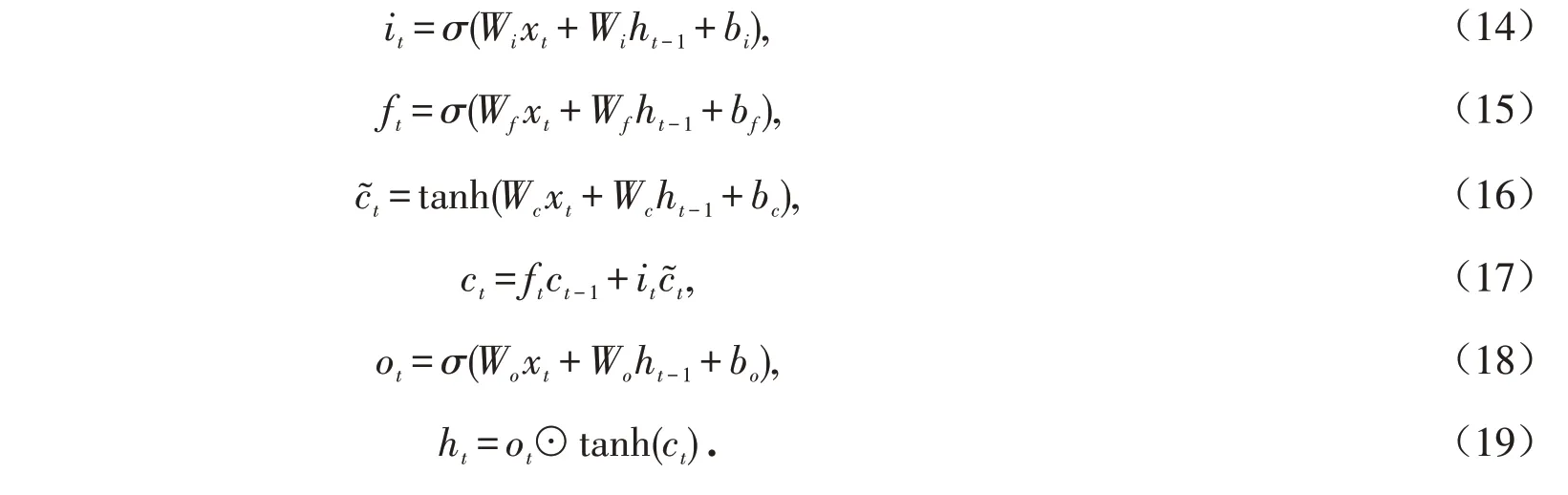
其中：xt表示当前时刻的输入；ht-1表示前一时刻隐藏层的输出；it、ft、ot分别表示输入门、遗忘门、输出门的值；W表示权重系数；表示当前时刻记忆单元输入的值；ct表示当前时刻记忆单元的更新值；σ、tanh 为激活函数.

2 CEEMDAN-FE-LSTM模型构建

传染病发病受到地理条件、气候条件等多种因素影响，发病人数呈现典型的非线性、非平稳趋势. 本文通过建立基于CEEMDAN-FE-LSTM的传染病预测模型，实现对传染病发病数据预测研究，具体步骤如下.

步骤1数据分解. 对传染病数据x(n)进行分解，由式（2）计算EMD 分解N次实验的均值作为第一个模态分量IMF1，并由式（3）计算得到余量序列r1(n). 对每次分解都加入白噪声ωi(n)，如式（4）～（7）所示. 当余量序列的极值点个数小于等于2 时停止，得到m个频率由高到低的模态分量IMF1，IMF2，…，IMFq以及残差分量RES.

步骤2不同尺度数据的重构. 对分解后的每个模态分量由式（8）～（10）计算空间向量和，计算两空间向量之间的切比雪夫距离和相似度以及在m和m+1维下的关系维度φm(n,r)和φm+1(n,r)，最后根据式（13）计算得到该分量的模糊熵. 重复上述步骤得到所有分量下的模糊熵FE1，FE2，…，FEq. 将FE值相差0.05以内的分量序列进行重组得到重构序列x1(n)，x2(n)，…，xk(n) . 其中k＜q.

步骤3重构数据的LSTM 预测. 将重组后的数据序列x1(n)，x2(n)，…，xk(n). 首先进行归一化处理以提高模型的运算效率和模型的预测精度. 然后将归一化后的序列分别建立LSTM模型进行预测，在隐藏层内由式（14）～（19）计算t时刻输入门、遗忘门、输出门的值分别为it、ft、ot，计算当前记忆单元的更新值ct和隐藏层的输出值ht，最后由输出层输出各序列的预测结果. 反归一化预测结果并进行累加，得到最终预测结果.

3 仿真实验结果分析

3.1 数据获取

本文选取的肺结核、乙肝、布鲁氏菌病和艾滋病月患病资料均来源于中华人民共和国国家卫生健康委员会（http：//www.nhc.gov.cn/wjw/index.shtml），数据范围为全国数据，数据周期为2010年1月至2021年12月.

3.2 评价指标选取

为比较不同模型在各患病数据集上的预测效果，采用RMSE、MAPE和MAE三个指标对模型预测精度进行评价，使用Python3.8.5软件进行仿真实验，指标计算公式如下式所示：

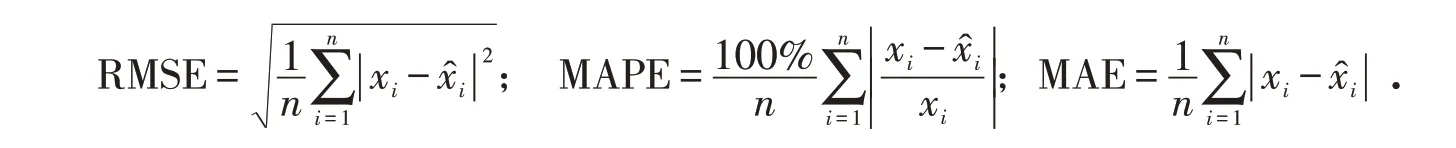
其中：x表示月发病数的实际值；表示模型的预测值；n为预测总月数. RMSE、MAPE和MAE量化了预测值与实际值之间的误差大小，该值越小说明模型效果越好.

3.3 CEEMDAN-FE分解与重组

首先，对四个疾病数据集进行CEEMDAN分解，如图2～图3所示. 可以看出，原始序列被分解为多个频率由高到低的IMF分量和1个残差分量，频率越低的IMF分量序列呈现出越平滑的趋势. 残差分量的量级约为10-7，分解误差很小，说明序列被完全分解.

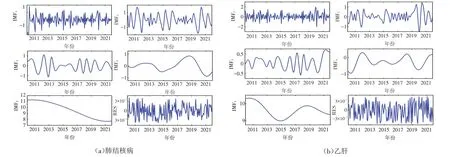
图2 肺结核病与乙肝数据集CEEMDAN分解序列图Fig.2 CEEMDAN decomposition of tuberculosis and hepatitis B dataset

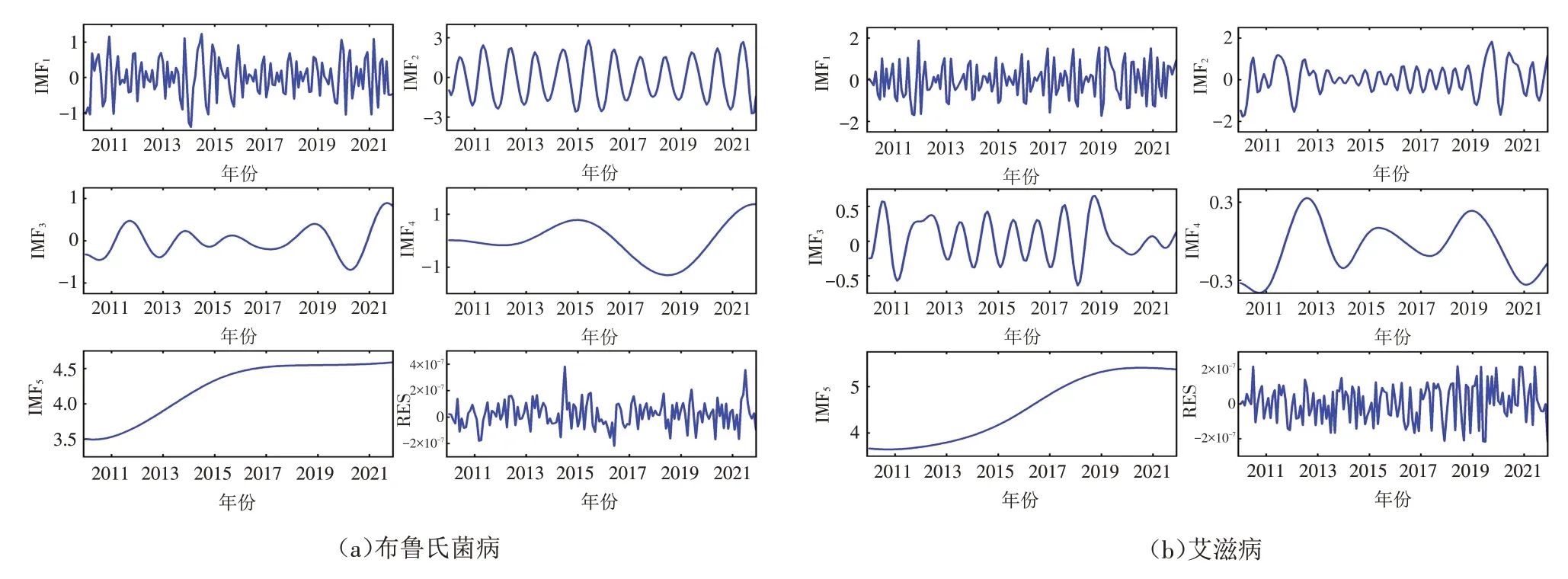
图3 布鲁氏菌病与艾滋病数据集CEEMDAN分解序列图Fig.3 CEEMDAN decomposition of brucellosis and AIDS dataset

为了更准确反映被分解序列的尺度，提升模型的预测精度，同时降低计算规模，因此对各分解后的序列计算FE值，得到各分解子序列的复杂度，如表1所示.

表1 各数据集上分解序列的FE值Tab.1 FE values of decomposed sequences on each dataset

由表1可以看出，在各数据集中分解的IMF分量的FE值随该分量频率的降低而越来越小，说明由高频分量至低频分量的序列随机性和复杂度逐渐降低. 通过比较FE值之间的接近程度对分解的各序列进行重组，将FE值相差0.05以内的分量进行合并得到重构的序列.

3.4 预测结果分析

对重构后的序列分别建立LSTM模型. 由于在LSTM神经网络中，隐藏层的个数以及对应神经元的个数对模型预测精度的影响较大［16-18］，经多次实验之后，本文设置2个隐藏层，每个隐藏层的神经元个数取32，拟合预测的时间步长设定为4，输出变量的个数为1，迭代次数为100次，并使用Adam函数优化内部参数. 采用SARIMA模型、CEEMDAN-FE-SARIMA模型和LSTM模型作为对比算法.

参数设置方面，对于SARIMA模型［19-20］和CEEMDAN-FE-SARIMA模型，经过分析自相关系数和偏自相关系数图，确定赤池信息准则（Akaike Information Criterion，AIC），准则的最小AIC值对应参数为p=1，q=1，d=1，P=1，D=1，Q=0. LSTM模型的具体参数与本文提出的模型参数相同.

模型预测结果如图4～图5 所示. 通过对比各数据集上的模型预测值与实际值曲线，可见CEEMDANFE-LSTM模型较单一的LSTM模型预测误差更小，预测值与实际值更为接近. 并且CEEMDAN-FE-SARIMA模型与SRIMA模型在数据前半段的预测值与实际观测值较接近，但在后半段数据上的预测误差均较大. 综合以上可知，基于CEEMDAN-FE-LSTM模型的预测结果较其他模型更好，虽然在部分拐点处与实际观测值有所偏差，但是总体预测误差较小，整体上更好地反映了传染病的发病趋势.

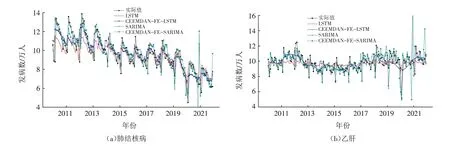
图4 肺结核病与乙肝数据集各模型预测效果Fig.4 Prediction effects of each model in the tuberculosis and hepatitis B dataset

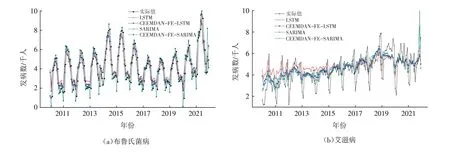
图5 布鲁氏菌病与艾滋病数据集各模型预测效果Fig.5 Prediction effect of each model in brucellosis and AIDS dataset

不同模型在RMSE、MAE和MAPE三个评价指标上的对比结果如表2和表3所示，各个指标上性能最优的算法用加粗表示. 由表2和表3可知，在肺结核病、乙肝、布鲁氏菌病和艾滋病四个数据集上，CEEMDANFE-LSTM模型较其他模型相比具有更小的RMSE、MAE和MAPE值，反映了该模型能更好地对非线性、非平稳的时间序列进行拟合与预测. 在乙肝数据集上，与单一的LSTM模型相比，本文模型的MAE值、MAPE值和RMSE值分别降低了11.13%、11.33%和11.36%. 这表明经过CEEMDAN-FE 分解重构后的序列能提高预测精度，并有效发掘非线性数据中的有用信息.

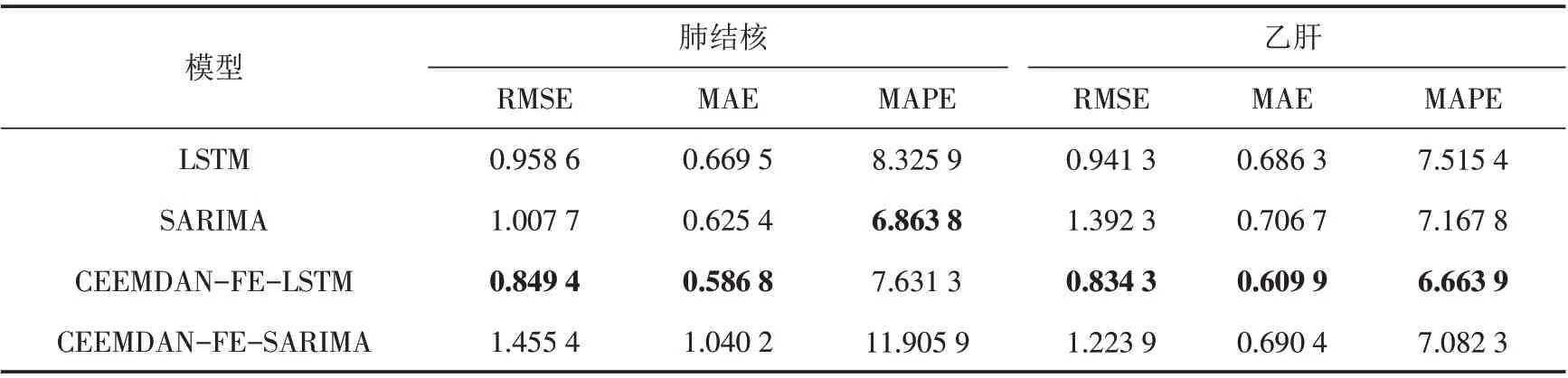
表2 各模型性能指标在肺结核病和乙肝数据集上的对比Tab.2 Comparison of performance indicators of each model in the tuberculosis and hepatitis B datasets

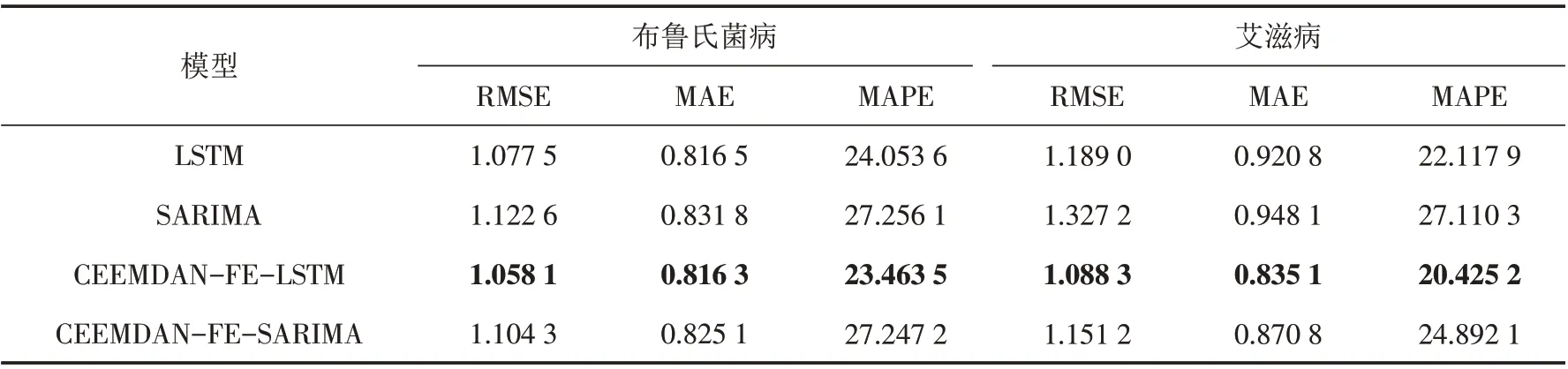
表3 各预测模型性能指标在布鲁氏菌病和艾滋病数据集上的对比Tab.3 Comparison of performance indicators of each prediction model in brucellosis and AIDS datasets

4 结语

根据传染病时间序列具有典型的非线性与非平稳的波动特征，本文提出了CEEMDAN-FE-LSTM 模型应用于常见传染病的预测，并通过模型的预测性能对比，得到如下结论：

1）经过CEEMDAN分解后的时间序列具有不同频率尺度的特征，对分解后的序列进行预测分析有助于掌握患病数据的变化规律. 使用FE算法计算复杂度并重构，得到的重构序列之间的复杂度差异明显，有助于发掘时间序列的隐藏信息，提升运算效率.

2）与经典SARIMA模型相比较，本文提出的CEEMDAN-FE-LSTM 模型具有更好的预测效果，且预测性能更加稳定，充分发挥了LSTM模型在预测非线性的传染病数据上的优势.

本文模型在选定模型参数时使用了多次尝试法选取，在参数寻优上存在局限，后续将在本文模型的基础上，综合考虑优化模型参数，提高模型的适用性.