地铁车轮多边形磨耗对轮轨系统动力特性的影响

刘奇锋，陶功权，梁红琴，卢纯，温泽峰，龙辉

(1.西南交通大学机械工程学院，四川成都，610031；2.西南交通大学牵引动力国家重点实验室，四川成都，610031)

随着城市人口不断增长，越来越多城市采用地铁交通系统以缓解交通压力，地铁车轮磨耗问题也日益突出，车轮多边形作为地铁车轮常见的磨耗形式之一，会导致轮轨关系变差、轨道和车辆部件破坏以及车辆振动噪声异常等现象[1−2]。

针对车轮多边形磨耗对轮轨系统动态响应的影响，国内外学者开展了相关研究。LIU等[3]针对高速列车多边形引起的轮轨动态影响进行了研究，发现当速度大于300 km/h 时，车轮径向偏差的导数可以反映轮轨力的变化趋势。WU等[4]研究发现多边形磨耗会显著增大轮轨垂向力，高阶多边形可能会激发轮对和轴箱的固有模态，导致较大的加速度和轮轴动应力。CHEN等[5]发现随谐波磨耗阶数和波深增大，轮轨垂向力、轮重减载率、扣件力及钢轨振动频率明显增大。肖乾等[6−7]建立了多刚体模型和柔性轮轨模型，分析车轮多边形磨耗对轮轨蠕滑率/力的影响。刘欢等[8]指出当出现多边形磨耗时，机车牵引行为下纵向蠕滑率/力波动显著增大，磨耗指数也显著增大并加剧多边形的磨耗。LIANG等[9]指出在湿轨条件下，多边形磨耗使机车牵引性能明显下降，轮轨出现滑动现象。YANG等[10]发现严重的多边形磨耗不仅对车辆轨道系统的垂向动力学性能有影响，对纵向动力学性能也有显著影响。谢建平等[11]以2阶和3阶谐波磨耗为例，研究了车轮谐波磨耗对轮轨垂向力及车体平稳性的影响。尹振坤等[12]以轮轨垂向动载荷为依据初步建立了高速列车多边形状态下的安全镟修限值。崔大宾等[13]指出车轮径跳相似的3种不同阶次非圆化形态对高速轮轨力的影响不同，高阶车轮多边形对轮轨垂向动力学特性影响较大。杨润芝等[14]建立了考虑轨道、轮对、轴箱、轴承柔性的车辆轨道刚柔耦合动力学模型，分析了多边形对轮对、轴箱、制动盘振动特性的影响，研究制动工况下制动盘不同部位的振动特性。胡晓依等[15]基于ANSYS 和SIMPACK 建立了轮轨柔性的动力学仿真模型，对比了不同仿真模型在以典型高阶多边形激励作为输入时，高速轮轨系统振动的影响规律。

上述文献比较全面地分析了多边形对车辆轨道系统动态响应的影响，但对于多边形和多边形不圆时变率(多边形幅值对时间的一阶导数)在时域中与轴箱加速度和轮轨力的对应关系研究不够深入，因此，本文作者考虑轮轨柔性，基于ANSYS和SIMPACK建立地铁刚柔耦合动力学模型，以实测地铁车轮多边形磨耗为输入，研究时域中多边形幅值变化和不圆时变率与轴箱垂向加速度、轮轨垂向力的对应关系，研究结果可为车轮多边形状态监测提供参考。

1 车辆−轨道刚柔耦合动力学模型

为保证仿真结果的可靠性，需针对不同研究对象建立相应合理的动力学仿真模型，TAO 等[16]指出在地铁运营线路中普遍存在簧下质量与轨道结构耦合共振(P2共振)现象，且地铁车轮多边形容易激发轮轨系统P2 共振；刘孟奇等[17]指出在对车轮多边形等中高频激励进行动力学分析时，考虑轮轨柔性能切实反映轮轨系统固有模态共振等现象。因此，为了研究多边形对轴箱振动和轮轨力的影响，考虑轮对和钢轨的柔性，基于ANSYS和SIMPACK 建立地铁车辆−轨道刚柔耦合动力学模型。图1所示为地铁车辆−轨道耦合动力学模型。

图1 地铁车辆−轨道耦合动力学模型Fig.1 Dynamics model of Metro vehicle−track rigid-flexible coupling

1.1 地铁车辆系统动力学模型

根据某型地铁车辆参数，建立整车多刚体动力学模型，模型包含4 条轮对、8 个轴箱、2 个构架及1 个车体，其中轴箱仅考虑点头自由度，轮对、构架和车体均考虑伸缩、横移、沉浮、测滚、点头和摇头6个自由度。车体、构架、轮对及轴箱视为刚体；一系及二系悬挂使用弹簧阻尼力元模拟，一系垂向减振器、二系垂向减振器、二系横向减振器及横向止挡等均考虑其非线性特征。车轮踏面采用S1002 型面，钢轨采用CN60 型面，车轮与钢轨接触法向力采用HERTZ 接触算法求解，切向力则采用KALKER 简化理论FASTSIM 算法求解。

1.2 柔性轮对模型

SIMPACK 中柔性体是利用有限元软件对有限元模型进行缩减得到的结果文件来生成的，其变形通过模态叠加来实现，柔性体通过主节点与其他部件产生联系，主节点通常具有3 个移动自由度，梁单元则有6 个自由度；主节点可作为SIMPACK中的Marker点从而施加力、铰接、约束等[18]；有限元模型中选取主节点时应尽量保证主节点间隔均匀。为实现轮对的柔性化，在ANSYS中建立轮对有限元模型，采用SOLID 45 单元进行离散，其弹性模量为210 GPa，泊松比为0.28，密度为7 800 kg/m3，单元总数为99 876 个，节点数为102 054个。采用Block Lanczos法对轮对有限元模型进行自由边界模态分析，为减少模型自由度，便于动力学仿真计算，利用Guyan缩减法对有限元模型自由度进行缩减。在对有限元模型进行缩减时，在车轴11处截面选取主节点55个，左、右车轮名义滚动圆上选取主节点各40 个，主节点一共135个，每个主节点均保留其全部自由度，主节点选取如图2紫色节点所示。在动力学仿真分析中考虑轮对400 Hz以内的模态，表1所示为轮对主自由度缩减前、后的模态信息，由表1可知：缩减前、后轮对模态频率的相对误差不超过2%，说明轮对子结构模型比较准确。

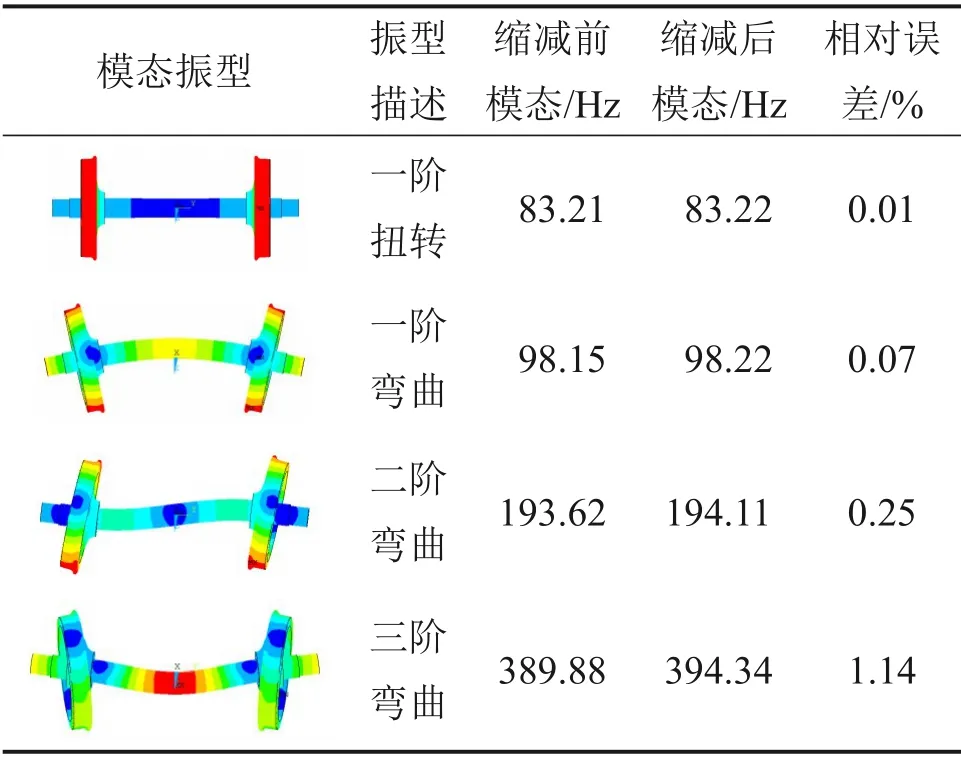
表1 轮对模态对比Table 1 Comparison of wheelset modal

图2 轮对子结构模型Fig.2 Substructure model of wheelset

1.3 柔性钢轨模型

根据CN60钢轨型面建立钢轨有限元模型，将钢轨考虑为Timoshenko梁，采用BEAM188单元进行网格离散。在钢轨上每0.3 m 选取1 个主节点，扣件间隔为0.6 m，钢轨长度为48 m。扣件使用弹簧阻尼力元模拟，利用Python 编制FLEXTRACK模块配置文件，文件包含柔性钢轨在空间中的位置和方向、钢轨引用次数、钢轨主节点位置、外推节点和扣件约束等信息，再利用SIMAPCK 的Nonlinear Flextrack 柔性体模块读取配置文件信息即可实现钢轨柔性化，在SIMPACK动力学仿真分析中考虑钢轨前600阶模态。根据SIMAPCK 用户帮助手册，钢轨端部使用大刚度、大阻尼力元固定，刚度取为1×1010MN/m，阻尼取为1×107kN·s/m。钢轨及扣件部分参数见表2。

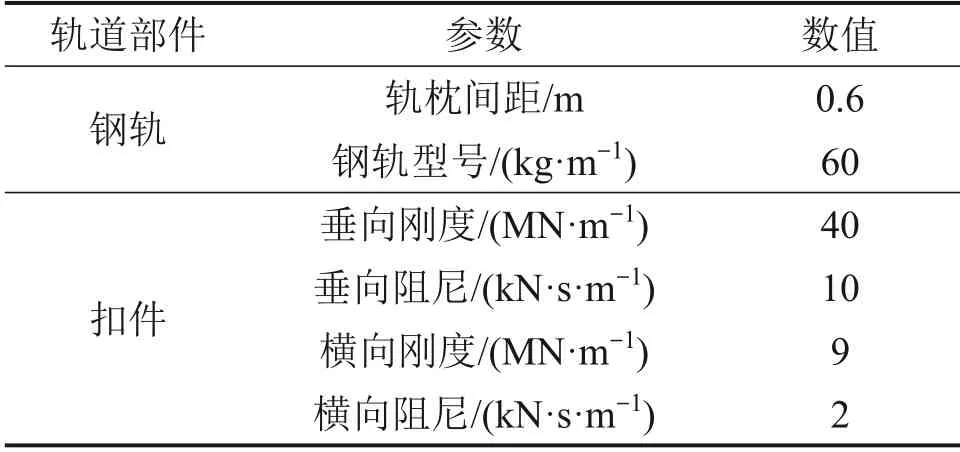
表2 钢轨及扣件部分参数Table 2 Parameters of rail and fastener

1.4 模型验证

为验证模型的可靠性，参考文献[17]中地铁车辆试验数据，以车轮实测不圆度数据为输入，如图3所示，由图3可知：车轮存在明显的偏心、6阶及13阶多边形。车辆运行速度为75 km/h时的仿真结果和试验数据如图4所示，由图4可知：仿真数据与试验数据较为吻合，频域图均在48，64 和102 Hz处有明显峰值，48 Hz与102 Hz恰好分别为75 km/h 时6 阶和13 阶多边形的通过频率，利用SIMAPCK对车辆轨道系统作特征值分析发现P2共振频率约为63 Hz，因此，图4(b)中64 Hz 为轮轨系统P2 共振频率。然而，仿真时采用的美国5 级谱轨道激励与多边形激励并不能完全模拟实际条件下轨道和车轮轮廓的磨损状态，且车辆轨道模型进行了一定简化等因素，在100 Hz 以上的一定范围内仿真结果与试验结果存在一定差异，但多边形激振频率以及P2 共振频率在仿真模型中得到了充分反映，故该仿真模型可靠。

图3 车轮实测不圆度Fig.3 Wheel out-of-roundness measured

图4 模型验证Fig.4 Model validation

2 多边形激励下轴箱振动和轮轨力的动态响应

2.1 车轮多边形激励

多边形磨耗是指车轮半径沿车轮周向周期性变化的磨耗现象，国际上常采用含有1～N阶谐波的Fourier级数形式的位移函数Z0(t)来表示[3]，即

式中：Ai为第i阶车轮多边形的幅值；φi为第i阶车轮多边形的相位；v为车辆运行速度；r为车轮平均半径；t为时间。

根据式(1)，Z0(t)的一阶导数可表示为

本文将不圆时变率定义为Z0(t)的一阶导数。地铁运营过程中常出现低阶和高阶多边形磨耗，低阶多边形如3阶[19]、5～8阶[2]，高阶多边形如12～14阶[20]、11～16阶[21]。因此，本文基于大量的现场实测地铁车轮不圆度数据，选取3种典型的多边形磨耗为例进行研究。图5所示为3种地铁车轮多边形磨耗的阶次图及直角坐标图，其中磨耗1为低阶多边形，磨耗2 和磨耗3 为高阶多边形，磨耗1 的主要阶次为7 阶，径跳约为0.26 mm；磨耗2 主要为13阶多边形，径跳约为0.17 mm；磨耗3则是15阶多边形，径跳约为0.28 mm。

图5 3种典型多边形磨耗Fig.5 Three typical polygonal wears

2.2 多边形磨耗对轴箱加速度的影响

仿真考虑美国5级谱轨道激励，在车辆一位轮对上施加多边形激励，右侧车轮轴箱上设置传感器以获得轴箱垂向加速度。图6所示为当速度为60 km/h 时，3 种多边形磨耗激励下轴箱垂向加速度与多边形幅值/不圆时变率的时域对应图，从图6可以看出：磨耗1，2 和3 的多边形磨耗的轴箱加速度峰值分别为24.21，18.73 和26.39 m/s2。对于磨耗2 和磨耗3，轴箱垂向加速度的极大值均出现在多边形由波谷到波峰的上升阶段，极小值则出现多边形由波峰到波谷的下降阶段，而磨耗1轴箱垂向加速度极大值出现在多边形波谷附近，极小值则出现在多边形波峰附近。由此可见轴箱垂向加速度极值与多边形不圆顺极值有一定的相位差，而多边形磨耗可由含有1～N阶谐波的Fourier 级数形式的位移函数来表示，因此考虑对多边形磨耗Z0(t)求一阶导数，以进一步研究轴箱垂向加速度与不圆时变率的对应关系。

图6 轴箱垂向加速度与不圆顺幅值/不圆时变率的对应关系Fig.6 Relationship between vertical acceleration of axle box and amplitude or time-varying rate of out-of-round

为了深入了解多边形磨耗与轴箱垂向加速度的关系，将轴箱垂向加速度与不圆时变率进行对比，从图6可以看出：磨耗2 及磨耗3 的轴箱垂向加速度与不圆时变率具有较好的对应关系，轴箱加速度的极大值和极小值分别出现在不圆时变率的波峰和波谷处，且轴箱垂向加速度的变化趋势与不圆时变率相似，但磨耗1中轴箱垂向加速度与不圆时变率的对应关系存在较为明显的相位差。

为衡量不圆时变率与轴箱加速度的线性对应程度，分别对3种情况下不圆时变率和轴箱垂向加速度进行最小二乘法线性拟合，用决定系数R2来评价线性拟合优度，即

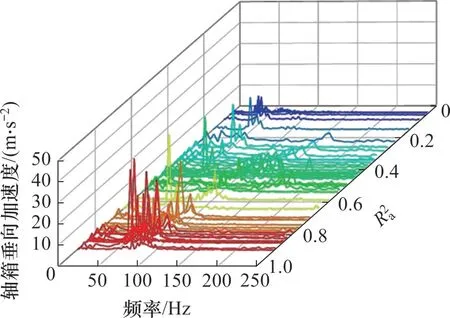
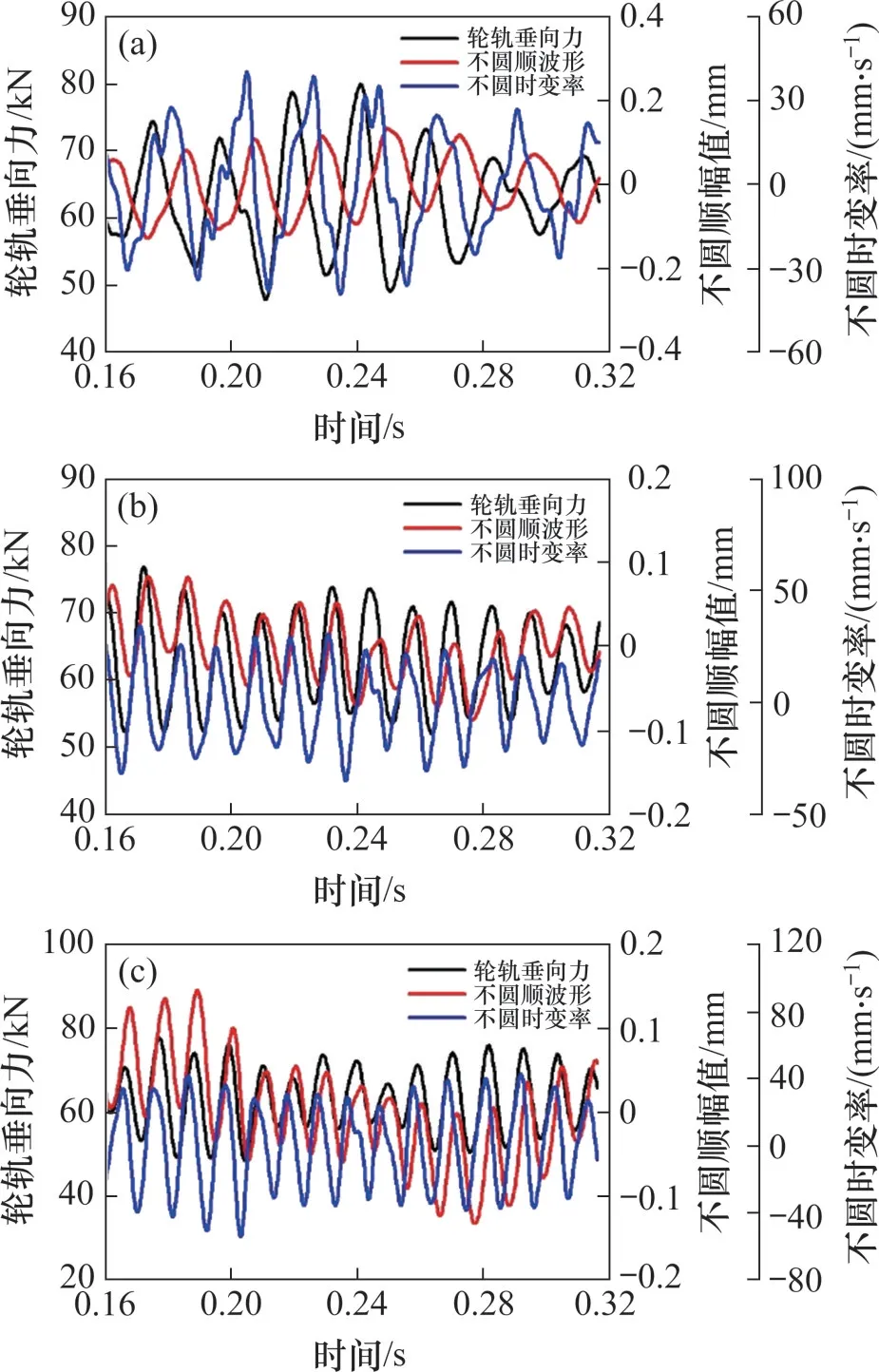
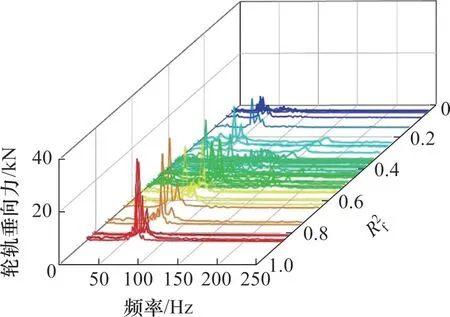
式中：yi为样本真实值；为样本的平均值；yi为样本预测值；n为样本数量。R2越接近1，线性拟合预测效果越好，并称为样本的复相关系数，R越大，线性相关性越强[22]。一般认为当R≥0.8 时，2 个变量之间高度相关；当0.5≤R<0.8时，中度相关；当0.3≤R<0.5 时，低度相关；当0

从图7可以看出：在3种磨耗情况下，磨耗1，2 和3 的R2a分别为0.09，0.85 和0.76，可见磨耗2和磨耗3不圆时变率与轴箱垂向加速度的决定系数较高，线性相关性也较强。磨耗1情况下决定系数仅为0.09，其线性拟合效果较差。

图7 不圆顺幅值及不圆时变率对轴箱垂向加速度的影响Fig.7 Influence of amplitude and time-varying rate of wheel out-of-roundness on vertical acceleration of axle box

由图5可知：磨耗2主要为13阶多边形，磨耗3主要为15阶多边形，而磨耗1主要为7阶多边形，当列车速度为60 km/h 时，3 种磨耗引起的轴箱垂向加速度与不圆时变率的对应关系差异较大，因此，考虑运行速度是否影响轴箱加速度与不圆时变率的对应关系。仿真工况假定车辆运行速度为40～120 km/h，速度间隔为5 km/h，其仿真结果如图8所示。

从图8可以看出：速度对决定系数有较大影响，对于磨耗1，在85～120 km/h 内其决定系数均高于0.70，在40～55 km/h 内决定系数近乎为零；对于磨耗2，在45～70 km/h内决定系数均大于0.70；而对于磨耗3，则在40～60 km/h 内决定系数大于0.70，不同磨耗情况在对应的速度范围内不圆时变率与轴箱加速度具有较高的决定系数。

将3种车轮磨耗在不同速度下的轴箱垂向加速度频谱按照轴箱垂向加速度与车轮不圆时变率决定系数的大小绘制，如图9所示，从图9可以得知：在30～190 Hz都存在较为明显的峰值频率，恰好覆盖3 种磨耗的激振频率；当决定系数大于0.7时，其峰值频率主要集中在60～95 Hz频率范围内。结合图8结果可知，速度影响多边形的通过频率，多边形激振频率则直接影响轴箱垂向加速度与车轮不圆时变率的决定系数。

图8 不圆时变率与轴箱垂向加速度的决定系数Fig.8 Determination coefficients between time-varying rate of out-of-round and vertical acceleration of axle box

图9 不同决定系数下轴箱垂向加速度频谱Fig.9 Frequency spectrum of axle box vertical acceleration with different determination coefficients

当多边形激振频率在60～95 Hz 时，车轮不圆时变率与轴箱垂向加速度的回归决定系数较大。通过SIMAPCK对车辆轨道系统进行特征值分析发现轮轨系统P2共振频率为63 Hz，约束状态下的一阶扭转频率、一阶垂弯频率及一阶横弯频率分别为83，88 和93 Hz；其各部分模态频率恰好落在60～95 Hz 频率段内，因此，在该频率段内不圆时变率与轴箱垂向加速线性相关性较强的原因是多边形通过频率与轮轨系统的固有频率发生了耦合。所以多边形激振频率在60～95 Hz 频段内时，可以利用不圆时变率来预测轴箱垂向加速度，反之也可以根据轴箱垂向加速度来反映车轮不圆时变率，从而进一步估计车轮不圆顺的形状。

2.3 多边形磨耗对轮轨垂向力影响

多边形磨耗对轮轨垂向力也有较大影响，图10所示为当速度为60 km/h时，轮轨垂向力与多边形幅值/不圆时变率的时域对应关系。从图10可以看出：磨耗1，2 和3 状态下的轮轨垂向力最大值分别为80.0，76.9 和77.5 kN。对于磨耗2 和磨耗3，轮轨垂向力极大值出现多边形由波谷到波峰的上升阶段，极小值则出现在多边形由波峰到波谷的下降阶段；轮轨垂向力在相位上超前于多边形不圆顺波形，滞后于不圆时变率。而对于磨耗1，其轮轨垂向力极大值出现在不圆时变率由波谷到波峰的上升阶段，极小值则出现在不圆时变率由波峰到波谷的下降阶段；轮轨垂向力在相位上超前于多边形不圆顺波形和不圆时变率。R2f为不圆时变率与轮轨垂向力的决定系数，经计算，磨耗1，2 和3 的R2f分别为0.08，0.48 和0.43，3 种磨耗情况下差异明显，且均比相同速度下的R2a的差异小。

图10 轮轨垂向力与不圆顺幅值/不圆时变率的对应关系Fig.10 Relationship between wheel-rail vertical force and amplitude or time-varying rate of out-of-round

图11所示为不同速度下轮轨垂向力与不圆时变率决定系数的变化曲线，从图11可以看出：图8稍有差异，3种车轮磨耗仅在较小的速度范围内有较高的决定系数R2f，磨耗1在85～95 km/h内决定系数大于0.70，磨耗2在45～50 km/h内决定系数大于0.70，磨耗3 则在40～45 km/h 内有较大的决定系数。

图11 不圆时变率与轮轨垂向力的决定系数Fig.11 Determination coefficients between time-varying rate of out-of-round and wheel-rail vertical force

将上述3种车轮磨耗在不同速度下的轮轨垂向力频谱按不圆时变率与其决定系数的大小绘制，结果如图12所示，由图12可知：与轴箱垂向加速度类似，在30～190 Hz 间存在较为明显的峰值频率，当峰值频率在58～69 Hz 时，其对应的决定系数大于0.70，而当峰值频率不在这个频率段时，其对应的决定系数均较小，可见当多边形激振频率在P2 共振频率附近时，不圆时变率和轮轨垂向力有较好的线性拟合效果。因此，在P2 共振频率附近利用轮轨垂向力来预测不圆时变率效果较好。

图12 不同决定系数下轮轨垂向力频谱Fig.12 Frequency spectrum of wheel-rail vertical force with different determination coefficients

3 结论

1)所建立的地铁车辆−轨道刚柔耦合动力学模型能准确反映车辆实际情况下轮轨系统动力特性，使仿真计算结果更贴近实际。

2)车轮多边形激振频率在60～95 Hz 时，不圆时变率与轴箱垂向加速度的决定系数大于0.70；激振频率在P2 共振频率附近时，不圆时变率与轮轨垂向力的决定系数大于0.70，线性相关性较强，这与轮轨系统的固有模态耦合有关。

3)不圆时变率与轴箱垂向加速度和轮轨垂向力在一定频段内有较好的线性拟合效果，据此可考虑利用轴箱垂向加速度和轮轨力来评估车轮多边形磨耗状态。