壁面阵列梯形凸起的矩形通道传热特性

何 璟，王良璧，杨 成

（1.兰州交通大学 化学化工学院，兰州 730070；2.兰州交通大学 机电工程学院，兰州 730070；3.兰州交通大学 铁道车辆热工教育部重点实验室，兰州 730070）

20世纪70年代的能源危机促进了强化传热技术的研究和发展.增大单位体积的传热面积、提高传热系数是强化传热的主要途径.通道内设置肋片与凹槽广泛应用于传热领域.近年来对通道内布置肋片和凹槽强化传热技术主要反映在斜肋、V型肋、W型肋等结构上.Kim等［1］通过比较k-ε模型、k-ω模型和SST k-ω模型，最后选用SST k-ω模型计算雷诺数Re=10 000～30 000范围内60°倾斜肋传热.Liou［2］等通过双通道90°肋组成平行四边形通道进行了粒子图像测速和红外热成像测量传热流动特性研究，发现肋顶部和中部的传热和流动动力学机制不同.Solanki［3］对攻角75°时交错倾斜离散肋的排布进行了研究，发现间隙位置比为0.3时传热效率最高.Sivakandhan［4］等对一种混合倾斜肋片太阳能空气加热器的传热流动特性进行了研究，结果表明随着流速增加，传热效率达到最大，然后随着质量流量的进一步增加呈下降趋势，并通过分析得到了肋片最佳高度、最佳间距和最佳倾角.Sharma［5］等对矩形通道内的交替实心和收敛狭缝肋进行了传热和流动研究，发现收敛狭缝肋大大提高了下游附近的传热速率，有助于避免局部热点的形成.Ali［6］等研究发现，与方形肋相比，梯形肋片在肋片下游具有更高的传热速率.

马超［7］对平行肋、V形肋、倒V形肋结构开展了蒸汽和空气冷却的传热实验研究，结果表明，蒸汽和空气的平均努塞尔数随着肋角从90°减小到45°而增加.杨卫华［8-9］对方形通道双面肋片进行了实验研究，结果表明，肋间距与肋高的比值对肋通道的传热效果呈先增加后减小的趋势，对称肋比交错肋的努塞尔数更高.周明轩［10］、王培枭［11］也进行了相似的研究，得到与［8-9］类似的结论.涂立［12］数值模拟了肋高与肋间距之比、肋片倾斜角度、肋片截面形状、不同方式排列的间断肋对带肋壁面换热效果的影响.结果表明：随着肋间距与肋高之比的增大或随着肋片倾斜角度的增大，带肋壁面的换热强度均呈现先增大后减少的趋势，梯形截面肋片较方形、椭圆形的效果更佳.刘国鹏［13］通过研究发现：在一定范围内，梯形肋高宽比和肋间距越大、等腰梯形底角越小，换热效果越好，但阻力系数也越大；当梯形肋几何参数一定时，随着雷诺数的增大，传热性能越好，阻力系数越小.Li［14］通过对多V型通道进行了数值分析，并用遗传基因算法对V型肋间距、肋高度、肋角度进行了优化，得到最佳结构.Zheng［15］等对矩形通道中五种不同矩形或梯形孔组成的肋进行了数值研究，发现角度最小的梯形孔流场，湍流强度最高，从而产生的强化传热最强，压力损失也最大.

本文采用数值计算的方法，研究了壁面阵列梯形凸起的矩形通道传的热特性，对于不同凸起结构，如凸起角度、凸起间距影响强化传热的机理进行了分析，并对其综合传热予以评价，旨在研究壁面阵列梯形凸起对于强化矩形通道内传热效果的增强程度.

1 物理模型与控制方程

1.1 物理模型

壁面有阵列双端倒角长方状梯形凸起时矩形通道的物理模型如图1所示.为了探讨流体充分发展时在该结构通道的流动与阻力情况，将通道分为三段如图1（a）所示，进口段长为300 mm，测试段长为165 mm，出口段为300 mm保证测试段不受回流影响，双端倒角长方状梯形凸起结构的高度固定为e=3 mm，倾斜角用β表示.图1（b）为矩形通道测试段及加热面的对称下半部分的示意图，对壁面阵列双端倒角长方状梯形凸起的矩形通道的底面加热，通道高度H=20 mm.阵列双端倒角长方状梯形凸起结构的物理参数如图1（c）所示，长方状梯形凸起结构的攻角用α表示．两边间距d2=d1=10 mm，长方底面长度l=16 mm，宽度w=7 mm，矩形通道的宽为W=40 mm，长为L=165 mm.矩形通道的当量直径为De=4A／P=27 mm.流动和几何参数的变化范围见表1，分别对于不同相对肋间距、倾斜角来研究矩形通道的传热特性.

表1 参数的变化范围Tab．1 Variation range of parameters

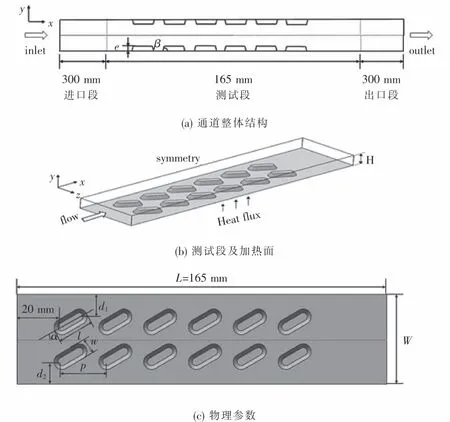
图1 长方状梯形凸起矩形通道的结构示意Fig．1 Structural diagram of rectangular Duct with rectangular hole shape trapezoidal protrusion

1.2 控制方程及边界条件

工作介质为水，在雷诺数6 000至16 000范围内，假定水为不可压缩流体且通道内的流动为稳态的.湍流的控制方程表示如下：

连续性方程：

动量方程：

能量方程：

其中

边界条件：通道进口为速度进口，水的进口温度恒定为313 K，出口边界为outflow出口，并假定所有固体壁面为无滑移边界条件.通道进口段和出口段的所有壁面为绝热条件，测试段底部加热并给定恒定热流密度333 W／m2，上表面为对称边界条件，其余面为绝热边界条件.

进口截面：

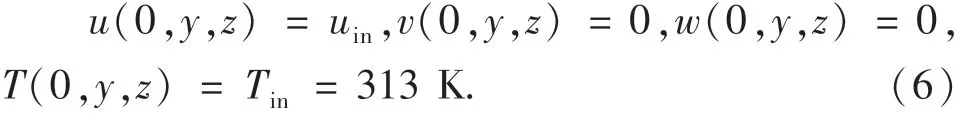
出口截面：

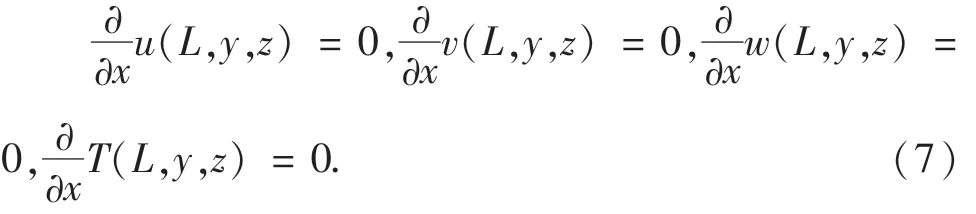
加热面：

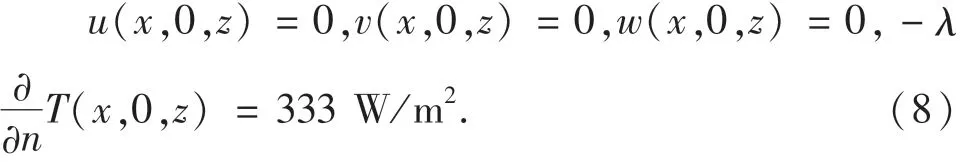
所有绝热壁面：

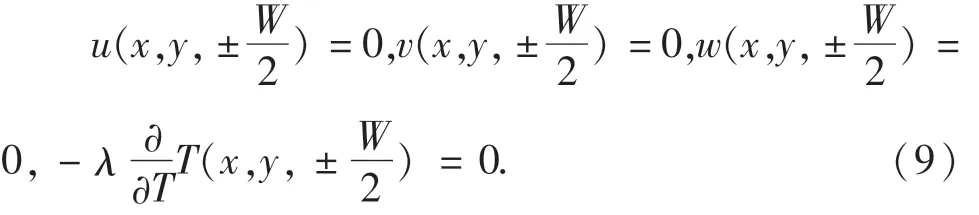
对称面：

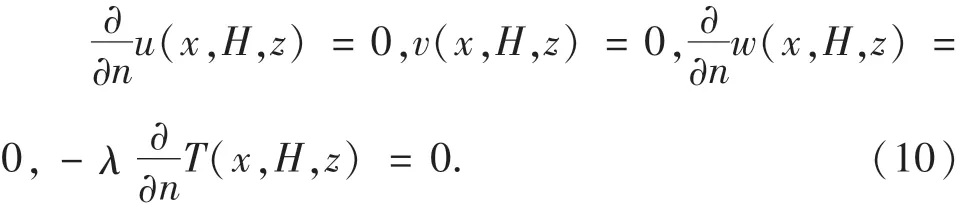
雷诺数：

其中De=4A／P=27 mm．

局部换热系数：

其中：q为局部热流密度，W／m2；tw为局部壁面温度，K；tf为质量加权平均求出的参考温度．

局部努塞尔数：

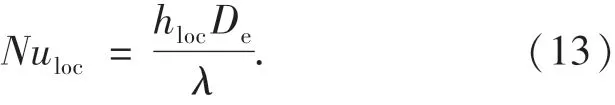
平均努塞尔数：

光滑矩形通道的Nu0采用Gnielinski计算公式计算［16］

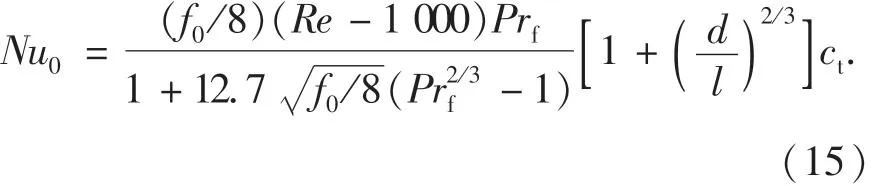
其中阻力系数f0按Filonenko公式计算：

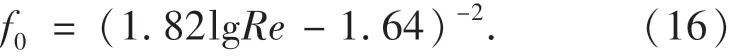
壁面阵列长孔状梯形凸起矩形通道的阻力系数f按下式计算：

等泵功综合传热因子［17］：

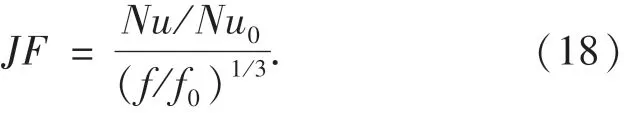
2 网格划分及数值计算方法

本文选用商业软件Fluent进行数值计算，网格划分采用mesh划分混合网格，并将边界层网格细化.网格划分结果如图2所示.进口段与出口段为结构化网格，测试段由于底面阵列双端倒角长方状梯形凸起，其结构较复杂故采用四面体网格.

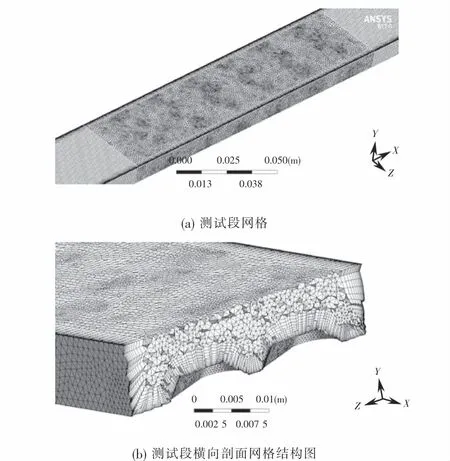
图2 网格划分结果Fig．2 mesh results

数值解的网格独立性考核选择了三组不同密度的网格，网格数如表2中所示.不同网格密度下，平均换热Nu与阻力系数f的最大误差均小于2%.综合考虑网格质量、计算精度和计算效率，文中所有计算结果均采用网格数为194万左右.

表2 数值结果网格独立性考核（Re＝6 000）Tab．2 The result dependence on the grid size

选择SIMPLEC算法作为压力速度耦合求解器，动量项、湍动能项、湍流耗散项、压力及能量项均采用二阶迎风格式以保证计算精度，梯度项采用最小二乘单元法，能量方程和其它方程的残差值设置为10-8.为了验证湍流模型的准确性，选取Standard kε、RNG k-ε、Realizable k-ε、SST k-omega四种湍流模型对光滑的矩形通道进行数值计算，并将计算得到的Nu0与Gnielinski公 式（15）的 计 算 值，f0与Filonenko公式（16）的计算值进行对比.结果如图3（a）所示，Nu0的最大误差分别是20.99%、32.82%，21.01%、8.41%，如图3（b）所示，f0的最大误差分别是13.42%、14.75%，14.74%、10.36%，发现SST k-omega湍流模型的误差最小，因此选用SST k-omega低雷诺数湍流模型用于后续模型的数值计算.

图3 不同湍流模型对于光滑的矩形通道Nu0、f0的对比Fig．3 Comparison of different turbulence models for smooth rectangular channel Nu0 and f0

3 结果讨论

图4为α=30°、p／De=0.741，不同倾斜角β时，Nu、f随Re的变化．从图中可以看出，在倾斜角β相同时，Nu的值随着Re的增大而增大，而f的值随着Re的增大而逐渐减小．在Re由6 000增大至16 000的范围内，当倾斜角β=45°时，Nu的值由181．7增大至368．4，增大2．03倍，f的值由0．103减小至0．096，减小6．80%；当倾斜角β=60°时，Nu的值由197．8增大至373．4，增大1．89倍，f的值由0．124减小至0．099，减小20．16%；当倾斜角β=90°时，Nu的值由186．3增大至350．0，增大1．88倍，f的值由0．106减小至0．093，减小12．23%．由图还可以看出，在相同Re时，倾斜角β=60°时的Nu数和f的值均大于倾斜角β=45°和β=90°的Nu数和f的值，强化传热效果最好.梯形凸起对其前方来流的阻滞作用造成流体的分离和流动方向的转变，进而引起凸起位置上方主流过流截面的收缩，形成顶部位置的分离泡和主流的局部加速现象，进入梯形凸起结构下游的突扩通道后流体逐渐减速扩张，并在一定距离的位置再附于通道下壁面，在梯形凸起正后方一定范围内就形成一个较大的低速回流区.因此，梯形状凸起结构的存在破坏了流体的壁面边界层，引起流体从壁面的分离与再粘附，增加了近壁区流体的湍流度，从而提高了流体与壁面间的对流换热系数.

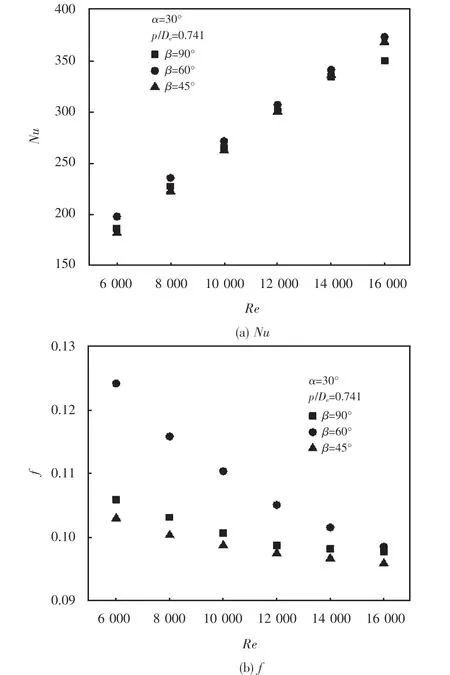
图4 不同倾斜角时Nu、f随Re的变化趋势Fig．4 The change trend of Nu and f with Re at different angles of inclination

图5为α=30°、β=60°，不同凸起间距时，Nu、f随Re的变化趋势．由图可以看出，在Re由6 000增大至16 000的范围内，当凸起间距p为15 mm，即p／De=0.556时，Nu的值由160．1增大至314．3，增大1．96倍，f的值由0．070 2减小至0．062 6，减小10．83%；当凸起间距p为20 mm，即p／De=0.741时，Nu的值由197．8增大至373．4，增大1．89倍，f的值由0．124减小至0．099，减小20．16%；当凸起间距p为25 mm，即p／De=0.926时，Nu的值由164．2增大至328．8，增大2．0倍，f的值由0.078减小至0.068，减小12.82%.由图还可以看出，在相同Re时，凸起间距p为20 mm时，Nu的值、f的值均大于凸起间距p为15 mm或25 mm时的Nu数和f的值，说明p／De=0.741时其对应的Nu、f的值均最大，强化传热效果最好．当图中相对凸起间距为p／De=0.556较低时，梯形凸起前的气流保持了较高的流向速度，没有出现分离区，同时梯形凸起后的回流区也得到了有效抑制，流体通过凸起形成的射流将低速回流区抬离下壁面并提高了紧邻凸起的下游壁面附近气流的速度；当相对凸起间距为p／De=0.926较高时，截面上凸起前部出现了流动分离现象，而凸起后的回流区较梯形凸起的有所减小，此时梯形凸起的射流压缩了回流区的上边界、使再附点的位置提前.

图5 不同凸起间距时Nu、f随Re的变化趋势Fig．5 The change trend of Nu and f with Re at different protrusion spacings

3.1 不同结构参数对于传热的影响

图6为α=30°、p／De=0.741，不同倾斜角β时，Nu／Nu0、f／f0随Re的变化，从图中可以看出，在倾斜角β相同时，Nu／Nu0的值随着Re的增大而减小，f／f0的值随着Re的增大而逐渐增大．在Re由6 000增大至16 000的范围内，当倾斜角β=45°时，Nu／Nu0的值由2．65减小至2．52，减小4．91%，f／f0的值由2．98增大至3．87，是Re为6 000时的1．3倍；当倾斜角β=60°时，Nu／Nu0的值由2．88减小至2．55，减小为Re为6 000时的88．54%，f／f0的值由3．59增大至3．97，是Re为6 000时的1．11倍；当倾斜角β=90°时，Nu／Nu0的值由2．72减小至2．39，减小为Re为6 000时的88．1%，f／f0的值由3．06增大至3．54，是Re为6 000时的1．16倍．由图还可以看出，在相同Re时，倾斜角β=60°时，Nu／Nu0、f／f0均大于倾斜角β=45°或β=90°时的值，并在低Re范围内差别更大，说明壁面有阵列双端倒角长方状梯形凸起时矩形通道的结构在倾斜角β=60°的时强化传热效果最好，且在低雷诺数范围内强化传热效果更佳，但在增强传热的同时也增大了阻力．可以得到，对于壁面阵列双端倒角长方状梯形凸起结构，在倾斜角β相同时，在雷诺数较低的情况下，强化传热效果更好；在相同Re时，倾斜角β=60°时的传热效果最优，但增强传热的同时也增大了流体阻力，倾斜角β过大或过小都会对强化传热效果减弱.

图7为α=30°、β=60°，不同凸起间距时Nu／Nu0、f／f0随Re的变化．从图中可以看出，在凸起间距相同时，Nu／Nu0的值随着Re的增大而减小，f／f0的值随着Re的增大而逐渐增大．在Re由6 000增大至16 000的范围内，当凸起间距p为15 mm，即p／De=0.556时，Nu／Nu0的值由2．34减小至2．15，减小8．12%，f／f0的值由2．02增大至2．52，是Re为6 000时的1．25倍；当凸起间距p为20 mm，即p／De=0.741时，Nu／Nu0的值由2．88减小至2．55，减小为Re为6 000时的88．5%，f／f0的值由3．59增大至3．97，增大1．11倍；当凸起间距p为25 mm，即p／De=0.926时，Nu／Nu0的值由2．39减小至2．25，减小5．86%，f／f0的值由2．27增大至2．73，是Re为6 000时的1．20倍．由图还可以看出，在相同Re时，凸起间距p为20 mm，即p／De=0.741时，Nu／Nu0、f／f0均大于凸起间距p为15 mm或p为25 mm时的值，说明壁面有阵列双端倒角长方状梯形凸起时矩形通道的结构在p／De=0.741的时强化传热效果最好，增强传热的同时也增大了阻力.p／De=0.556时的Nu／Nu0、f／f0的值均最小，换热相对最差．可以看出，对于壁面有阵列双端倒角长方状梯形凸起结构，在凸起间距p相同时，在雷诺数较低的情况下，强化传热效果更好；在相同Re时，凸起间距p=20 mm时的传热效果最优，但增强传热的同时也增大了流体阻力，凸起间距过大或过小都会对强化传热效果减弱.

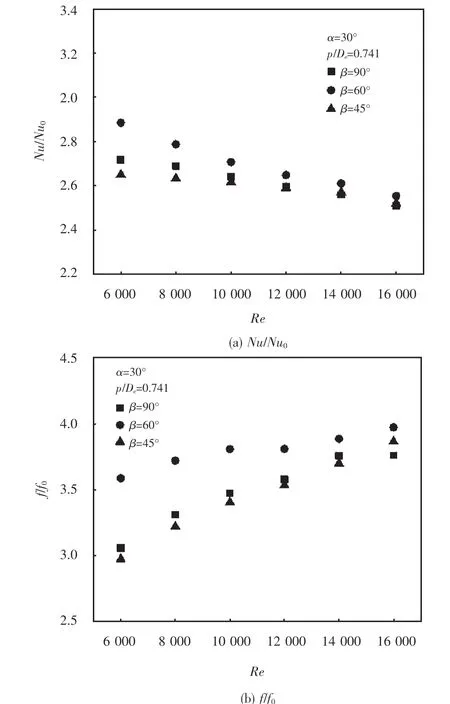
0图6 不同倾斜角时Nu／Nu0、f／f0随Re的变化趋势Fig．6 The change trend of Nu／Nu0 and f／f0 with Re at different angles of inclination

图7 不同凸起间距时Nu／Nu0、f／f0随Re的变化趋势Fig．7 The change trend of Nu／Nu0 and f／f0 with Re at different protrusion spacings

图8为Re=8 000、α=30°、p／De=0.741时，不同β对应的底部加热面局部努塞尔数的分布图，从图中可以看出，Nuloc的最值主要分布在梯形凸起前区域，这是由于凸起前的区域流体受到阻滞发生分离，导致局部努塞尔数迅速增大.当β=60°时，凸起前Nuloc的最值分布区域相比β=90°、β=45°更大，因此其对应的平均努塞尔数的值更大，这与图6所示的Nu／Nu0的结果一致.

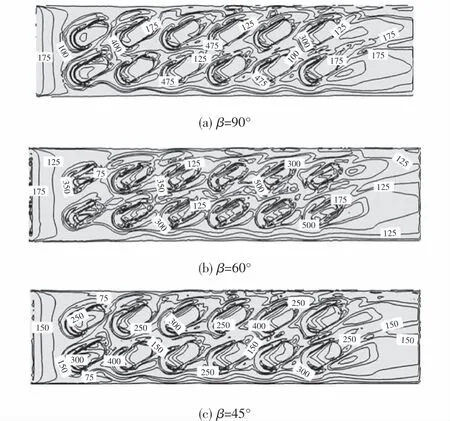
图8 Re＝8 000、α＝30°、p／D e＝0．741时，局部努塞尔数分布Fig．8 Local Nusselt number distribution at Re＝8 000，α＝30°

图9为Re=8 000、α=30°、β=60°时不同凸起间距p对应的底部加热面的局部努塞尔数的分布图，从图中可以看出，凸起间距对于流动与传热有着一定的影响，p／De=0.741时凸起前局部努塞尔数最值分布区域最大，其对应的换热能力最强，这与图7对应的Nu／Nu0结果一致.因此过大或过小的肋间距并不是最优的选择.

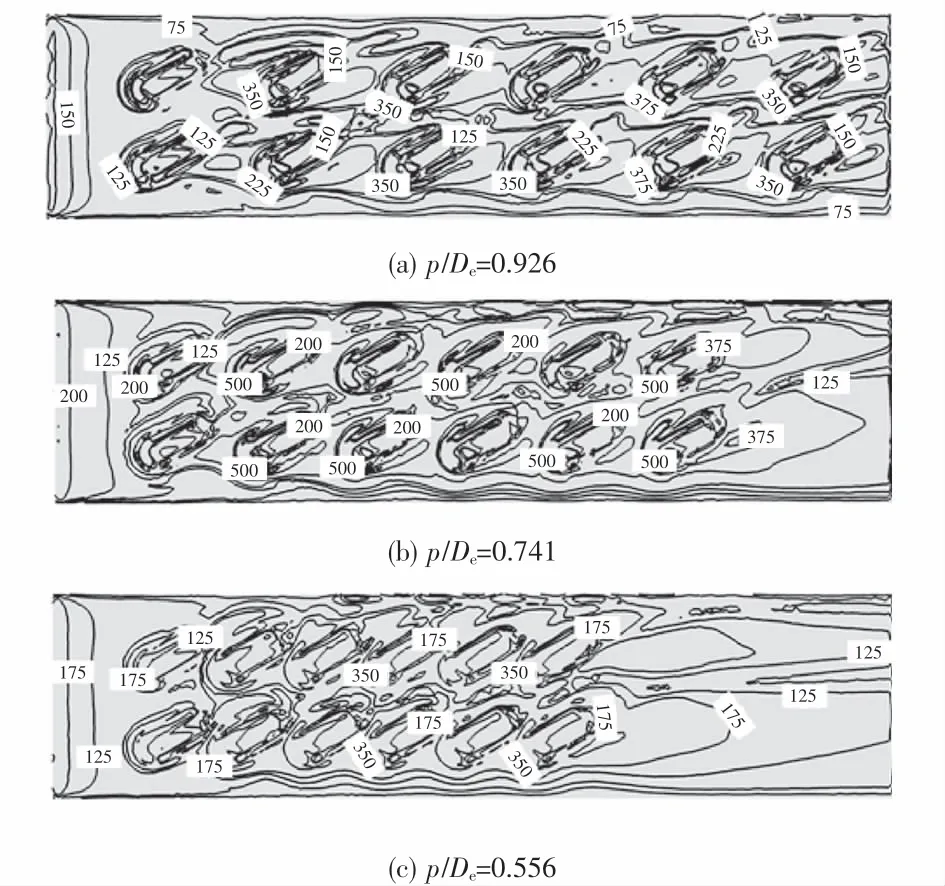
图9 Re＝8 000、α＝30°、β＝60°时，局部努塞尔数分布Fig．9 Local Nusselt number distribution at Re＝8 000，α＝30°，β＝60°

3.2 综合传热评价

由以上分析可知，不同倾斜角、不同凸起间距对壁面有阵列双端倒角长方状梯形凸起结构的均能提高强化传热效果，但在增强传热的同时也增大了阻力.本文采用等泵功综合传热因子JF评价综合传热效果．

图10为等泵功综合传热因子JF随Re的变化，从图中可以看出，在倾斜角β或凸起间距p相同时，JF随Re的增加而减小．在Re由6 000增大至16 000的范围内，当倾斜角β=45°时，JF的值由1．84减小至1．61，减小为Re为6 000时的87．50%；当倾斜角β=60时，JF的值由1．88减小至1．61，减小为Re为6 000时的85．63%；当倾斜角β=90°时，JF的值由1．87减小至1．54，减小为Re为6 000时的82．35%．当凸起间距p为15 mm，即p／De=0.556时，JF的值由1．85减小至1．58，减小为Re为6 000时的85．41%；当凸起间距p为20 mm，即p／De=0.741时，JF的值由1．88减小至1．61，减小为Re为6 000时的85．64%；当凸起间距p为25 mm，即p／De=0.926时，JF的值由1．82减小至1．61，减小为Re为6 000时的88．46%．由图还可以看出，在Re相同时，倾斜角β不同时，JF的值差别不大；凸起间距p=20 mm时，JF的值优于凸起间距p=15 mm或凸起间距p=25 mm时的值.倾斜角β或凸起间距p相同时，在雷诺数较低的情况下，壁面阵列长方状梯形凸起的矩形通道的综合性能JF更好；在雷诺数相同时，不同倾斜角对综合传热能力JF差别不大；凸起间距过大或过小都会对综合传热能力JF减弱.

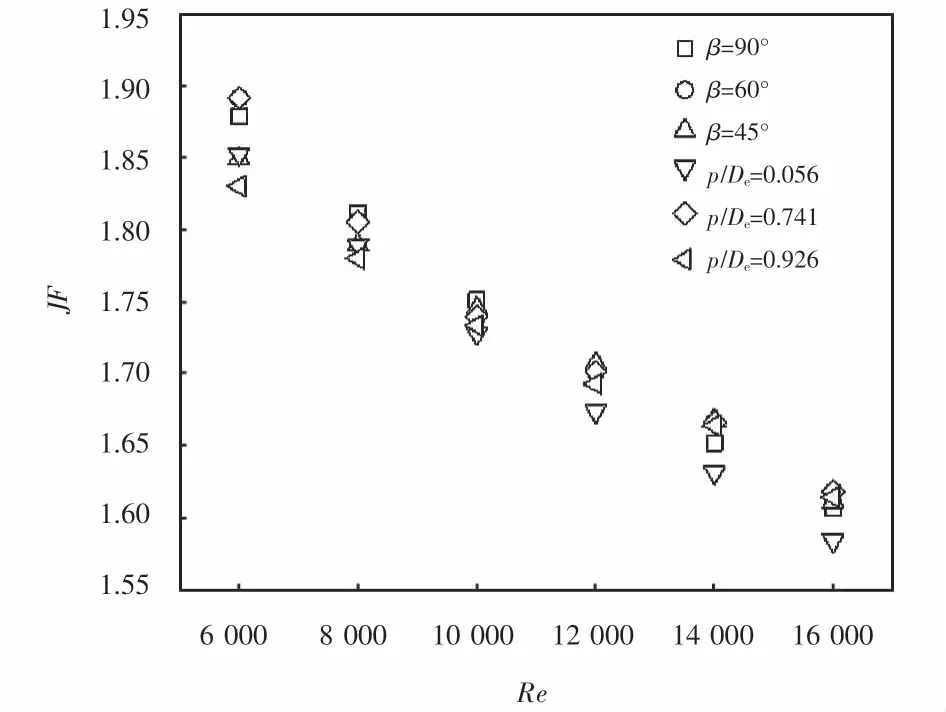
图10 综合传热因子Fig．10 Comprehensive heat transfer performance factor with Re at different angles of inclination and relative protrusion spacings

4 结论

论文通过数值方法分析了壁面阵列双端倒角长方状梯形凸起的矩形通道传热特性、流动特性，并用综合传热因子JF评价了长方梯形凸起的倾斜角、凸起间距对传热特性的影响．论文结果总结如下：

1）阵列某一倾斜角β或某一凸起间距p组成的双端倒角长方状梯形凸起传热通道，都具有强化传热效果，且在雷诺数较低的情况下，强化传热效果更好．

2）当肋攻角α=30°、倾斜角β=60°时，相对凸起间距p／De=0.741对应的矩形通道的换热性能最好，倾斜角β，凸起间距p／De过大或过小都会对强化传热效果减弱.

3）JF随着Re的增大而减小，等泵功综合传热因子JF值介于1．6至1．9之间，在Re相同时，不同倾斜角对综合传热能力JF差别不大；凸起间距过大或过小都会对综合传热能力JF减弱；倾斜角β或凸起间距p相同时，在雷诺数较低的情况下，壁面阵列长方状梯形凸起的矩形通道的综合性能JF更好.