不同翘曲位移函数对薄壁箱梁剪力滞效应的影响

黄洪猛，张元海

（1.兰州交通大学 土木工程学院，兰州 730070；2.西北民族大学 土木工程学院，兰州 730030）

箱形截面由于抗弯抗扭性能良好被广泛应用于桥梁结构中，而腹板间距较大的箱形梁，对称弯曲时变形不服从平截面假定，存在剪力滞效应.剪力滞效应是箱梁翼板出现横向裂缝的主要原因之一，不容忽视［1］.目前，基于最小势能原理的能量变分法是分析薄壁箱梁剪力滞最常用的解析法，而采用该方法的前提是确定能合理描述剪力滞变形规律的翘曲位移函数.

Reissner［2］假定翼板纵向翘曲位移在横截面上符合二次抛物线的分布规律，首次运用能量变分法推导了矩形箱梁剪力滞控制微分方程并得到了其解析解.郭金琼等［3］认为横截面上的纵向位移差沿横向按三次抛物线分布，比较符合有限元分析和模型测验结果.Zhang等［4］从翼板面内剪切变形和弯曲剪流的分布规律上证明了二次抛物线翘曲位移模式分析剪力滞是合理的.许多学者对剪力滞翘曲位移函数的选取产生了争议，并进行了相关探讨和研究，提出了二次［2，4-7］、三次［3，8-10］、四次［10-11］、五次［10］抛物线、余弦曲线［12-14］、椭圆曲线及悬链线［10］、抽象函数［15］等多种形式的翘曲位移函数.目前对翘曲位移函数的选取仍然较为混乱.为了提高剪力滞效应分析的精确度，应用过程中对翘曲位移函数不断改进和修正，例如：He等［7］在剪力滞分析时引入腹板纵向位移实现轴向平衡的条件；钱寅泉等［12］以余弦曲线作为翘曲位移函数并考虑轴力平衡条件，在翘曲位移函数上附加全截面均匀位移；文献［4-5，8，12-14］对悬板和底板宽度、底板相对位置进行了修正，文献［4-5，12-14］选取板宽平方比为板宽修正系数，而文献［8］将面积比作为板宽修正系数；当悬板板宽与内侧顶板半宽相等时板宽修正系数消失，因此张元海等［16］通过试算的方法对悬板引入边界约束修正系数.此外，进行剪力滞效应分析时普遍的方法都是将剪切变形差函数作为翘曲广义位移，其物理意义不明确，而杨绿峰等［17］提出将剪力滞效应引起的附加挠度作为纵向翘曲广义位移，其物理意义更加明确.总之，目前还没有用于剪力滞效应分析的统一的翘曲位移函数表达式.

本文选取二次～五次抛物线、余弦曲线、悬链线等形式的翘曲位移函数，并引入板宽平方比、相对位置、悬板边界约束等系数对其修正.选用剪力滞引起的附加挠度并考虑翘曲应力需满足的自平衡条件来描述纵向翘曲位移，应用能量变分法建立剪力滞控制微分方程并求得附加挠度和翘曲应力解析解.通过算例分析剪力滞效应差异，为找出合理的用于剪力滞效应分析的翘曲位移函数提供参考.

1 剪力滞翘曲变形及应力

作用竖向任意分布荷载q（x）的箱梁如图1所示．坐标原点O位于截面形心处，y轴和z轴为横截面形心主轴；b为顶板半宽；α和β分别为悬板宽、底板半宽与顶板半宽的比值；h为顶、底板中面间的距离；zs和zx分别为y轴至顶、底板中面的距离；γ为zx与zs的比值．以剪力滞引起的附加挠度来描述纵向翘曲位移，能把剪力滞翘曲变形与初等梁弯曲变形分离开来．横截面上任意一点的纵向位移u（x，y，z）可表达为［16］

图1 梯形箱梁Fig．1 Trapezoidal box girder

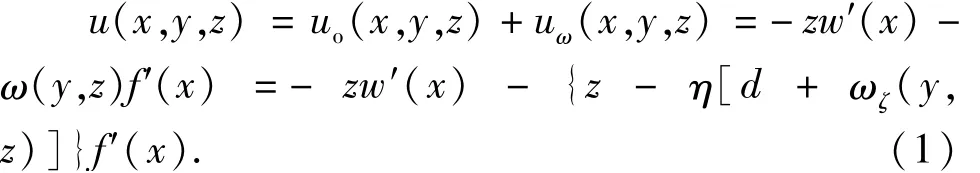
式中：uo（x，y，z）和uω（x，y，z）分别为横截面任意一点的初等梁纵向位移和纵向翘曲位移；w（x）为初等梁挠度；-w′（x）为初等梁挠曲转角；f（x）为剪力滞引起的附加挠度；-f′（x）为剪力滞引起的附加挠曲转角；ω（y，z）为剪力滞翘曲广义位移函数；ωζ（y，z）为箱梁各板的剪力滞翘曲位移函数；η和d为剪力滞翘曲应力不合成弯矩和轴力的自平衡修正系数．

由式（1）箱梁横截面上任意一点的纵向位移可得横截面上的应力为

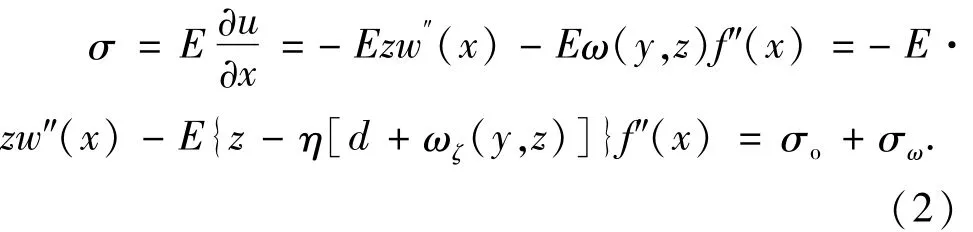
式中：σo和σω分别为初等梁弯曲应力和剪力滞翘曲应力，分别表达为

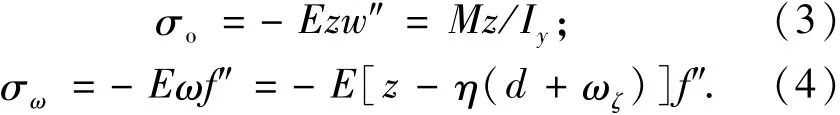
由式（1）和式（2）可以看出，引入剪力滞引起的附加挠度后，可将变形状态分解为初等梁弯曲变形和剪力滞翘曲变形，同时将总应力分解为初等梁弯曲应力和剪力滞翘曲应力，物理意义更加明晰，便于工程技术人员理解和应用.

与式（4）中剪力滞翘曲应力σω相对应的广义力矩Mω定义为

式中：Iω称为剪力滞广义翘曲惯性矩，Iω=∫A［z-

由式（4）和式（5），翘曲应力σω又可以表达为

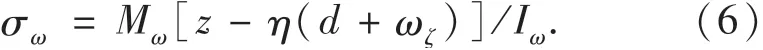
箱梁截面的翘曲应力需满足自平衡条件，即在箱梁横截面上不合成轴力和弯矩，则：

考虑y轴为形心主轴，将式（4）分别代入式（7）和式（8），可得

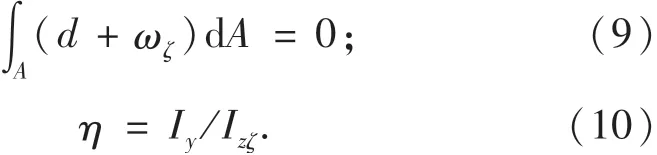
2 控制微分方程及其初参数解

综合薄壁箱梁的初等梁应变能、剪力滞翘曲应变能及外力势能，根据弹性力学的应变能计算公式，作用竖向分布荷载q（x）的箱梁的总势能表达为

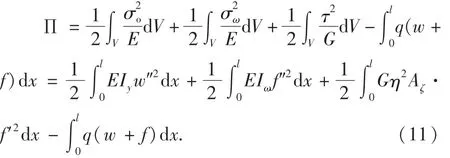
式中：k为Reissner参数

根据式（12）可以求出剪力滞附加挠度表达式为

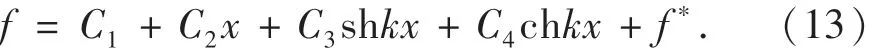
式中：C1～C4为积分常数，可由梁端边界条件确定；f*是与竖向分布荷载q（x）有关的特解．

求解积分常数的梁端边界条件为［5］

固定端：f=0，f′=0；

简支端：f=0，f″=0；

自由端：f″=0，f‴-k2f′=0．

为简化描述不同梁端支承的箱梁，文中用J-J箱梁、G-G箱梁、G-J箱梁、J-G箱梁分别表示两端简支、两端固定、左端固定右端简支、右端固定左端简支的箱梁.不同梁端支承箱梁承受的荷载如图2所示，采用初参数法［4］可导出图2中各箱梁的附加挠度计算公式.计算公式中：对于分别承受均布荷载q和集中荷载P的箱梁，其附加挠度分别用fq、fP表示；承受集中荷载的箱梁，其附加挠度计算公式中带有符号‖a的项表示x＞a时考虑此项.

对于图2（a）J-J箱梁，其附加挠度计算公式为

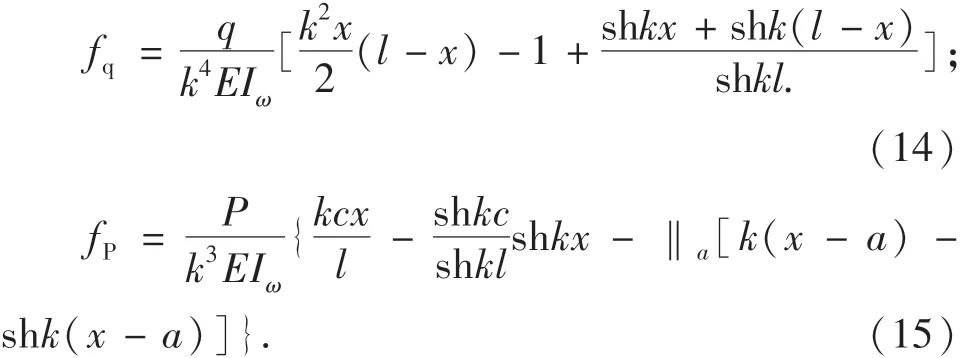
对于图2（b）G-G箱梁，其附加挠度计算公式为

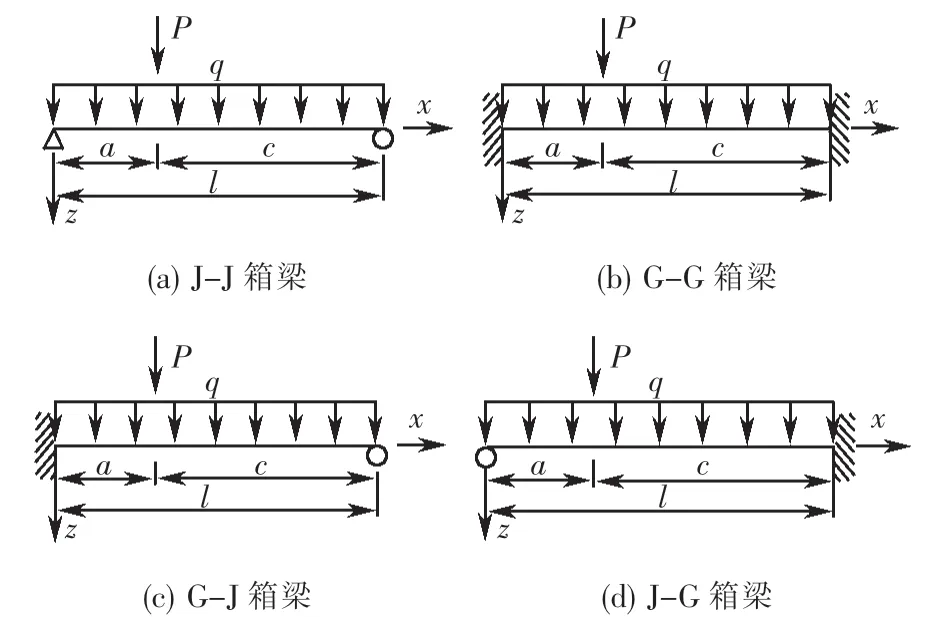
图2 不同梁端支承箱梁的荷载Fig．2 Load of different supported box girders

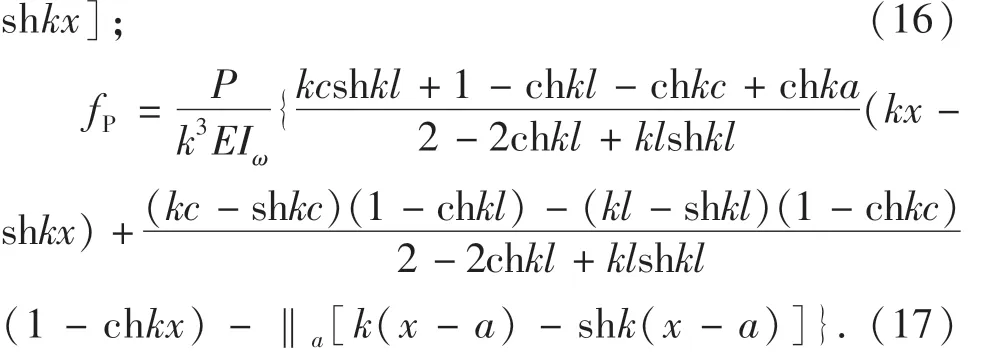
对于图2（c）G-J箱梁，其附加挠度计算公式为

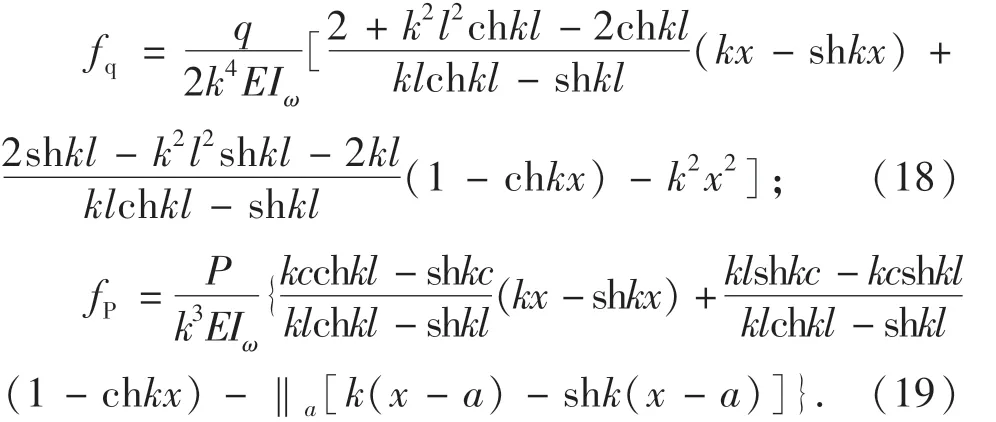
对于图2（d）J-G箱梁，其附加挠度计算公式为

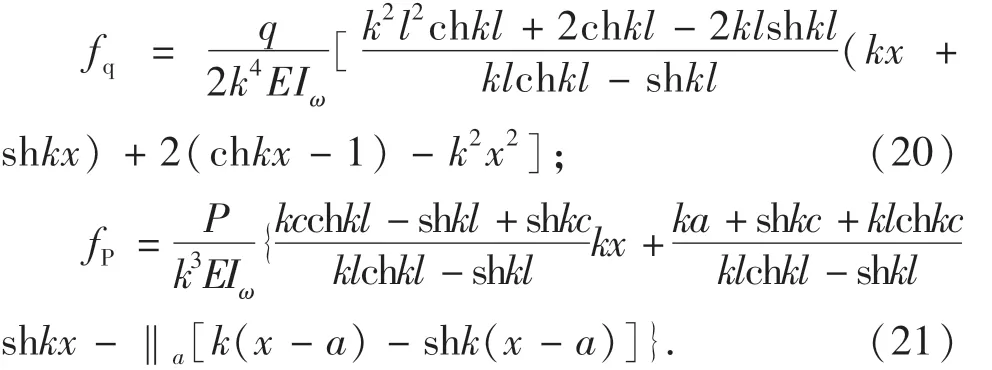
两跨连续箱梁可以分离出单跨J-G箱梁和单跨G-J箱梁计算，分离情况如图3所示.计算出了单跨箱梁的附加挠度，即得到连续箱梁的附加挠度.采用同样的方法，三跨连续箱梁可以分离出单跨J-G箱梁、G-G箱梁和G-J箱梁计算.

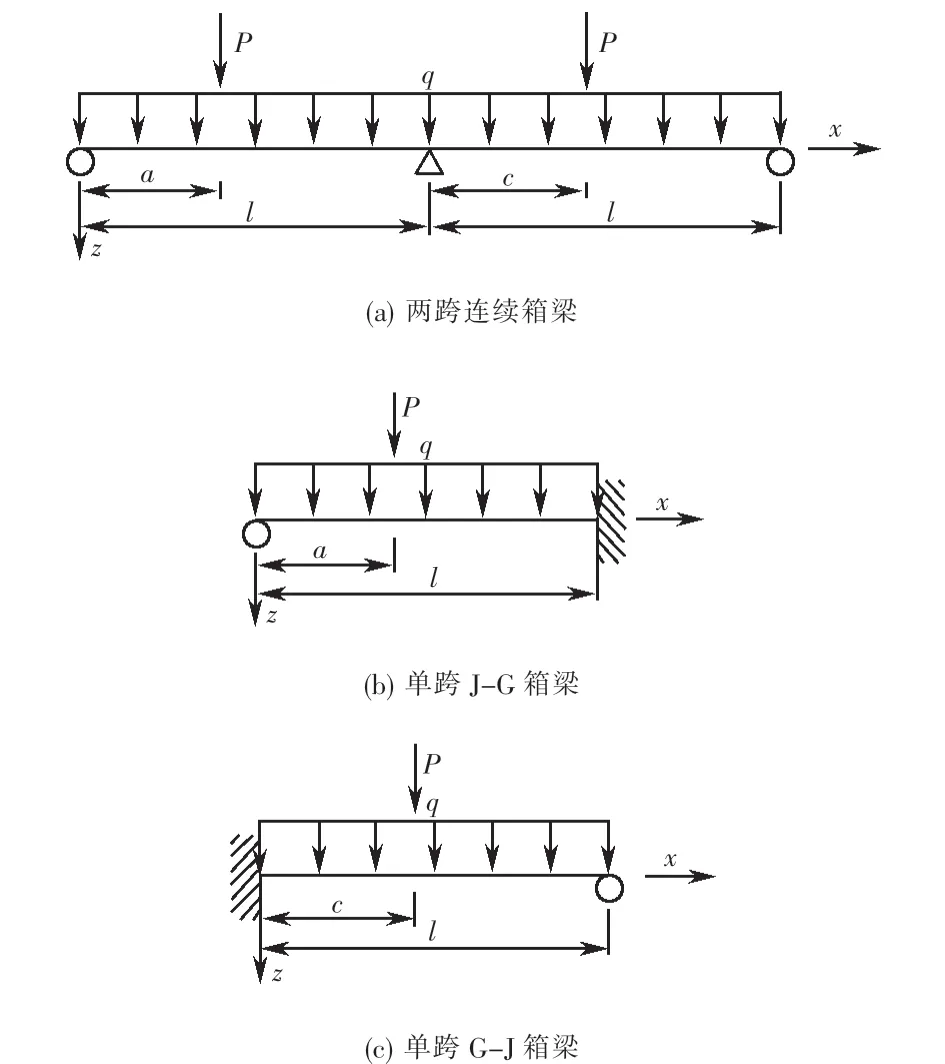
图3 两跨连续箱梁分离计算图Fig．3 Separate calculation of two-span continuous box girder

3 翘曲位移函数及几何特性求解

本文选取二次～五次抛物线、余弦曲线、悬链线等不同形式的翘曲位移函数，并对其引入板宽平方比、相对位置、悬板边界约束等修正系数.

抛物线型翘曲位移函数ωζ可表达如下（n分别取值为2、3、4、5）：

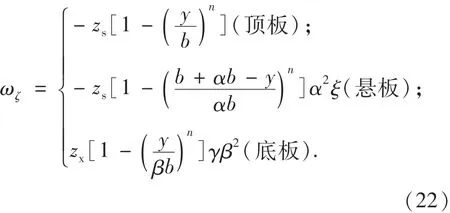
余弦曲线型翘曲位移函数ωζ为

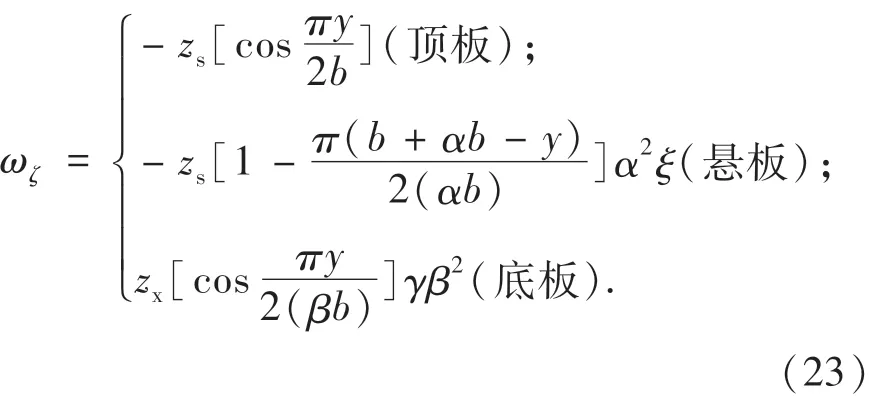
悬链线型翘曲位移函数ωζ为（参照文献［10］

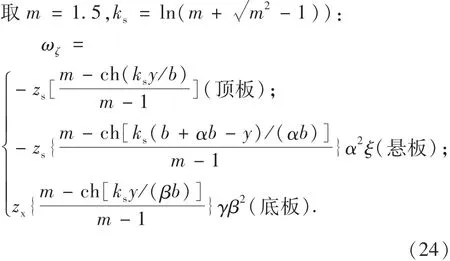
式（22）～式（24）中各参数的意义见图1，ξ为悬板边界约束修正系数，其值可取为1．4［13，16］．将式（22）～式（24）分别代入式（9），可得

根据Iζ、Izζ、Aζ的积分表达式，可得

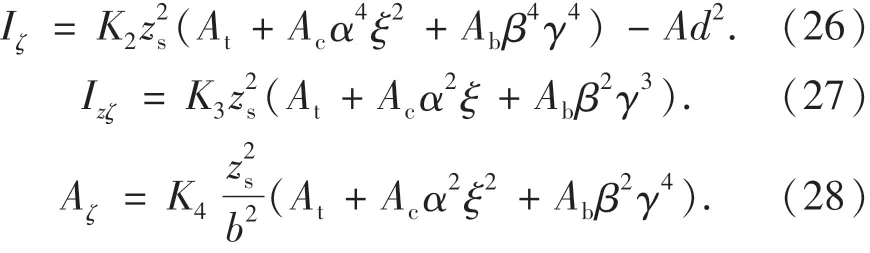
式中：A、At、Ac、Ab分别为箱梁的总横截面积、顶板截面积、两侧悬板截面积、底板截面积；K1～K4为几何特性系数．

不同翘曲位移函数的几何特性系数计算结果如表1所列.由表1可以看出几何特性系数K1～K4随抛物线次数增大而增大，二次抛物线、余弦曲线和悬链线的几何特性系数较为接近.

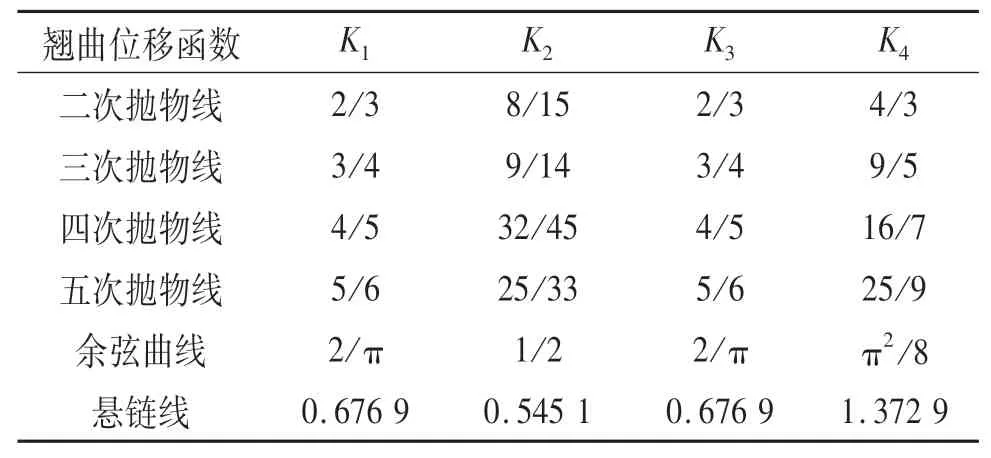
表1 几何特性系数Tab．1 Coefficients of geometric properties

4 算例分析及对比

选取简支箱梁和两跨连续箱梁等不同梁端支承的薄壁箱梁为算例，从截面应力和挠度两方面，分析不同翘曲位移函数对剪力滞效应的影响.

为描述按不同翘曲位移函数计算的截面应力与有限元解的总体吻合程度，引入均方根误差Re，Re越小表示截面应力与有限元解的总体吻合越好.有限元解是用ANSYS软件建立箱梁空间有限元模型求得，各板件用SHELL63壳单元模拟，腹板与顶底板间共节点连接，在支承处施加相应边界约束.

式中：σi为i点应力解析解；σAi为与i点对应的应力ANSYS解；N为计算点数，算例中在顶板半宽、悬板、底板半宽按10 mm间距均匀选取计算点．

4.1 算例1：简支箱梁

有机玻璃制作的简支箱梁模型［9］如图4所示，材料弹性模量E=3.0 GPa，泊松比μ=0.385.在跨中截面的顶板与腹板交接处作用总值P=272.2 N的对称集中荷载.采用ANSYS软件建立的简支箱梁有限元分析模型如图5所示，共划分3 362个节点，3 280个单元，在梁端底板节点施加约束，一端约束平动位移Ux、Uy、Uz和转角位移Rx、Rz，另一端约束平动位移Uy、Uz和转角位移Rx、Rz.

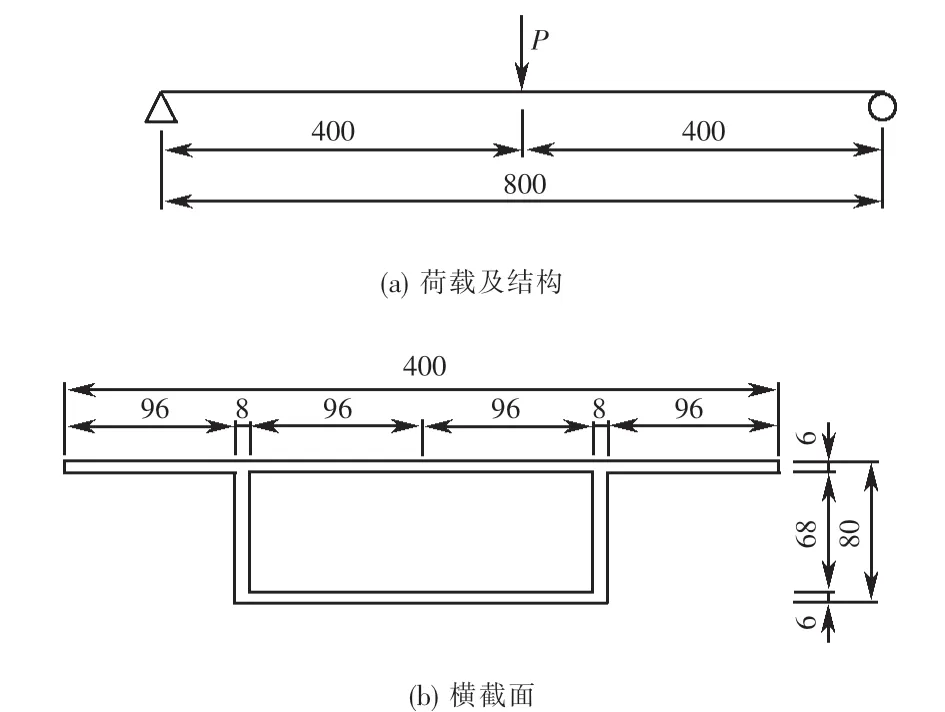
图4 简支箱梁（单位：mm）Fig．4 Simply supported box girder（unit：mm）

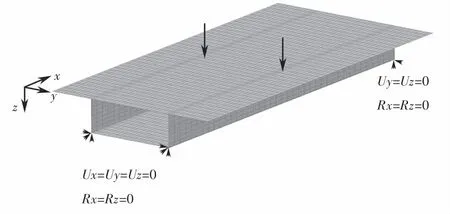
图5 简支箱梁有限元模型Fig．5 Finite element model of simply supported box girder

箱形梁各板件总应力为初等梁弯曲应力和剪力滞翘曲应力的叠加，由于剪力滞效应的影响，顶底板应力在横截面上分布不均匀，腹板与顶底板相交处出现峰值应力.简支箱梁跨中截面顶底板峰值应力及各板件应力总体误差分析结果如表2所列.由表2可以看出：按不同翘曲位移函数计算的顶底板峰值应力均与ANSYS解吻合良好，顶底板峰值应力与ANSYS解的偏差在-1.55%～7.49%（偏差是由不同翘曲位移函数计算的解析解与ANSYS解的差除以ANSYS解绝对值得出，表征解析解与ANSYS解的偏离程度）；顶板按二次抛物线计算的均方根误差最小，而底板按五次抛物线计算的最小，亦即此时与ANSYS解总体吻合最好，且顶板按二次抛物线、余弦曲线、悬链线计算的均方根误差很接近.

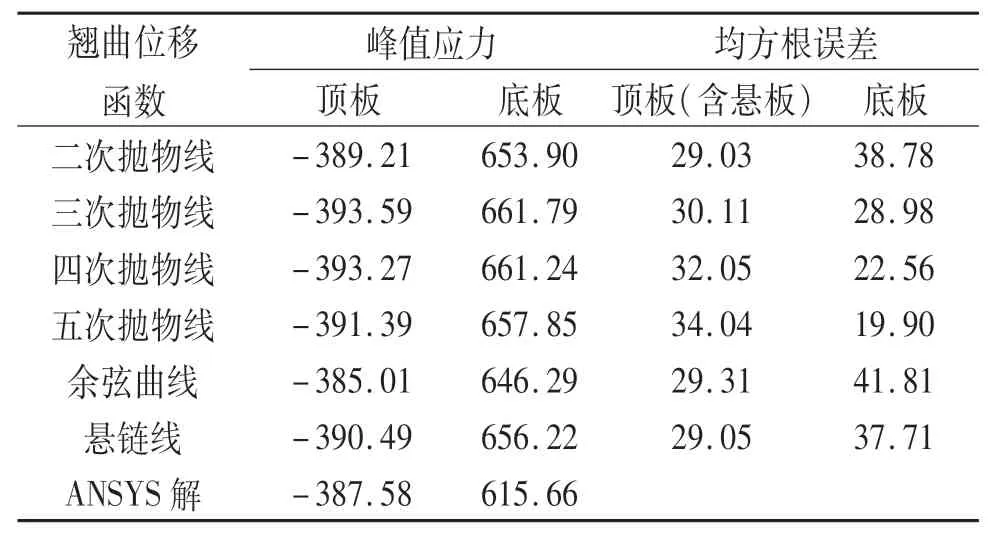
表2 跨中截面应力结果及误差分析Tab．2 Stresses and error analysis at mid-span cross section kPa

不同翘曲位移函数对挠度有一定的影响，简支箱梁的剪力滞附加挠度曲线如图6所示，跨中截面挠度结果如表3所列.由图6和表3可以看出：按不同翘曲位移函数计算的附加挠度差异明显，按五次抛物线计算的附加挠度最小，悬链线的最大且与二次抛物线的数值极为接近，最大值与最小值的比值为1.28；附加挠度约占初等梁挠度的10%，虽然附加挠度差异明显，计入初等梁挠度后的总挠度差异很小，总挠度最大值与最小值的偏差仅为2.26%.

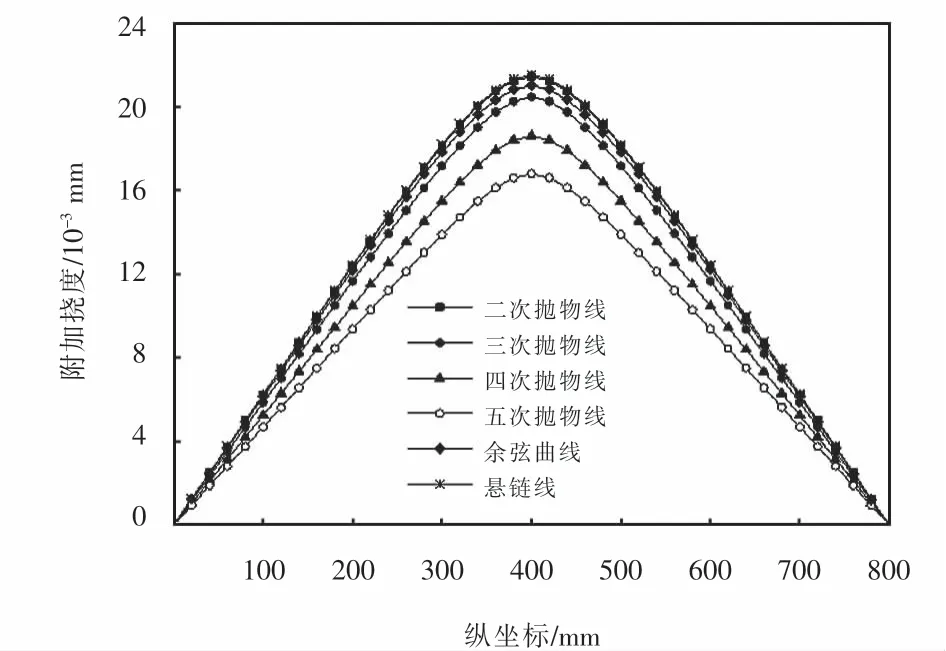
图6 简支箱梁剪力滞附加挠度曲线Fig．6 Additional deflection curves for shear lag of simply supported box girder

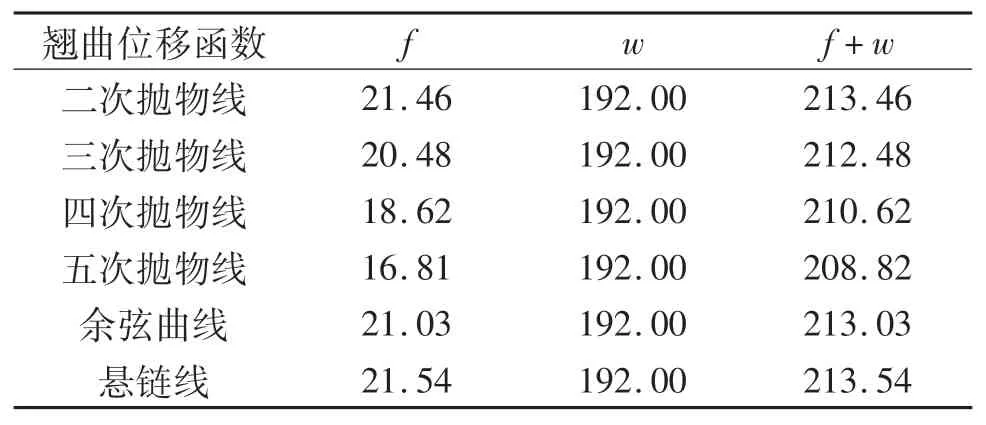
表3 跨中截面挠度Tab．3 Deflection at mid-span cross section 10-3 mm

4.2 算例2：两跨连续箱梁

有机玻璃制作的两跨连续箱梁模型［9］如图7所示，材料弹性模量E=2.8 GPa，泊松比μ=0.37.在跨中截面的顶板与腹板交接处作用总值P=20 N的对称集中荷载.采用ANSYS软件建立的两跨连续箱梁有限元分析模型如图8所示，共划分个5 346节点，5 280个单元，在底板节点施加约束，两侧梁端约束平动位移Uy、Uz和转角位移Rx、Rz，中支承处约束平动位移Ux、Uy、Uz和转角位移Rx、Rz.

图7 两跨连续箱梁（单位：mm）Fig．7 Two-span continuous box girder（unit：mm）

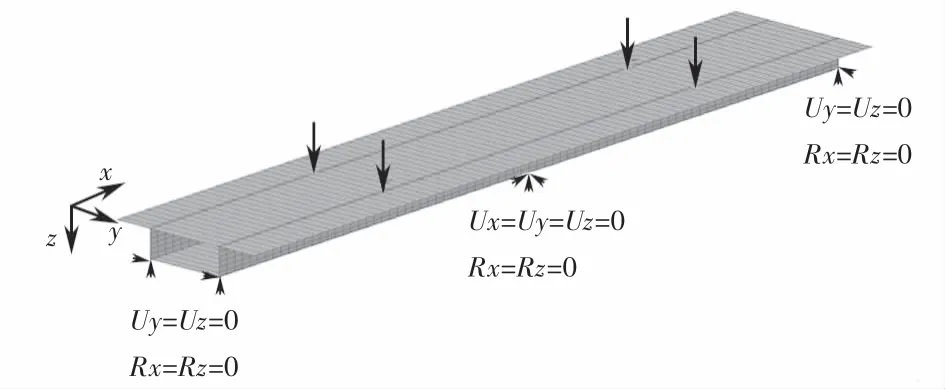
图8 连续箱梁有限元模型Fig．8 Finite element model of continuous box girder

两跨连续箱梁跨中截面和中支承截面的顶底板峰值应力及各板件应力总体误差分析结果如表4～5所列.由表4和表5可以看出：按不同翘曲位移函数计算的跨中截面和中支承截面顶底板峰值应力均与ANSYS解吻合良好，跨中截面顶底板峰值应力与ANSYS解的偏差为-2.39%～7.83%，中支承截面的偏差为-3.04%～4.01%；由均方根误差的结果可以看出，跨中截面的顶板按二次抛物线、底板按五次抛物线计算的应力与ANSYS解总体吻合最好，中支承截面的顶板按余弦曲线、底板按三次抛物线计算的应力与ANSYS解的总体吻合最好，顶板按二次抛物线、余弦曲线、悬链线计算的均方根误差很接近.

表4 跨中截面应力结果及误差分析Tab．4 Stresses and error analysis at mid-span cross section kPa

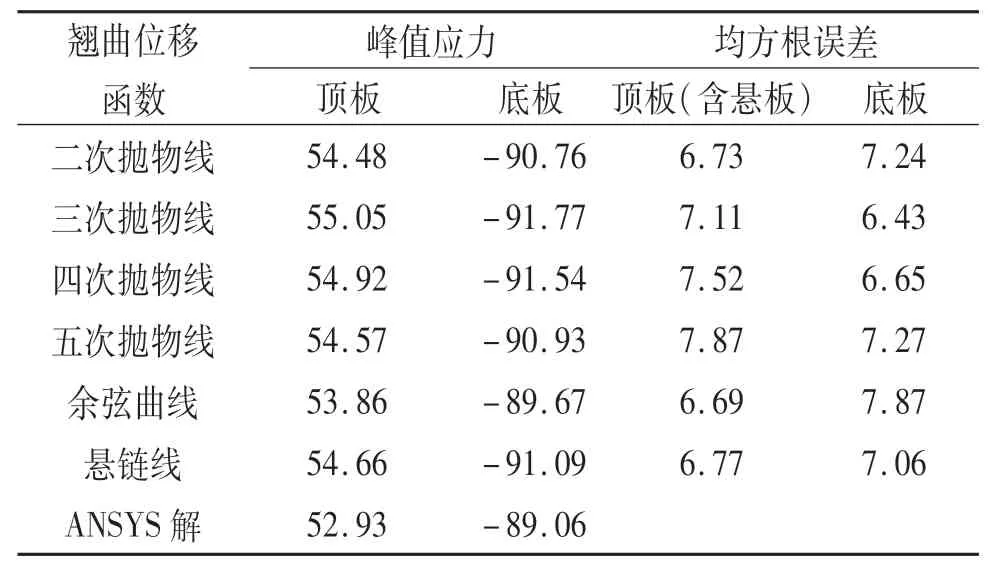
表5 中支承截面应力结果及误差分析Tab．5 Stresses and error analysis at mid-supported cross section kPa

两跨连续箱梁的剪力滞附加挠度曲线如图9所示，跨中截面挠度结果如表6所列.由图9和表6可以看出：按不同翘曲位移函数计算的附加挠度差异明显，按五次抛物线计算的附加挠度最小，悬链线的最大且与二次抛物线的数值极为接近，最大值与最小值的比值为1.26；附加挠度占初等梁挠度的12.38%～15.64%，虽然附加挠度差异明显，计入初等梁挠度后的总挠度差异很小，总挠度最大值与最小值的偏差仅为2.94%.

图9 连续箱梁剪力滞附加挠度曲线Fig．9 Additional deflection curves for shear lag continuous box girder

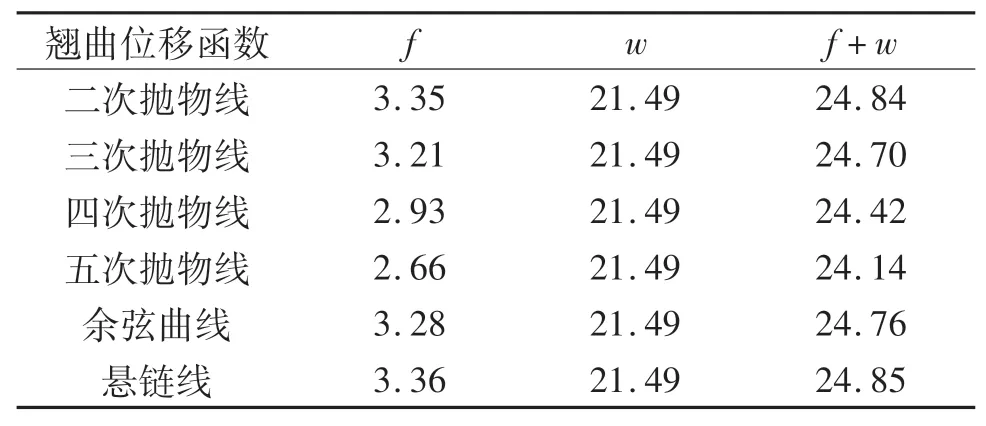
表6 跨中截面挠度Tab．6 Deflection at mid-span cross section 10-3 mm

5 结论

1）本文选取不同形式的翘曲位移函数，并考虑板宽平方比、相对位置、悬板边界约束等多参数修正，同时引入翘曲应力需满足的自平衡条件，以提高箱梁截面应力的计算精度.不同梁端支承的箱梁算例表明，按多参数修正的不同翘曲位移函数计算的顶底板峰值应力均与有限元解吻合良好.

2）均方根误差能够表征按不同翘曲位移函数计算的应力与有限元解的总体吻合程度，根据箱梁算例的均方根误差结果，顶板（含悬板）应力解析解建议采用二次抛物线、悬链线或余弦曲线计算，跨中截面和中支承截面的底板应力解析解建议分别采用五次抛物线、三次抛物线计算.

3）以剪力滞效应引起的附加挠度作为翘曲广义位移能够将剪力滞变形分离出来.剪力滞效应使跨中挠度增大，工程中不容忽视.按不同翘曲位移函数计算的附加挠度差异明显，最大值与最小值的比值达到1.28，但计入初等梁挠度后的总挠度差异却很小，总挠度最大值与最小值的偏差仅为2.94%.