基于前景理论的多灾点应急人员调度研究

刘康儒，朱昌锋*，王庆荣，张志伟，马 斌

（1.兰州交通大学 交通运输学院，兰州 730070；2.兰州交通大学 电子与信息工程学院，兰州 730070）

大规模突发事件初期，应急人员调度作为应急救援中最关键的环节之一，将直接影响到应急救援效率.因此，如何科学合理地调度应急人员是一个极具现实意义的课题.

国内外学者对应急人员调度问题已开展了一定的研究.文献［1-4］通过考虑救援时间不确定等灾情特征，以救援时间效用、救援效果和救援可靠性等为目标，构建了应急人员调度多目标优化模型.Rauchecker等［5］通过考虑救援单位间的协作，将救援单位调度描述为一个二元线性最小化问题.Chen等［6］从双边匹配的角度研究了志愿者派遣问题，提出了一种基于证据推理的方法来解决志愿者队伍与救援任务间的不确定匹配关系.然而，上述研究均未涉及多出救点-多受灾点-多应急任务下的应急人员调度问题，与现实存在偏差.针对上述不足，相关学者开始研究多受灾点背景下的应急人员调度问题.Zhang等［7］通过考虑救援队伍特征，构建了多阶段动态响应灾害链条件下的应急人员调度模型及算法.Li等［8］通过综合考虑应急人员的主观偏好和客观能力，构建了多受灾点背景下的应急人员调度模型.以上研究主要从时间效用和救援效果两个角度研究应急人员调度问题，但均以假设灾民和应急人员完全理性为前提.事实上，由于不完全不对称信息和不完美的判断能力的限制，灾民和应急人员对救援方案的心理感知是有限理性的.前景理论（prospect theory，PT）通过考虑现实中人的参照依赖和风险偏好等特征，真实描述了决策者的有限理性行为.文献［9-11］通过引入PT，刻画了有限理性条件下灾民对救援时间和需求满足率的心理感知.然而，上述研究均未考虑有限理性条件下应急人员对应急任务的心理感知.

基于上述分析，本文聚焦多受灾点下的应急人员调度问题，通过考虑灾民对救援到达时间和应急人员对应急任务的有限理性心理感知，构建以最大化时间满意度和任务胜任度为目标的应急人员调度多目标优化模型，并设计相应的第二代非支配排序的遗传算法（non-dominated sorting genetic algorithm II，NSGA-II）对模型进行求解.最后，通过算例求解与分析验证了本文模型和算法的合理性和有效性.

1 问题描述

假设某地发生大规模突发事件，受灾点和出救点集合分别为D=｛Dk｜k=1，2，…，n｝和A=｛Ai｜i=1，2，…，m｝．受灾点Dk的灾情严重程度为ρk，ρk越大，灾情越严重，0＜ρk≤1且．出救点Ai的应急小组数量为ai，出救点Ai的第j个应急小组为Pij．

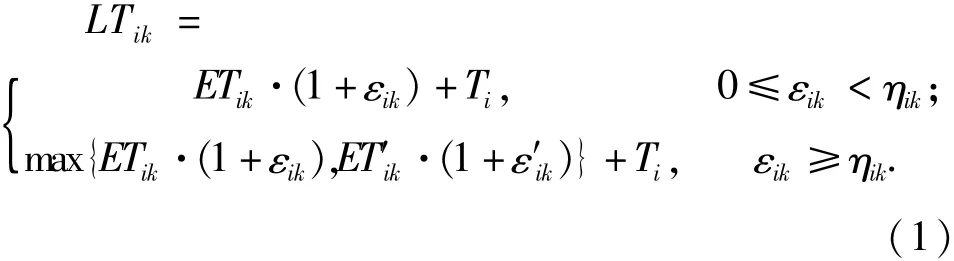
考虑到路况和天气等因素对救援到达时间的影响，将到达时间刻画为区间［ETik，LTik］．ETik为最短路径的理想到达时间，LTik为考虑路况、应急小组整备时间和更换路径条件下的最晚到达时间，即：其中：Ti为出救点Ai中应急小组的整备时间；εik为路况等因素对最短路径理想到达时间的影响系数，εik≥0；ET′ik为Ai至Dk备选路径的理想到达时间；ε′ik为路况等因素对备选路径理想到达时间的影响系数，ε′ik≥0；ηik为路径选择阈值．

对任务胜任度的衡量需综合考虑应急人员主观满意度和客观能力［8］．应急任务集合为TA=｛TAc｜c=1，2，…，C｝，受灾点Dk待完成任务的数量为Lk，Lk≤C．在主观满意度方面，应急小组Pij对应急任务TAc存在偏好序越小，应急小组Pij完成应急任务TAc的意愿越强，特别地表示Pij对应急任务TAc无意愿．在客观能力评价方面，应急任务TAc的能力指标权重集合为表示应急任务TAc关于第h个指标的权重且．出救点Ai中应急小组能力指标评价矩阵为为应急小组Pij的第h个能力指标的评价值的值以评分的形式给出，如0至10分．

xijk∈｛0，1｝表示应急小组Pij是否被派往受灾点Dk，为决策变量表示应急小组Pij是否被派往受灾点Dk完成任务TAc，为决策变量．

2 模型构建

2.1 有限理性下的时间满意度和任务胜任度

累积前景理论（cumulative prospect theory，CPT）是对PT的完善，其通过使用累积的而不是单独的决策权重，弥补了PT不满足随机占优和不适用于结果任意多的风险前景的缺陷.CPT主要通过价值函数和权重函数评价某一风险结果的价值.

2.1.1 时间满意度

对于不确定且结果任意多的到达时间，本文采用CPT刻画灾民对应急小组到达时间的满意度.时间满意度的价值函数如式（2）所示，价值函数曲线如图1所示.价值函数反映了有限理性下的灾民对时间价值的感知是基于参照点的，面对增益会规避风险，面对损失会追求风险，且对损失更敏感的心理.

图1 时间满意度的价值函数曲线Fig．1 Value function curve of time satisfaction

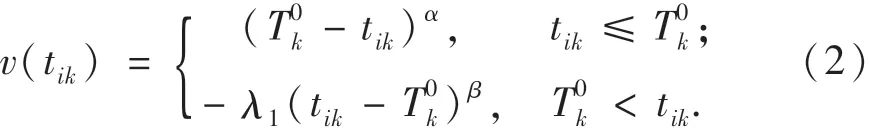
其中：α为风险规避参数，0＜α≤1；β为风险追求参数，0＜β≤1；λ1为灾民的损失规避系数，λ1≥1，根据既有研究的标定，α=β=0．88，λ1=2．25［12-14］；tik为出救点Ai中应急小组至受灾点Dk的实际到达时间，可取［ETik，LTik］中的任意时刻；T0k为受灾点Dk中灾民对救援到达时间的参照点，即：

记pik是与tik对应的概率，灾民感知收益和损失时的决策权重函数如式（4）所示，决策权重函数曲线如图2所示.决策权重函数反映了有限理性条件下的灾民会迷恋小概率事件的心理.

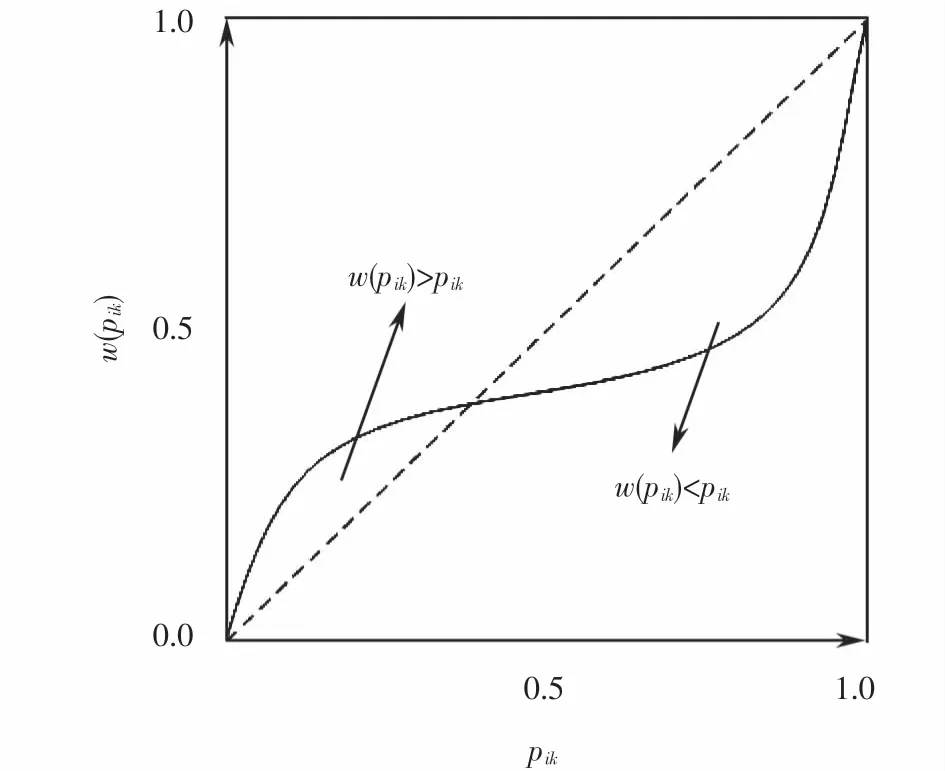
图2 时间满意度的决策权重函数曲线Fig．2 Decision weight function curve of time satisfaction

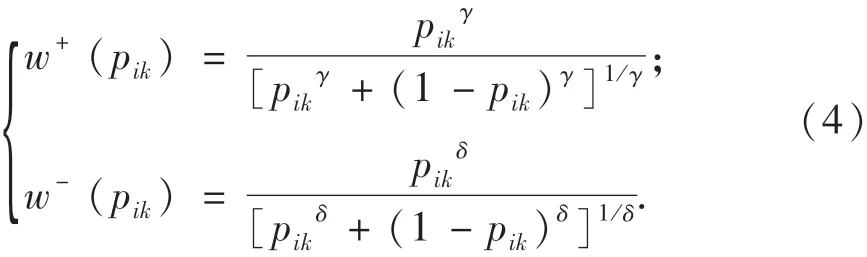
其中：γ为获得感知概率参数，γ＞0；δ为损失感知概率参数，δ＞0．根据既有研究的标定，γ=0．61，δ=0．69［12-14］．

假设有M+N+1种可能的到达时间，将连续的到达时间区间［ETik，LTik］离散化为K段为第g段中值对应的概率［12-13］，则灾民感知收益和损失时的累积权重函数为

在价值函数和累积权重函数的基础上，灾民对应急小组Pij调往Dk的时间满意度为

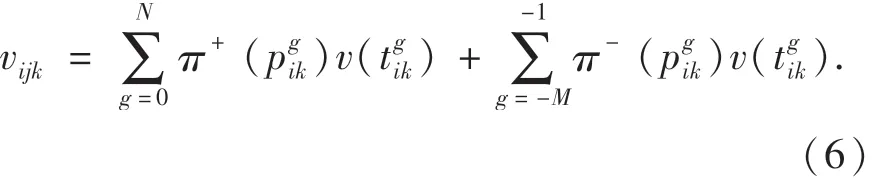
2．1．2 任务胜任度

任务胜任度是应急小组主观满意度和客观能力的结合［8］．对于不同的应急任务，应急小组主观满意度的变化并非是线性的，且应急小组会对应急任务存在有限理性的心理感知．因此，基于应急小组对应急任务的偏好序，本文采用CPT的价值函数刻画应急小组Pij对应急任务TAc的主观满意度S（rc ij），即：

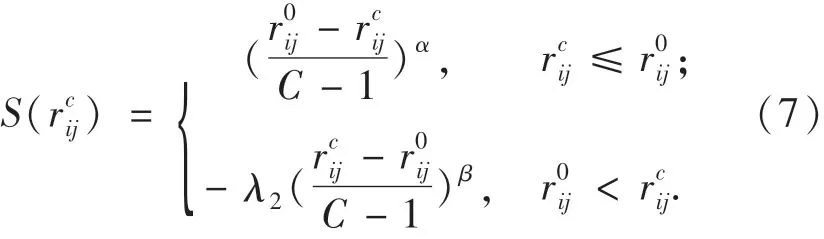
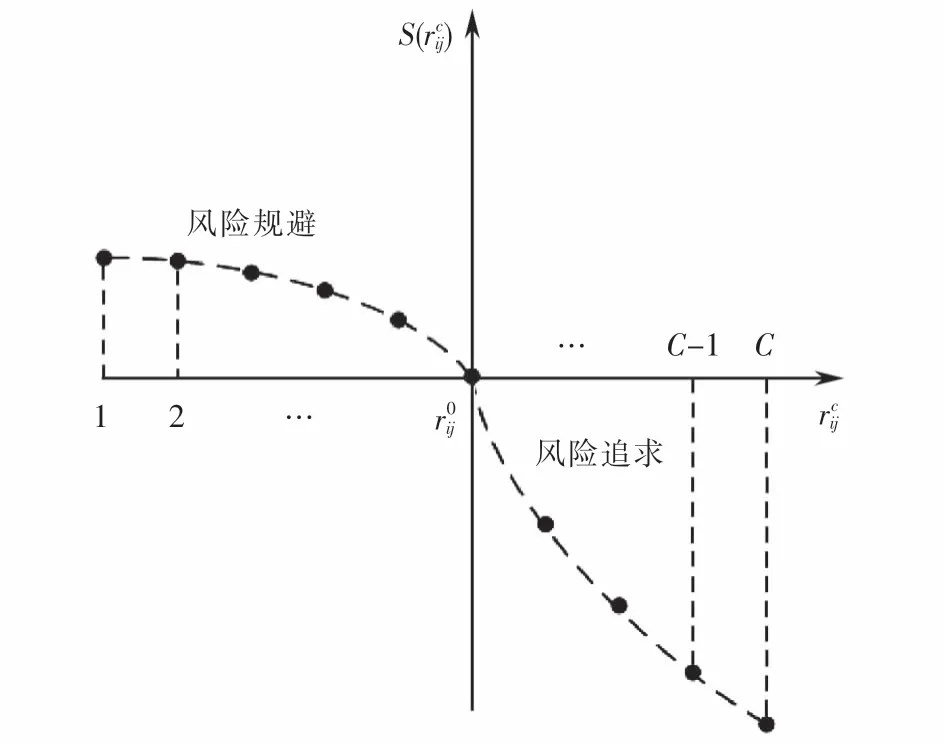
图3 应急小组主观满意度函数曲线Fig．3 Subjective satisfaction function curve of emergency team

在应急小组主观满意度和客观能力的基础上，采用几何平均算子得出Pij完成任务TAc的胜任度即：

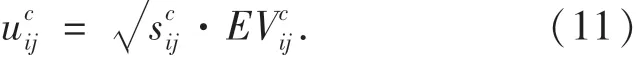
2．2 应急人员调度模型构建

基于2．1节内容，结合应急人员调度实际，有限理性条件下考虑多受灾点的应急人员调度模型如下：其中：式（12）和（13）分别为时间满意度和任务胜任度目标函数；式（14）表示一个应急小组只能去往一个受灾点；式（15）表示一个应急小组只能完成一项应急任务；式（16）为出救点Ai中应急小组的数量约束；式（17）和（18）为决策变量取值约束．

3 算法设计

3.1 胜任度求解策略

通过分析式（12）～（18）可发现，受灾点Dk的任务胜任度的计算是一个以效益最大为目标的广义最优指派问题．对此，匈牙利算法可在多项式时间内求解该类问题，且应用广泛．另外，根据总应急小组数与总应急任务数间的不确定关系，应急人员调度存在三种情景.基于上述分析，本文在匈牙利算法的基础上，提出了一种适应不同应急人员调度情景的任务胜任度求解策略，如表1所列.

表1 胜任度求解策略Tab．1 Competency solving strategy

3.2 多目标优化算法设计

在所建模型和胜任度求解策略的基础上，应急小组调度方案的确定具有明显的并行性，遗传算法的群体适应度评价和随机搜索等特征使其具备求解该类问题的优势［15-16］.对于多目标优化，NSGA-II算法在继承遗传算法的全局并行搜索优势的同时，通过提出快速非支配排序算子、拥挤比较算子和精英策略提高了Pareto前沿的精确性、均匀性和收敛性［17-18］.本文采用NSGA-II算法对应急小组调度模型进行求解，下面是NSGA-II算法的关键操作.

图4 任务数额增加方法Fig．4 Method of increasing the number of tasks

1）染色体编码

分析式（12）～（18）和胜任度求解策略可知，仅有决策变量xijk参与染色体编码，故染色体编码采用二进制编码．整条染色体可划分为个基因片段，每个片段的基因位数等于受灾点数n．具体地，某一基因片段的第k个基因位的值表示：若该基因片段所指的应急小组被派往受灾点Dk，则该基因片段第k个基因位的值为1，否则为0．染色体长度为，染色体编码示意图如图5所示.

图5 二进制编码染色体Fig．5 The binary coded chromosome

2）约束处理方式及适应度函数的确定

在胜任度求解策略的基础上，考虑到模型约束的复杂性不强，故将约束（14）～（18）直接加入到新个体的生成过程中，如个体初始化，交叉和变异等操作.另外，采用目标函数作为适应度函数，即：

3）交叉，变异算子

基于图5所示二进制编码染色体，本文采用单点交叉和单点变异算子.其中，交叉算子的交叉位置指向两个相邻基因片段的连接处，变异算子的变异位置指向任一基因片段.以三个受灾点，三个出救点，每个出救点中有一个应急小组为例，交叉和变异算子分别如图6～7所示.

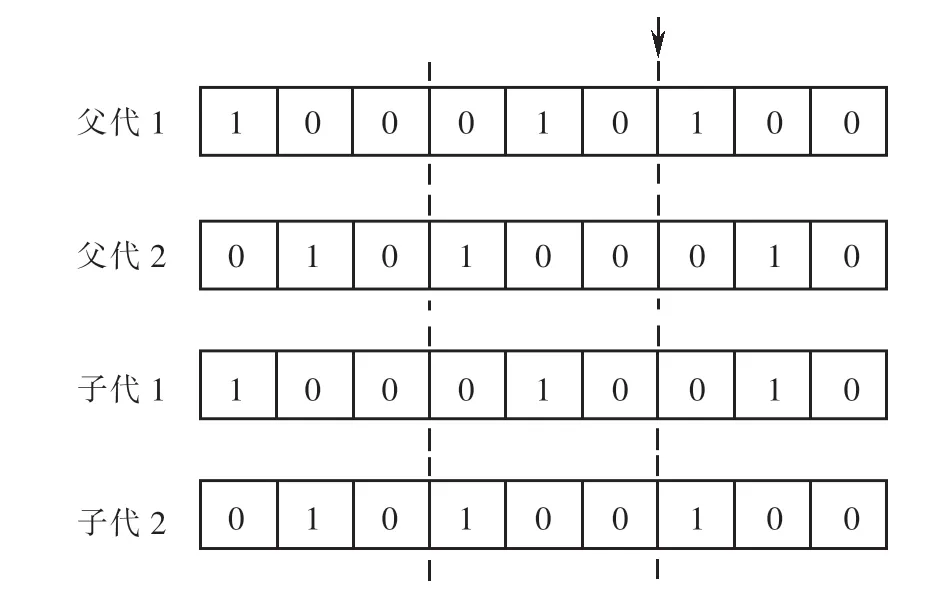
图6 交叉算子Fig．6 Crossover operator

在确定算法关键操作的基础上，算法流程如图8所示.

图8 NSGA-II算法流程Fig．8 NSGA-II algorithm flow

Pareto前沿解集在提供多个可选方案的同时，也为决策者做出最终决策带来了困难.在决策者没有明显偏好且应急决策时间紧迫的情况下，给出理想解筛选方法是有必要的.结合本研究内容，本文采用文献［7］中的理想解筛选方法.

4 算例分析

4.1 算例背景

考虑到三种胜任度求解策略的应用情景最终都可转化为情景Ⅱ，因此，为验证模型和算法的合理性，本文在情景Ⅱ的基础上设计算例，并对其进行求解与讨论分析.

图7 变异算子Fig．7 Mutation operator

算例由4个受灾点，5个出救点和5类应急任务构成.各灾点灾情严重程度分别为ρ1=0．35，ρ2=0．2，ρ3=0．2，ρ4=0．25．各出救点中应急小组数量分别为a1=3，a2=2，a3=4，a4=3，a5=4，依照出救点的顺序，各应急小组的任务偏好参照点为｛3，3，4，4，3，3，3，2，2，3，3，3，3，3，4，4｝．应急小组能力评价指标共7项．各出救点应急小组整备时间分别为T1=1，T2=1．5，T3=2，T4=1．5，T5=1.5.各受灾点的最短路径理想到达时间如表2所列；路况等因素对最短路径理想到达时间的影响系数如表3所列；各受灾点的应急任务如表4所列；应急任务指标权重如表5所列；应急小组对应急任务的偏好序如表6所列；应急小组能力指标评价值如表7所列.

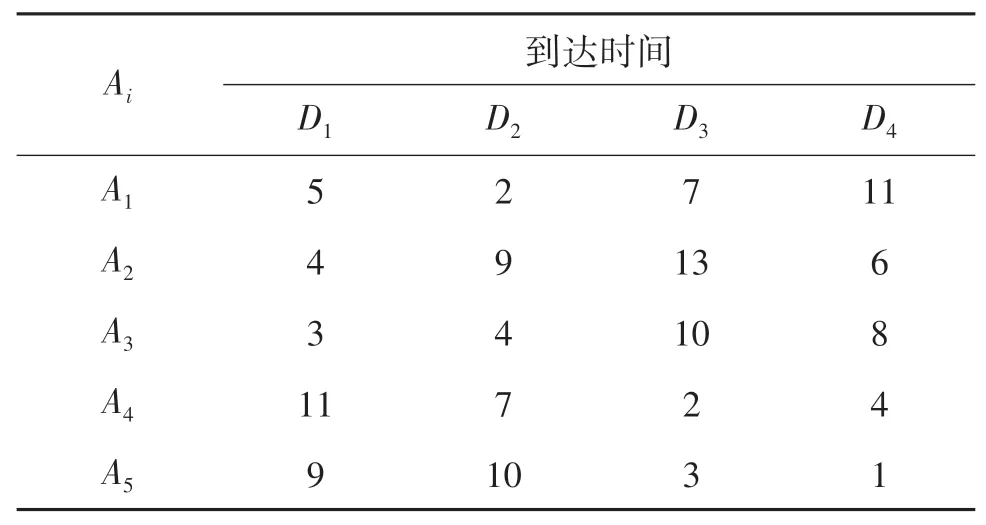
表2 理想到达时间Tab．2 Ideal arrival time h

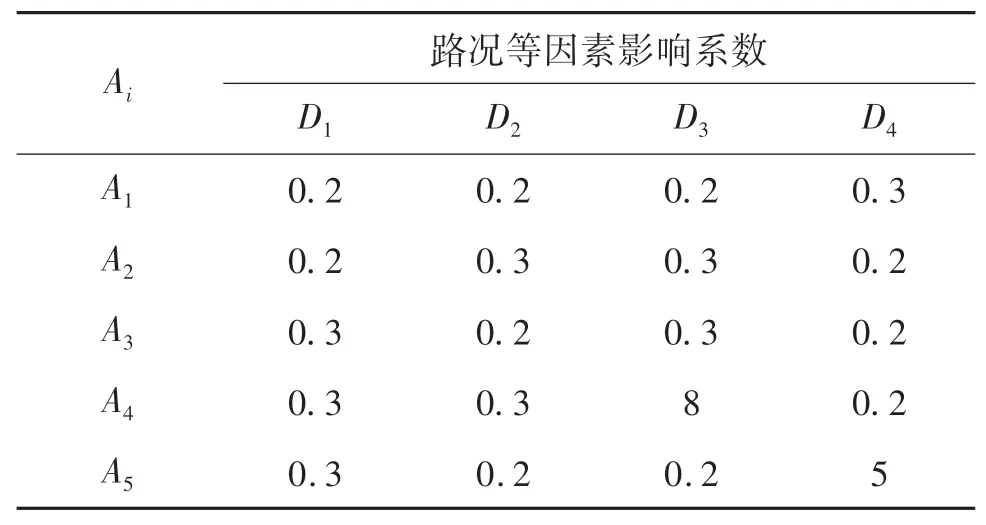
表3 路况等因素对理想到达时间的影响系数Tab．3 Influence coefficient of road conditions and other factors on ideal arrival time

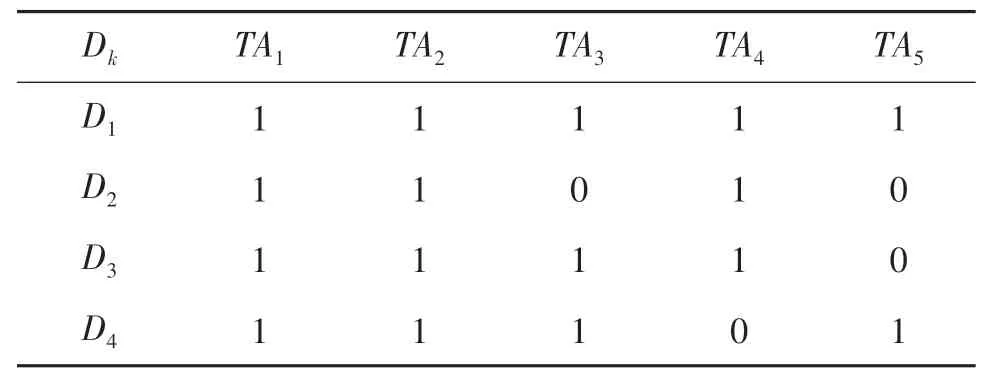
表4 各受灾点待完成的应急任务Tab．4 Emergency tasks at each disaster area

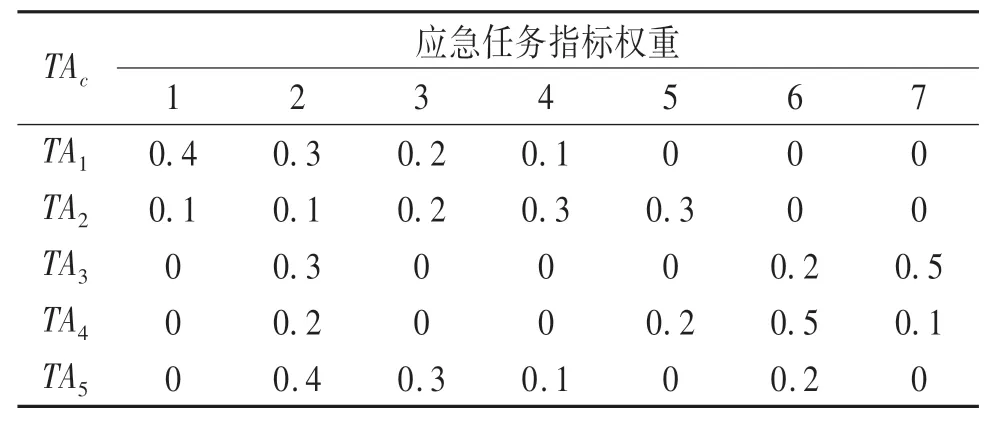
表5 应急任务指标权重Tab．5 Emergency task indicator weight

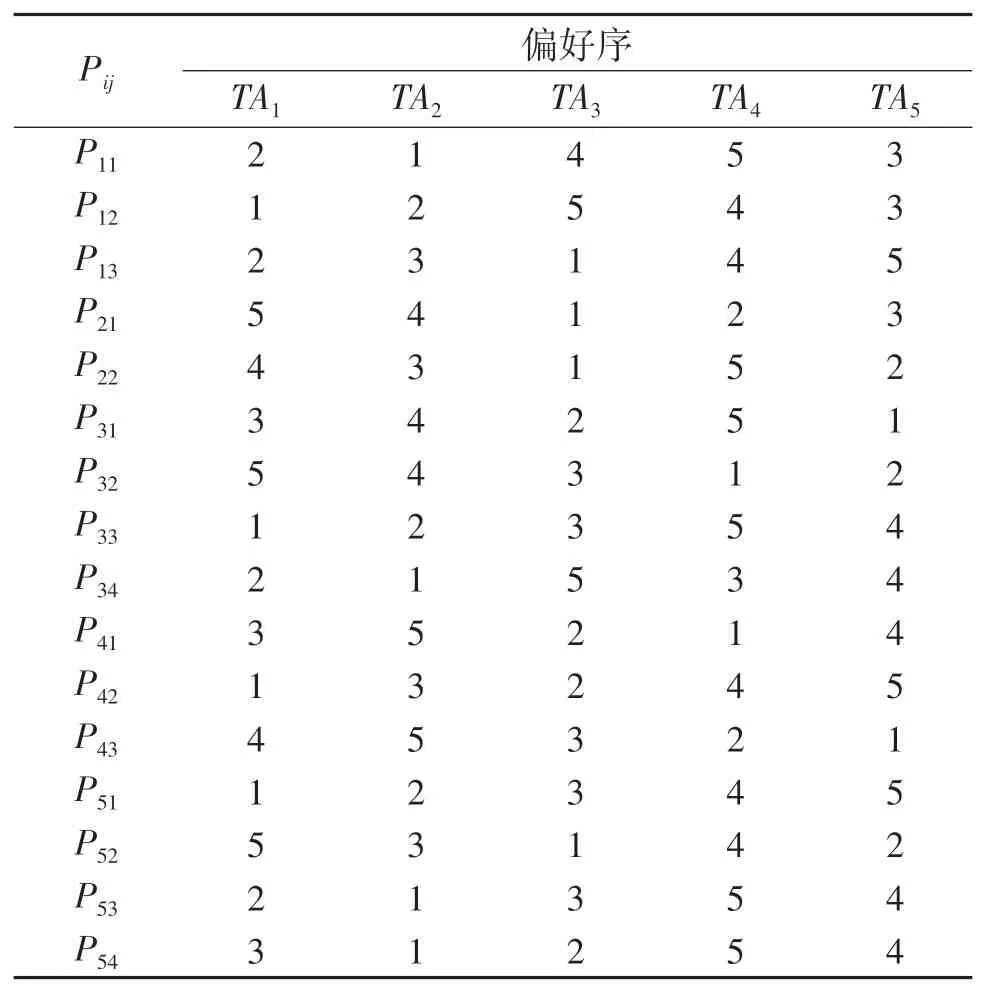
表6 应急小组偏好序Tab．6 Emergency team preference

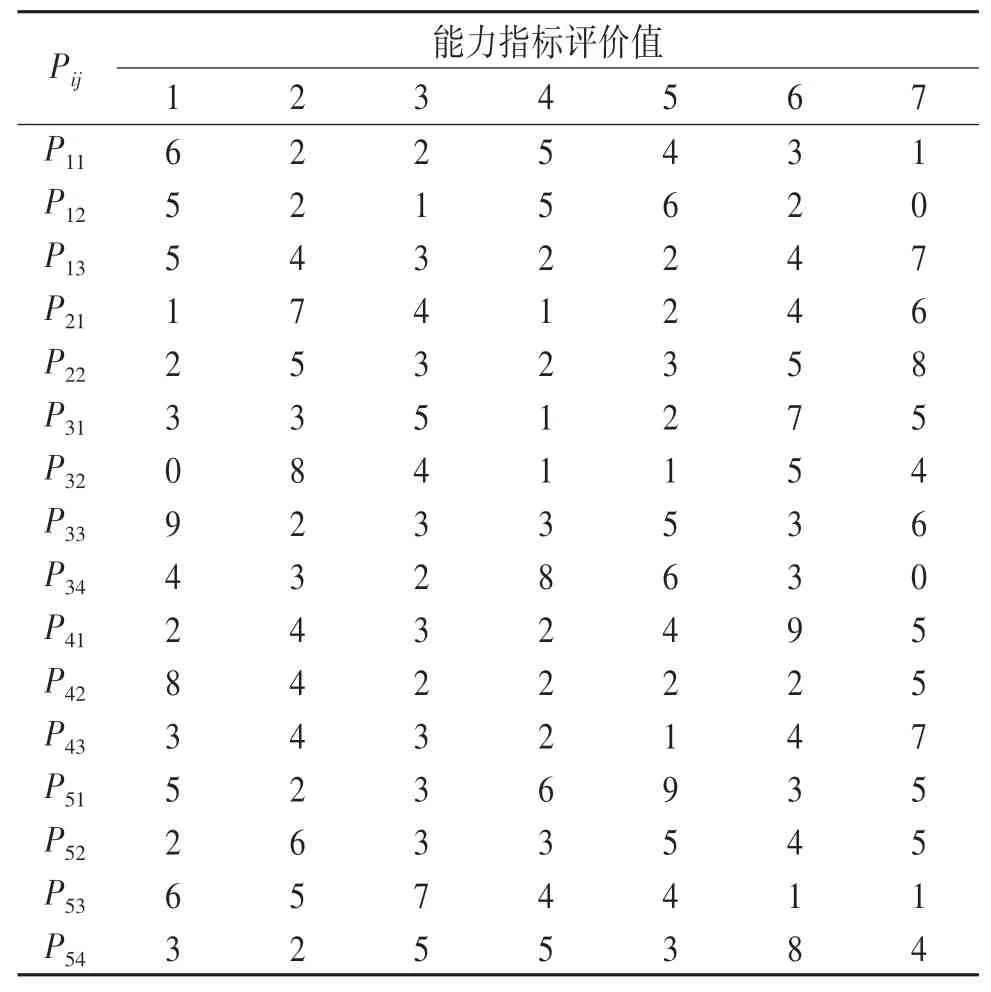
表7 应急小组能力指标评价值Tab．7 Evaluation value of emergency team capability index分

基于给定的基础数据，应急小组对各项应急任务的胜任度如表8所列.

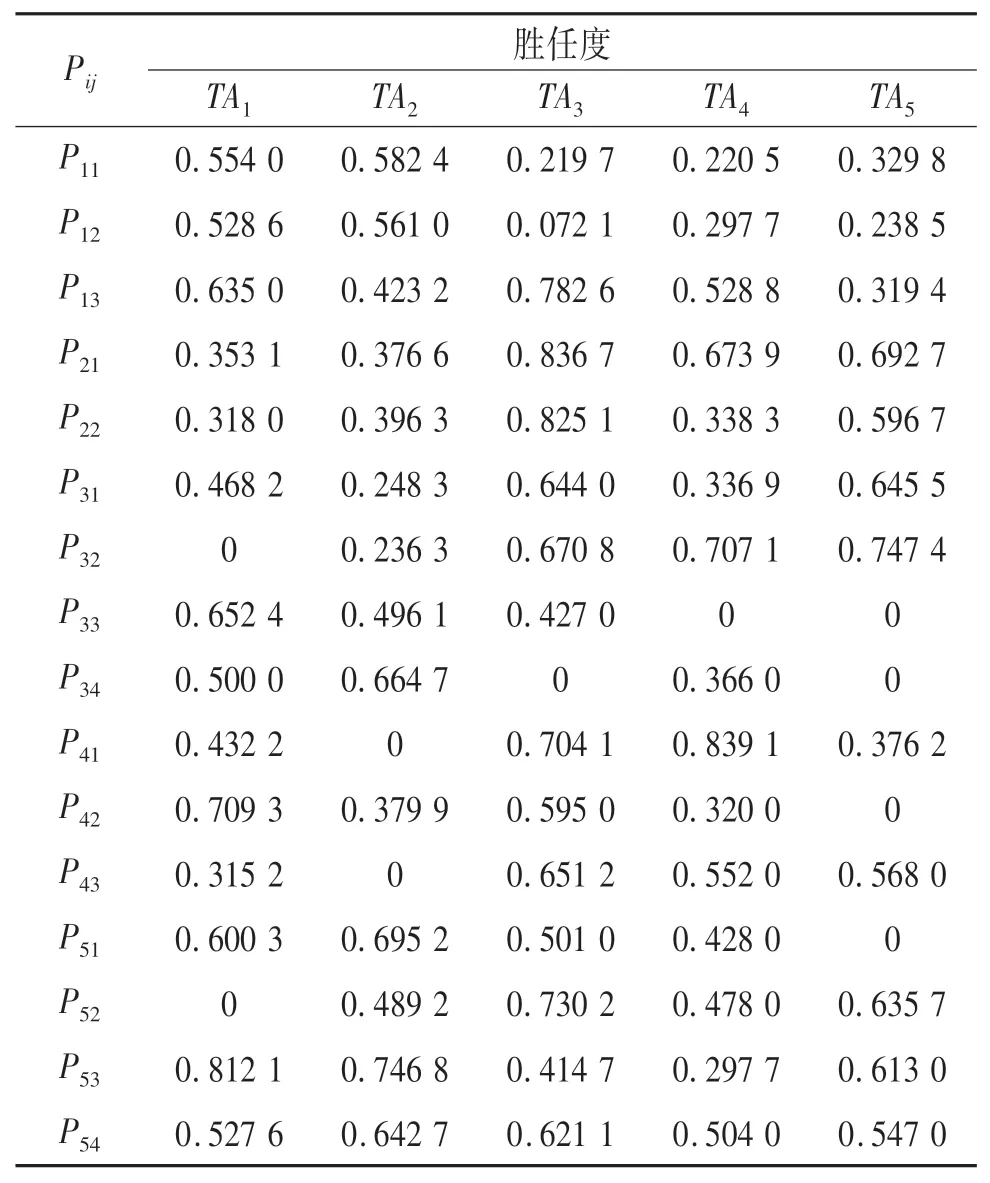
表8 应急小组任务胜任度Tab．8 Emergency team task competence

4.2 算例求解与分析

本文基于VisualStudio2017开发环境，采用C++编程语言实现算法并求解算例.在算法方面，设置种群规模为100，迭代次数maxGen为500次，交叉概率pc为0．9，变异概率pm为0．02．在模型参数方面，设置λ1=λ2=2.25.Pareto前沿解数的迭代曲线如图9所示.

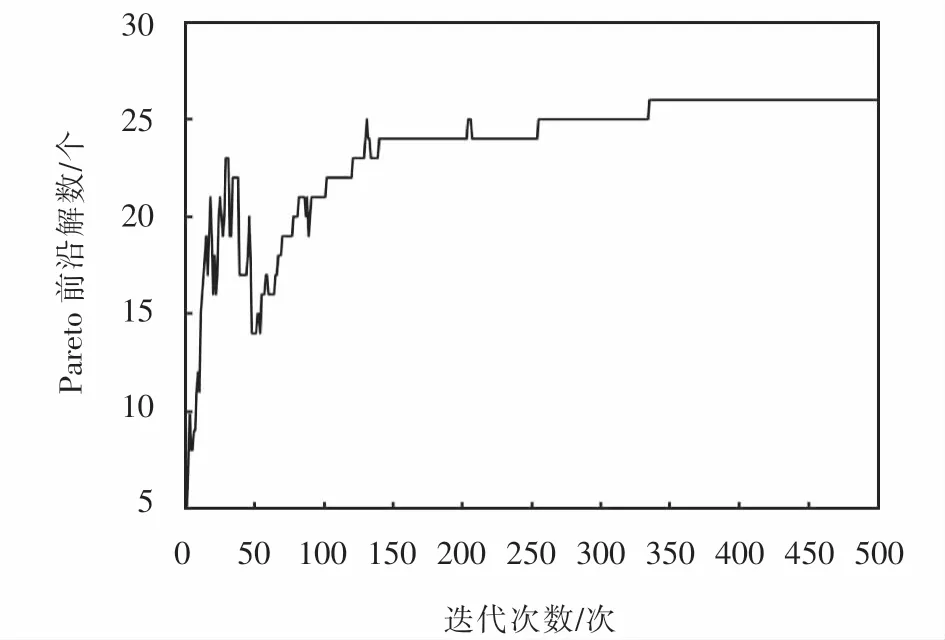
图9 Pareto前沿解数的迭代曲线Fig．9 Number iteration curve of Pareto frontier solutions

由图9可见，当算法迭代350次左右时，Pareto前沿解的数量收敛到26个.为进一步验证迭代350次的Pareto前沿已经收敛，将迭代350次和500次的Pareto前沿进行对比，如图10所示.

图10 迭代350次与500次的Pareto前沿Fig．10 Pareto frontier with 350 and 500 iterations

由图10可以看出，一方面，迭代350次和500次的Pareto前沿基本一致，这表明迭代350次的Pareto前沿已经收敛.基于以上分析可得，针对多受灾点条件下的应急人员调度问题，设计的NSGA-II算法是有效的，可快速准确地收敛.另一方面，时间满意度和任务胜任度间存在负相关关系：随着救援时间的增加，任务胜任度先快速增加后趋于稳定，这是目标间的冲突造成的.

取迭代350次的Pareto前沿解集做进一步的分析，选择时间满意度最优解（方案1）、理想解（方案2）和任务胜任度最优解（方案3）作为研究对象.三个特殊解对应的目标函数值和具体调度方案如表9～10所列.

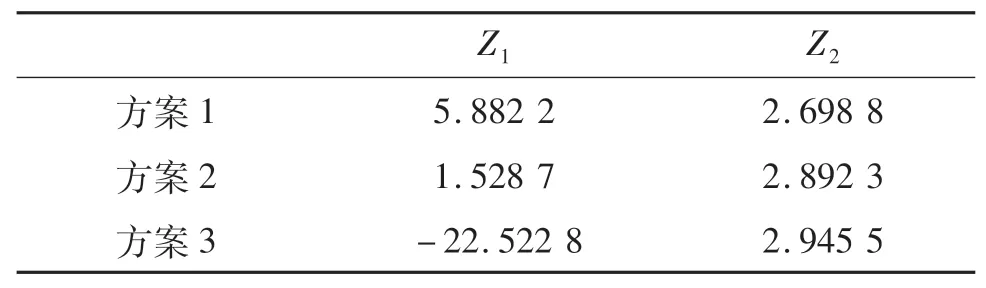
表9 三个特殊解的目标函数值Tab．9 Objective function values for three special solutions

首先，综合表2、表3和表10可以看出，在方案2中，A4和A5中部分应急小组被派往因严重受路况等因素影响而在到达时间上明显劣势的受灾点.这说明，严重受路况等因素影响的理想到达时间较短的路径已成为制约救援效果提升的瓶颈，决策者须予以重视.其次，记应急小组胜任度最高的任务为1级任务，次高任务为2级任务，以此类推.为了验证胜任度求解策略的合理性，我们给出了应急小组完成不同胜任度等级任务的数量分布，如图11所示.

由图11可以看出，方案2与方案3在任务分配效果上差异较小，方案1与另外两个方案的任务分配效果差异较大.然而，结合表8和表10可发现，三个方案中各受灾点的任务分配都是基于当前所得应急小组的最优分配.这说明，在所建模型的基础上，胜任度求解策略兼顾了模型求解优化和高质量的任务分配.最后，考虑到应急救援初期的时间紧迫性，结合图10，本文推荐在时间满意度处于［1.528 7，5.882 2］的调度方案中选择最优方案.

表10 三个特殊解的具体调度方案Tab．10 Specific scheduling schemes for three special solutions

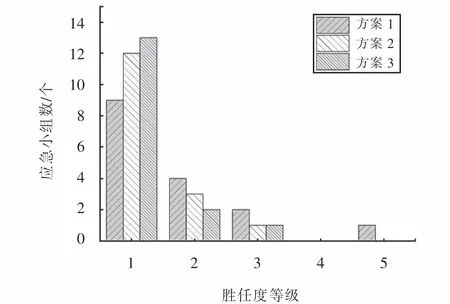
图11 不同胜任度等级下的小组数分布Fig．11 Distribution of team numbers under different competency levels

4.3 前景理论参数分析

4.3.1 时间满意度参数分析

时间满意度主要会受到风险态度参数α，β和感知概率参数γ，δ的影响．为分析时间满意度对α，β，γ，δ的灵敏度，以三个方案的时间满意度为研究对象进行分析，如图12所示.

图12 参数α，β，γ，δ对三个方案的时间满意度的影响Fig．12 The influence of parametersα，β，γ，δon the time satisfaction of the three schemes

由图12（a），12（b），12（c）可看出：时间满意度与α呈正相关，与β呈负相关；方案1的时间满意度对α的敏感度远大于β，方案2的时间满意度对α和β的敏感度相当，方案3的时间满意度对β的敏感度远大于α．考虑到三个方案下的灾民对救援时间的感知分别为高增益、混合低增益和高损失，上述现象表明：当救援时间整体早于灾民预期时，灾民更倾向于为保留当前增益而规避风险；当救援时间整体晚于灾民预期时，灾民更倾向于追求增益而规避风险；当救援时间整体略早于灾民预期时，灾民在有规避风险倾向的同时，也会存在为追求更大增益而追求风险的倾向．这有助于促进方案的优化调整．另外，整体来看，时间满意度对β的敏感度更强，这符合获取信息有限（对救援到达时间的不确定性考虑不足）的灾民会对救援时间有过高期望且对损失更敏感的现实.

由图12（d），12（e），12（f）可看出：时间满意度与γ呈正相关，与δ呈负相关；方案1的时间满意度对γ的敏感度远大于δ，方案2的时间满意度对γ和δ的敏感度相近，方案3的时间满意度对δ的敏感度远大于γ。这是因为，γ越大，灾民越倾向于感知方案在时间上较优，故方案1和方案2中处于增益状态的灾民的时间满意度越大，方案3的灾民处于高损失状态，故几乎不受γ的影响．对δ的分析与γ类似．另外，整体来看，时间满意度受δ的影响更大，这说明灾民会对方案无效更敏感.

4.3.2 任务胜任度参数分析

任务胜任度主要会受到风险态度参数α，β的影响．我们以三个方案的任务胜任度为研究对象，分析其对风险态度参数α，β的灵敏度，如图13所示.

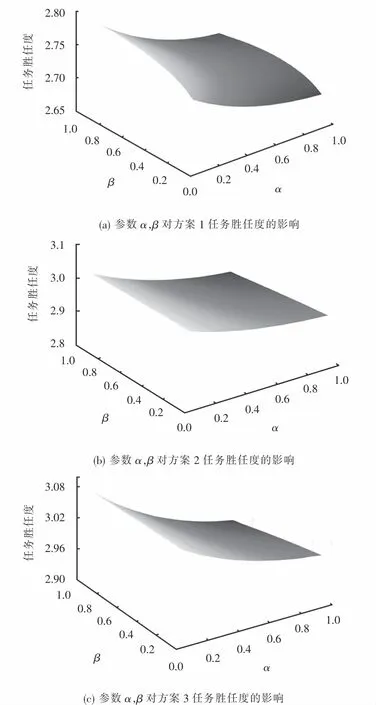
图13 参数α和β对三个方案的任务胜任度的影响Fig．13 Influence of parametersαandβon task competency of three schemes

由图13可看出：任务胜任度在整体上与α呈负相关，与β呈正相关；三个方案均对α更敏感.这说明三个方案在任务胜任度上均是较优的，故任务偏好得到满足的应急人员会更倾向于为保留当前增益而规避风险.同时，该现象符合在救援时间紧迫的背景下，应急人员会对任务偏好序期望较低的现实.

5 结论

1）构建的多目标优化模型结合胜任度求解策略，可得到一系列Pareto前沿解供决策者依据具体灾情选择，可为多受灾点下的应急人员调度及相关研究提供参考.

2）设计的NSGA-II算法可快速、准确地求出Pareto前沿，是解决本文目标问题的有效手段.

3）引入前景理论刻画的时间满意度和任务胜任度，真实地反映了应急救援中灾民和应急人员的心理感知，有效弥补了既有研究完全理性人假设的不足.

4）考虑灾情动态性和应急小组的不完全偏好序是下一步研究重点.