基于融合神经网络的短期交通流预测研究

李 杰，张子辰，孟凡熙，朱 玮

（长安大学 电子与控制工程学院，西安 710064）

短期交通流预测是智能交通系统的重要技术基础，建立高精度的短期交通流预测模型，对于交通管理与规划、缓解交通拥堵和提高交通效率具有重要意义.文献［1］针对短时交通流数据的非线性和随机性特点，为提高其预测精度，提出了一种基于自适应最稀疏窄带分解（adaptive sparsest narrow-band decomposition，ASNBD）和复合多尺度模糊熵（composite multiscale fuzzy entropy，CMFE）的短时交通流数据特征信息提取方法，试验结果表明，该方法可以有效提取短期交通流中的特征信息，进而提高预测精度；文献［2］将扩展Kalman滤波算法应用于高速公路交通流模型中，并讨论了该模型在一条具有3个等长路段的公路的应用，对该路段车流密度、车流速度进行跟踪，仿真结果证明了该算法具有很高的实用性；文献［3］建立了一种基于张量分解的算法，实现了短期交通流数据的建模预测；文献［4］提出了一种基于支持的短期交通流预测模型，并运用该模型对指定地点及其邻域内的交通流数据进行建模分析；文献［5］提出了一种基于褪色卡尔曼滤波的算法，对蓝牙采集到的交通流数据进行预测实验.以上模型结构简单且计算方便，但是针对高度非线性、不稳定的交通序列难以达到较好的效果，且模型抗干扰能力有待提高.

近年来，随着数学理论的发展和深度学习的崛起，越来越多的学者将深度学习应用于交通流预测领域中.文献［6］提出了一种深度全连接神经网络模型，对短期交通流时间序列进行预测，并通过参数调整，提高了预测精度；文献［7］提出了一种基于图卷积网络的深度学习模型，对车速和车流量数据进行了建模预测；文献［8］提出了一种时空深度张量神经网络模型（spatial-temporal deep tensor neural networks，ST-DTNN）来捕获网络交通流数据中的时间维、空间维和深度维特征信息，形成融合路段传输模型和深度学习的城市路网短时交通流预测模型，实验证明，该模型相对于基准模型预测精度更高，且具备模拟演化机理方面的优势；文献［9］提出了一种基于时空图卷积循环神经网络（spatiotemporal graph-convolutional recurrent neural network，STG-CRNN）的短期交通流预测模型，将时空图作为预测模型的输入，采用图卷积获取交通流数据空间依赖关系，采用门控循环神经网络获取交通流数据的时空依赖关系，在美国公共数据集中进行验证，实验结果表明，该模型在平均绝对误差、均方根误差、平均绝对百分比误差上均优于其他竞争模型；文献［10］提出了基于注意力机制和1DCNN-LSTM（convolutional neural networks-long short-term memory）网络的短时交通流预测模型，该模型结合了CNN（convolutional neural networks）的时间扩展和LSTM（long short-term memory，LSTM）的长时记忆的优点，提高了交通流的预测精度；文献［11］提出了一种多组分时空跨域神经网络模型，该模型采用Conv-LSTM（convolutional neural networks-long short-term memory）或Conv-GRU（convolutional neural networks-gated recurrent unit）对多种数据进行建模，将模型与时间戳特征嵌入、多个跨域数据融合相结合，并与其他模型共同辅助模型进行流量预测.以上研究虽然显示出了更快的收敛速度和更强的鲁棒性，但是面对非平稳性和非线性极强的交通流序列，预测精度仍有待提高.

经验模态分解（empirical mode decomposition，EMD）能够将交通流信号分解成多个固有模态分量，使得由多个特征影响的复杂序列被分解为由单一特征影响的信号，从而提高交通流序列的平稳性［12］，易于分析和建模，但其缺点在于多个特征尺度的信号在同一个模态分量中出现，使得冗杂信号被引入各个模态分量，出现模态混叠现象［13］.相对于LSTM，双向长短期记忆网络（bidirectional long short-term memory，BiLSTM）的优点在于从正向和反向同时读取输入序列［14］，使得模型可以更充分的学习交通流序列中的时间关系，提高模型的预测精度.此外，注意力机制（attention mechanism，AM）能够进一步捕捉对于整个时间序列更加有影响力的时间点，并对其分配更高的训练权重，提高递归模型的特征提取能力［15］.因此，本文针对车道占用率序列，提出了一种基于集成经验模态分解（ensenmble empirical mode decomposition，EEMD）和BiLSTM的深度神经网络学习模型，并将AM融入神经网络中，为递归网络序列中的神经元分配权重，对短期交通流序列预测进行研究.

1 车道占用率数据及其集成经验模态分解

1.1 车道占用率序列

本文采用车道占用率描述交通流信息.车道占用率是交通流预测中的一个重要参数，其描述了某一时间段内车辆通过一截面的时间占该段时间的百分比，其表示如下：

其中；Rt表示t时间段内车道占用率；tT为总观测时间；ti为第i辆车的占用时间；n为该路段的车辆数．

PeMS（california transportation agency performance measurement system，PeMS）数据集是加州交通运输局测量系统采用39 000个独立探测器实时采集的交通流数据，这些传感器跨域了加州所有主要城市的高速公路系统.PeMSD-SF（performance measurement system dataset-san francisco）数据集是PeMS数据集的一个子数据集，它是旧金山海湾地区高速公路的车道占用率的测量数据.本文重点研究其中一个探测器所采集的从2008年3月6日至2008年4月3日的车道占用率，其探测器位置如图1所示.数据每10 min采样一次，每天的数据序列中样本数为144个，总的样本数为4 032个.本文取其中前三周作为训练集，后一周作为测试集.由于偶然因素，所测得的交通流数据会存在少量异常值.本文使用统计学方法中的3σ原则筛选滤除异常值，然后取异常点附近的10个采样值的均值来填补该异常点.

图1 探测器位置Fig．1 Detector position

1.2 经验模态分解

经验模态分解是一种自适应信号时频处理方法，被广泛应用于非线性非平稳的复杂信号.该方法可以自适应地将原始信号分解成一系列固有模态函数（intrinsic mode function，IMF），所分解出来的各IMF分量包含了原信号的不同时间尺度的局部特征，满足下式：

其中：X（t）表示原始信号；m（t）表示原始信号上包络线与下包络线的均值信号；Res表示停止分解时的残余分量.将测试集中7天的车道占用率序列使用EMD方法进行分解，得到IMF1～IMF10和Res信号，如图2所示.EMD方法可将复杂的车道占用率信号分解成多个平稳的分量信号，但是由于不同特征尺度的信号在一个IMF分量中出现，或者同一个特征尺度的信号被分散到不同的IMF分量中，会出现模态混叠现象.

图2 EMD分解结果Fig．2 Results of EMD decomposition

1.3 集成经验模态分解

集成经验模态分解作为EMD方法的一种改进形式，解决了EMD方法中出现的模态混叠现象，即通过在分解的过程中多次引入均匀分布的白噪声抑制信号本身的噪声，从而得到更加精准的上下包络线，同时对分解结果进行平均处理，平均处理次数越多，噪声给分解带来的影响就越小［16］.EEMD的分解流程和分解结果分别如图3和图4所示.

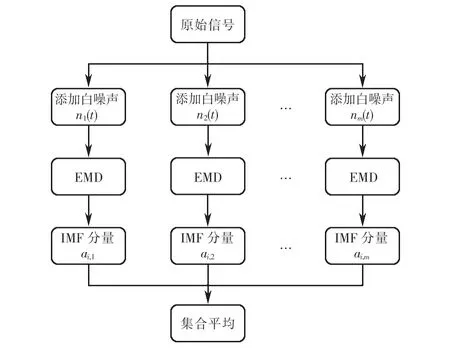
图3 EEMD流程图Fig．3 Flowchart of EEMD

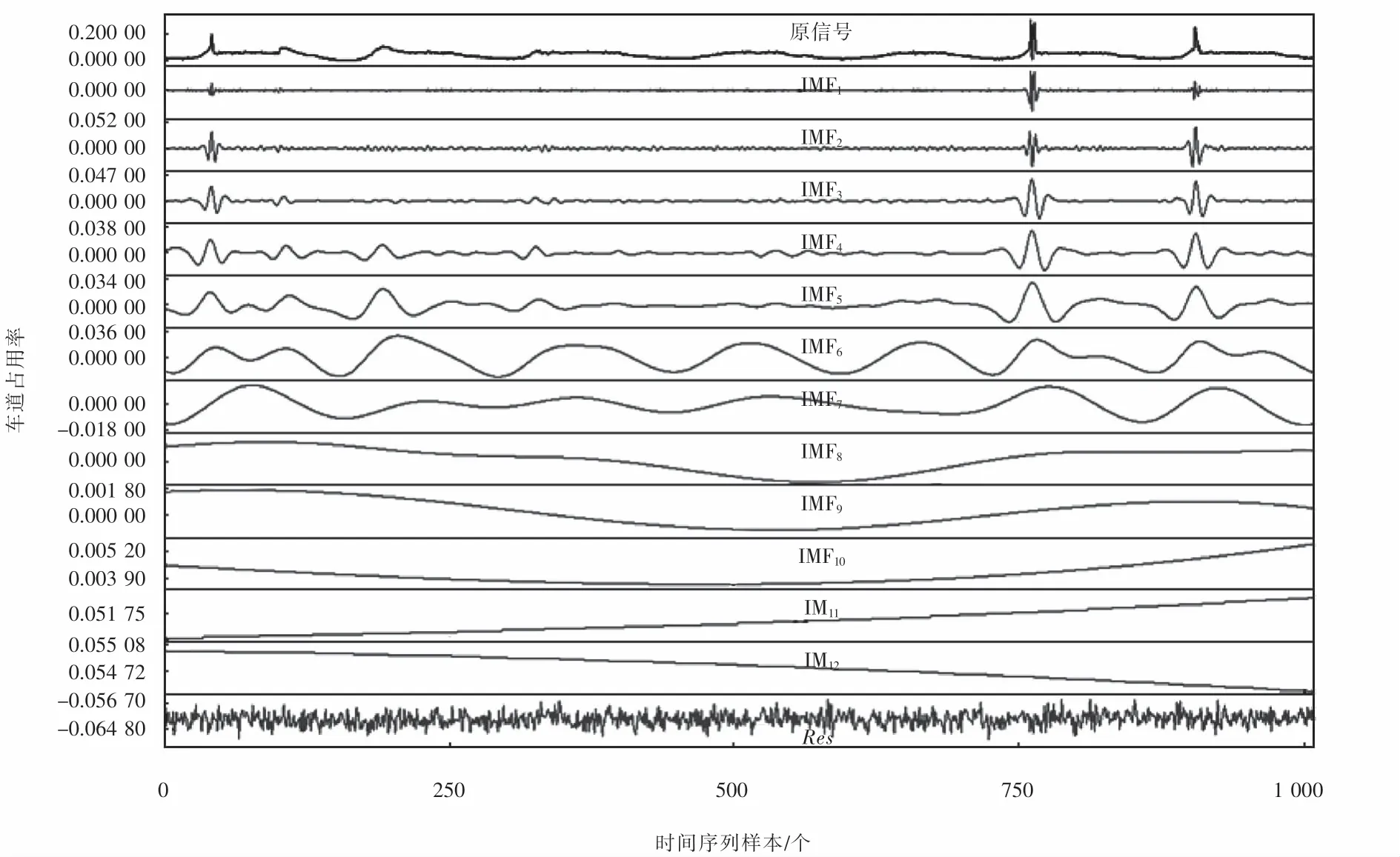
图4 EEMD分解结果Fig．4 Decomposition results of EEMD

原始信号经分解降噪和集合平均后得到的信号ai如下：

2 预测模型的建立

2.1 双向长短期记忆网络

由于道路路况不断复杂化，交通流数据量不断增加，传统的递归模型的精度难以满足数据预测分析的要求.近年来，越来越多的学者开始使用长短期记忆网络进行交通流预测，LSTM网络相比传统的循环神经网络加入了运算门的设计，克服了短时记忆的影响，并且缓解了权重消失和梯度爆炸的问题［17］.单个LSTM神经元的结构如图5所示，其输入门、遗忘门、输出门、长期记忆、短期记忆和候选状态的运算过程见式（5）～（10）.

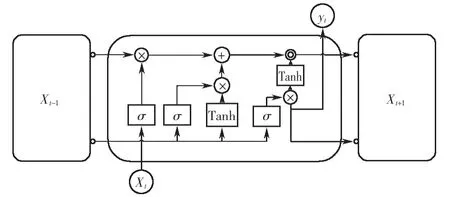
图5 单个LSTM单元的内部结构Fig．5 Internal structure of single LSTM unit

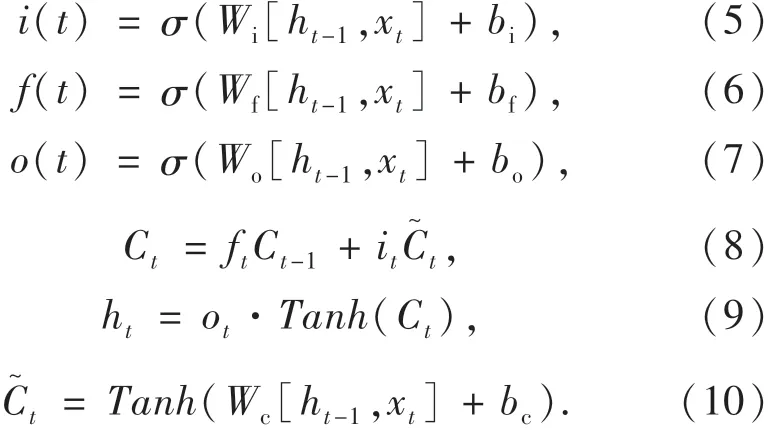
BiLSTM在LSTM的基础上对网络结构进行改 进，使用两个LSTM网络分别从正向和反向读取输入信号，然后将各自的输入、输出结果拼接起来作为BiLSTM的输出，其结构如图6所示.

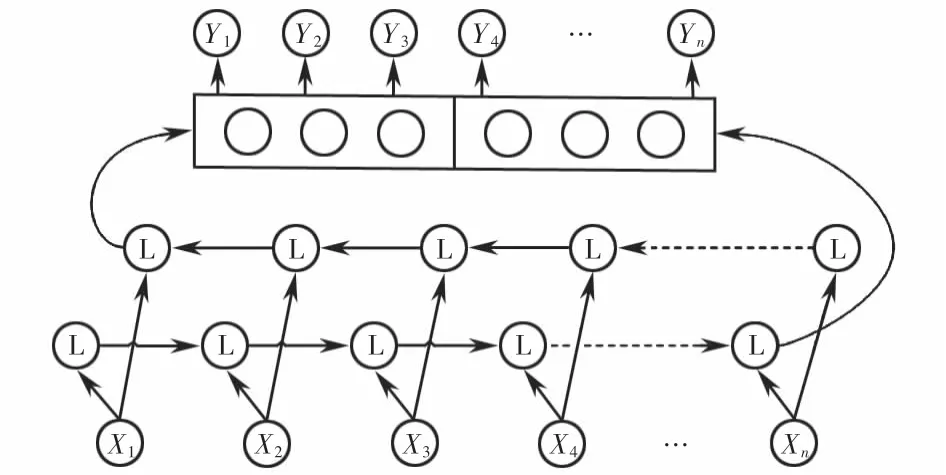
图6 BiLSTM网络结构Fig．6 Structure of BiLSTM

2.2 注意力机制

文献［18］提出了一种注意力机制，以提高递归神经网络模型的特征提取能力.AM为不同的特征分配不同的注意权重，以便数据驱动模型能够更加关注训练过程中的重要部分.

AM的结构图如图7所示，将输入值（X1，X2，…，Xn）输入Encoder网络进行运算后输出结果（a1，a2，…，an），而此时，每一个Encoder网络的输出值会在AM网络中乘一个权重因子α并进行叠加，叠加后的值作为Decoder网络的输入值进行训练，最终得到网络的输出值（Y1，Y2，…，Yn）．其中：ak表示Encoder网络中第k个单元经激活函数Tanh激活后的函数值；Sk表示Decoder网络中第k个单元经激活函数Tanh激活后的函数值；α（i，j）为第一层LSTM网络的第i个单元输出至Decoder网络第j个单元所对应的权重因子，满足表达式（11）～（12），且由式（13）确定.

图7 AM结构图Fig．7 Structure of AM

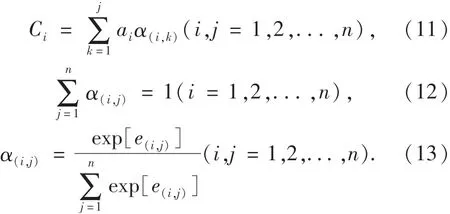
其中：e（i，j）值可以由训练一个简单的神经网络来确定，网络输入为Encoder网络的激活值aj和Decoder网络上一时刻的激活值Si-1，输出则为e（i，j）．

2．3 EEMD-BiLSTM-AM模型

本文所提出的EEMD-BiLSTM-AM模型结构如图8所示，将车道占用率信号经过数据预处理后作为输入信号，首先经EEMD将输入序列由多特征影响的高度非平稳序列分解为IMF1～IMF12和Res这些由单一特征影响的平稳子序列；每一个子序列的采样值按照Encoder-Decoder框架输入BiLSTM网络，来预测下一时刻的车道占用率；随后又将预测出的输出采样值和其上一时刻的采样值作为新的输入特征，继续来预测下一时刻的车道占用率；最终，预测出一个时间段内的车道占用率.本文中的BiLSTM网络中的正向和反向LSTM网络分别由400个LSTM单元构成，每200个单元后增设一个舍弃率为30%的随机舍弃层来提高运算效率；随后在输出端增加注意力机制，提升模型训练过程中关键神经元的影响权重；最后将各模态所建立的子模型进行叠加重构.

图8 EEMD-BiLSTM-AM结构Fig．8 Structure of EEMD-BiLSTM-AM

本次研究在训练过程中使用Adam算法用于网络训练的反向传播过程中的参数优化.Adam算法是一种常用的优化算法，相比传统的梯度下降算法，Adam算法结合了Momentum算法和RMSprop算法的优势，即计算梯度的指数加权平均数，用该梯度来更新权值w和偏置b，减小了优化过程中的纵向波动，增加了优化速度，提高了训练效率［19］.

本研究将已知的数据集划分为训练数据集和测试数据集，将训练数据集进行EEMD分解，对分解得到的每一个子模态进行训练建模，通过迭代预测的方式得到下一时间段的交通流分量信号，将各模型输出的分量信号叠加，所得到的预测值与测试数据集进行对比，对模型性能进行评估.

在实际预测中，对当前时间前的交通流信号进行分解，获得信号序列，然后采用相应模态下的模型，根据当前时间前的交流通信息，迭代预测出相应模态下的交通流信息，然后再进行叠加即可获得未来时刻的交通流预测值.

3 结果分析

为了充分验证EEMD-BiLSTM-AM的性能，本文设计了LSTM，BiLSTM，BiLSTM-AM，EMD-BiLSTM，EMD-BiLSTM-AM，EEMD-BiLSTM等神经网络模型，并将这些模型作为竞争模型，与EEMD-BiLSTM-AM进行对比研究.选取均方根误差（RMSE）、平均绝对误差（MAE）、平均绝对百分比误差（MAPE）和决定系数R2对模型进行评价，其表达式如（14）～（17）所示．

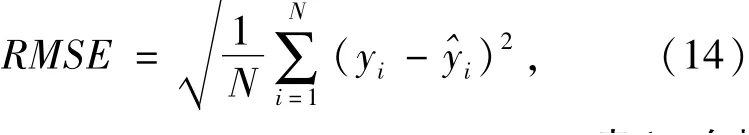
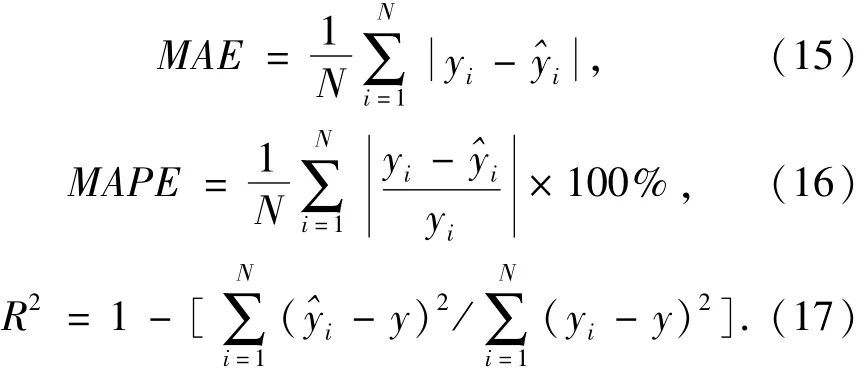
其中：N为数据量大小为预测值；yi为真实值.

为了更好地比较各个模型的性能，各竞争模型所用训练数据集与测试数据集和EEMD-BiLSTMAM模型一致，各竞争模型中，BiLSTM网络使用400个神经元，每200个单元后增设一个舍弃率为30%的随机舍弃层抑制过拟合，预测时间步长为5，训练时每批送入模型的样本数设置为64个，激活函数使用ReLU函数，损失函数选取MSE，优化算法为Adam，迭代次数为200次.

各模型经计算得到的评价结果见表1.由表1可知：BiLSTM模型的各项误差均低于LSTM模型，且其R2值为0.879 9，高于LSTM模型的0.878 1，说明BiLSTM模型性能优于LSTM模型.BiLSTM不仅可以将神经元中遗忘门保留的上一时刻更有用的信息传送到下一时刻的神经元中［20］，滤除冗杂信号，而且可以从正向和反向两个方向读取序列信息，更好地捕捉不同采样点间的依赖关系.

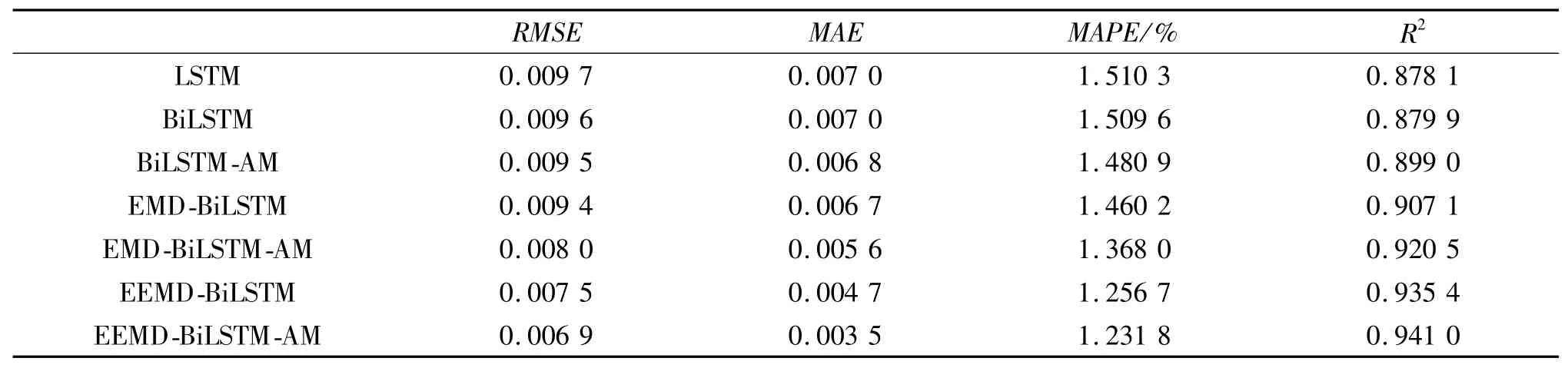
表1 各模型的评价结果Tab．1 Evaluation result of each model

使用模态分解后，模型的预测精度大幅提升，EEMD和EMD可以有效地将交通流中具有代表性的特征模态分离开，根据不同特征的信息建立相应的模型，更加有效地预测各特征信号；同时，使用EEMD的模型在进行训练时，抑制了训练数据中各模态的混叠现象，降低了训练误差，进而提升了模型的预测能力.各模型在加入AM层后，预测误差降低，预测精度提高，表明AM使模型捕捉到了序列中影响交通流趋势走向的关键时间点，使模型更加有针对性地进行预测，进而提高了模型的计算精度.

相比于竞争模型，本文所提出的EEMD-BiLSTMAM模型的RMSE，MAE和MAPE达到最低值0.006 9，0.003 5和1.231 8%，而R2为最高的0.941 0，其预测能力明显优于其他竞争模型.

以2008年3月19日和2008年3月20日为例，以热力图的形式表示在两日内AM层的权重分配，如图9（a）和图9（b）所示.由图9可知：对于3月19日，AM层把更高的权重分配在5∶00-8∶00和16∶00-18∶00的时间段，这两个时间段分别对应了该日交通流信号在早晚期间的上升和下降过程；对于3月20日，AM层把更高的权重分配在6∶30，8∶30，20∶00和22∶00时刻，这4个时刻分别对应了该日交通流信号在早晚期间上升、下降过程的起止时刻.这种注意力权重分配规律，有助于模型捕获对于信号变化影响力更强的关键时间段.

图9 3月19日和3月20日AM层权重分配Fig．9 AM layer weight distribution of March 19 and March 20

将各算法所预测的车道占用率预测值与真实值进行比较，对比结果如图10所示.各模型的训练时间如图11所示.由图10可知：LSTM，BiLSTM和BiLSTM-AM模型对于模型的跟踪能力较弱，而EEMD-BiLSTM和EMD-BiLSTM-AM模型虽然整体预测精度较高，但在局部区域的预测偏差比较明显；本文所提出的EEMD-BiLSTM-AM模型不仅可以精确稳定地跟踪真实值的变化趋势，并且在预测局部时间段信号的能力也明显优于其他竞争模型.

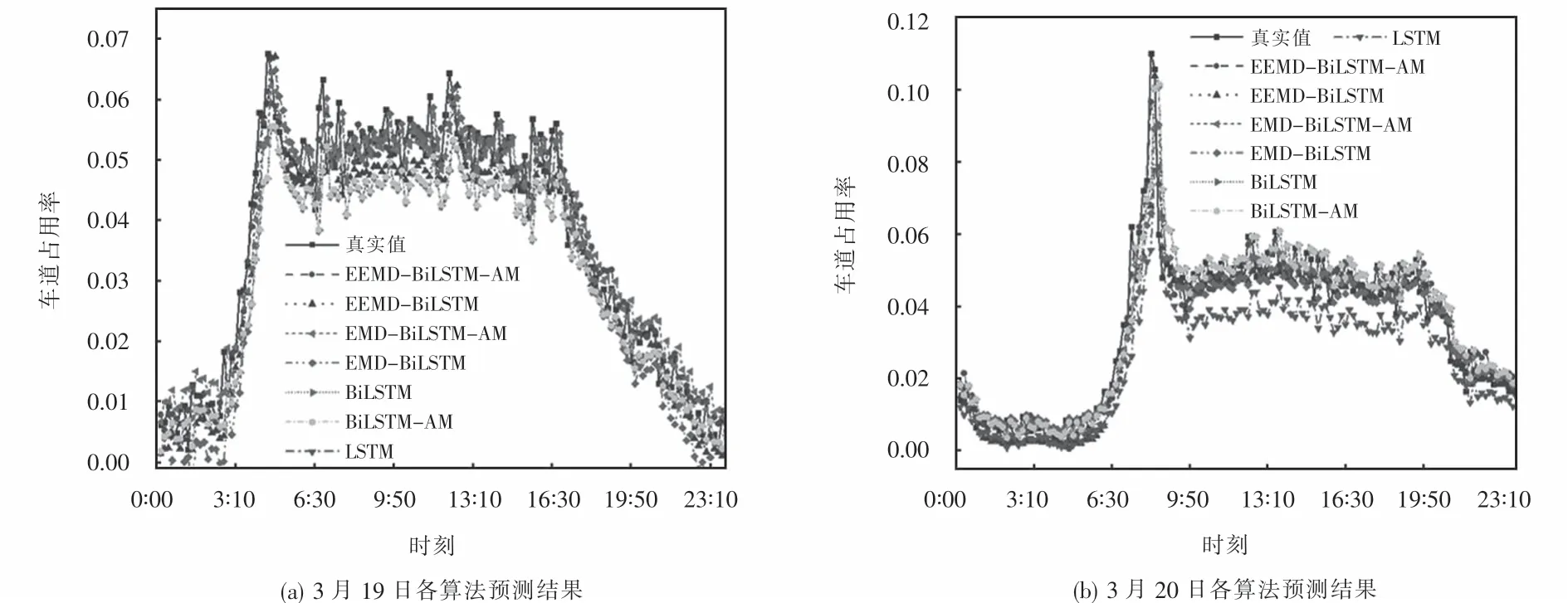
图10 3月19日和3月20日各算法预测结果对比Fig．10 Prediction results comparison of the algorithms on March 19th and March 20th

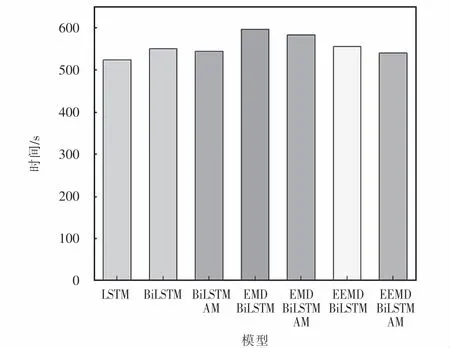
图11 各模型训练时间对比Fig．11 Comparison of training time of the models

本实验硬件配置为Corei7-6820CPU＠2.70 GHz，16 GByte内存.使用Python3.8进行编程，并使用Tensorflow2.1框架构建算法模型.在学习速度方面，LSTM，BiLSTM，BiLSTM-AM，EMD-BiLSTM-AM，EMD-BiLSTM，EEMD-BiLSTM，EEMD-BiLSTM-AM分别需要训练525，552，545，597，584，557，541 s，EEMDBiLSTM-AM虽然增加了模型复杂度，但训练时间并未大幅增加，且其预测精确度和稳定性都显著优于其他竞争模型.在预测时间方面，每一个子模态模型平均需要0.104 s的预测时间，总时间为1.248 s，基本可以满足实时性的需求.

4 结论

针对高速公路短期交通占有率预测问题，本文

提出了一种EEMD-BiLSTM-AM融合神经网络模型，EEMD解决了EMD方法中出现的模态混叠问题，将交通流输入序列由多特征影响的高度非平稳序列分解为由单一特征影响的平稳子序列；每一个子序列的采样值按照Encoder-Decoder框架输入BiLSTM网络，来预测下一时刻的车道占用率；同时，AM为不同的交通流特征分配不同的注意力权重，使得融合神经网络更加关注训练过程中的信息流的关键部分，充分挖掘交通流的时空特征.本文结合旧金山湾区高速公路某路段的车道占用率实测数据对模型进行验证.预测结果表明：所提出的融合神经网络模型预测精确性及稳定性显著优于LSTM，BiLSTM，BiLSTM-AM，EMD-BiLSTM，EMD-BiLSTM-AM，EEMDBiLSTM等6种竞争模型；相比于EMD，EEMD在抑制噪声对信号模态分解的负面影响中表现更优，且AM能够帮助神经网络模型重点关注交通流信号的关键时空信息，在不显著增加训练时间的前提下，提升了融合神经网络的预测性能.下一步的研究重点是考虑其他因素，如车辆行驶速度、车流量、天气、路段空间位置等对交通流预测的影响，进一步挖掘这些因素与交通流的时空相关性.