反比例函数易错点的“提前干预”

◎赵 玲 王 淳

(1.西华师范大学数学与信息学院，四川 南充 637000;2.成都市新都一中实验学校，四川 成都 610500)

一、反比例函数的概述

按照学习内容来分，反比例函数可以分为反比例函数的概念、反比例函数的性质、反比例函数的综合应用三个部分反比例函数是学生学习函数、正比例函数之后继续学习不同类型函数的深化同时，反比例函数的学习也为高中阶段学习双曲线打下坚实的基础，起到了承上启下的作用从近几年中考题考查的内容来看，反比例函数与其他知识点相结合的考查次数越来越多，是中考题的重要考点之一因此，从这三个方面可以看出在初中阶段学习反比例函数的重要性

二、在教学反比例函数时存在的问题

在反比例函数的教学过程中，普遍存在一种现象：课堂教学时学生一听就懂，但知识点一讲完就忘，课后题一做就错，然后教师在相关的习题课中进行“补救”，这种教学方式易导致学生难学，教师难教，效果不好这是因为学生听懂老师所讲知识和自己真正学会知识是两个不同层次的认知结果学生“听懂了”可能是由于课上机械记忆和简单模仿正确回答导致，实际上其对知识的认知只停留在机械记忆和表层理解这一层次再反思习题课的“补救”过程，教师只是简单地讲评错题，一味地重复训练，以弥补新授课中的不足，但这并不能从根本上解决问题学生已对易错点先入为主，在记忆环节已经留下“痕迹”，故教师很难在其认知结构中进行纠正如果教师在课前对收集的易错题进行分类整理，找出其中的易错点，从学生没有纳入认知结构的易错点进行分析，找出错误的原因，可为预判新授课中的易错点做准备在新授课中，教师将这些易错点与学生认知结构中已有的观念建立实质性的联系，从而进行有意义的学习，就是对反比例函数易错点的“提前干预”

三、易错点剖析

收集大量反比例函数的易错题是教师新授课时预判易错点的重要依据教师通过对反比例函数易错题进行分类整理，找出其中易错的知识点，对易错点进行分析，找出错误的原因，可为新授课中反比例函数易错点的“提前干预”做准备

(一)反比例函数概念

1将反比例关系和反比例函数混淆

1下列函数中，是反比例函数的是( )

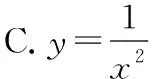
对解析式的形式记忆混淆，认为后两项也是反比例函数，主要原因是不能区分反比例关系和反比例函数的差异反比例关系中的，既可以代表单项式也可以代表多项式，而反比例函数中的两个变量只能分别由一个字母表示因此，满足反比例关系的两个变量不一定是反比例函数，但两个变量满足反比例函数的表达式一定成反比例关系所以C，D两项是反比例关系，但不是反比例函数

2忽略≠0

2若函数=(-1)-2是反比例函数，则的值是________

学生易由-2=-1，得出=±1,主要原因是忽略≠1这一条件，没有真正理解反比例函数中≠0的含义如果反比例函数中的=0，无论取何值都有=0，这时不随的变化而变化，故不满足反比例函数的定义

(二)函数图像和性质

1不分象限讨论函数增减性

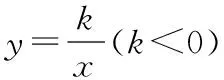
学生易根据<0判断函数随的增大而增大，从而得出<<，主要原因是没有理解反比例函数图像不过原点以及必须分象限讨论增减性这里可以从两个角度理解图像不过原点的含义，在数方面的体现是分母不能为0，在形方面的体现是图像不过原点，因此，其图像必定分成两支由于在图像的两支上各取一点(-1,)和(2，)，虽然-1<2，但是>，不满足随的增大而增大的性质，因此，对于反比例函数必须分象限讨论增减性

2将反比例函数的值与一次函数值混淆

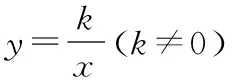
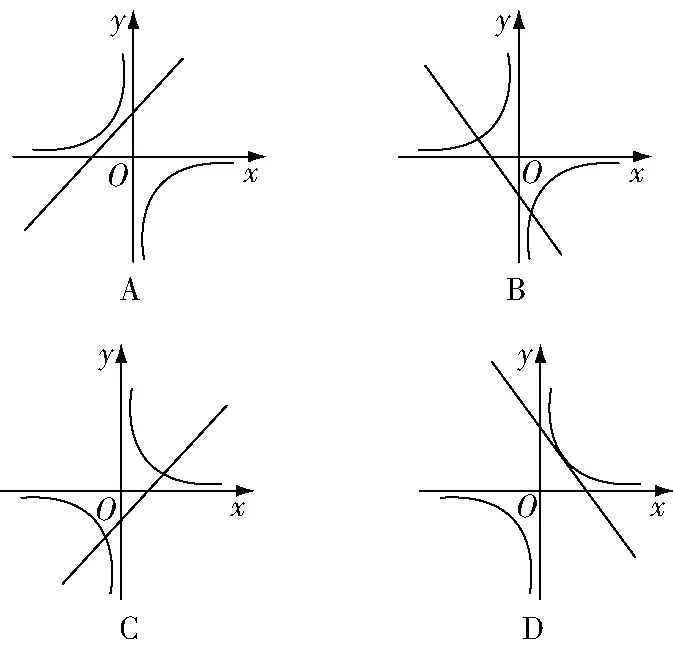
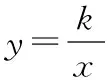
(三)k值的几何意义

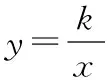
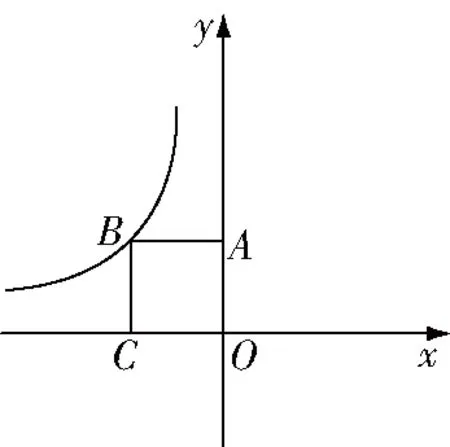
图1

学生易根据正方形的面积为4和=，得出=4，出错的主要原因是忽略了结合图像所在象限确定的符号，没有建立的几何意义在逻辑基础上的联系，没有真正体会知识的形成过程

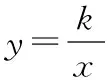
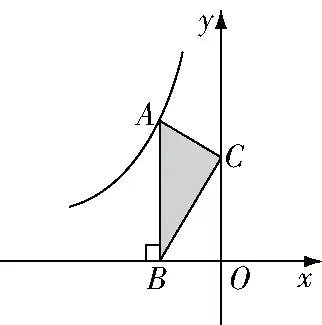
图2

A.4 B.-4 C.8 D.-8

四、易错点的“提前干预”

对反比例函数的易错点进行剖析，可发现主要是学生对这些知识存在表层理解和机械记忆，在做题时记忆提取环节出现障碍为了从根本上减少学生在学习反比例函数时出现的这些问题，教师就要在新授课中对这些易错点进行“提前干预”，也就是在反比例函数的新授课中将这些易错点作为教学关键点，与学生认知结构中已有的观念建立实质性的联系，从而进行有意义的学习

(一)以原有经验为基础，促进概念同化

1下位联系函数概念

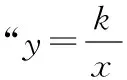
2并列联系分式成立条件

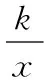
(二)设计比较性组织者，促进学生对性质的理解

1设计比较性组织者，突破性质教学的关键点

教师可用“描点法”，并借助几何画板动态展示几组函数图像，借助一次函数性质的知识结构推想反比例函数的性质，引导学生分>0和<0的情况进行讨论首先讨论>0的情况，教师教授学生运用动态的眼光分析函数图像，直观地看出在第一象限内随的增大而减小，在第三象限内也随的增大而减小

教师提问学生：“能否说当>0时，反比例函数随的增大而减小呢？请同学们思考，并说出自己的理由”这是教学的关键点教师通过学生的回答可充分了解学生的思维过程，同时找到学生认知结构中“观念的支架”，以此引导学生进行有意义的学习

为了突破教学关键点，教师可以设计比较性组织者，例如，一次函数=+(<0)能说成随的增大而减小，是因为我们在其图像上任意取一点都满足这个性质，这里的具有任意性教师提问：“如果我们在反比例函数图像的两支上各取一点，是否也具备这种任意性呢？”通过与一次函数进行比较，学生自然就明白了为什么反比例函数要分象限讨论增减性然后利用类比思维，学生可自行分析反比例函数中<0的情况

2设计比较性组织者，提高不同函数增减性的可辨性

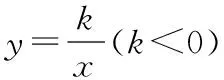
(三)找到逻辑基础上的联系，建立k的几何意义

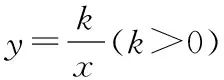
教师提问学生：“如果在第二象限、第三象限或第四象限中任意取一点，也就是说横、纵坐标值有负数怎么办？”这是教学的关键点

由于绝对值可将负数变为正数，这是学生原有的认知结构，因此，学生会想到将横、纵坐标值加绝对值，这样无论横、纵坐标是正数还是负数，加了绝对值后都能将其转化为正数，从而找到||等于横、纵坐标所作垂线与两个坐标轴所围成的矩形面积在逻辑基础上的联系教师通过层层引导，遵循知识的内在结构和学生的认知规律、心理意愿，让与之相关的知识从学生的认知结构中自然生长出来

五、结束语

目前，易错点的干预方案大部分是教师在习题课中进行“补救”，这种干预方式不仅难以纠正学生的错误认知，还会加重学生的课业负担本文提出将课前收集的易错题分析、整理成易错点，作为教师预判新授课中易错点的依据，并在新授课中将这些易错点作为教学关键点进行有意义学习的教学策略这种策略从概念的同化、设计比较性组织者及找到逻辑上的联系这三个角度，分别在学生的学习过程中将反比例函数的概念、性质以及的几何意义这些新知识与学生认知结构中已有的观念建立逻辑基础上的联系，指导学生进行有意义的学习，避免学生对新知识停留在机械记忆和表层理解上，从而在根本上减少学生在易错点上出错的概率这种“提前干预”的教学策略不仅能够引导学生在新授课中对反比例函数的相关知识建立正确的认知结构，有利于学习的迁移，也能防止学生在学习新知识的过程中产生思维惰性，对习题课中的“补救”产生依赖思想，有利于良好学习习惯的养成