新型双腔油气式磁流变减震器阻尼特性分析与仿真

祝世兴，李佩窈，魏 戬

(1.中国民航大学 航空工程学院，天津 300300；2.昆明理工大学 机械学院，云南 昆明 650000)

引言

飞机起落架是飞机起降过程的主要承力部件，通常在大范围激励条件下工作，但目前飞机普遍采用油气式减震器或全油液式减震器，无法根据外部激励的变化而实时的调节系统的刚度与阻尼，受环境影响较大[1]。为改善系统的动态特性，可利用磁流变智能材料作为减震器的减震介质[2]，减震器可以根据受载情况的变化调节系统的外加电流进而控制系统阻尼。

磁流变液最早是由美国国家标准局的Jacob Rainbow于1949年发现[3-4]，其对磁场强度变化的快速响应、可逆以及在高屈服应力下易于控制等优点，广泛应用于各种振动控制系统中[5-6]。

ZHENG Jiajia等[7]设计了一种新型可变电阻间隙多线圈磁流变减震器并对此结构进行优化，并在正弦和三角形位移激励下的振动性能与典型的多线圈磁流变阻尼器的振动性能进行比较。JIANG Rilang等[8]针对直升机旋翼提出了一种新型磁流变液-弹性减震器，在不同输入电流与幅变频变的动态激励下对提出的减震器进行实验，提出了一个新的唯象模型来描述所提出的减震器的非线性动力学特性并进行实验验证。HAN C等[9]结合被动式油气减震器设计了一种采用机械式被动反冲阀的磁流变减震器，使其在正反行程下产生不同的阻尼力。BATTERBEE D C等[10-12]基于油气减震器的结构尺寸设计了一种新型磁流变减震器，并考虑到流体可压缩性对降低减震器的可控性的影响，建立该减震器的等效动态模型，应用数值方法对该模型进行冲击模拟并进行实验验证。

为提升减震器的减震效率、降低着陆动载荷、增加减震器的阻尼调节功能。本研究基于磁流变原理，依据双腔油气式减震器的基本结构形式，设计了孔缝结合的可变阻尼通道的油气式磁流变减震器，将传统被动油气式减震器改进为半主动油气式磁流变减震器，并对孔缝结合形式的阻尼通道进行了磁路优化，利用Maxwell软件模拟减震器电磁回路产生的磁场，分析阻尼通道内磁感应强度的分布。利用有限元方法对其进行阻尼力的仿真计算，将不同阻尼通道形式下的初始输出阻尼力与动态可控阻尼力的输出结果进行对比分析与验证。

1 磁流变减震器的阻尼结构设计

由于常规双腔油气式减震器的结构形式和参数并不能满足双腔油气式磁流变减震器的结构和使用要求，必须根据双腔油气式磁流变减震器结构特点和使用要求进行减震器的结构改进设计，特别是阻尼通道形式和尺寸设计，以提升初始阻尼力和可控阻尼力的变化范围。针对上述要求，依据双腔油气式减震器的工作原理和一般结构形式，完成了阻尼通道处的结构设计，并对磁路进行了优化，具体形式如图1所示。双腔油气式磁流变减震器由缸筒、浮动活塞、内筒、端盖以及励磁线圈等部分组成，以某型无人机为例，其基本参数如表1所示，并以此数据进行计算和分析。

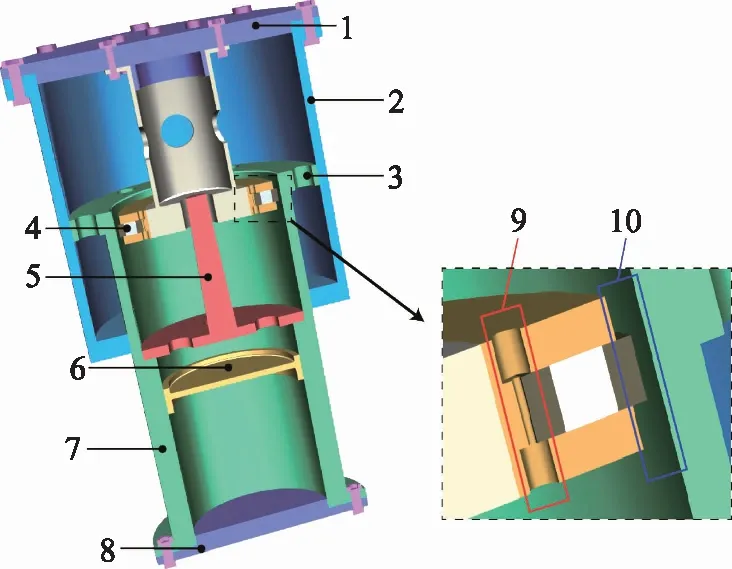
1.上端盖 2.缸筒 3.回油孔 4.线圈 5.油针 6.浮动活塞 7.内筒 8.下端盖 9.圆孔阻尼通道 10.缝隙阻尼通道

表1 某型无人机基本参数

选取压缩比为p1∶p2=1∶2.1，p3∶p2=1.9∶1，其中p1为全伸长时的气体压力，p2为停机时的气体压力，p3为全压缩时的气体压力。减震器低、高压腔初始参数由表2所示。

表2 双腔油气式磁流变减震器低、高压腔初始参数

忽略摩擦力的影响，以正弦信号为激励，分析减震器加载的动态过程，则双腔油气式磁流变减震器内部阻尼力Fs为：

Fs=Fa+Fη+Fτ

(1)

式中，Fa——空气弹簧力

Fη——磁流变液黏滞阻尼力

Fτ——磁流变液库伦阻尼力

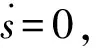
(2)

式中，Ad(t)——活塞面积函数

D(t)——油针直径变化函数

z——修正系数

最终计算出油针的直径D随时间变化的曲线，如图2所示，进而确定油针的角度大小。

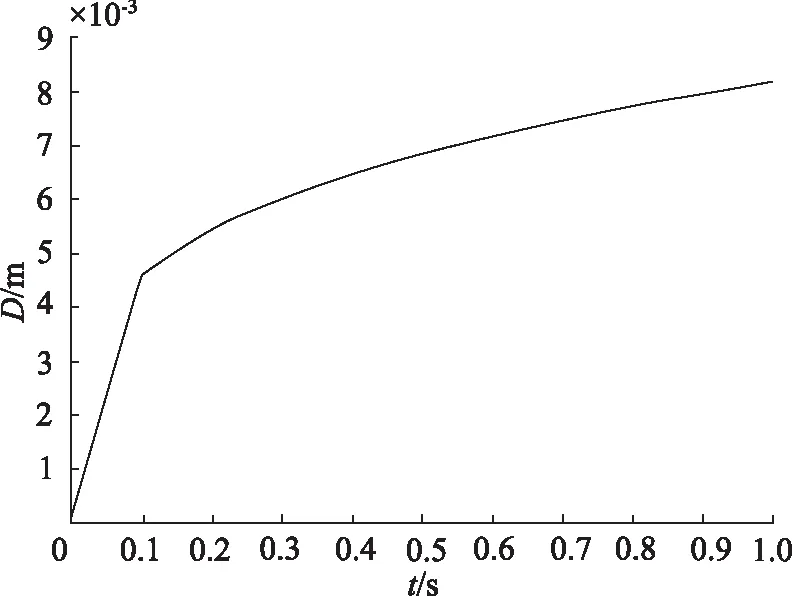
图2 油针直径随时间变化曲线

由图2可知，选取油针顶部直径为5 mm，底部直径为8 mm，确定油针角度为89°。

2 双腔油气式磁流变减震器磁路设计

双腔油气式磁流变减震器的磁路是由导磁环、隔磁环、励磁线圈等部分组成，图3为磁路的结构示意图。

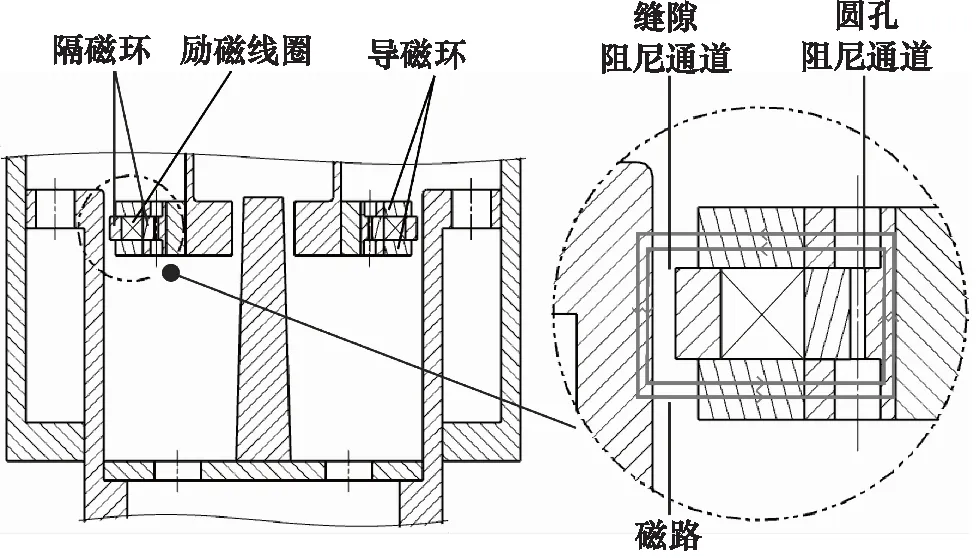
图3 磁路结构设计图

在结构尺寸一定的情况下，为提升半主动双腔油气式磁流变减震器的可控区域，通常采用的方法为延长阻尼通道长度、改变阻尼通道间隙或通过合理设计磁路结构来提升减震器的可控区域。

然而阻尼通道过于延长或狭窄会导致磁流变液在工作过程中流动性变差，阻尼力的可控范围减小，适用性降低。因此，合理的阻尼通道和磁路设计是提升磁流变减震器性能的关键。

假定阻尼力为10000 N，有效阻尼通道长度为L=0.014 m，对于导磁材料，其相对磁导率在未达到饱和状态的时处于较高的状态，达到饱和后迅速下降，这种情况会导致整体磁路的瓶颈，磁流变减震器的减震效率降低，减震效果变差，因此如何避免上述情况的发生是保证磁通均衡的关键问题。对于磁路截面尺寸的优化问题，基于磁通均衡原理对截面进行合理的计算。

忽略漏磁因素的影响，根据双腔油气式磁流变减震器的磁路简图，结合励磁线圈产生的磁力线闭合回路，由图4所示，得到磁路中各部分的磁通量。

1、2.导磁环 1_1、1_2、2_1、2_2.侧导磁环 3、4.缝隙阻尼通道 5、6.圆孔阻尼通道 7.内筒 8.内导磁通路

导磁环磁通量为：

Φ1=Φ2=B1πd3L1

(3)

式中，B1——导磁材料饱和磁感应强度

侧导磁环磁通量为：

(4)

阻尼通道间隙处磁通量为：

(5)

式中，B2——磁流变液饱和磁感应强度

内筒与内导磁通路处的磁通量为：

Φ7=Φ8=B1πd3L1

(6)

由磁通均衡原理：

Φ1=Φ1_1=Φ1_2=Φ2=Φ2_1=Φ2_2=Φ3…=Φ8

(7)

边界条件：

(8)

根据式(3)～式(7)，以式(8)为边界条件计算最优结果。首先应用遗传算法缩小多目标优化解变量范围，而后应用Newton迭代法求解最优的设计变量，使得模型的磁通量最大，同时磁路中各部分的磁通之差达最小，该多目标优化参数问题可以表示如下形式：

Find:X=[d1d2d3L1L2L3]

Maximum:AkX=Φk

Minimum:e(X)=∑[Φ(Xi)-Φ(Xi-1)]2

Subject to:d1∈[2，8]，d2∈[1，3]，d3∈[1，3]，

L1∈[0.5，4]，L2∈[2，8]，L3∈[1，6]

式中，X——磁路截面优化参数向量

Φk——磁路中各部分磁通量，k=1，2，1_1，1_2，2_1，2_2，3，…,8

e(X)——误差函数，定义磁路中各部分的磁通之差

最终参数优化结果如表3所示。

表3 磁路截面优化参数

由于双腔油气式磁流变减震器的结构为对称结构，因此取部分磁路进行研究分析，本研究均以左半部分为例。在Maxwell中对双腔油气式磁流变减震器进行了磁路仿真，仿真结果如图5所示。

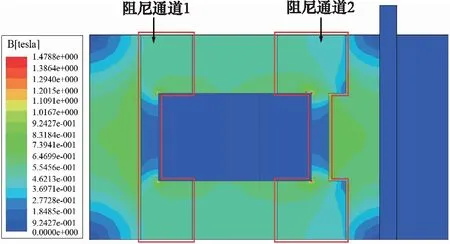
图5 电流为1 A时部分磁路磁感应强度仿真结果

图5为励磁线圈的电流1A时所对应的结果，从磁感应强度B的分布可以看出，缸筒的饱和磁感应强度在0.9～1.3 T之间，磁流变阻尼通道的饱和磁感应强度在0.6～1.0 T之间，这表明阻尼通道处达到磁饱和时金属材料得到充分的利用，且磁感应强度分布比较均匀，磁路结构参数设计合理。图6、图7为不同外加电流下缝隙阻尼通道1与圆孔阻尼通道2的磁感应强度延垂向方向的分布。结果表明，阻尼通道内的主要工作区域分布在阻磁环两端，中间部分磁感应强度较低且变化较为平稳。

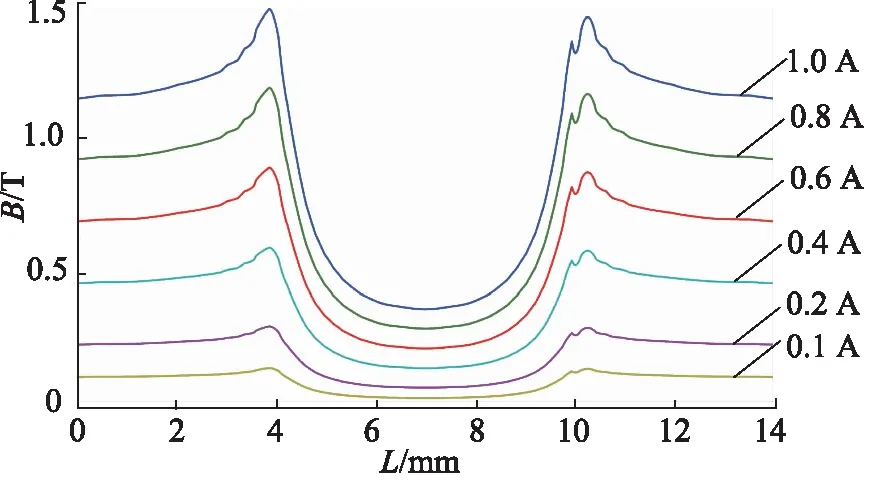
图6 缝隙通道的磁感应强度轴向分布

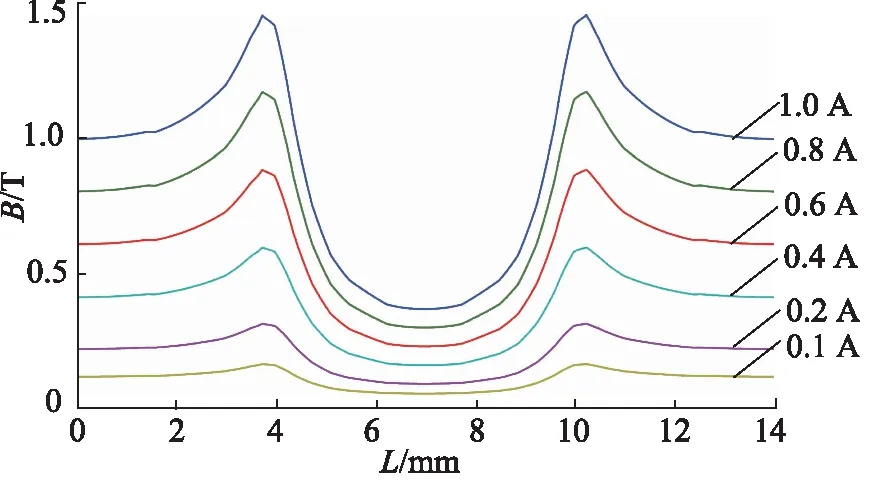
图7 圆孔通道的磁感应强度轴向分布

3 孔缝结合阻尼通道的对比分析

与仅有缝隙阻尼通道或仅有圆孔阻尼通道磁流变减震器相比，采用孔缝结合的方式不仅避免磁路的浪费，并且增加双腔油气式磁流变减震器阻尼力的初始输出与可控范围。

为更好的分析孔缝结合情况下的可控范围，现对以下4种情况进行比对：

Case1.仅有油针；

Case2.缝隙阻尼通道与油针；

Case3.圆孔阻尼通道与油针；

Case4.孔缝结合阻尼通道与油针。

给予该减震器落震冲击激励来模拟飞机的落震过程，具体参数由表4所示。

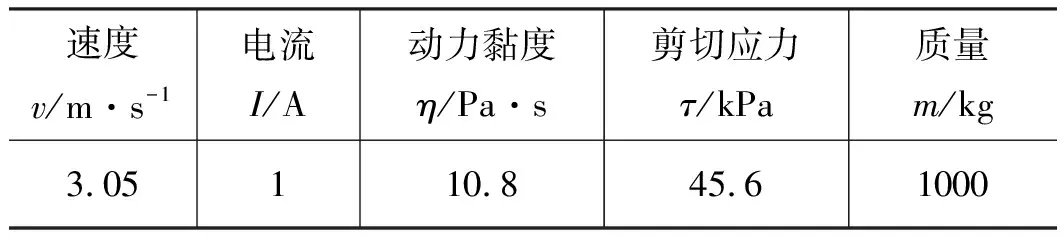
表4 双腔油气式磁流变减震基本参数输入

在落震冲击的工况下，图8显示了4种情况的在零磁场和磁饱和情况下的输出阻尼力F对比。孔缝结合阻尼通道所产生的阻尼力明显高于另3种情况，在零磁场条件下，圆孔阻尼通道初始阻尼力略大于缝隙阻尼通道，其原因是由于阻尼通道的尺寸略有差异，导致其前后压差稍大。而在磁饱和条件下，由于缝隙阻尼通道的调节阻尼力范围更宽，进而导致了缝隙阻尼通道的初始阻尼力大于圆孔阻尼通道初始阻尼力。

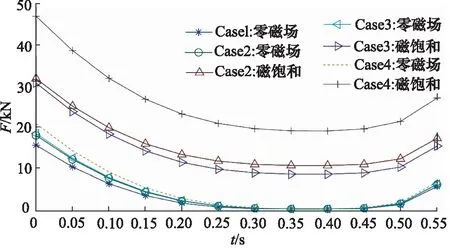
图8 不同情况下零磁场与磁饱和的阻尼力对比

表5显示了4种情况下初始阻尼力与可控阻尼力的大小。对比前3种情况，孔缝结合阻尼通道的初始阻尼力平均增加了15.4 kN，可控阻尼力平均增加了11.65 kN，可控动态阻尼比平均增大了10.15%。

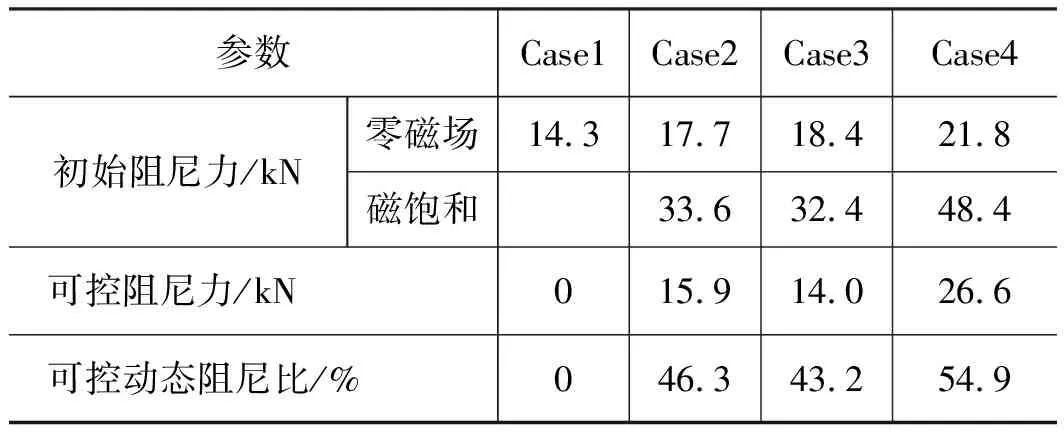
表5 不同情况下的阻尼力与阻尼比对比

4 结论

(1)优化后的磁路更为均匀，且有效的避免了磁路的浪费，在输入电流为1A时阻尼通道处平均磁感应强度最高达到0.94 T，最低为0.02 T，保证在磁饱和情况下磁流变液可顺利流过阻尼通道；

(2)圆孔阻尼通道提升了双腔油气式磁流变减震器的初始阻尼力，而缝隙阻尼通道增大了双腔油气式磁流变减震器的可控阻尼力的范围；

(3)采用孔缝结合方式所设计的磁路可控阻尼力平均增加11.65 kN，可控阻尼力平均提升10.5%。可控范围显著提高，整体性能优于缝隙阻尼通道与圆孔阻尼通道的形式。