轴向柱塞泵壳体降噪区域识别

叶绍干，李 旭，施嘉佳，侯 亮，卜祥建

(厦门大学 机电工程系，福建 厦门 361002)

引言

轴向柱塞泵结构紧凑、功重比大、工作压力等级高、变量方式多，在高端液压装备得到了广泛应用[1-4]。但作为液压系统的“心脏”，轴向柱塞泵振动大、噪声高，工作时产生的振动和噪声加剧零部件磨损、降低使用寿命[5-6]。

结构优化设计是改善轴向柱塞泵振动噪声特性的有效途径。学者对配流盘[7-10]、壳体结构[11-12]等进行优化设计，取得了良好的降噪效果。但是这种优化设计依赖工程经验，针对性较差，推广应用难度较大。

为了更有针对性的开展轴向柱塞泵的降噪优化设计，需要对其振动和噪声特性进行预测。CHRISTIAN S等[13]建立了轴向柱塞马达的声学有限元模型，通过实验验证了模型的准确度，但求解时仅考虑了柱塞马达壳体上的振声特性。PAN Yang等[14]对柱塞泵噪声传递路径进行了分析，但建模时未充分考虑内部零件之间的耦合关系。叶绍干等[15]建立了轴向柱塞泵辐射噪声仿真模型，并开展了实验验证，但并未对振声特性进行深入分析。权凌霄等[16]搭建了柱塞泵机械振动传递路径分析模型，分析了轴向柱塞泵振动机理及传递规律。叶绍干等[17-18]建立了轴向柱塞泵多质体多自由度动力学模型，分析了激励对振动的贡献，识别了关键激励。黄惠等[19]建立了柱塞泵马达的动力学模型，识别了关键的噪声激振源。上述研究为通过配流盘优化改善激振源的降噪方法奠定了基础，但是无法分析作为轴向柱塞泵最终辐射表面的壳体对噪声的贡献量，无法识别壳体关键辐射部位，难以指导壳体的优化设计。

本研究针对轴向柱塞泵壳体降噪区域识别难题，建立液压-多体动力学耦合模型以求解结构噪声激振力，建立考虑轴向柱塞泵内部多组件耦合关系的有限元/边界元振声模型，基于振声模型开展模态和板面声学贡献量分析，精确识别柱塞泵壳体降噪区域，为柱塞泵壳体优化设计奠定技术基础。

1 分析流程

本研究的分析流程包含两大部分：振声模型的搭建及柱塞泵壳体降噪区域的识别，具体流程如图1所示。

(1)轴向柱塞泵振声模型 为分析柱塞泵的振动噪声特性，建立了一种包含液压-多体动力学耦合模型、有限元模型和边界元模型的系统性振声模型。首先，建立通过液压-多体动力学耦合模型求解激振力；然后，对内部组件连接关系进行合理简化，建立轴向柱塞泵结构有限元模型，求解其振动响应；其次，通过锤击法模态试验及振动实验验证有限元模型的准确性；最后，将轴向柱塞泵的振动传递至声学边界元模型，计算其辐射噪声。

(2)轴向柱塞泵壳体降噪区域识别方法 基于轴向柱塞泵振声模型得到的辐射噪声分析结果，确定降噪优化目标。基于声学传递向量及模态声学贡献量的分析结果，确定板面划分区域，然后开展辐射噪声板面贡献量分析，确定对关键频率下辐射噪声贡献量突出的板面，识别柱塞泵壳体降噪优化区域。

2 液压-多体动力学耦合模型

2.1 结构噪声激振力

图2为斜盘式轴向柱塞泵的结构图，当其工作时，主轴在电机的驱动下带动缸体旋转，在与XY平面成一定倾角的斜盘作用下，柱塞在缸体孔内绕Z轴旋转的同时沿Z轴往复运动，引起柱塞腔内容积变化，完成轴向柱塞泵吸、排油过程。

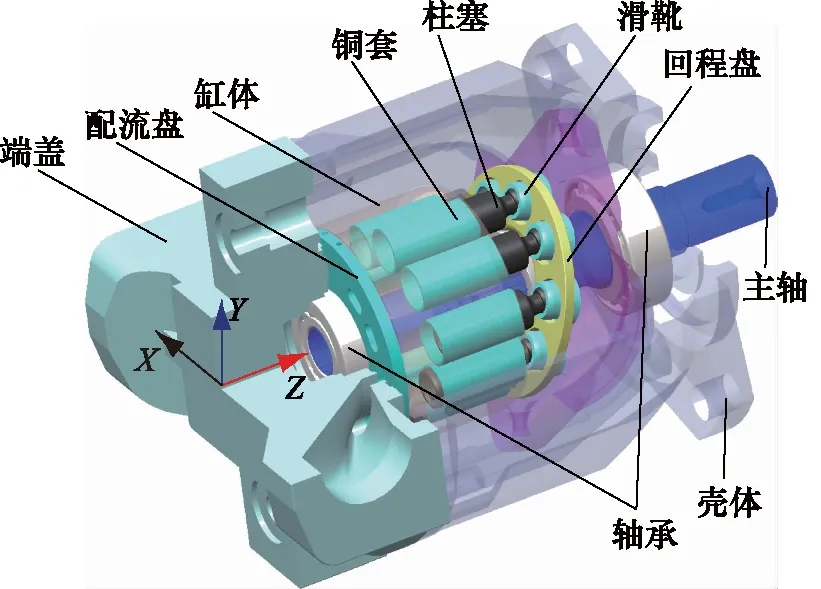
图2 轴向柱塞泵结构图

轴向柱塞泵运转过程中，周期性高低压切换的柱塞腔压力通过柱塞副、滑靴副、配流副、轴承油膜等分别传递到缸体、斜盘、配流盘、轴承，这些零件受到的力和力矩最终又传递到壳体和端盖，引起壳体和端盖的振动，产生噪声。将回程盘、滑靴、柱塞简化为一组件，则作用在配流盘和回程盘组件的激振力是导致轴向柱塞泵产生振动和噪声的主要原因[13]。在全局坐标系中，作用在配流盘的力和力矩为[13]：

(1)

在全局坐标系中，作用在回程盘组件上的力和力矩为[11]：

(2)

式中，FZ1，FZ2——作用在配流盘、回程盘组件上的轴向力

MX1，MX2，MY1，MY2——作用在配流盘、回程盘组件X，Y方向上的力矩

d——柱塞直径

pi——第i个柱塞腔压力

R——分布圆半径

θi——第i个柱塞的旋转角度

上述表达式表明激振力与柱塞腔压力直接相关。因此，获取柱塞腔压力是求得轴向柱塞泵激振力的前提。

2.2 激振力求解模型

轴向柱塞泵是高度液固耦合的元件，求解柱塞腔压力需要同时对流体和结构进行分析。因此，本研究搭建了由液压模型和多体动力学模型构成的轴向柱塞泵耦合模型，如图3所示。

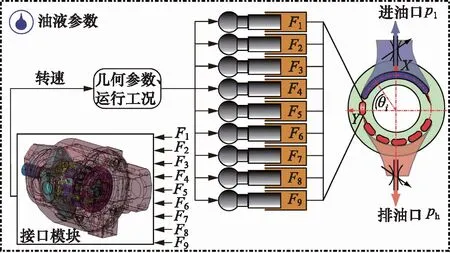
图3 液压-多体动力学耦合仿真模型示意图

首先，基于轴向柱塞泵的运行工况、结构参数、油液介质等构建了液压模型，主要参数如表1所示。在液压模型中，柱塞腔视为一个控制容积，通过计算进入和离开控制容积的流体来确定柱塞腔内的压力，柱塞腔瞬时压力变化为[1]：

表1 柱塞泵主要参数

(3)

式中，p——柱塞腔的压力

B——油液体积模量

Vpc——柱塞腔内流体体积

Qlp——进油口流量

Qop——出油口流量

Ql——泄漏流量

然后，根据柱塞泵的运动规律，搭建了多体动力学模型。在多体动力学模型中，通过赋予零部件材料属性、运动副设置等确定各零部件间的运动关系及力学传递。将9个柱塞底部设置的控制点作为液压模型所求得的输入量即液压力的施加点，同时将多体动力学模型中主轴的转速作为输出量导入到液压模型中。模型采用comsim联合仿真方式，通过两个模型间的接口模块来实现两个模型之间的实时数据交换。仿真工况：转速1500 r/min，出口压力14 MPa，时间步长0.0001 s，仿真时间0.04 s。

为了求解柱塞泵的振动和噪声，需要利用快速傅立叶变换(FFT)将时域激振力转换到频域。由于柱塞的数量为9个，仿真转速为1500 r/min，因此基频为225 Hz。在此基础上，将包括频率、振幅和相位信息的激振力导入到有限元模型作为载荷函数。

3 振声模型

3.1 零部件模态分析及验证

对轴向柱塞泵零部件进行网格划分及模态求解，获取5000 Hz内的模态信息。根据材料的不同，将零部件分为3类：壳体和端盖材料均为铸铁；滑靴材料为青铜合金；其他零件为碳钢。所有零部件均采用尺寸为4 mm的四面体单元进行网格划分，网格质量均满足要求。各零部件网格数量、节点数量如表2所示。结构有限元模型节点总数约为30万个，网格总数约为12万个[15]。

表2 主要零部件有限元模型信息

此外，对固有频率在5000 Hz内的壳体、端盖、斜盘、配流盘、回程盘等几个主要零部件分别进行锤击法模态试验，以验证其有限元模型的准确性。如图4所示，使用弹性绳将试验部件自由悬挂于台架上，试验采取移动力锤的方式，使用LMS数据采集仪同时对激励点与响应点的信号进行采集和处理，再求解试验模态。

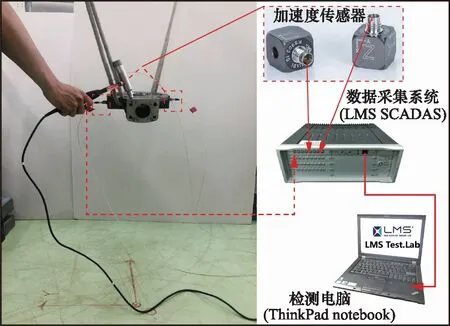
图4 零部件模态试验原理图

轴向柱塞泵主要零部件模态频率试验与仿真结果对比如表3所示，壳体前5阶模态频率试验与仿真结果相对误差在第1阶时最大，为3.9%；端盖前2阶模态频率试验与仿真结果相对误差在第2阶时最大，为2.2%；斜盘第1阶模态频率试验与仿真结果的相对误差达到3.1%；配流盘前3阶模态频率试验与仿真结果相对误差在第3阶时最大，为4.0%；回程盘前2阶模态频率试验与仿真结果相对误差在第1阶时最大，为1.5%。综上表明，柱塞泵零部件试验模态频率与对应的有限元模型仿真模态频率结果的相对误差均小于5%，在误差允许范围内[15]。

表3 试验与仿真的主要零部件模态频率对比

3.2 装配体有限元模型及模态分析

建立各零件的有限元模型后，需将各个零部件装配起来，以建立装配体的结构有限元模型。在装配体模型中，通过定义不同种类的弹簧或弹簧-阻尼单元，以模拟不同部件之间的连接。在定义弹簧或弹簧-阻尼单元之前，采用多点约束来定义不同零件的连接节点。零件连接节点被定义为主节点，周围的节点被定义为从节点，通过REB3单元创建各零件主从节点的关系。分别使用弹簧单元CELAS1或弹簧-阻尼单元CBUSH连接不同构件的主节点，并分别通过PELAS和PBUSH设定不同的刚度或刚度、阻尼系数以定义弹簧单元CELAS1和弹簧-阻尼单元CBUSH的特性，装配体结构有限元模型如图5所示[15]。

图5 装配体结构有限元模型

在装配体振动响应求解过程中，零部件间刚度和阻尼参数的设置对仿真结果影响较大。为定义各零部件间的连接关系，在弹簧单元中不同方向上设定不同的刚度、阻尼值，主轴由2个轴承支承，轴承允许轴绕轴向旋转，给定沿X，Y方向上的刚度和阻尼值来限制其运动[15]；此外，滑靴紧贴于斜盘表面，可沿X，Y向平动及绕Z轴转动，故滑靴具有X，Y和RZ3个自由度，用CBUSH单元定义这3个方向上的刚度和阻尼值[15]；柱塞在柱塞孔内沿Z向平动及绕Z轴转动，具有Z,RZ2个自由度；缸体紧贴于配流盘表面绕Z轴旋转，具有转动自由度RZ。在模型中，分别在缸体和配流盘接触面上创建4处RBE3单元，再用CBUSH单元设定刚度、阻尼值使其连接[14]。对于法兰盘与壳体、壳体和端盖，用CELAS1单元模拟螺栓连接[15]。在装配体有限元模型中，假定每个螺栓沿X和Y方向的刚度相等。

搭建柱塞泵的装配体有限元模型后，求解了5000 Hz内的约束模态信息。在此频率范围内，共有45阶模态，由于零部件较多，一些模态为某些零部件的局部模态，这些模态对振动噪声的影响较小，不作为研究重点。本研究只关注对振动噪声影响较大的全局模态。表4为10阶全局模态的模态频率和振型描述，图6为前4阶全局模态振型图，x表示模态振动变形的位移。

图6 装配体有限元模型前4阶模态振型

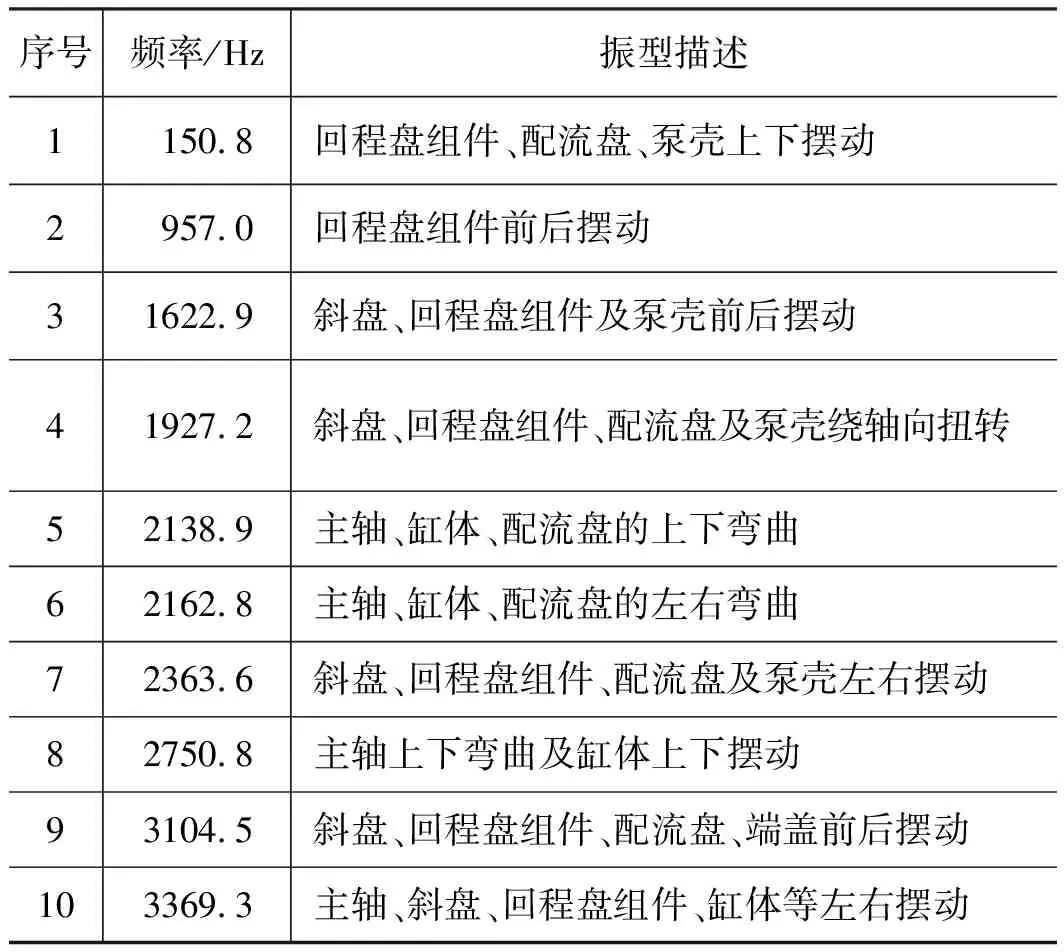
表4 柱塞泵装配体有限元模型主要模态频率及振型

3.3 振动响应分析及实验验证

基于所求轴向柱塞泵装配体结构模态，进行振动响应分析。在模型中定义了2个激振力的作用点，激励点1在回程盘组件的中心，激励点2在配流盘的中心。将所求频域下激振力施加在2个激振点上，进行基于模态的振动响应分析，得到各频率下振动速度云图，转换可得到云图上各节点振动幅频曲线。

为验证模型准确性，对轴向柱塞泵进行了振动测试，如图7所示。在壳体正上方法兰盘上布置测点1，在壳体左侧铣面中心布置测点2，在壳体上端面布置测点3，在端盖端面右侧布置测点4，在壳体右侧铣面中心布置测点5，在端盖端面中心布置测点6。

图7 振动测试试验台

由测试结果可知，3000 Hz内包含了轴向柱塞泵产生振动和噪声的振动幅值较大的频率，故给出了工况转速1500 r/min，对应出口压力14 MPa下，测点3沿Y方向上3000 Hz内振动速度v的仿真与实验对比图，如图8所示。

从图8可以看到，振动幅值出现在225 Hz及其倍频上，仿真结果值略大于实验测试值，但整体吻合较好，说明所搭建的轴向柱塞泵振声模型具有较好的精度，可以用于后续的仿真分析。

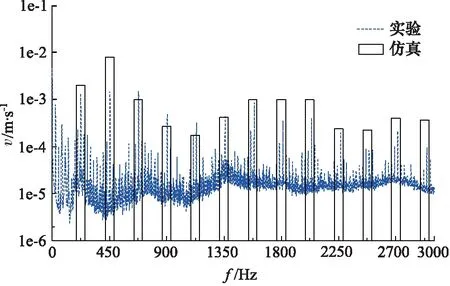
图8 仿真与试验振动速度对比

3.4 声学模型及辐射噪声分析

将轴向柱塞泵振动结果映射到声学包络面上，基于声学边界元模型进行辐射噪声分析。以轴向柱塞泵中心为原点，设置半径为1 m的半球包络面，在距中心垂直距离0.6 m处设置对称面以模拟地面反射，在端盖中心后方、轴向柱塞泵左、右两侧及中心上方设置4个场点，如图9所示。

图9 声学模型设置原理图

基于振动响应分析结果，求取3000 Hz内，225 Hz及其倍频下的声压级P，如图10所示。对比4个场点的声压级曲线，最大声压值出现在场点3的1350 Hz频率时，约为76.4 dB(A)，因此选择场点3作为目标场点。

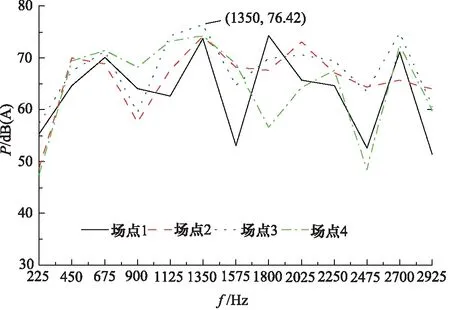
图10 辐射噪声声压级曲线

4 壳体降噪区域识别

4.1 声学传递向量分析

在声压波动较小时，通过声传递向量建立声场中某场点的声压与外表面的振动速度之间输入输出的线性关系，声场中场点r在角频率ω下的声压P(r,ω)为[19-20]:

P(r,ω)=MATV(r,ω)T·vn(ω)

(4)

式中，ω=2πf，f是频率；MATV(r,ω)表示声学传递向量；vn(ω)表示结构表面的法向振动速度。

由式(4)可知，声学传递向量、结构表面的法向振动速度(即结构模态振型)与场点声压直接相关。根据模型求解结果，对二者进行进一步分析。在计算轴向柱塞泵辐射噪声后，进行声学传递向量分析，得到在1350 Hz处，场点3所对应的声学传递向量云图如图11所示。

图11 声学传递向量云图

结合图11a和图11b可以看到，壳体上下端面和左右侧面为声学传递向量值较大的区域，因此选定这4个面为针对场点3降噪的区域面。

4.2 模态声学贡献量分析

除了声学传递向量，结构表面法向振动速度即结构模态振型对于场点声压的影响较大。将模态振型向量进行线性叠加可得到结构振动的结果。结构表面在法向方向上的振动速度由位移响应在法线方向上投影并求导后得到[20-21]:

(5)

式中，i——虚部单位

N——模态总阶数

qj(ω)——第j阶模态的模态参与因子

{φ}nj——第j阶模态在结构表面上的法向分量

结合式(4)及式(5)可得到在所求频域内声场中任意场点的声压P(r,ω)[20-21]：

(6)

式中，Psj(r,ω)表示第j阶模态产生的声压。

结构在激励下第j阶模态产生的声压在总声压中的占比为模态声学贡献量Cs。第j阶模态的声学贡献量Csj(r,ω)[20-21]：

(7)

式中，θp和θpj分别表示P(r,ω)和Psj(r,ω)的相位。

在确定声学传递向量较大的4个区域面后，进行模态声学贡献量分析。图12显示了场点3下，前45阶模态声学贡献量。可以看出在225 Hz及其倍频处声学贡献量都较大，其中在1350 Hz处出现贡献量最大值，约76.9 dB(A)。

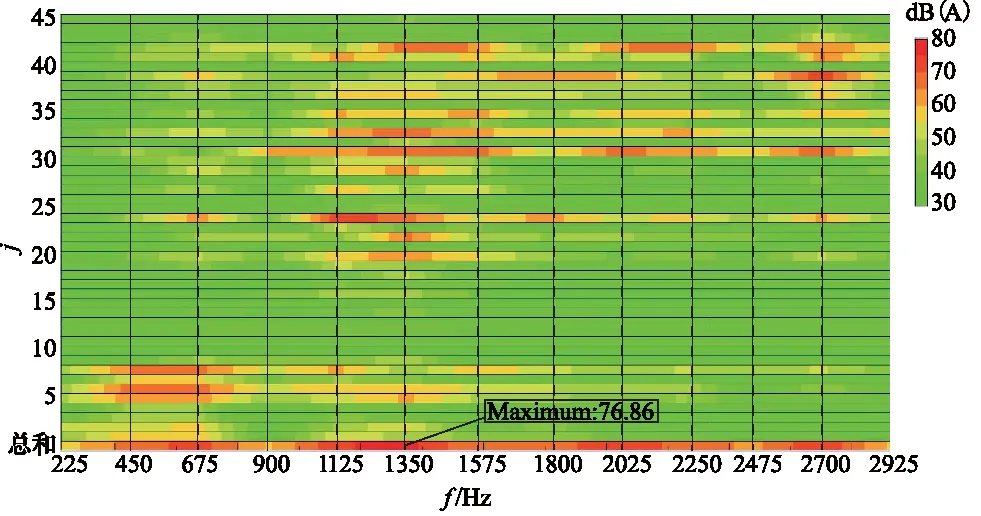
图12 前45阶模态声学贡献量

提取1350 Hz下贡献量较大的10阶模态声学贡献量，如图13所示。可以看出，正值声压贡献量较大的模态由大到小依次为22，20，29，24，6，37，42阶，其中22阶模态贡献量最大，约为14.9%。故将参考22阶模态振型，结合振型中法向振动位移较大的区域进行板面划分及板面贡献量分析。

图13 在1350 Hz下各阶模态声学贡献量

如图14所示，将22阶(即1927.2 Hz)模态振型映射到柱塞泵壳体表面上，基于声学传递向量的分析结果，提取22阶模态振型中上下端面及左右侧面共4个区域面。

图14 第22阶模态振型

4.3 板面声学贡献量分析

板面声学贡献量是结构在激励作用下某板面产生的声压在总声压中的占比。将式(6)中的MATV(r,ω)和{φ}nj展开，则声场中场点r在频率ω下的声压为[20-21]：

(8)

式中，k——网格的节点编号

U——节点总数

{φ}njk——第k个节点在第j阶模态在结构表面上的法向分量

Pk(r,ω)——第k个节点产生的声压

假设一个板面有L个节点组成，则该板面产生的声压Pc(r,ω)为[20-21]：

(9)

板面的板面声学贡献量Cc(r,ω)为[20-21]：

(10)

式中，θc表示Pc(r,ω)的相位。

结合图13和图14，基于声学传递向量、模态声学贡献量分析结果进行板面区域的划分。在明确降噪区域为壳体Pc(r,ω)上下端面、左右侧面的基础之上，进一步缩小降噪区域范围，确定板面划分区域如图15所示。

图15 板面划分区域

对图15中的4个板面区域进行板面声学贡献量分析。结果如图16所示，针对场点3在1350 Hz频率下的噪声水平，板面1，2，3，4的贡献量分别为-23.0%，46.1%，29.6%，1.3%，其中板面2的声学贡献量最大，对轴向柱塞泵辐射噪声的贡献最大。

图16 板面声学贡献量

5 结论

本研究建立了包含液压-多体动力学/有限元/边界元模型的轴向柱塞泵振声模型并通过锤击法模态试验及振动实验验证了有限元模型的准确性，基于振声模型开展了声学传递向量、模态和板面声学贡献量分析，得出以下结论：

(1)柱塞泵零部件模态试验结果的误差均小于5%，振动实验结果与仿真结果整体吻合较好；

(2)轴向柱塞泵壳体振动辐射噪声最大的位置场点3下，板面2在辐射噪声突出的1350 Hz频率时，其声学贡献量达到46.1%；

(3)本研究提出的方法可精确识别轴向柱塞泵壳体降噪板面区域，为其降噪优化设计提供有效指导。