液压马达变负载恒速控制动态特性对比

刘 杰

(1.中国煤炭科工集团太原研究院有限公司，山西 太原 030006；2.山西天地煤机装备有限公司，山西 太原 030006；3.煤矿采掘机械装备国家工程实验室，山西 太原 030006)

引言

在工程机械中，液压马达由于其功率密度比大、体积质量小、效率高等特点被广泛应用。特别是在行走机械中，液压马达用于旋转副的大扭矩传递，如挖机的回转液压马达、煤矿机械的行走马达和输送马达等[1-3]。

液压马达在工作过程中由于工况复杂性，其负载不断变化，马达泄漏增加会导致其速度产生波动，严重影响工作的稳定性和可靠性[4-5]。工程机械中有3种保持液压马达恒速工作的方法：变转速电机控制、阀控制、泵控制。3种不同的恒速控制方法具有不同的响应特性，在使用过程中往往只是通过经验选择恒速控制模型。对比研究3种马达调速方式的动态特性，有助于在不同工况或不同要求下选择不同的马达恒速控制模型。

1 液压马达恒速控制原理

1.1 变转速电机控制原理

图1为电机控制实现马达恒速的原理框图。初始状态下，输入信号到电机使其转动，带动定量泵工作。液压泵将电机的机械能转化为压力能，驱动液压马达转动工作，同时通过转速传感器将马达转速反馈到PID控制器。当液压马达所受负载增大时，由于泄漏损失增大等原因使其转速下降，此时通过PID控制器形成闭环，可自动改变电机的输入信号，调节转速，以使泵与马达实现流量自适应匹配。在此种马达恒速控制原理中，电机转速需不断变化以匹配变负载情况，因此需使用变频电机等变转速电机作为泵的驱动电机。

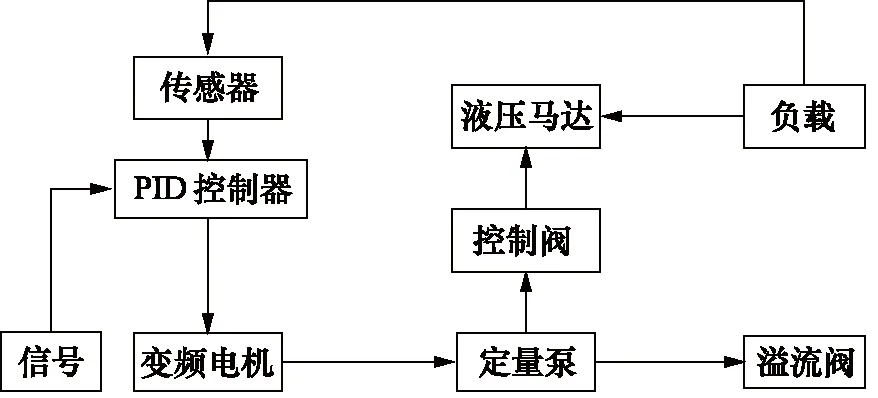
图1 变转速电机控制原理

1.2 阀控制原理

图2为阀控制实现马达恒速控制原理框图。初始状态下，恒速电机带动定量泵工作，压力油通过比例阀至液压马达，驱动液压马达转动工作，同时通过转速传感器将马达转速反馈到PID控制器。初始信号输入比例阀，使其提供一定流量以适应马达初始负载。当液压马达所受负载增大时，转速的下降反馈到PID控制器，使其自动改变比例阀输入信号，增大液压马达输入流量以弥补其损失。在此种马达恒速控制原理中，马达的输入流量需不断变化以弥补负载增大时的泄漏损失，因此需使用比例阀作为控制阀。

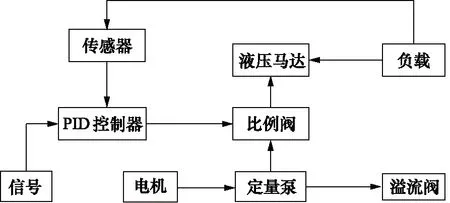
图2 阀控制原理

1.3 泵控制原理

图3为泵控制实现马达恒速控制的原理框图。初始状态下，初始信号输入电比例排量泵，此时泵以一定排量工作。恒速电机带动电比例排量泵转动，压力油流至液压马达，驱动液压马达转动工作，同时转速传感器将马达转速反馈到PID控制器。当液压马达所受负载增大时，转速下降信号反馈到PID控制器，通过与初始信号对比，自动改变泵的输入信号使其变排量，以实现泵与马达的流量自适应匹配。此种马达恒速控制原理中，泵的排量需要随输入信号不断变化，因此需使用电比例排量泵作为液压动力元件。

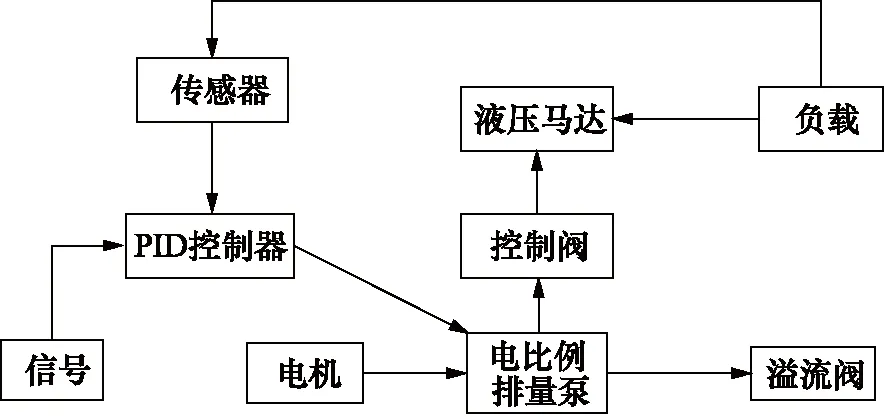
图3 泵控制原理

2 液压马达恒速控制数学模型

2.1 变转速电机控制数学模型

假设变转速电机为永磁同步电机，由文献[6-7]可知，永磁同步电机的电磁转矩为：

Te=1.5PnIssinβ(ψf+Ld-LqIscosβ)

(1)

式中，Te——电磁转矩，N·m

Pn——电机的极对数

Is——定子电流空间向量，A

β——定子电流空间向量与两相旋转标系d-q轴中d轴的夹角，rad

ψf——转子的磁链，Wb

Ld——两相旋转坐标系d轴电感，H

Lq——两相旋转坐标系q轴电感，H

电机的机械运动扭矩方程为：

(2)

式中，TL——电机负载转矩，N·m

Jem——电机转动惯量，kg·m2

ωe——电机角速度，rad/s

Bem——电机的阻尼系数，N·m·s/rad

伺服控制器的输入电压与电机角速度成比例关系，则有：

ωe=kuei

(3)

式中，k——转换系数，rad/(s·V)

uei——伺服控制器输入电压，V

电机与泵连接，则有扭矩平衡方程：

(4)

式中，Dp——泵的排量，m3/r

pp——泵的输出压力，MPa

Bp——泵的阻尼系数，N·m·s/rad

ωp——泵的角速度，rad/s

Jp——泵的转动惯量，kg·m2

泵的流量方程为：

Qp=Dpωp-CipΔpp-Coppp

(5)

式中,Qp——泵输出的流量，m3/s

Cip——泵的内泄系数，m5/(N·m)

Δpp——泵进出口压差，MPa

Cop——泵的外泄系数，m5/(N·m)

马达的流量方程为：

(6)

式中,Qm——马达的输入流量，m3/s

Dm——马达排量，m3/r

θm——马达的转角，rad

Cim——马达的内泄系数，m5/(N·m)

Δpm——马达进出口压差，MPa

Com——马达的内泄系数，m5/(N·m)

pm——马达高压腔的压力，MPa

V0——马达高压腔体容积，m3

βm——马达有效容积的弹性模量，N/m2

马达在外负载的作用下有力矩平衡：

(7)

式中,Jm——马达负载转动惯量总和，kg·m2

Bm——马达和负载的阻尼系数和，

N·m·s/rad

G——马达外负载弹簧刚度，N·m/rad

T′——施加在马达上的外负载，N·m

由于此种控制模式中，电机角速度等于泵的角速度，泵的输出压力等于马达高压腔的压力，泵的输出流量等于马达的输入流量，即有：

(8)

同时联立式(1)～式(7)即为变转速电机控制马达转速的数学模型，此处不再赘述。

2.2 阀控制数学模型

阀控制马达机转速的最大特点是需使用比例阀，由文献[8-12]可知，比例阀的流量方程为：

Qv=Kqxv-Kcpv

(9)

式中,Qv——比例阀输出流量，m3/s

Kq——比例阀的流量增益，m3/(s·A)

xv——阀芯的位移，m

Kc——压力流量比例系数，m5/(N·s)

pv——比例阀输出压力，MPa

比例阀输入电流与阀芯位移之间的关系为：

(10)

式中,KI——比例阀的电流力增益系数，N/A

ivi——比例阀的输入电流，A

mv——阀芯的质量，kg

mT——衔铁的组件质量，kg

Bv——阀芯与衔铁间阻尼系数，N·s/m

BT——衔铁组件的阻尼系数，N·s/m

kv——综合刚度，N/m

此种控制模式中，马达输入流量等于比例阀输出流量，即有：

Qm=Qv

(11)

同时联立式(6)、式(7)即为阀控马达转速的数学模型，此处不再赘述。

2.3 泵控制数学模型

泵控马达转速与阀控马达转速的不同在于，阀控系统由比例阀直接控制马达的输入流量，泵控系统则由比例阀控制变量活塞，同时可带动变量泵斜盘倾角的变化，从而改变泵的排量以实现与马达负载的匹配，如图4所示。因此，建立泵控马达转速的数学模型，除了前述的公式外，还需泵变量活塞和斜盘等的数学模型公式。

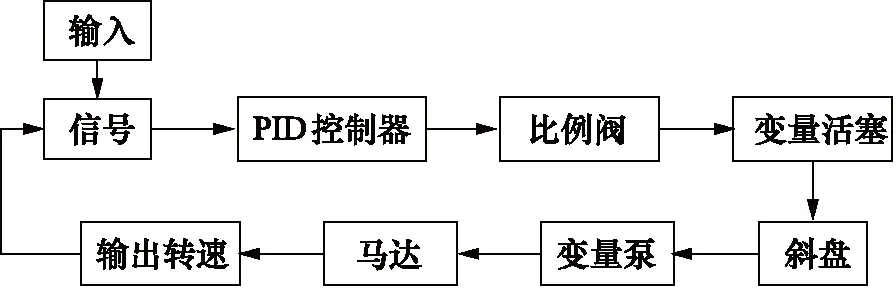
图4 泵控控制框图

变量活塞为双作用的对称液压缸，因此油缸的力平衡公式为：

(12)

式中，Ac——双作用缸有效面积，m2

Δpc——双作用缸两腔体压力差，MPa

mc——双作用缸及负载总质量，kg

y——双作用缸的位移，m

Bc——双作用缸与负载阻尼系数，N·s/m

K——双作用缸与负载弹簧刚度，N/m

Fc——双作用缸负载力，N

双作用缸的流量平衡公式为：

(13)

式中,Qc——双作用缸负载流量，m3/s

Cic——双作用缸泄漏系数，m5/(N·m)

Vc——双作用缸容积和，m3

βc——双作用缸综合的弹性模量，MPa

双作用缸的位移与斜盘之间的转换关系为：

y=Lα

(14)

式中，L——双作用缸到斜盘铰点距离，m

α——斜盘的倾角，rad

在此种控制模式中，比例阀输出压力等于双作用缸两腔体压力差，即有：

pv=Δpc

(15)

同时联立式(5)～式(7)、式(9)、式(10)即为泵控马达转速的数学模型，此处不再赘述。

分析上述的数学模型可以发现，泵控比阀控多了变量活塞及斜盘的中间环节，控制流程增多，控制更精确，可以预测泵控的响应时间会比阀控时间长，泵控的超调量会比阀控小。变转速电机控制由于控制多元复杂性无法预测，可通过实验进行进一步验证。

3 实验与分析

为了分析3种马达恒速控制的动态响应，使用山西天地煤机的加载实验台进行实验。

针对马达工作时的变负载工况，采用加载马达对实验马达进行加载实验，加载实验原理如图5所示。通过泵和马达选型匹配及PID控制，以马达转速1500 r/min为优化目标进行实验。在加载马达出口安装比例溢流阀来调节加载压力pLoad。加载工况曲线如图6所示。可以看到，初始加载压力为5 MPa，在第2.5秒加载压力突变为10 MPa，并在2.5 s后恢复为5 MPa，如此反复分别加载10, 15, 20 MPa 3种压力等级。

图5 加载实验原理图

图6 马达加载压力

图7为变转速电机马达恒速控制的动态响应曲线，在每一次加载压力切换时，由于压力冲击等原因使马达转速存在上下波动，且压力阶跃值越大，电机的转速波动幅值越大，PID控制的超调量越大。在此种控制下，马达在变负载时可以实现快速的恒速调节，但整体控制不太平稳，转速波动次数较多。

图7 变转速电机控制动态响应

图8为阀控马达恒转速控制的动态响应曲线，在每一次加载压力切换时，在压力冲击的作用下也会导致马达转速上下波动。PID控制的超调量较大，但响应速度较快，可以实现马达变负载下转速的快速回正。

图8 阀控动态响应

图9为泵控马达恒转速控制的动态响应曲线，在加载压力切换时，马达转速上下波动，加载压力与波动幅值正相关。在PID控制调节下，马达转速可恢复为1500 r/min，且整体控制相对比较平稳，超调量小。与此同时，泵控马达恒转速控制的响应时间较长，大于变转速电机和阀控系统。

图9 泵控动态响应

将3种控制模式的最大超调量ζ汇总对比，如图10所示。阀控系统最大超调量在3种加载压力下均为最大，泵控系统的最大超调量最小，且这种特征在15 MPa时最为明显，在加载压力值为10 MPa和20 MPa时，变转速电机控制与泵控系统最大超调量接近。

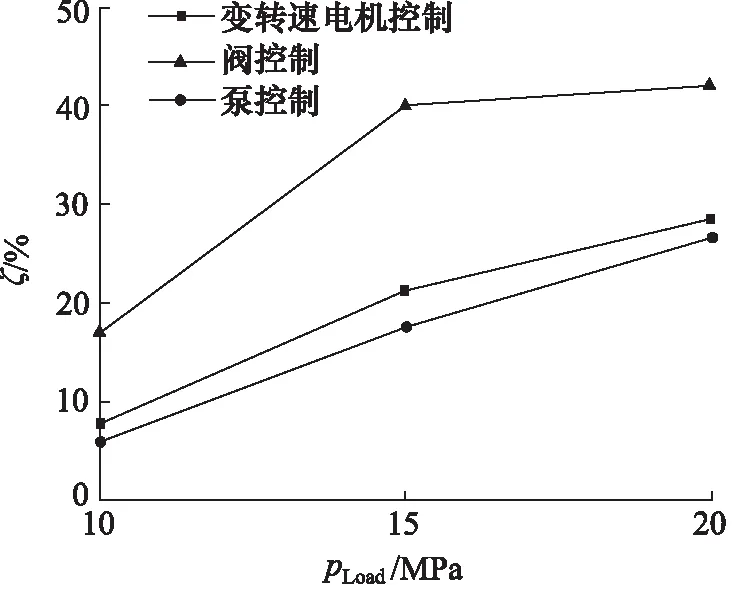
图10 最大超调量对比

将3种控制最大超调量的上升时间tr汇总，如图11所示。阀控系统上升时间在3种加载压力下均为最小，泵控系统的上升时间最大，变转速电机上升时间处于两者中间。

图11 最大上升时间对比

分析以上3种控制方式的最大超调量、上升时间可以发现，实验结果与数学模型中的预测结果相同。

以上结果可以指导在不同工况和工作条件下选择合适的马达转速控制方法。当系统要求马达调速响应快而对转速波动敏感度较低时，可以选择阀控调速；当系统要求控制平稳而对响应时间无过大要求时可以选择泵控系统；当工况普通无过多要求时变转速电机控制是较好的选择。

4 结论

本研究通过数学模型构建、实验验证等方法对液压马达变负载恒速控制的3种方法——变转速电机控制、阀控制、泵控制的动态特性进行比较分析，结论如下：

(1)阀控系统响应时间快，超调量大；泵控系统响应时间慢，超调量小，调速平稳；变转速电机控制的特性处于两者之间，但调速不太平稳，波动次数多；

(2)可根据以上调速特性针对不同的工作情况选择不同的调速方式，本研究为PID控制器在3种控制方式上的应用研究，也可探究模糊控制、神经网络控制等智能控制在3种调速方式的响应特性区别。