变工作条件下齿轮泵特性分析
王霞琴,邓 龙,柴红强,曹川川
(1.兰州石化职业技术大学 机械工程学院,甘肃 兰州 730060;2.兰州理工大学 能源与动力工程学院,甘肃 兰州 730050)
引言
作为流体动力系统的能量转换元件,齿轮泵(特别是内啮合齿轮泵)具有结构紧凑,自吸性能高,抗污染性强,使用寿命长等特点,广泛应用于采矿行业、冶金行业、船舶工程等领域[1]。
实际液压系统中由于环境条件变化的随机性、液压传动装置中部件布置的复杂性以及人为操作与维护保养的规范性等,很多因素会导致齿轮泵的工作条件始终处于动态演变过程[2-4]。变化的工作条件使得工作介质的基本属性产生重大改变,进一步导致齿轮泵流动特性发生变化。
基于流量连续性方程的集中参数模型可快速获得齿轮泵的流动特性,其原理是首先将齿轮泵内部流道划分为若干个控制体,然后根据相应的控制方程建立对应的流量模型,最后在商业软件LMS AMESim中建立了整泵的集中参数模型[5-7]。然而,采用集中参数法求解物理变化时,系统中各变量被认为是均布的,无法体现与空间位置的变化规律。
一些学者在考虑油液相关特性的条件下,对齿轮泵二维内部流场进行了瞬态仿真分析[8-9]。可是,二维内流道模型无法反映齿轮泵整体特性,同时这些研究并未分析齿轮泵用油的实际情况,也未指出齿轮泵流动特性随工作条件的变化规律。另外,RUNDO M[10]详细对比了近些年所采用的集中参数模型和分布式参数模型的特点及应用范围。然而,仅仅基于运动流量的研究忽略了流体黏度和压缩性对齿轮泵工作的影响,更无法反映流体质点的运动空间。
1 内泄漏数学模型
内泄漏不仅会降低输出容积效率,同时其不均性还会增大出口流量脉动率。齿轮泵内部泄漏流量有轴向间隙及径向间隙2个途径(由于啮合齿面间的泄漏非常少,因此不予考虑),内部泄漏实体模型见图1。
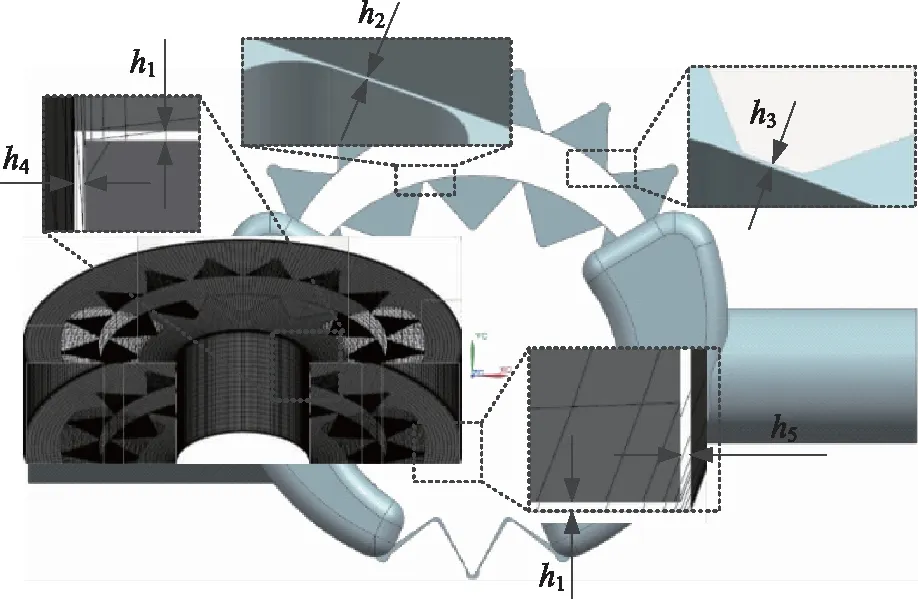
图1 齿轮泵内部泄漏实体模型
1.1 轴向间隙泄漏流量
根据压力大小分布将齿轮端面划分为同低压腔接触的区段,同高压腔接触的区段以及高低压腔之间的过渡区段3个部分,见图2。
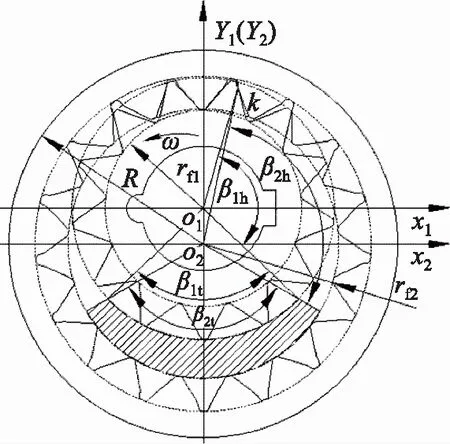
图2 轮齿端面区域划分图
基于轴向油膜结构特征,采用平行圆盘间隙流动理论来计算其中的泄漏流量,可得齿轮端面间隙中的泄漏量:
(1)
式中,h1——端面油膜厚度
R——内齿圈外壁半径
r——外齿轮内壁半径
Δp——压差
μ——油液动力黏度
rf1——外齿轮齿根圆半径
rf2——内齿圈齿根圆半径
β1h——外齿轮对应的高压腔包角
β2h——内齿圈对应的高压腔包角
β1t——外齿轮对应的低压腔包角
β2t——内齿圈对应的低压腔包角
1.2 径向间隙泄漏流量
由于齿顶油膜厚度远小于齿顶圆直径,其层流运动按照平行平板间隙流动理论来计算,因此可得外齿轮齿顶与月牙隔板间的泄漏流量:
(2)
式中,h2——外齿轮齿顶油膜厚度
B——齿宽
Se1——外齿轮齿顶厚度
ra1——外齿轮齿顶圆半径
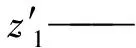
n1——外齿轮转速
同理可得内齿圈齿顶与月牙隔板间的泄漏流量:
(3)
式中,h3——内齿圈齿顶油膜厚度
Se2——内齿圈齿顶厚度
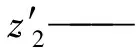
ra2——内齿圈齿顶圆半径
n2——内齿圈转速
由于外齿轮内壁与轴颈之间无相对运动,径向间隙泄漏可看作同心环缝在压差作用下的油液流动,因此可得泄漏流量:
(4)
式中,h4——外齿轮内壁油膜厚度
d——外齿轮内壁直径
e——轴颈深度
内齿圈外壁与壳体间的径向间隙泄漏根据平行平板间隙流动理论来计算,因此可得泄漏流量:
(5)
式中,h5——内齿圈外壁油膜厚度
2 正交试验设计
正交试验方法是利用正交表科学地安排与分析多因素的研究手段。该方法主要包括试验目标选择、因子-水平表确定、正交试验方案设计以及试验结果统计分析等步骤。
2.1 因子-水平表
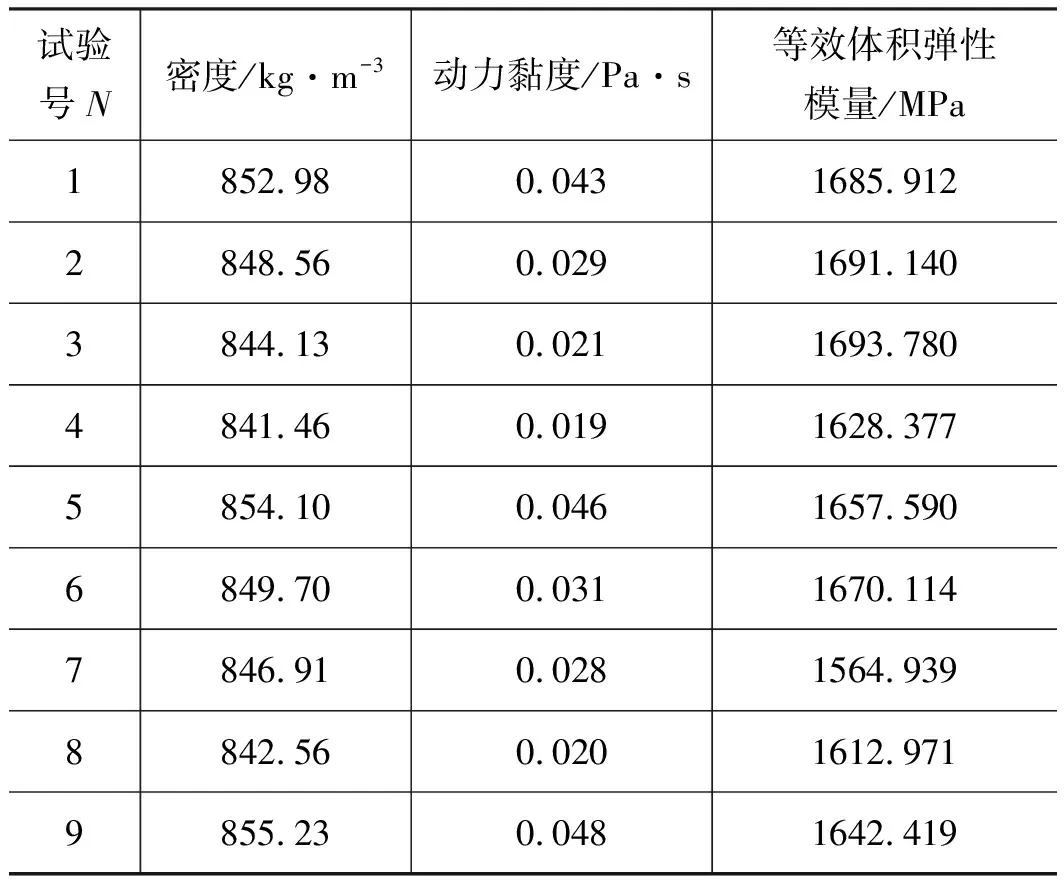
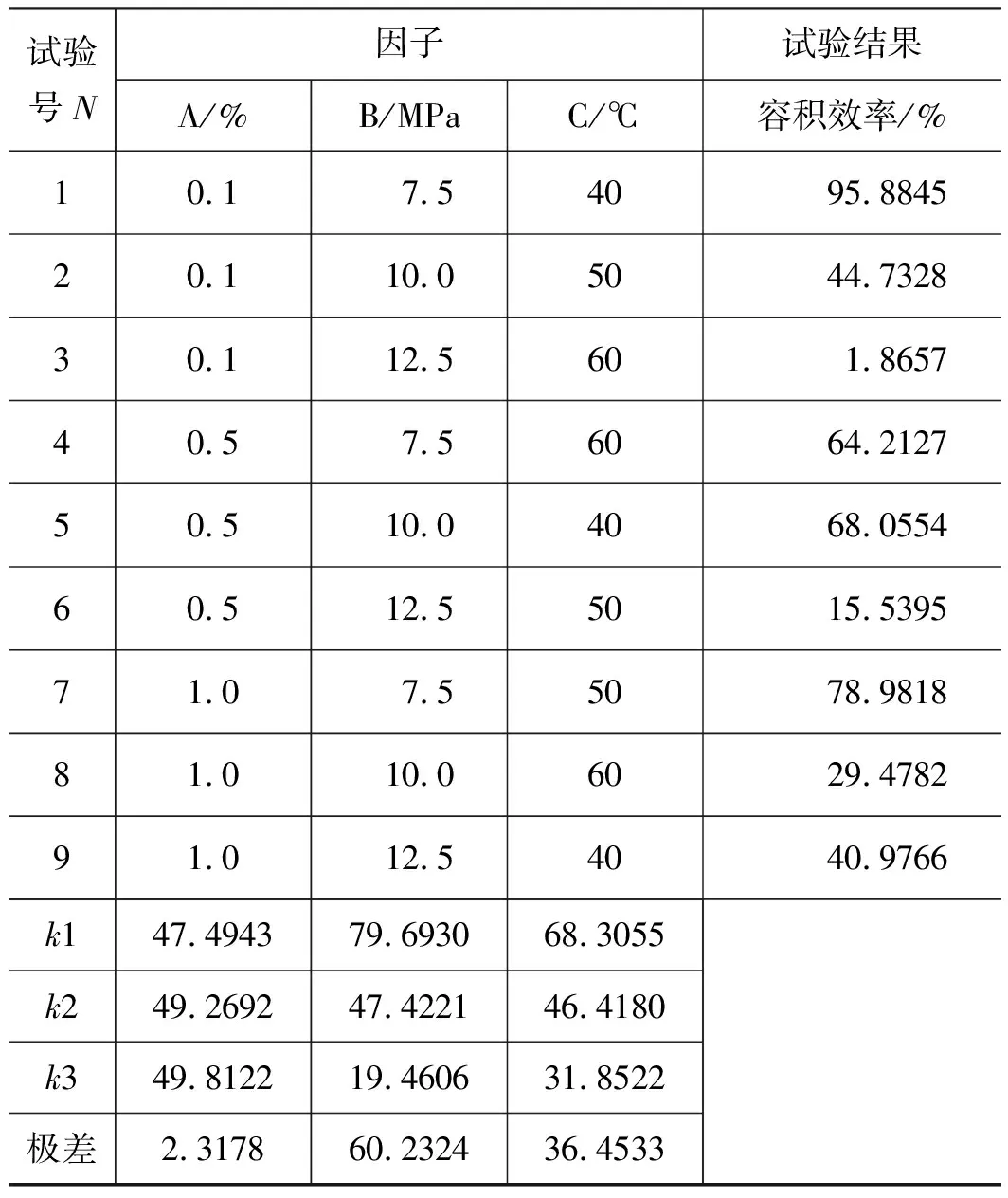
齿轮泵实际运行中工作条件一直处于变动过程,其为多因素、多水平的实际工况。因此确定可变的因子有:游离气体含量A、工作压力B及工作温度C等,同时假定A的水平取值分别为0.1%,0.5%,1%,B的水平取值分别为7.5,10.0,12.5 MPa,C的水平取值分别为40,50,60 ℃,如表1所示。
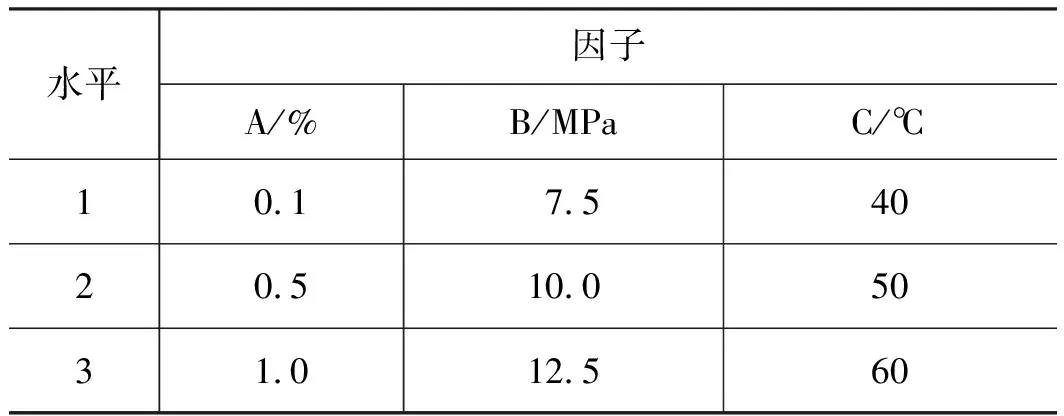
表1 正交试验因子水平表
2.2 正交试验方案
设计了L9(33)的正交表,可得9个具体的试验条件,对应的试验方案见表2。
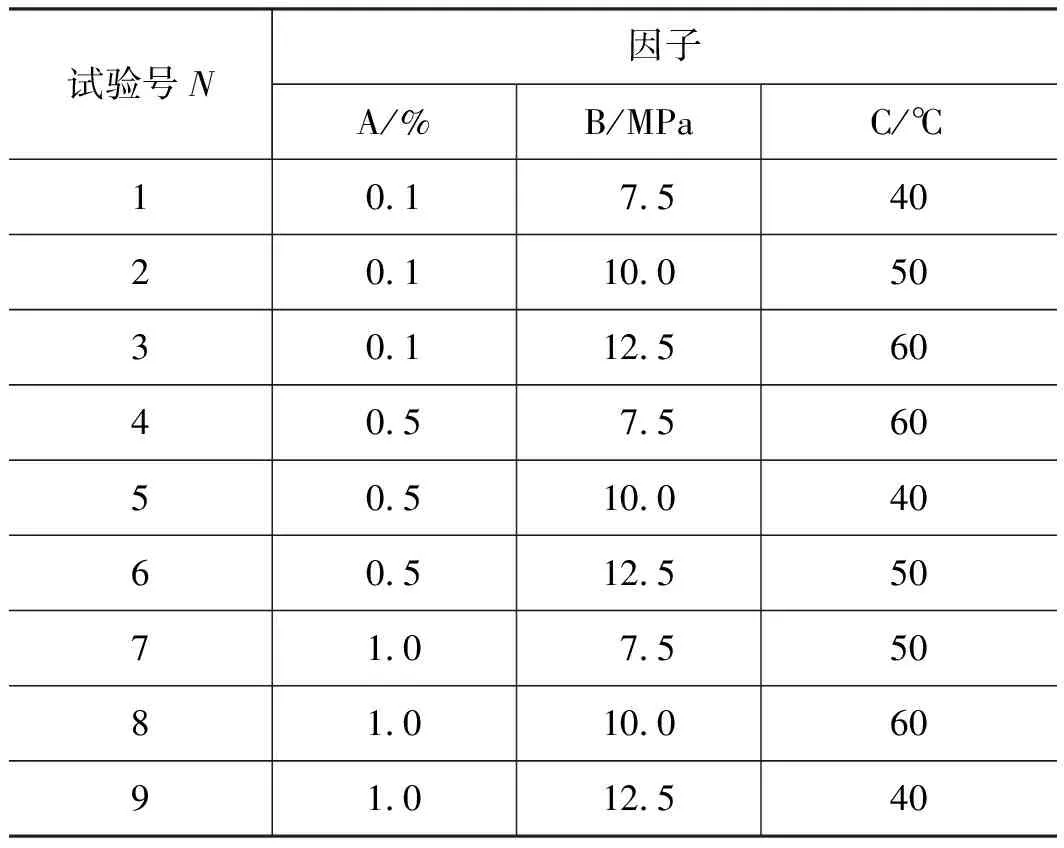
表2 正交试验方案
2.3 正交试验目标
为了全面分析不同工作条件对齿轮泵流动特性的影响,本研究选择的试验目标有流量脉动、压力脉动、容积效率及总效率。
3 CFD仿真模型
CFD问题的求解过程已经规范化[11],鉴于软硬件条件的多样性、CFD仿真程序的复杂性以及求解过程的稳定性等,CFD计算比较适应于商用软件[12],人为操作过程主要有以下几个方面。
3.1 三维内流道有限元模型建立
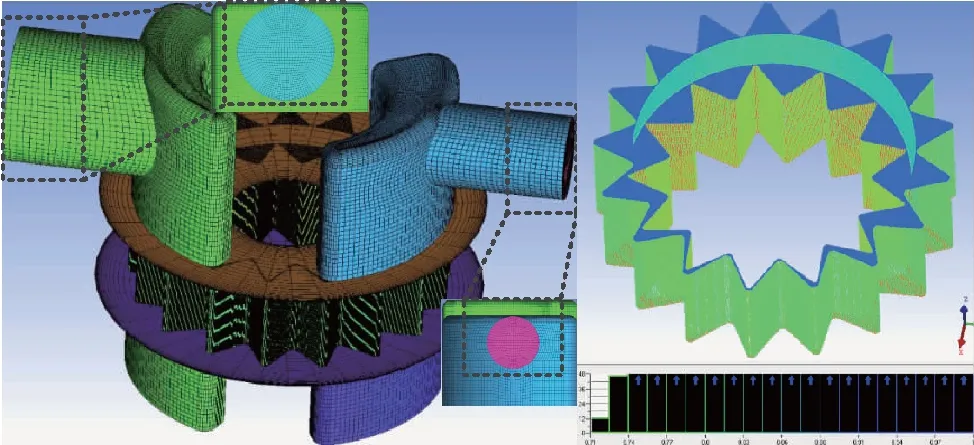
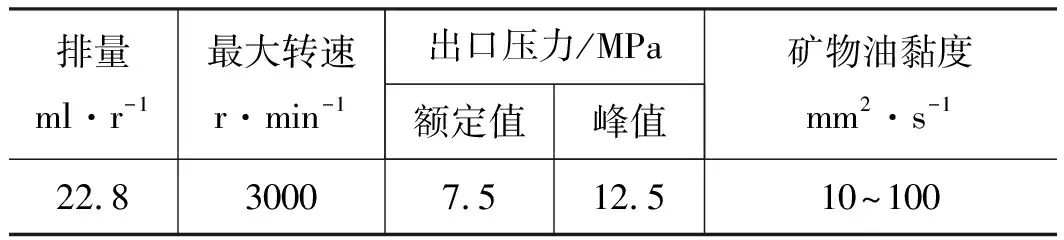
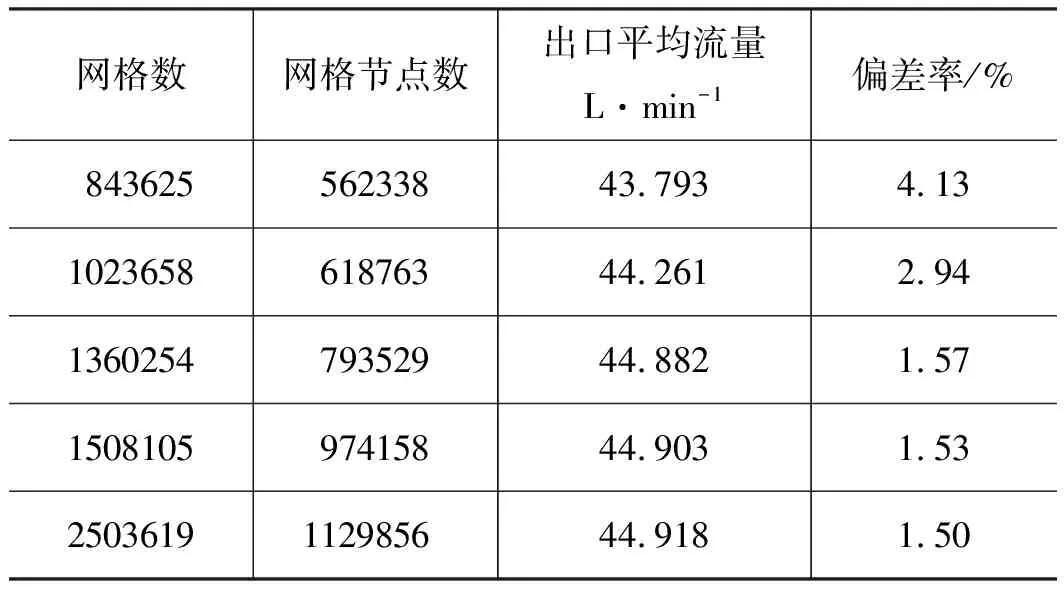
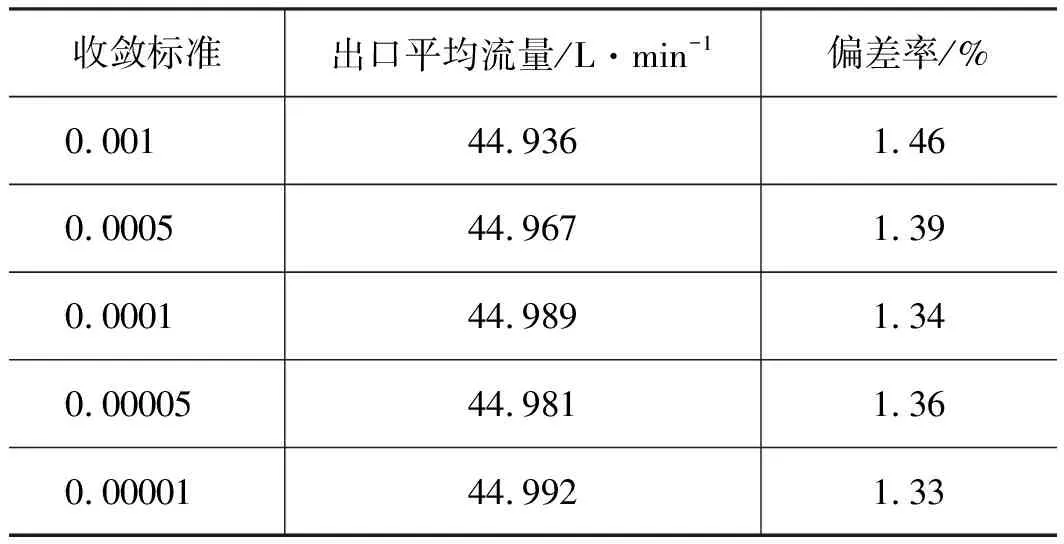
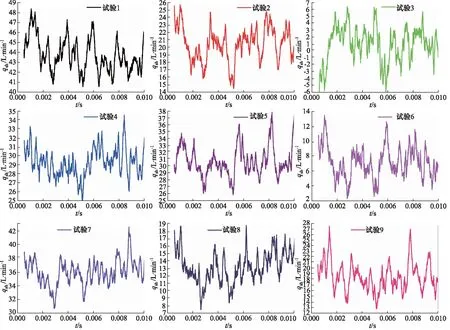
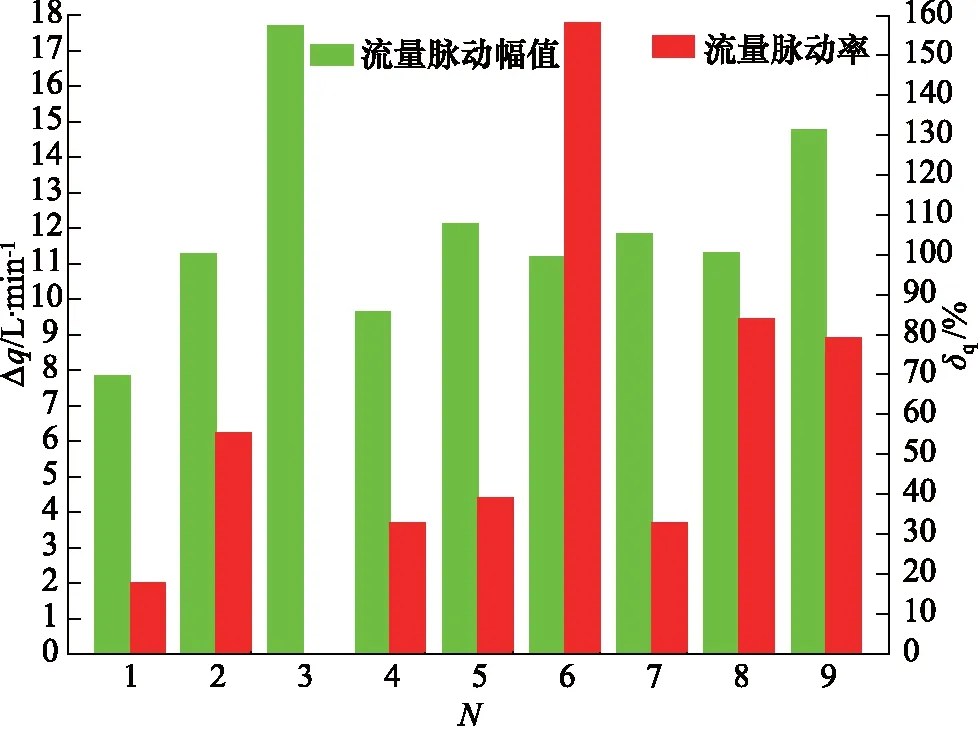
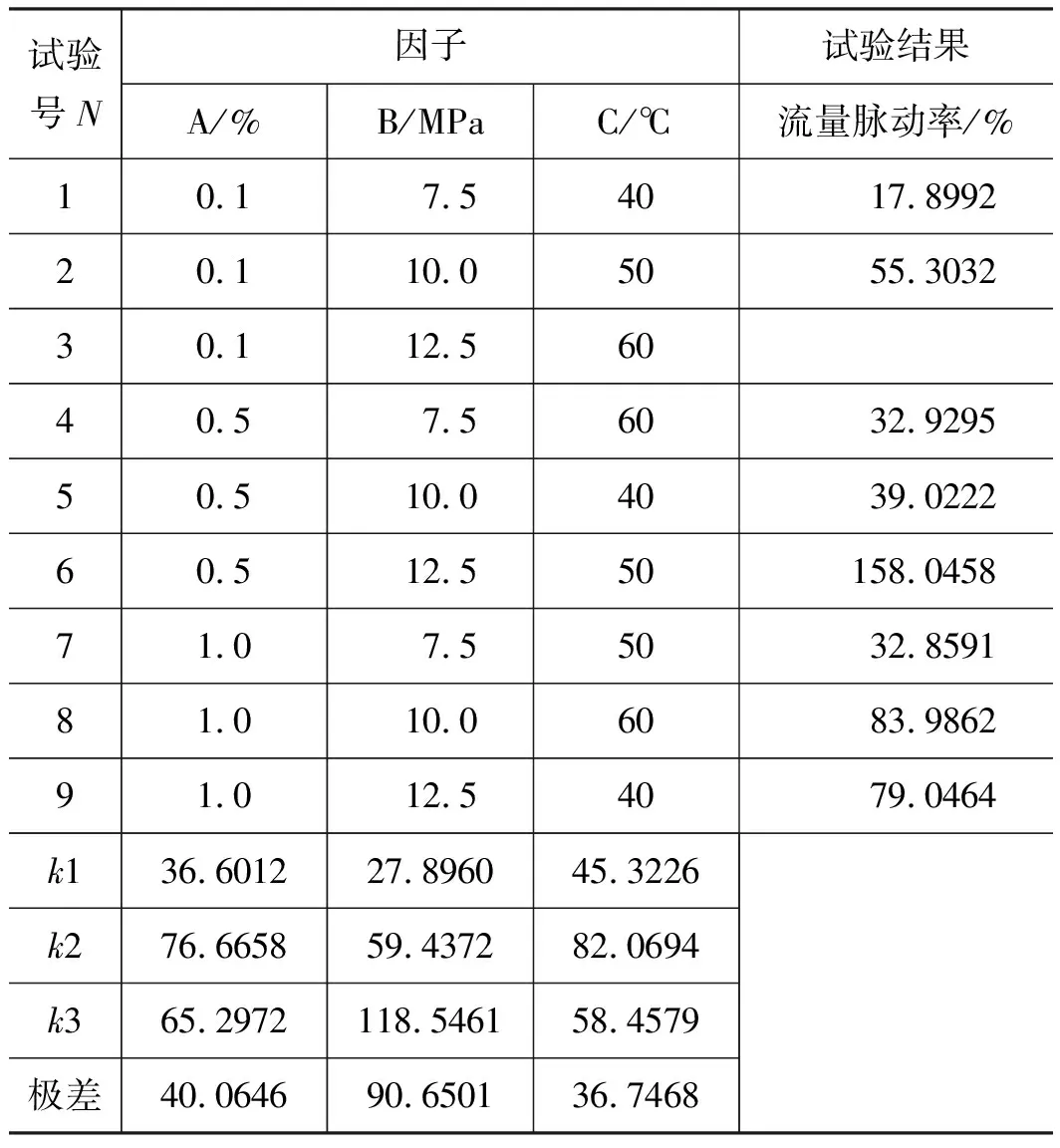
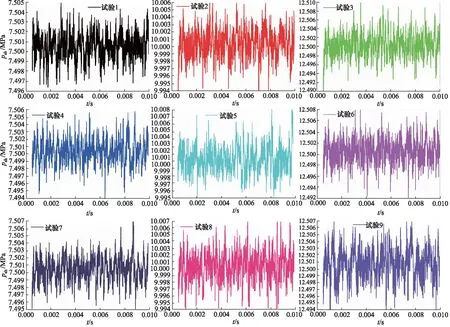
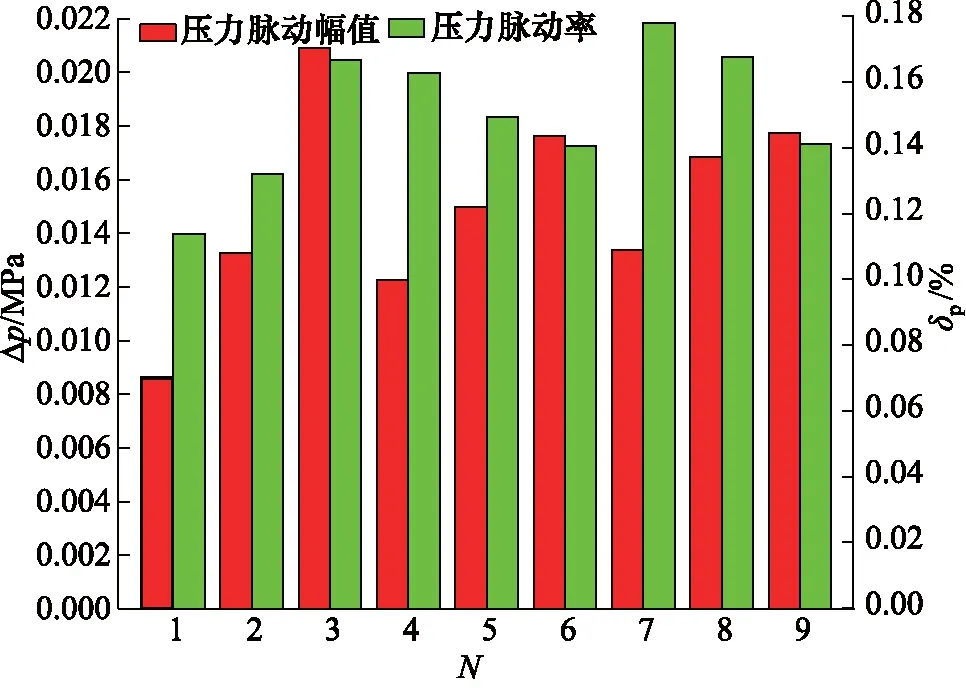
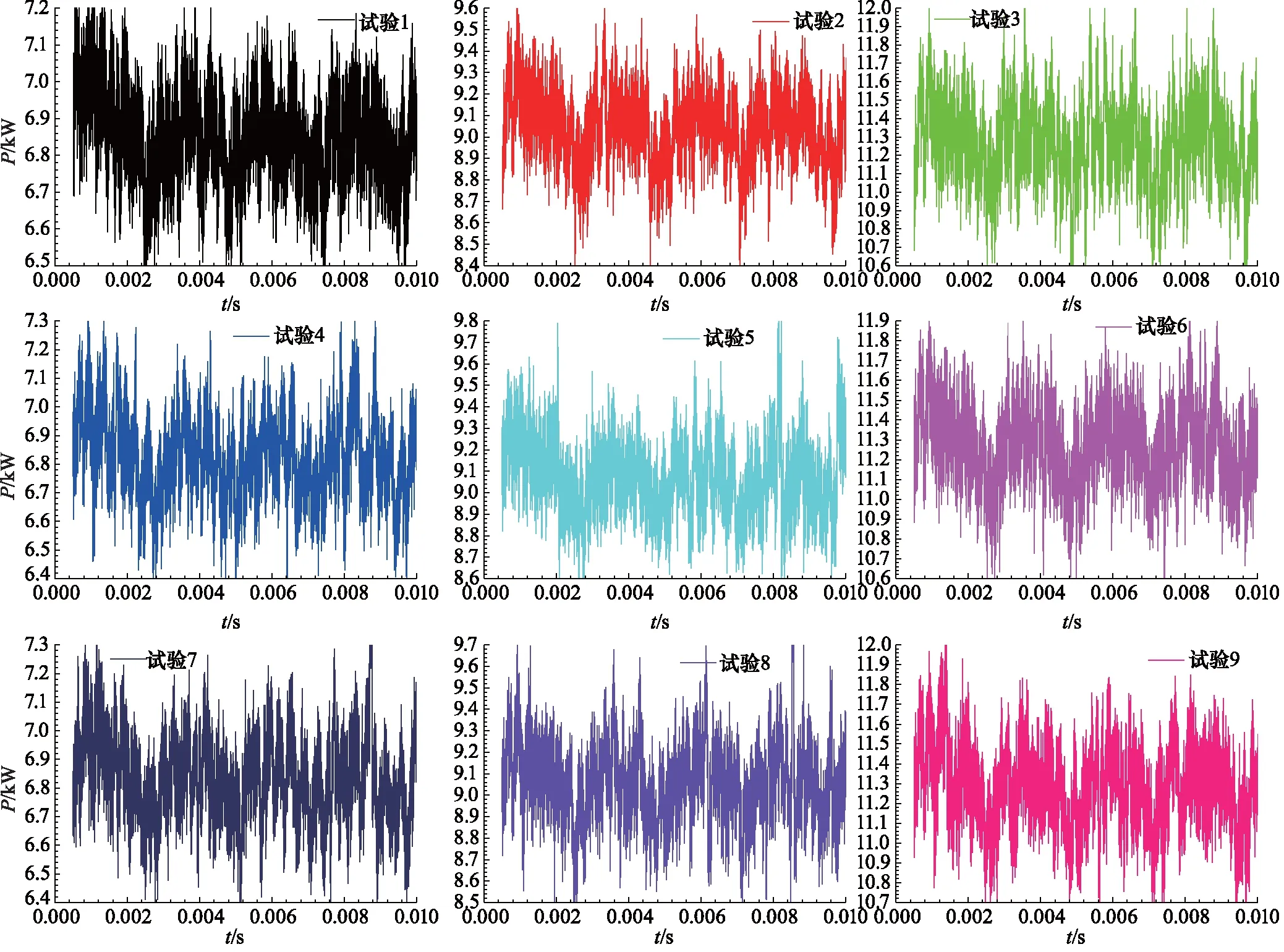
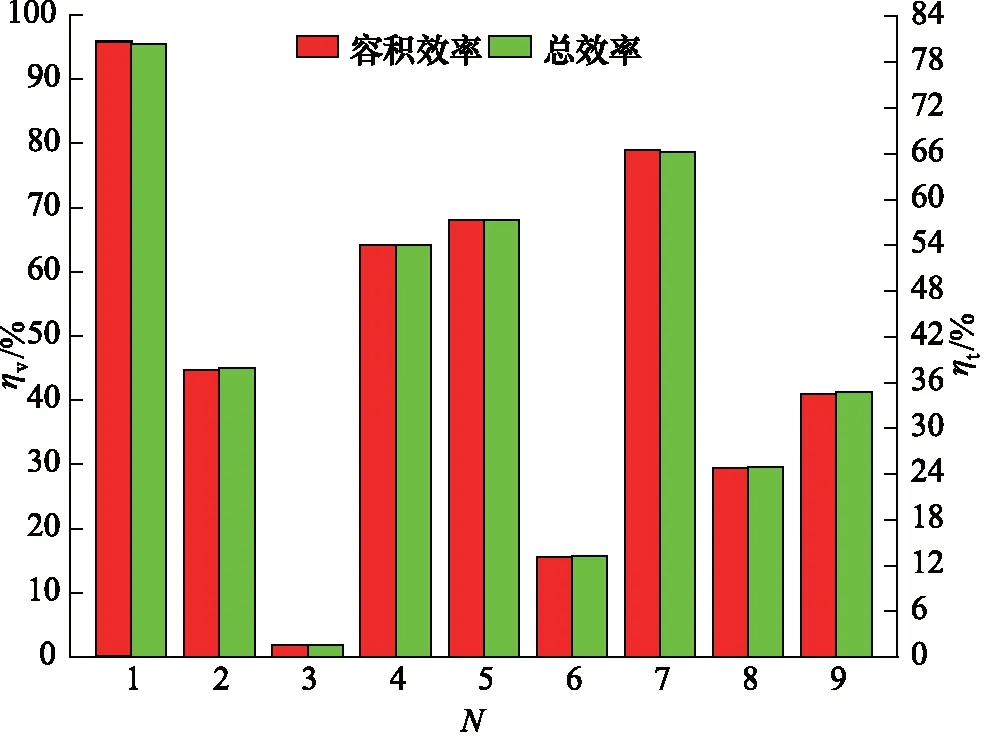
齿轮泵内部的3对摩擦副之间由一定厚度的油膜分隔开来,从而实现密封、润滑及传递作用力的功能。根据静压支撑特性理论、机床加工能力以及油液过滤精度等因素共同确定油膜厚度h的取值范围,0.02 mm 齿轮泵内部泄漏途径包括轴向、径向及齿面接触啮合油膜。在正常啮合的情况下,啮合齿面之间的油膜厚度非常薄,通过此处的泄漏非常少。因此,为了准确模拟内部实际泄漏,在考虑油膜厚度的条件下建立齿轮泵三维内流道模型。综合油膜中网格数量,具体油膜厚度设置如下:轮齿两端面与泵体之间、齿顶与月牙隔板之间都设定为0.1 mm,初始啮合齿面间设定为0.02 mm,具体的内流道三维实体模型见图3。 1.出口流道 2.进口流道 3.上轴向油膜 4.齿轮副流道 5.下轴向油膜 6.出口配油流道 7.进口配油流道 根据流体运动的边界层理论,非直接数值模拟仅适用于湍流流动,在黏性力主导的层流底层会失效。因此,数值计算过程中采用壁面函数来处理第一层网格节点的位置。 (6) 式中,τw——壁面切应力,τw=0.5Cfρμ2 ρ——流体密度 u——流体速度 Re——雷诺数 y+——无量纲壁面系数 经计算第一个节点到壁面距离的取值范围为0.05~0.5 mm。因此,本研究以0.2 mm的首层距离进行结构网格划分,具体的三维内流道有限元模型见图4。 图4 齿轮泵三维内流道有限元模型 为了使仿真过程中网格能够成功更新,对静态区域采用结构化网格进行划分,而动态区域采用非结构化网格进行划分,同时保证结构网格质量高于0.45,非结构网格质量高于0.71。 1)边界条件 CFD问题的边界条件指计算域边界上给定求解变量或其一阶导数随空间坐标及时间的变化规律。作为液压系统中的动力元件,齿轮泵进口与出口压力是已知且关键的。因此,选取压力作为进、出口边界条件,同时设定每组试验条件对应的含气量及油温,如表2所示(所有进口压力都设定为0 MPa)。 三维内流道中外齿轮及内齿圈对应的壁面都为周期性的运动壁面,需要编写对应的UDF同时设定动网格全局及局部参数来模拟其动作过程,其余静止壁面速度都设为0 m/s。 2)流动介质 根据齿轮泵用液压油的黏度范围及工作条件,选取46#矿物油作为工作介质,分别计算出每组试验条件对应的油液基本属性,即油液密度、动力黏度及等效体积弹性模量,如表3所示。 表3 不同试验对应的介质属性 3)两相流模型 由边界条件的定义可知,每次试验都设定气体体积分数、工作压力及工作温度,这样数值计算时必须开启能量方程及两相流模型。两相流模拟采用Mixture模型。由于整个内部流道中气体含量很低,可忽略油液与气体的速度差异,同时开启Implicit Body Force。另外,为提高计算稳定性,以空气为主相,同时设定气泡直径为0.01 mm。 4)时间步长 时间步长对于求解的稳定性、计算过程的时效性、物理量细节特征的捕获以及动网格的成功更新等起着至关重要的作用,因此综合各方面因素选择定时间步长,同时设定其值为1e-5 s。 为保证每个时间步内数值计算结果在给定标准下全部收敛,最大迭代次数设定为200。进一步获取该类型齿轮泵工作参数,见表4。 表4 齿轮泵工作参数 根据表4确定外齿轮转速为2000 r/min,根据传动比17/13可得内齿圈转速为1529.4 r/min,进一步计算齿轮泵运动周期为0.03 s。 5)湍流模型 齿轮泵工作过程中,由于齿轮副的啮合传动及高压差作用,容腔中油液速度及方向不断发生剧烈变化。经计算流动油液的雷诺数为9120,内部流动属于湍流运动。因此采用非直接数值仿真中Reynolds平均法求解时均化的Navier-Strokes方程,确定RNGk-ε涡黏模型来模拟内部湍流。 网格作为内流道模型的表现形式,同样也是数值计算及结果分析的基础,对于求解过程的稳定性及计算结果的准确性有着非常重要的影响。收敛标准控制着每个时间步内迭代计算精度,进一步影响整个流场计算结果的准确性。因此,为了尽可能消除人为因素对模拟结果的影响,需进行无关性验证。 1)网格无关性验证 由图2可知,三维内流道有限元模型的网格质量良好。因此只需验证网格节点增加到一定程度后对计算结果的准确性基本无影响。本研究对比了5组网格节点数对应的出口平均流量,如表5所示。 表5 不同网格节点数对应的出口平均流量 由表5可知,节点数增大至79.35万时,偏差率降低至2%以内,且随着网格数量的增加,偏差率基本维持不变。因此,为加快计算,选择节点数为79.35万的有限元模型。 2)收敛标准无关性验证 瞬态问题中默认的残差收敛标准为0.001。为进一步验证收敛标准继续降低后出口平均流量基本不再变化,本研究设置了5组收敛标准,分别为0.001,0.0005,0.0001,0.00005,0.00001,对应的出口平均流量如表6所示。 表6 不同收敛标准对应的出口平均流量 表6中,每个时间步内的不同收敛标准对出口平均流量的影响非常小。因此,为了提高计算效率,设置残差收敛标准为0.0001。 齿轮泵出口瞬时流量总是脉动的,究其原因是齿轮副运动过程中啮合点位置发生周期性变化产生几何流量脉动,不均匀内泄漏、油液压缩性及困油现象等造成工作流量脉动。几何流量脉动与工作流量脉动的结合导致出口流量的脉动性。因此,分别获取不同试验对应出口瞬时流量qsh曲线,如图5所示。 图5 不同试验条件下出口瞬时流量曲线对比 需要说明的是,由于运动周期内啮合点位置变化的周期性,进而造就齿轮泵流动特性的周期性。另外,鉴于求解基于动网格技术两相流模型的时效性及稳定性等,本研究提取约1/3周期(即0.01005 s)内的仿真数据进行分析。 由图5可知,在0~0.01005 s的时间内,瞬时流量曲线都是脉动的且全部呈现连续周期性变化,同时有约4个起伏脉动,原因是齿轮泵进口的油液通过齿轮副的啮合传动进行运输,在1/3个运动周期内齿轮副由进入啮合到退出啮合的循环次数约为4次。 由于不同试验对应的泄漏流量以及含气油液的压缩流量有所不同,因此出口瞬时流量曲线出现很大差异。进一步,分别获取图3中瞬时流量对应脉动幅值Δq及相应脉动率δq的柱状图,如图6所示。 图6 不同试验条件对应的流量脉动幅值及脉动率 在图6中,流量脉动幅值及对应脉动率整体偏大,尤其是脉动率,需要说明的是,由于严重的内泄漏,试验3的瞬时流量出现了负值,其对应的脉动率及脉动幅值在此不作比较。为进一步分析因子对流量脉动率的影响程度,同时根据平均脉动率的高低来确定最优水平组合,分别获取不同试验对应的流量脉动率正交试验分析表,如表7所示。 表7 流量脉动率正交试验分析表 由极差法可知,表7中影响瞬时流量脉动率的各因子主次关系为:B>A>C,即工作压力是最主要因子,其次为含气量,最后为工作温度。随着工作压力的增加,流量脉动率显著增大。原因是出口压力越大,不均匀的内泄漏越多,对应的流量脉动率越高。 随着含气量的增加,流量脉动率不断增大。原因是油液等效体积弹性模量随含气量的增加显著减低,油液的压缩性明显增大,从而加剧了流量脉动率。然而,工作温度对流量脉动率的影响没有表现出明显的正相关或者负相关,整体上工作温度较高,流量脉动率较大,工作温度为40 ℃时流量脉动率最小。 进一步,表7反映出流量脉动率最低的水平组合为A1B1C1,即含气量为0.1%,工作压力为7.5 MPa,工作温度为40 ℃。经验证,此组合下齿轮泵的出口流量脉动率为13.55%。 流量脉动遇到系统回路阻抗时会激发出压力脉动。脉动的压力不仅损坏系统内薄弱的零部件,还会引起元件振动同时产生流体噪声等,是一种有害的现象。分别获取不同试验对应的出口瞬时压力psh曲线,如图7所示。 由图7可知,类似瞬时流量曲线,在0~0.01005 s的时间内不同试验对应的出口瞬时压力曲线也是脉动的,且全部呈现连续周期性变化,同时有约4个起伏脉动。 进一步,分别获取图7中瞬时压力对应脉动幅值Δp及相应脉动率δp的柱状图,如图8所示。 图7 不同试验条件下出口瞬时压力曲线对比 由图8可知,瞬时压力对应的脉动幅值及相应脉动率整体都很低,试验3的压力脉动幅值最高,最大值低于22 kPa;试验7的压力脉动率最高,最大值低于0.18%,该值与流量脉动率相比,可忽略不计。 图8 不同试验对应的压力脉动幅值及脉动率 为进一步分析试验因子对压力脉动率的影响程度,同时根据平均脉动率的高低确定最优水平组合,分别获取不同试验对应的出口压力脉动率正交试验分析表,如表8所示。 表8 压力脉动率正交试验分析表 由极差法可知,表8中影响瞬时压力脉动率的各因子主次关系为:C>A>B,即工作温度是最大因子,其次为含气量及工作压力。由于各因子对应水平的任意组合对压力脉动率的影响完全可忽略,此处不再进行分析。 齿轮泵中高压油在剪切力及液压力的双重作用下不可避免地流入低压腔,从而造成泄漏流量损失;另外,由于含气油液的压缩性较大,在高压作用下产生不同程度的压缩流量损失。这两个原因是导致容积效率降低的主要因素。 齿轮泵运行时,转子区域流体质点的运动方向非常紊乱,不同流层之间的油液相互碰撞、摩擦,损耗掉原有的动能,造成摩擦损失;另外,油液流动过程中还产生大小各异的漩涡,这些漩涡从主流获得能量,最后在黏性作用下转化为热能,导致黏性损失;还有其他因素导致齿轮泵出现机械损失,此处不再说明。以上原因导致工作过程中齿轮泵总效率会出现下降,分别获取不同试验对应的瞬时输入功率曲线,如图9所示。 图9 不同试验条件下瞬时输入功率曲线对比 由图9可知,与瞬时流量及压力曲线一样,瞬时输入功率曲线在0~0.01005 s的时间内也是脉动的且全部呈现连续周期性变化,同时有约4个起伏脉动。 经对比发现,出口初始压力与对应瞬时输入功率正相关。相同出口初始压力下,试验4、试验5及试验3瞬时功率对应的波峰值最大;同时,试验4、试验2及试验3对应的波谷值最小。进一步,分别获取图9中瞬时输入功率对应容积效率ηv及相应总效率ηt的柱状图,如图10所示。 在图10中,除试验1之外,其余试验对应的容积效率及总效率整体偏小,尤其是总效率。容积效率变化趋势和总效率非常接近,容积效率正相关于总效率。 图10 不同试验对应的容积效率及总效率 为进一步分析试验因子对容积效率及总效率的影响程度,同时根据平均容积效率及总效率的高低来确定最优水平组合,分别获取不同试验对应的容积效率及总效率正交试验分析表,如表9、表10所示。 表9 容积效率正交试验分析表 由极差法可知,表9中影响容积效率的各因子主次关系为:B>C>A,即工作压力是最大因子,其次为工作温度,含气量的影响可忽略。随着工作压力及工作温度地增加,容积效率显著降低。为了得到较高的容积效率,尽可能使齿轮泵工作在额定范围内。另外,要求系统中油温越低越好。进一步,表9反映出容积效率最高的水平组合为A3B1C1,即含气量为0.1%,工作压力为7.5 MPa,工作温度为40 ℃。经验证,此组合下齿轮泵的容积效率为98.12%。 由极差法可知,表10中影响总效率的各因子主次关系为:B>C>A,即工作压力是最大因子,其次为工作温度,含气量的影响可忽略。由于不同试验对应的机械损失基本相同,因此不同因子及对应组合对总效率的影响与容积效率一致,此处不再进行分析。另外,表10反映出总效率最高的水平组合为A3B1C1,即含气量为0.1%,工作压力为7.5 MPa,工作温度为40 ℃。经验证,此组合下总效率为84.68%。 表10 总效率正交试验分析表 (1)在0~0.01005 s的时间内不同试验对应的瞬时流量曲线、瞬时压力曲线以及瞬时输入功率曲线都是脉动的,且全部呈现连续周期性变化,同时有约4个起伏脉动,这与1/3个运动周期内齿轮副由进入啮合到退出啮合的循环次数完全吻合; (2)工作压力分别是影响流量脉动率、容积效率及总效率的最主要因子,随着工作压力增大,流量脉动率显著增大,容积效率及总效率下降明显,各因子对应水平的任意组合对压力脉动率的影响完全可忽略不计; (3)不同试验对应的机械效率相差无几,容积效率正相关于总效率,同样是影响总效率的主要因素; (4)为了得到很低的流量脉动率、尽可能高的容积效率及总效率,应使用含气量非常低的油液,尽量使齿轮泵工作压力保持在额定范围内,同时不能长时间超额定值工作,另外,在合理的黏度范围内要求整个液压系统中的油温越低越好。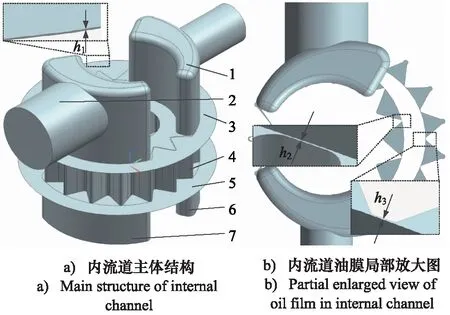
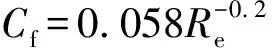
3.2 仿真参数设定
4 计算结果与分析
4.1 网格及收敛标准无关性验证
4.2 齿轮泵出口流量脉动分析
4.3 齿轮泵出口压力脉动分析

4.4 齿轮泵出口容积效率及总效率分析

5 结论

