基于改进分段截断二次速度轨迹模型的行程时间估计*

□ 陈诗意，潘义勇，魏双秋

(南京林业大学 汽车与交通工程学院，江苏 南京 210037)

行程时间是描述交通状态的重要指标，是出行者和交通管理者的决策依据[1-2]。由于城市交通环境下的出行极容易受到外部因素的影响，因此研究可靠的行程时间估计模型对交通管理和路径诱导有重要的意义[3-5]。目前行程时间的估计模型主要分为基于交通流理论的模型、基于数据的模型和混合模型三大类[6]。基于交通流理论的估计模型受限于参数和特定系数，可移植性较差。混合模型结合了历史和实时估计，虽然不需要进行参数估计，但历史和实时估计各自的重要度和影响程度却难以确定[7]。因此，更多行程时间估计的相关研究选择是基于数据的模型的。流量和占有率等交通流特征数据依赖于高精度的探测设备和识别系统，故目前基于数据的行程时间估计模型多采用速度数据来进行建模研究。

基于速度的行程时间估计模型一般利用速度-时间的关系构造模型。Li等[8]提出的瞬时速度模型和时间切片模型，分别考虑了速度在空间上的变化和速度在离散时间上的变化。Cortés等在瞬时速度模型的基础上提出了改进的动态时间切片模型，提高了模型估计的精度。但以上两种模型是以上下游路段节点同一时刻的速度平均值来计算行程时间的，没有考虑行程过程中速度随时间的变化，不符合现实中车辆在路段上速度变化的情况[9-10]。Van 等[11]提出的线性模型将上下游路段节点之间的速度表示为车辆所处位置的距离线性函数，虽然构造的速度轨迹平滑，但没有考虑速度在时间域的变化，而且实际中两个路段节点之间的速度并非随空间距离变化。为构造平滑连续的速度轨迹，有研究使用插值的方法基于断面速度数据对速度轨迹进行重构，如局部加权回归、三次样条插值和三次Hermite 插值法等[12]，但高次多项式插值近似速度轨迹的方法计算难度大，容易出现估计值震荡和难收敛。Sun等[13]提出的分段截断二次速度轨迹模型解决了上述高次多项式插值的问题，模型基于相邻的三个路段节点速度构造了拉格朗日二次插值速度轨迹，但相邻的三个路段节点速度采用出发时刻的速度，缺失考虑速度在时间域的变化，而且模型要求到达相邻路段节点的时刻间隔足够短，故无法应用在实际城市路段上。因此，速度轨迹重构模型有必要考虑速度在时间域和空间域的连续，从而构造近似真实的速度轨迹。

综上所述，现有的行程时间估计模型在构造速度轨迹上，仅考虑速度在空间上或在时间上的变化，使得速度轨迹不能在时间域和空间域连续，当道路处于拥塞状态时，估计的行程时间精度下降。本文在经典分段截断二次速度轨迹模型的基础上，考虑了速度在时间域的变化，提出了改进的分段截断二次速度轨迹模型。首先，根据行程经过节点上游路段的累计时间窗来计算节点到达速度。第二，用到达路段节点时刻的速度代替出发时刻的速度，根据相邻三个路段节点的速度构造速度轨迹。其次，基于估计的路段平均速度计算路径的行程时间。最后，针对实际路段开展实证研究，把改进模型的估计结果和原始模型进行对比，从而评估模型的估计性能，分析试验结果得出相关结论，为行程时间估计理论研究提供参考。

1 经典分段截断二次速度轨迹模型改进

1.1 经典分段截断二次速度轨迹模型

经典分段截断二次速度轨迹模型使用三个相邻的路段节点速度构造两段平滑的速度轨迹，如式(1)所示。模型考虑了车辆因不同的交通状态进行加减速的情况，以区间τ∈[AT2m-1(t),AT2m+1(t)]内历史速度的85%最大值、最小值作为常基函数限制，如式(3)-(4)所示。

v(τ)≈v(t,x2m-1)l2m-1(τ)+v(t,x2m)l2m(τ)+v(t,x2m+1)l2m+1(τ)

(1)

其中，l2m-1(τ)、l2m(τ)和l2m+1(τ)是拉格朗日二次基函数，分别为

(2)

考虑到不同交通状态下车辆的加减速情况，引入常基函数来构造边界速度。边界速度由历史数据中同一个时段的85%的最大速度vmax和最小速度vmin确定。在τ∈[AT2m-1(t),AT2m+1(t)]时，通过相邻的三个路段节点时间区间的速度与边界速度值的关系可以由式(3)和(4)表示：

v[AT2m-1(t),x2m-1]l2m-1(τ)+v[AT2m(t),x2m]l2m(τ)+v[AT2m+1(t),x2m+1]l2m+1(τ)-vmax=0

(3)

v[AT2m-1(t),x2m-1]l2m-1(τ)+v[AT2m(t),x2m]l2m(τ)+v[AT2m+1(t),x2m+1]l2m+1(τ)-vmin=0

(4)

式中，xm(m=0,1,2,...M)是路径上路段节点所在位置，M为奇数，ATm(t)(m=1,2,...,M)是车辆在t时刻出发后到达第m个路段节点的时刻；v[AT2m-1(t),x2m-1]、v[AT2m(t),x2m]和v[AT2m+1(t),x2m+1]分别是在第2m-1个、第2m个和第2m+1个这三个相邻路段节点处的速度；插值点τ∈[AT2m-1(t),AT2m+1(t)]。

1.2 模型改进

上述经典分段截断二次速度轨迹模型估计行程时间的隐含假设是交通流在时空间隔[AT1(t),ATM(t)]内是稳定流。为了使该假设成立，需要满足时空间隔[AT1(t),ATM(t)]足够短的前提，而且当路段处于拥塞的状态时将违反该假设。由于实际中路段节点的间隔有一定距离，所以在t时刻第m个路段节点处测得的速度，不一定等于t时刻出发的车辆的速度，故构造的速度轨迹难以近似真实的车速轨迹。

在原模型基础上，根据原模型速度轨迹表达式存在的问题，用三个相邻路段节点到达时刻的速度v[AT2m-1(t),x2m-1]、v[AT2m(t),x2m]和v[AT2m(t),x2m]代替出发时刻测得的速度v(t,xm)、v(t,x2m)和v(t,x2m+1)，得到改进的分段截断二次速度轨迹模型，公式如(5)式所示：

v(τ)≈v[AT2m-1(t),x2m-1]l2m-1(τ)+v[AT2m(t),x2m]l2m(τ)+v[AT2m+1(t),x2m+1]l2m+1(τ)

(5)

式中，v[AT2m-1(t),x2m-1]、v[AT2m(t),x2m]和v[AT2m+1(t),x2m+1]分别是到达第2m-1个、第2m个和第2m+1个这三个相邻路段节点的速度，其他公式变量和参数的含义同传统的分段截断二次速度轨迹模型。

(6)

2 模型求解

本章对设计算法求解改进的分段截断二次速度轨迹模型。首先，对相邻三个路段节点时刻的时间间隔划分成n个微小的时间片段，第二，判断时间片位于对应节点的位置。其次，再根据拉格朗日二次插值基函数和常基函数用三个相邻节点的到达时刻速度构造速度轨迹。最后估计路段的行程时间，OD节点的总行程时间是各路段的行程时间之和。模型求解的步骤具体如下：

第一步：给定每个路段节点到达的时刻ATm(t)和其对应的速度v[ATm(t),xm]。

第二步：将通过路径节点时刻的总时间区间[AT1(t),ATM(t)]等分成n个时间间隔τ，τ=0∶n∶ATM(t)。

第三步：判断τ的位置，用三个相邻路段节点到达速度构造速度轨迹,计算插值τ处的函数值。

v(τ)≈v[AT2m-1(t),x2m-1]l2m-1(τ)+v[AT2m(t),x2m]l2m(τ)+v[AT2m+1(t),x2m+1]l2m+1(τ)

第四步：以历史速度85%最大值vmax和最小值vmin为常基函数，当速度超过该值时被代替。

ifv(τ)≤vmin

v(τ)=vmin

end

ifv(τ)≥vmax

v(τ)=vmax

end

第五步：行程时间估计。

3 实例应用

3.1 数据获取与预处理

为检验改进分段截断二次速度轨迹模型的拟合度，实验选取桂林市中山路北向南方向道路作为研究对象，全长5.2千米，双向六车道，设计车速为60km/h。获取数据的时间为2019年5月19日全天连续24小时，考虑到地图数据的更新速度，速度数据采样时间间隔为5分钟，路段的节点共17个。节点速度首先通过拾取两个临近节点的上下游位置坐标，以此获得较短的路段。其次，利用百度地图自带的DrivingRoute函数获得这个路段的驾车实例。最后将返回的微小路段的速度设为近似节点的速度。采用式(7)对原始速度数据进行异常值判断和平滑处理，当实际值与移动平均后的值偏差大于50%时视为噪声，应该用移动平均后的值进行代替。对缺失数据采用插值法进行插补，如式(8)所示。

(7)

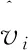
(8)

式中，t是缺失数据值对应的时刻，v(t0)是缺失数据的前一个数据，v(t1)是缺失数据的后一个数据，t0是缺失数据的前一个数据所对应的时刻，t1是缺失数据的后一个数据所对应的时刻。

3.2 误差分析

为量化模型的拟合度，采用均方根误差(RMSE)和平均绝对百分比误差(MAPE)作为评价指标。改进的分段截断二次速度轨迹模型和原模型的行程时间估计值与真实值的相对误差结果对比如图1所示，模型对应的综合评价指标的对比如表1所示。在估计路径总行程时间时，原模型的相对误差基本保持在±15%之间，改进的分段截断二次速度轨迹模型的相对误差更低，基本能保持在±10%之间。改进的分段截断二次速度轨迹模型的均方误差和平均绝对百分比误差比原始模型分别降低了46%和51%。

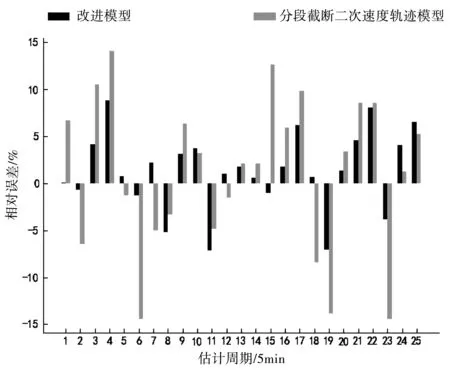
图1 模型的相对误差对比

表1 模型估计误差指标比较

3.3 结果分析

①如图2所示，当处于8∶00-9∶00时段(出行的高峰时段)时，研究道路的行程时间受交通状态的影响而波动。改进的分段截断二次速度轨迹模型估计的行程时间与原模型相比能更好地拟合真实行程时间，说明用节点到达时刻速度构造速度轨迹突破了原模型的局限性，能适应拥堵条件下的行程时间估计。

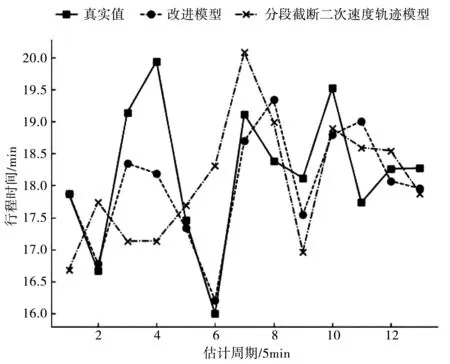
图2 8∶00-9∶00模型结果对比

②如图3所示，当处于非出行高峰时段(9∶05-10∶00)，原模型比改进的分段截断二次速度轨迹模型更容易出现高估的情况，改进的分段截断二次速度轨迹模型与真实数据比较表现出良好的一致性。

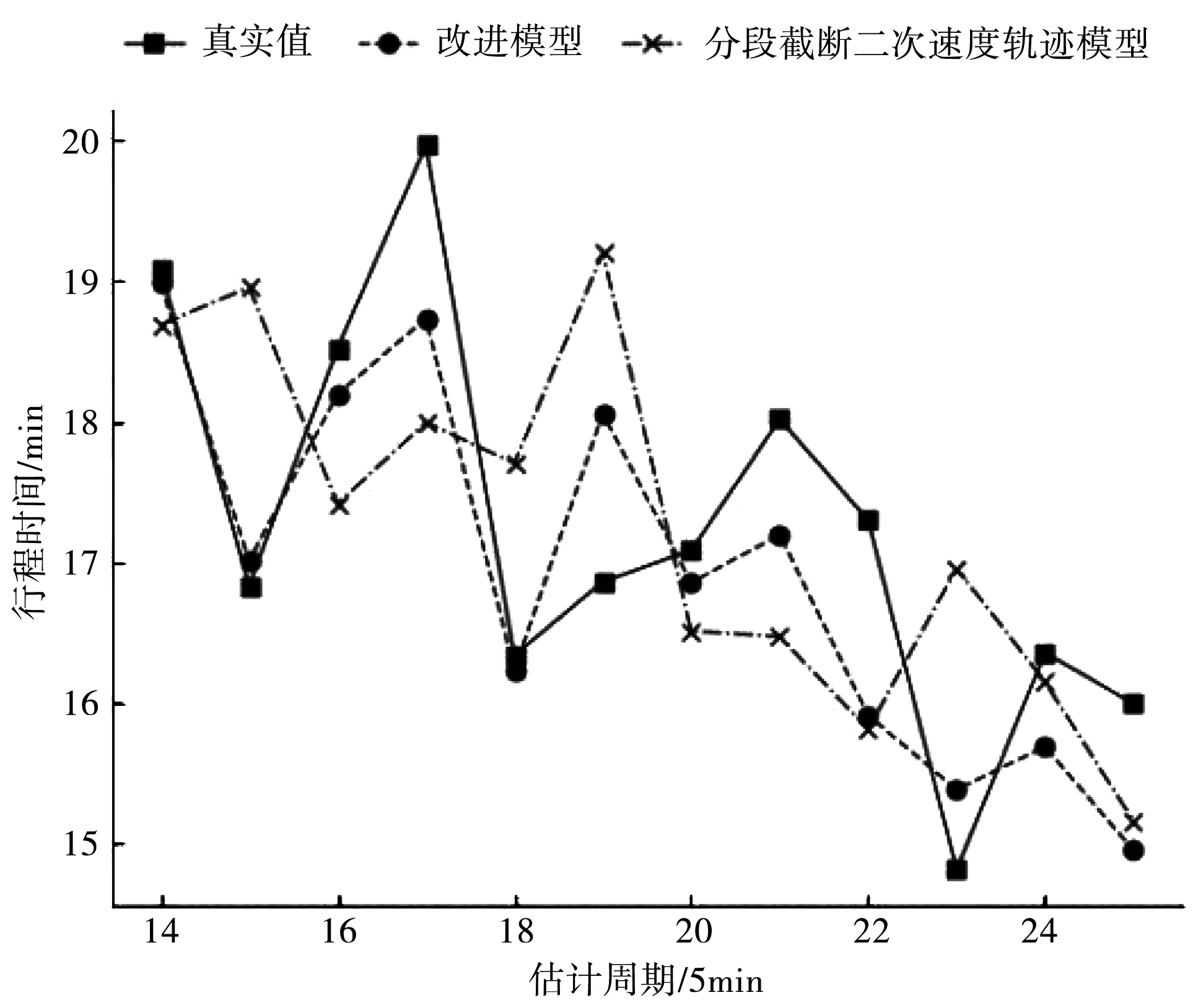
图3 9∶05-10∶00模型结果对比

综上所述，改进的分段截断二次速度轨迹模型估计结果与真实行程时间拟合较好，且估计结果与真实行程时间随时间的变化趋势一致。改进的分段截断二次速度轨迹模型对交通状态的变化反应更灵敏。说明改进的估计模型能准确根据行程中的交通状态及时调整估计的行程时间，使其接近道路真实交通状况下的行程时间。

4 结论

本文在经典分段截断二次速度轨迹模型的基础上，考虑了行程中的速度变化，提出了一种改进的分段截断二次速度轨迹模型。首先，根据行程经过节点上游路段的累计时间窗来计算节点到达速度。其次，用到达路段节点时刻的速度代替出发时刻的速度，并用相邻的三个路段节点的到达速度构造速度轨迹，引入常基函数构造边界速度作为限制。最后，基于路段的平均速度估计行程时间。针对实际道路开展实证研究，试验结果表明：(1)改进的分段截断二次速度轨迹模型比原模型在均方误差和平均绝对百分比误差上分别降低了46%和51%。(2)当处于出行高峰时期，改进的分段截断二次速度轨迹模型与原始模型相比提高了拟合度。证明了改进后的模型能适应拥堵的交通状态，突破了原始模型的局限性。(3)改进的分段截断二次速度轨迹模型对原模型高估或低估的问题有显著的改进，对交通状态变化的反应更灵敏。

本文用改进的分段截断二次速度轨迹模型估计行程时间，模型不涉及利用历史数据进行短时的预测。如何利用历史和当前的节点速度实现行程时间的实时估计，在后续研究中需要进一步完善。