曲线区段受电弓-接触网系统建模及动态性能分析

熊嘉铭，徐 钊，鲁小兵，刘志刚，宋 洋

(1.西南交通大学 国家轨道交通电气化与自动化工程技术研究中心，四川 成都 610031；2.中铁二院工程集团有限责任公司，四川 成都 610031；3.挪威科技大学 结构工程系，特隆赫姆 7491)

高速铁路列车通过受电弓与接触线之间的滑动接触将电能从接触网传输到机车。弓网间的动态性能不但直接决定受流质量，同时也影响弓网系统各部件的服役寿命和电气化铁路的安全可靠运行。随着高速铁路的不断提速与运营里程的不断增加，弓网动态性能的评估与优化受到越来越多研究者的关注。

接触网建模通常采用非线性有限元方法[1-2]。其中，接触线、承力索等线索可以等效为梁单元[3-4]或索单元[5]，定位器、线夹、腕臂、吊弦等部件则可通过与频率相关的有限元法等效为单独的质量块或振动单元[6]。为保证施加了线索张力与结构自重的接触网静态位移符合规范，还需确定接触网的初始平衡状态[7-9]，常用方法有基于有限单元的分模法[10]、绝对节点坐标法(ANCF)[11-12]与负弛度法[13]。受电弓模型主要有两类：归算质量模型与多体模型。归算质量模型的各项参数可通过频率响应法计算得到[14-15]，通过该方法建立的受电弓模型可以保证在0～20 Hz频率段的有效性[15]和0～350 Hz频率段频响特性的精确性[14]。受电弓多体模型可基于相对坐标系下的R/W方程建立，通常应用于受电弓的优化设计研究[16]。

评估弓网动态性能与受流质量的优劣，通常关注的指标包括弓网接触压力、导线动态高度及燃弧等[17]。其中接触压力作为重点研究对象，可通过建立弓网耦合动力学模型获取[18-20]。分析接触力在时域上的各项统计指标从而获得接触力的波动特性，是评价弓网动态性能的有效方法。接触力产生波动内部因素主要有接触线振动波传播[21]和接触线不平顺[22]；外部激励主要有风载荷[23-26]、空气动力不稳定性[27]、机车激励[28]和温度变化[29]等。此外，采用频域分析法对接触线谱进行研究，计算接触线不平顺的波长成分及各波长的不平顺幅值，以获取弓网动态性能的频域特性[30-32]。

现阶段有关弓网动态性能的研究往往基于直线区段展开，对曲线区段弓网动态性能的研究较少。文献[33]建立曲线区段简单链型接触网有限元模型与受电弓多体模型，通过车顶轨迹确定受电弓的位移，采用联合仿真研究弓网系统的耦合动力学行为，证明曲线区段与直线区段的弓网动态性能存在差异。文献[34-35]通过研究曲线区段线路参数、列车振动、施工维修误差与接触线风偏移等因素，给出不同曲率半径线路下的拉出值设置范围。然而，曲线区段接触网导高以轨面坐标系定义，轨面的倾斜导致了接触网在世界坐标系下并非垂直架设，其各组成部件的空间几何位置均会发生改变。同时受电弓随列车的侧滚运动而倾斜，运动状态从平直运行变成曲线倾斜运行，滑板、上框架与下框架的空间几何位置也发生相应的改变。其中接触网空间位置与受电弓运行状态的改变还将导致受电弓与接触线的耦合接触方向从世界坐标系下的垂向方向转化为倾斜轨面的垂向方向，这些变化必然会对弓网动态性能产生多方面的影响。

基于曲线区段弓网系统空间几何位置与受电弓运行状态的特殊性，本文对接触网与受电弓的曲线特性进行数学解析。采用中国西南地区某高速铁路客运专线弹性链形接触网的设计参数与线路参数，建立接触网与受电弓在曲线区段的动力学耦合模型。通过对受电弓简化方案的可行性分析，证明弓网模型考虑曲线特性的必要性。基于所建模型，对不同曲率半径、不同拉出值设置方式以及直、曲线线路下的弓网动态性能进行分析。

1 曲线区段弓网建模

本章主要介绍弓网系统有限元模型建立方法，以及曲线区段弓网系统的曲线特性及其数学解析过程，并采用EN 50318—2018[36]标准对接触网建模方法的准确性进行验证。

1.1 弓网建模及验证

利用有限元分析软件Ansys 建立弓网有限元模型。其中，接触网模型采用三维梁单元Beam188模拟接触线与承力索的空间非线性大变形，非线性弹簧单元Combin39模拟吊弦的抗拉特性，结构质量单元Mass21模拟线夹的集中质量特性。受电弓模型采用联合弹簧滑动器与阻尼器的Combin40单元建立。接触网结构约束包括：承力索座点处设置6自由度全约束；接触线端部定位点处设置3自由度位移约束，保证整体接触网结构的稳定；定位器底座处设置3自由度位移约束，保留腕臂的旋转能力。基于非线性有限元求解，计算弓网动态性能。构建的三维接触网模型如图1所示。

图1 三维接触网有限元模型

为证明本文建立的弓网模型的准确性，采用EN 50318—2018中接触网的静态标准与动态标准对模型进行验证。其中动态仿真选择0.25 m里程对应的采样步长与0～20 Hz接触压力滤波处理，并选取弓网接触力稳定后的接触力数据进行取值分析，以消除边界不稳定跨的边界效应影响。参考模型的结构与材料参数如图2与表1所示，此外接触网结构高度为1.8 m，吊弦间隔为9.17 m，吊弦数量为7个，跨距选取65 m，拉出值采用±300 mm，定位器长度为1.15 m。 表2为接触网的静态结果验证，其中接触线各点垂度误差低于标准规定误差(±5 mm)，恒定移动垂直力(200 N)下接触线等效弹性误差低于标准规定的误差(±0.1 mm/N)，静态结果满足EN 50318—2018标准规定。表3给出了接触网的动态结果验证，可以看出各项动态结果同样符合EN 50318—2018标准规定。由此认为本文使用的建模方法满足EN 50318—2018标准要求，可以进一步用于曲线区段弓网系统的动态性能分析。

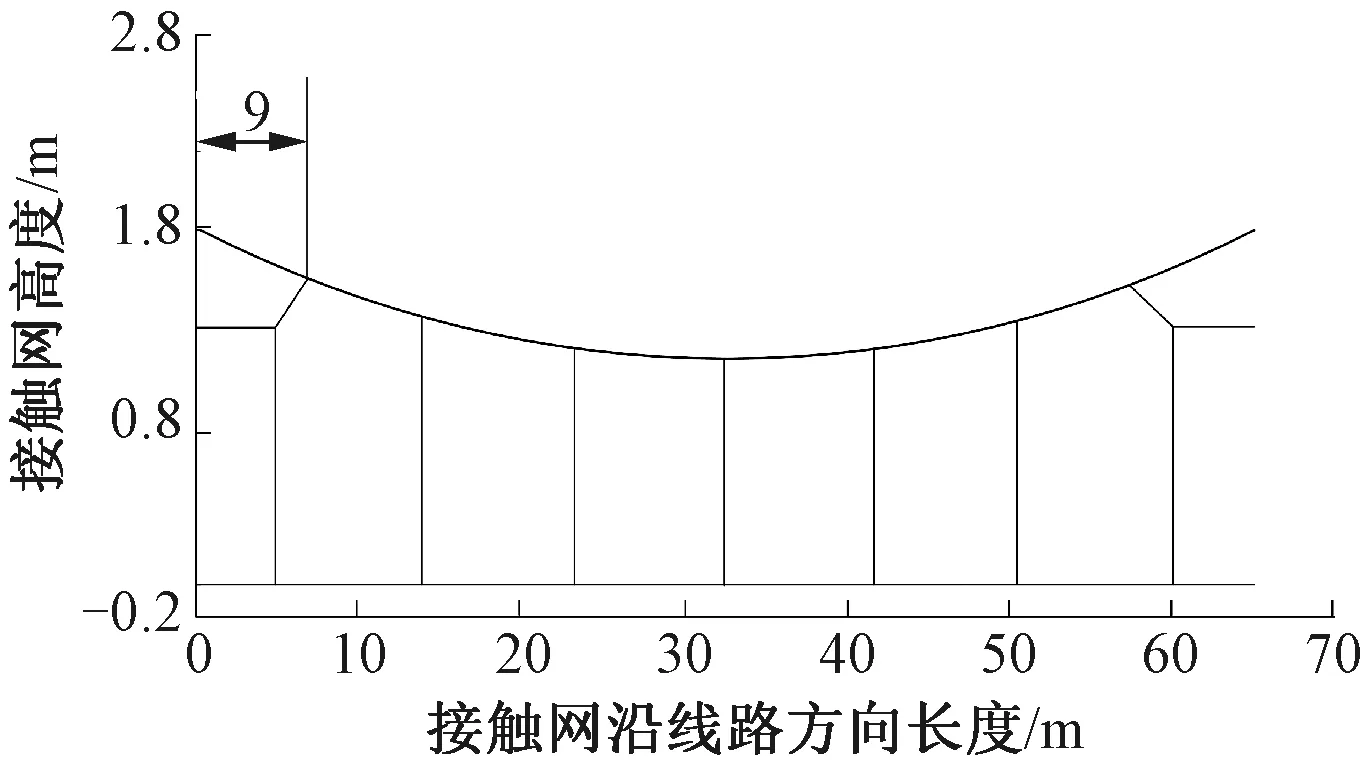
图2 弹性链型接触网结构示意

表1 接触网参考模型基本参数

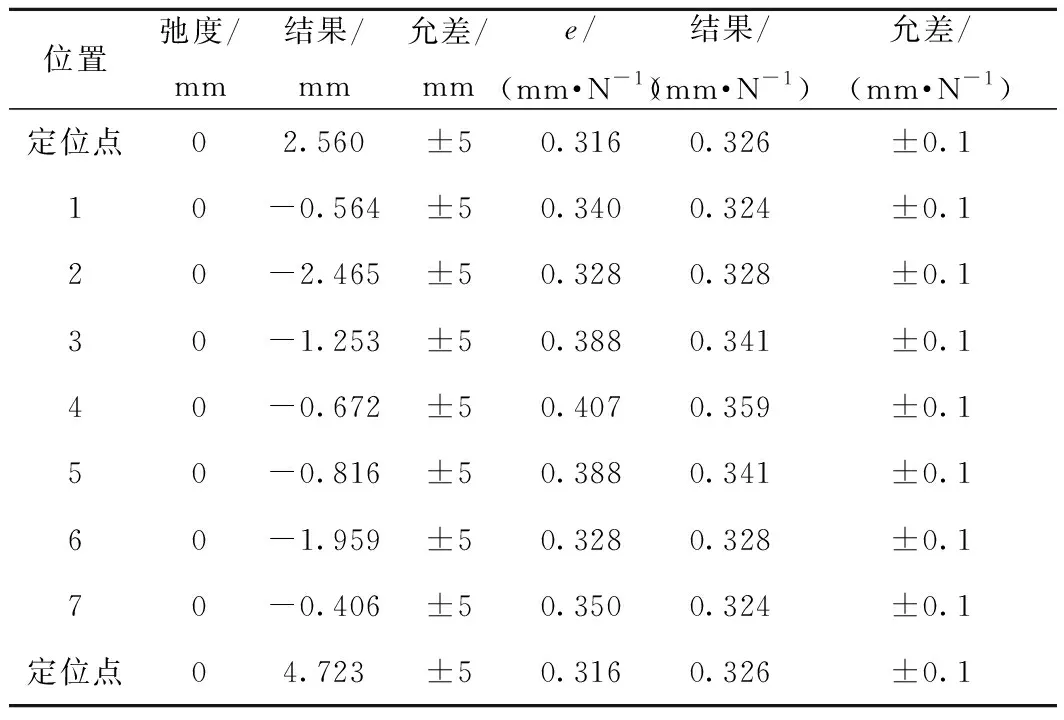
表2 静态结果验证

表3 动态结果验证

1.2 弓网曲线特性

为了使列车安全通过曲线区段，轨道外轨有一定程度的超高，利用车体自重产生的转矩来平衡所受到的离心力。外轨超高值的设置通常不超过125～150 mm，其导致的轨面倾斜即曲线区段弓网系统在动静态特性上均区别于直线段的根本原因。相比于直线区段，弓网系统在曲线区段由于轨面倾斜而产生的特殊接触网空间结构和受电弓运行状态，本文称之为弓网系统的曲线特性。

1.2.1 接触网曲线特性数学解析

接触网系统的曲线特性来自于确定接触网导高的轨面坐标系发生倾斜后，接触网在图3所示的世界坐标系下的空间几何位置产生了变化。值得注意的是，当相邻定位点处接触线的拉出值不相等时，为保证定位点至倾斜轨面的垂直距离为标准导高hcw不变，相邻定位点间势必会产生高度差，进而改变接触网的结构特征，如图4所示。

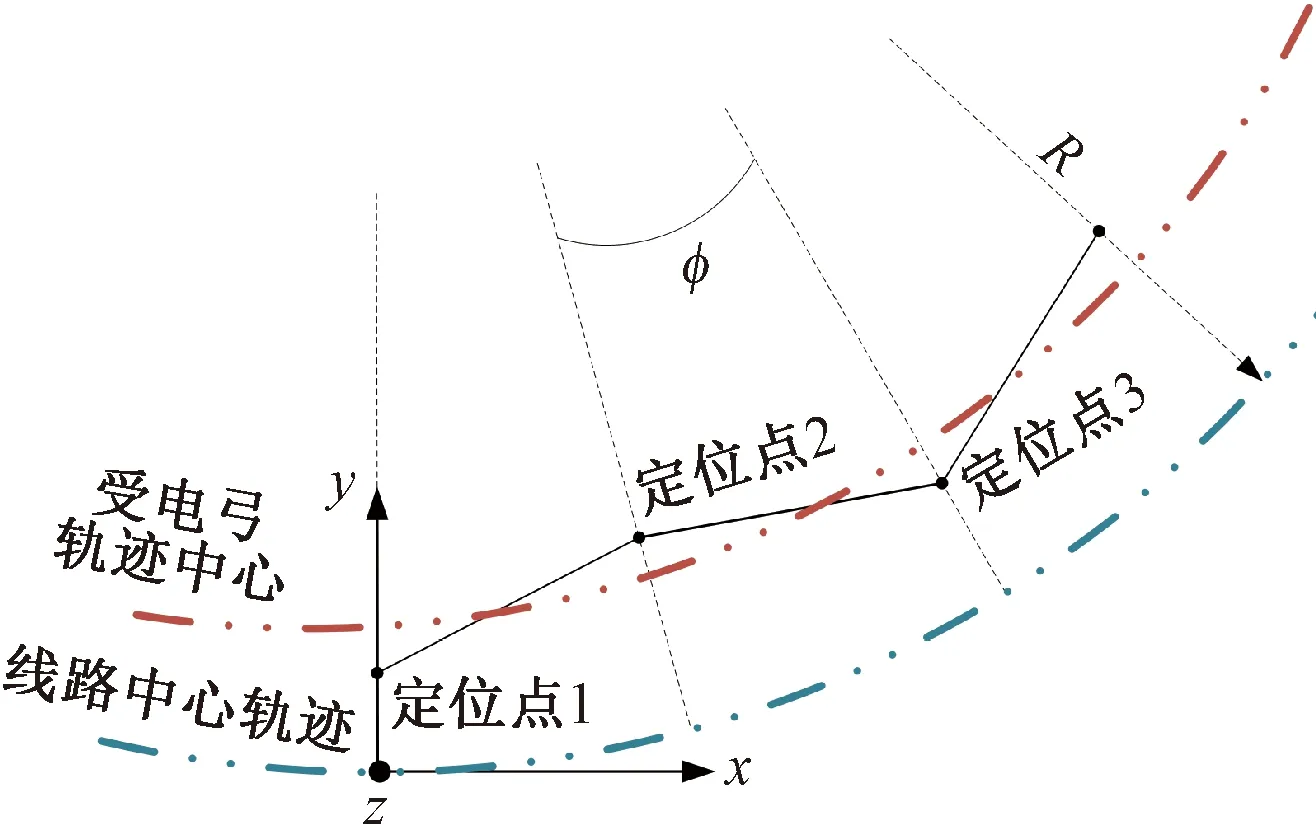
图3 接触网模型世界坐标系示意

图4 接触网模型曲线特性示意

在图3中定义世界坐标系坐标原点位于线路中心轨迹上，x轴沿线路切向方向，z轴沿线路法向方向，y轴沿地平面的垂直方向。线路中心轨迹方程可以表示为

x2+(z-R)2=R2

( 1 )

根据图4，将第i个定位点所对应的轨道中心坐标向量表示为

( 2 )

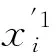
( 3 )

式中：R为线路的曲率半径；φ为当跨距为LA时对应弧长下的圆心角，可由余弦定理求得。

在考虑曲线特性对定位点空间位置的修正前，计算第i个定位点到对应线路中心之间的水平距离Li，用于辅助计算定位点的空间坐标。

Li=hcw×sinα-ai×cosα

( 4 )

式中：hcw为导高；ai为第i个定位点处设置的拉出值，取值如图4中相邻定位点拉出值a1或a2；Lc为标准轨距；α为轨道外轨超高导致的轨面倾斜角度，α=arcsin(h/Lc)。

( 5 )

( 6 )

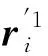
( 7 )

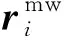
( 8 )

定位器与弹性吊索的空间位置可基于已确定的定位点和承力索座坐标递推获取。完成接触网曲线特性的数学解析后，构建曲线区段的三维接触网模型如图5所示。

图5 曲线区段接触网有限元模型

1.2.2 受电弓曲线特性数学解析

受电弓的曲线特性来自于轨道外轨超高导致的列车倾斜进而带动受电弓呈倾斜运行状态，如图6所示。此时受电弓中心相对线路中心产生了偏移，同时曲线区段受电弓整体也将保持一个固定的倾斜角度运行。对受电弓曲线特性的数学解析即确定受电弓中心的偏移量，得到计及该偏移量的静态受电弓弓头位置，完成受电弓初始位置的定位。受电弓的升弓过程与曲线倾斜运行过程可基于Ansys Apdl编程实现。

根据图6，将受电弓所在位置对应的轨道中心坐标表示为

( 9 )

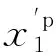
(10)

图6 受电弓模型曲线特性示意

(11)

式中：hp为静态受电弓滑板至轨面的垂直距离；se为受电弓弓头的工作长度。

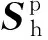
(12)

(13)

其中

(14)

(15)

得到受电弓滑板两端端点的空间坐标为

(16)

(17)

受电弓模型中其他关键点的空间位置均可采用同样方法求得。

2 算例的设置

采用第1章建模方法，建立曲线区段弹性链型接触网和三元归算质量受电弓模型，并设置多组算例研究曲线区段弓网系统动态特性，算例中弓网模型的基本参数见表4，此外接触网结构高度为1.8 m，吊弦间隔为9.17 m，吊弦数量为7个，跨距选取65 m，拉出值采用±300 mm，定位器长度为1.15 m。算例间的差异性参数见表5。受电弓、接触网和轨道参数均来自中国西南地区某高速铁路客运专线，不同曲率半径线路下接触线的拉出值设置参考文献[33-35]。

表4 弓网模型基本参数

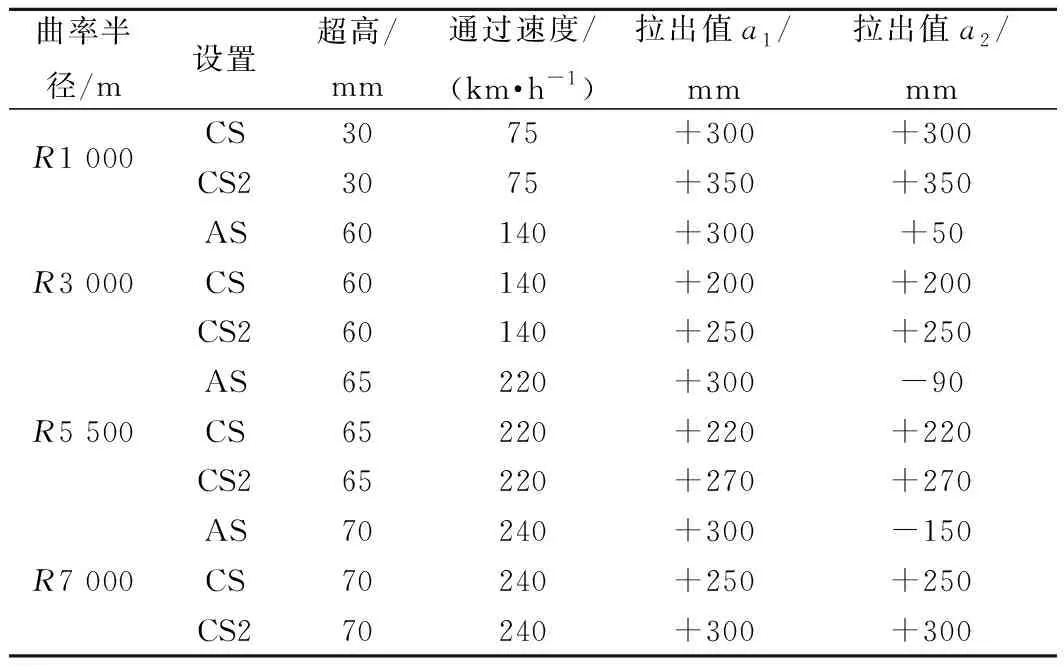
表5 算例设置

3 曲线区段受电弓建模

如图7所示，直线区段的受电弓呈平直状态运行，而曲线区段的受电弓呈倾斜曲线运行状态。考虑接触线建模采用圆截面的Timoshenko梁单元，且受电弓模型对位移与力的响应始终沿滑板的法向方向，故两种受电弓运行状态只改变了受电弓滑板与接触线之间的接触方向，弓网耦合接触行为的本质并没有发生改变。基于Ansys仿真分析，相比于倾斜曲线运行状态，直线状态的受电弓模型在仿真中需要更少的节点自由度约束与位移约束。采用平直状态的受电弓模型进行曲线区段弓网仿真的方案，可以降低计算难度与时间。本章验证该方案是否能保证仿真结果的准确性。

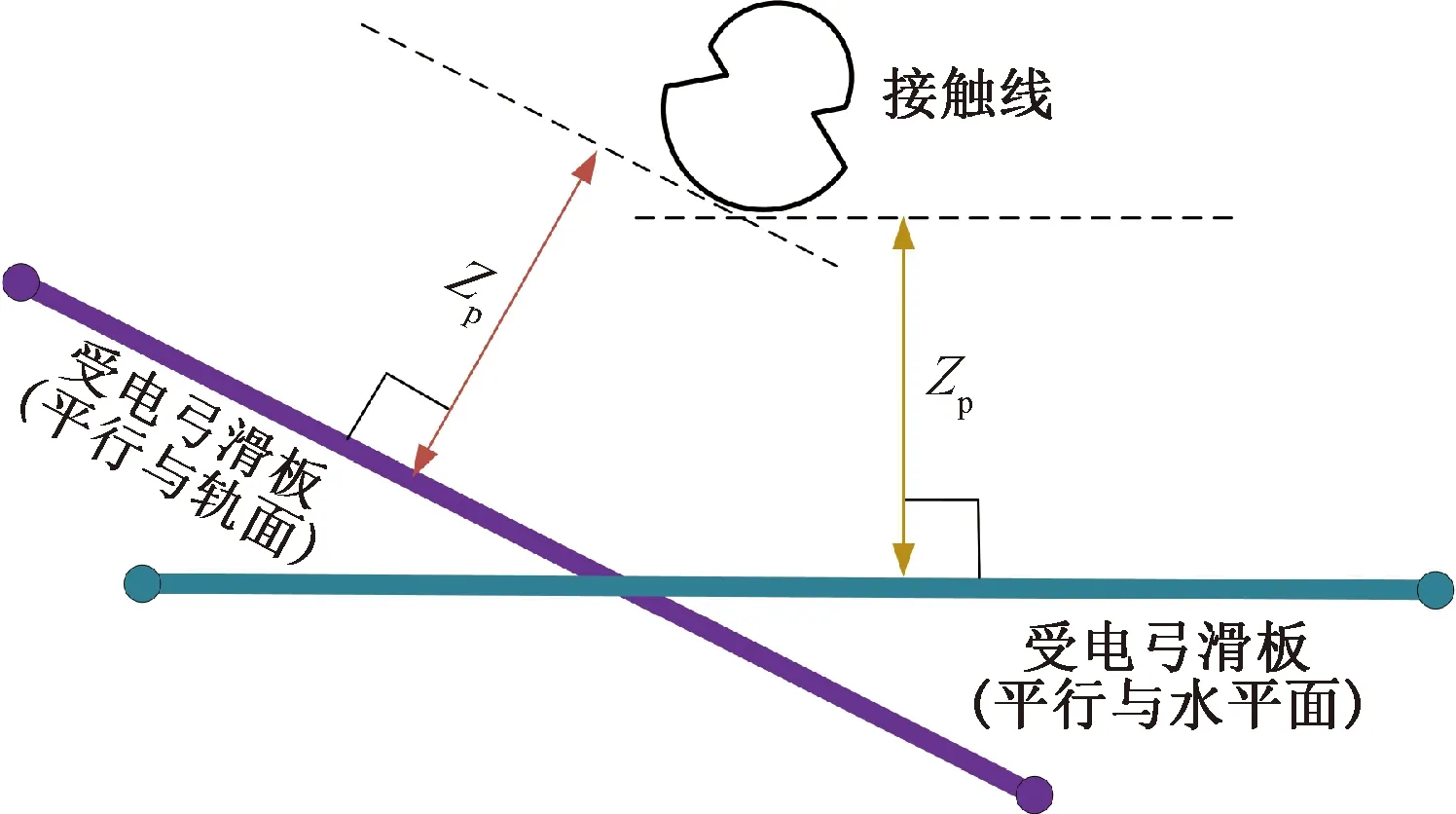
图7 弓网接触示意

采用R3 000-AS、R5 000-AS和R7 000-AS三组算例，分别设置两组受电弓模型，一组模型考虑曲线特性，另一组模型忽略曲线特性。如图8所示，选取弓网接触力稳定后的四跨接触力数据进行取值分析，结果见表6。分析表6结果可知，采用忽略曲线特性的受电弓模型对弓网接触力的平均值没有产生显著的影响，但明显增大了接触力的标准差，在R3 000、R5 500和R7000三组算例下接触力标准差分别增加了9.02%、6.7%和7.0%，导致接触力的波动变得更剧烈。

图8 接触力分析取值区段

对该现象产生的原因进行分析，通过图7可知，在曲线区段，受电弓局部坐标系下的接触线垂向静态位移并非传统世界坐标系下的垂向静态位移，而是世界坐标系下的接触线垂向静态位移向弓网接触方向转化

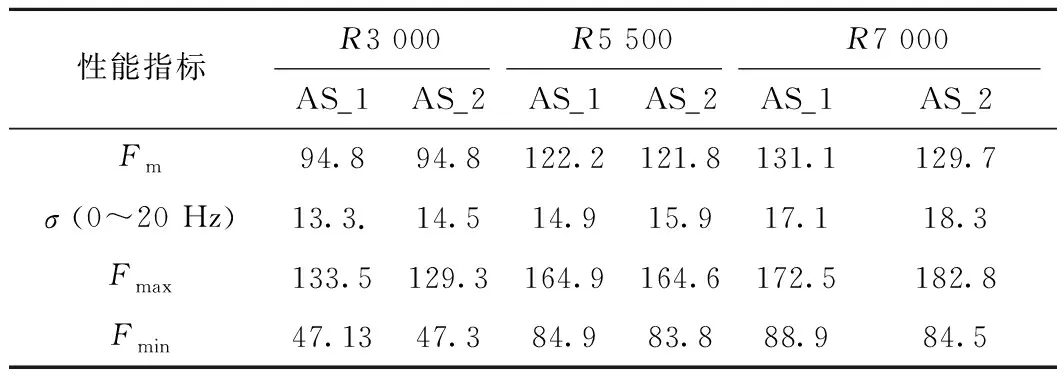
表6 不同受电弓模型下的动态性能指标 N

后的结果。为分析受电弓在实际运行过程中受到的来自接触线垂向静态位移的影响，定义受电弓局部坐标系下接触线垂向静态位移为Zp，为计算方便，取在定位点处Zp的初始值为0 m时受电弓滑板运动轨迹面作为基准，Zp即为线路上受电弓滑板到接触线的实际静态距离。三组算例中接触线的两跨Zp曲线如图9所示。

图9 不同受电弓模型下Zp曲线对比

由图9可知，当受电弓模型忽略曲线特性时，其Zp曲线的波动更加剧烈，且波动周期也从单跨长度50 m增加到双跨长度100 m。

结合接触网结构特性，由于相邻定位点之间的高度差值远大于接触线垂向静态位移，此时Zp被定位点高度差主导，从而导致动态性能的恶化。以曲率半径为3 000 m的算例为例，对Zp曲线和弓网接触力进行频谱分析，如图10所示。当受电弓模型考虑曲线特性时，Zp成分与接触力成分在低频段具有良好的对应关系，与文献[37]所得结论一致，且Zp成分的最大峰值对应频率为0.76 Hz，对应波长51.11 m，约等于实际跨距50 m。而当受电弓忽略曲线特性时，Zp成分的最大峰值对应频率为0.38 Hz，对应波长102.48 m，约等于实际跨距的两倍(即定位点高度变化周期100 m)，且此时Zp成分与接触力成分并未保持对应关系，同样的分析结果也出现在R5 000-AS和R7 000-AS两组算例上。结果表明忽略曲线特性的受电弓建模方法会导致Zp值被相邻定位点的高度差主导，弓网静态距离对接触力的影响被屏蔽，为保证仿真结果的准确性，该方案不可取，同时也证明了曲线区段弓网模型考虑曲线特性的必要性。

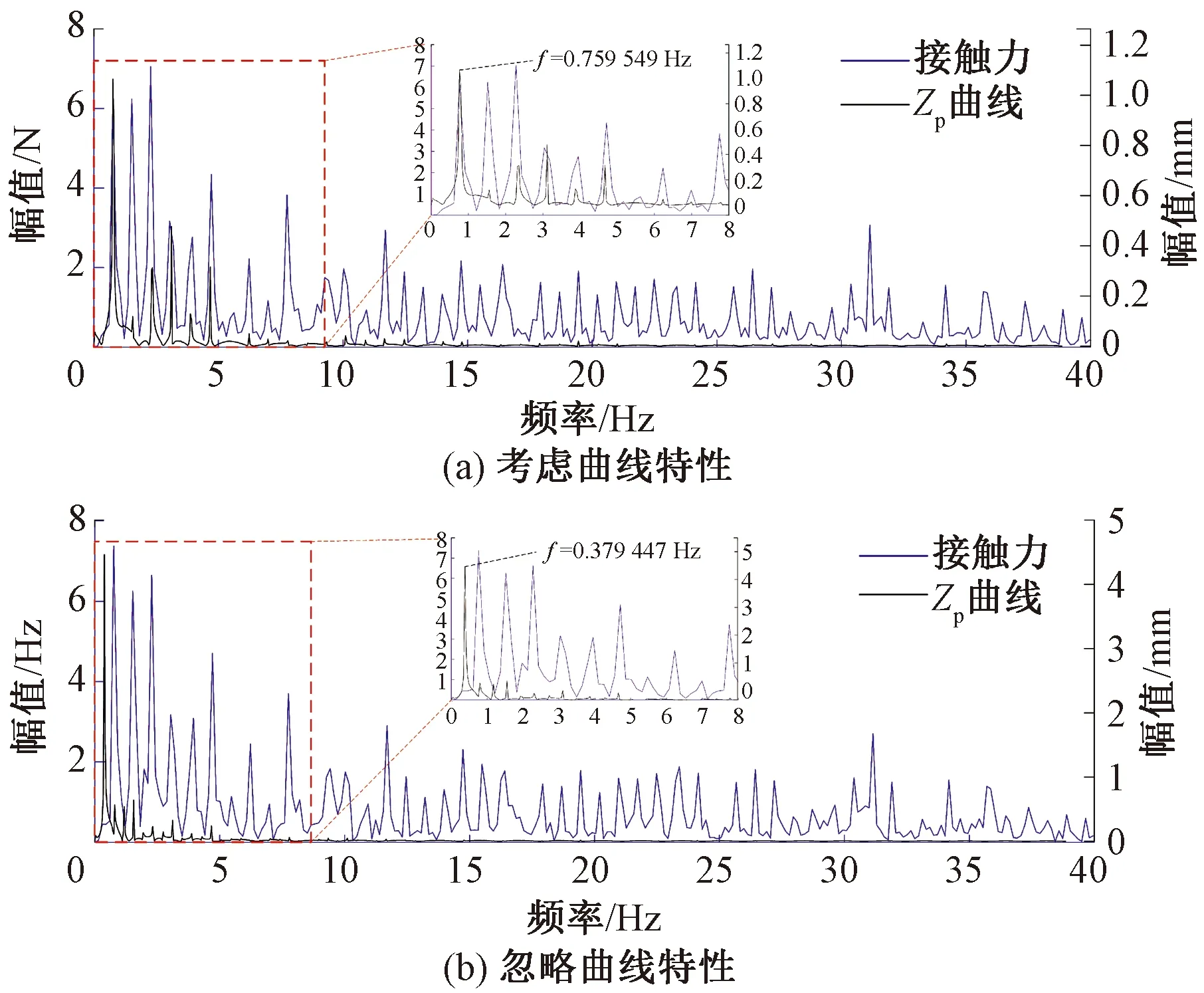
图10 R3 000m线路不同受电弓模型动态仿真的弓网接触力与Zp频谱分析

4 曲线区段弓网动态性能

采用计及曲线特性的弓网模型，分析曲线区段拉出值设置和直、曲线路对弓网动态性能的影响。

4.1 拉出值设置对弓网动态性能影响

曲线区段拉出值的设置不仅影响定位点的空间位置坐标，还会对接触网结构产生影响。当拉出值a1与a2相等时，相邻定位点在竖直方向上等高；当拉出值a1与a2不等时，相邻定位点存在高度差。实际接触网设计与应用中，定位器通常在小曲率半径线路上采用单向安装而在大曲率半径线路上采用正反交错安装，但为全面对拉出值设置方式对弓网动态性能的影响进行研究，因此对每组算例均设置两种安装方式。

对表5所列算例结果进行分析，接触压力标准差如图11所示。由图11可知，拉出值的设置方式影响弓网动态性能，当拉出值恒定设置时，弓网接触力标准差更小；拉出值恒定设置后，改变该定值的大小不会对接触力标准差产生影响。

图11 不同拉出值设置下接触力标准差对比

拉出值的设置同时也对受电弓滑板上接触点的运动范围产生影响。过小的接触点运动范围会引起受电弓的偏磨现象，而过大的接触点运动范围则会引起受电弓的刮弓现象。因此在分析曲线区段拉出值设置对弓网动态性能影响的同时，应兼顾拉出值设置对接触点运动范围的影响，保证在允许的接触点运动范围内使受电弓滑板的磨耗更加均匀。受电弓滑板的磨耗区域如图12所示，其磨耗区间的大小取决于定位点处或跨中处的接触线空间位置。各算例中滑板磨耗区间见表7。

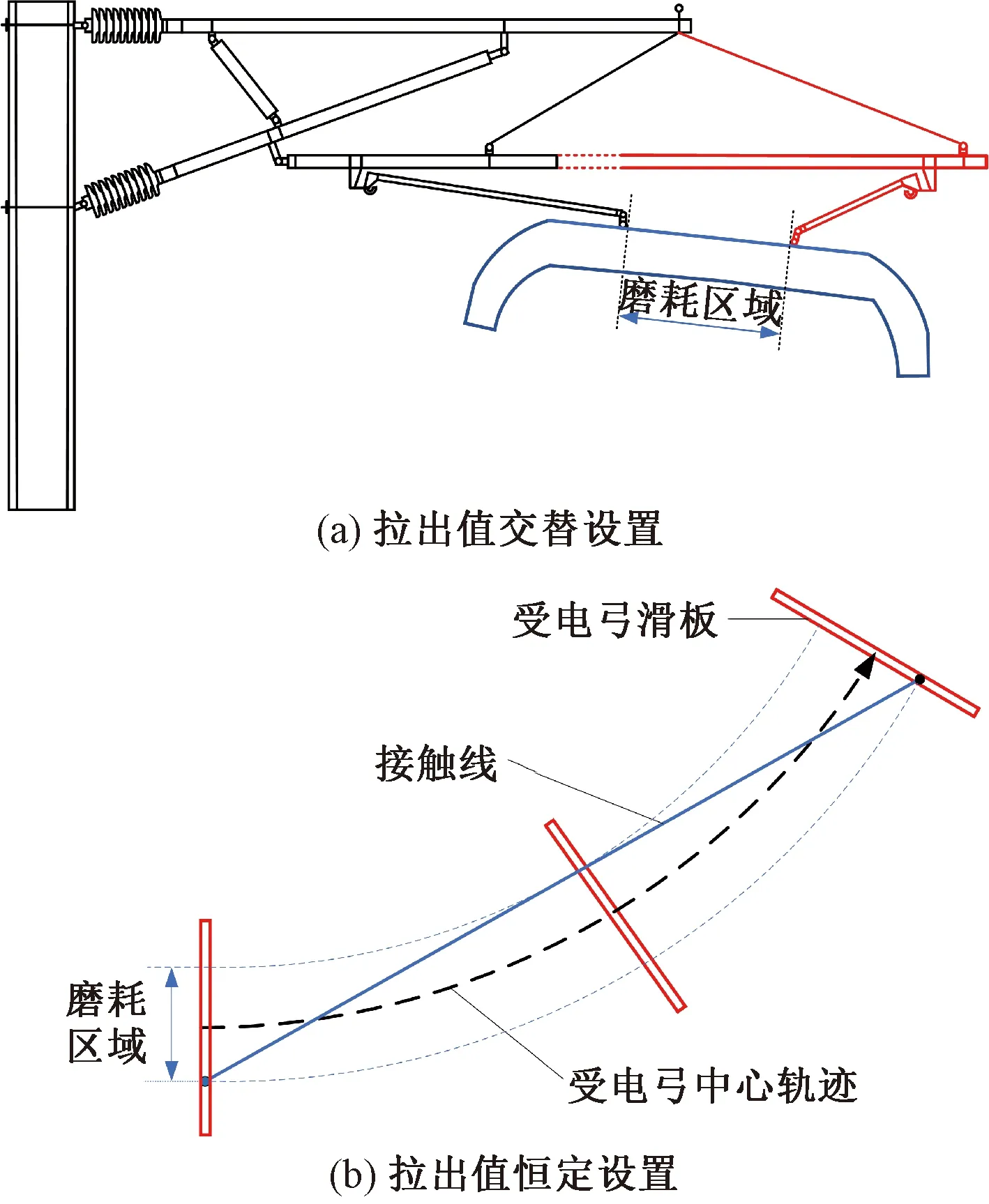
图12 受电弓滑板磨耗区域示意图

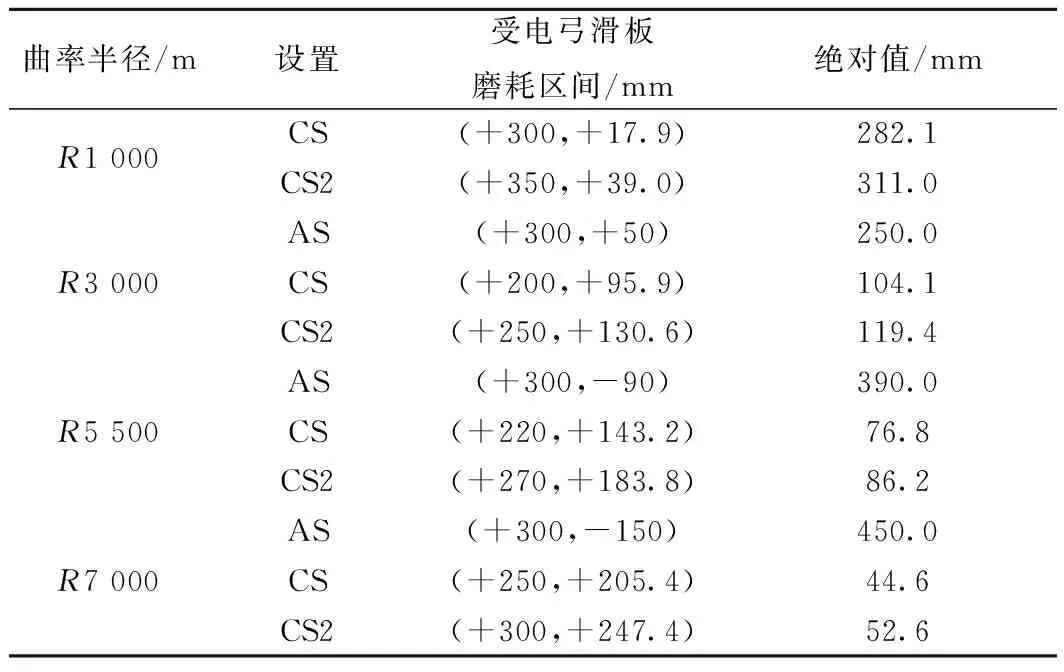
表7 不同拉出值设置下滑板磨耗区域对比

由上述可知：

(1)由于线路轨迹为曲线，即使将拉出值设置成定值，受电弓滑板上的接触点仍存在往复运动范围。

(2)拉出值恒定设置下的滑板磨耗区间更小，导致受电弓滑板的局部磨耗更严重，降低其服役寿命。

综上所述，在曲线区段设计接触线拉出值时，较好弓网动态性能与较大受电弓滑板磨耗区间不能同时兼顾，应根据首要设计需求与实际情况综合考虑。

4.2 直、曲线区段弓网动态性能对比

建立直线区段弓网模型，采用与曲线区段弓网模型相同的材料参数，并在该模型下使受电弓分别以各曲率半径线路的允许通过最大速度运行，进行直、曲线区段弓网动态性能的对比研究。由图13可知，相同条件下曲线区段的弓网接触力标准差更大，其中曲率半径最小的R1 000-CS算例的接触力标准差相比直线算例增加了19.3%，曲率半径最大的R7 000-AS和R7 000-CS算例的接触力标准差相比直线算例分别增加了18.4%和16.6%，证明基于直线区段的弓网动态性能测试并不能保证曲线区段弓网动态性能也满足标准要求。

图13 直、曲线路接触力标准差对比

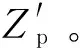
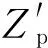
(2)曲线区段Zp曲线的波动远大于直线区段的Zp曲线，即接触线在受电弓局部坐标系下的垂向静态位移大于其在世界坐标系下的垂向静态位移，导致接触力波动更加剧烈。

图14 直、曲线区段曲线对比

4.3 曲线区段弓网接触力频谱分析

引起接触力波动的原因主要有4类：

(1)接触网刚度分布引起的接触力波动。

(2)外部环境对弓网的激励，如环境风和覆冰等。

(3)接触线由于长期使用过程中的机械磨损和维护过程的不规范导致的表面不平顺现象。

(4)接触线上振动波的传递。

弓网动态性能恶化的主要原因为第一类，在基于直线区段弓网接触力的频谱分析中，大多接触力成分直接来自于接触网周期性结构参数，但基于曲线区段的接触力分量在低频段与高频段的分布仍然值得探讨。本节针对3个算例进行曲线区段弓网接触力的频域特性分析。

(1)R1 000-CS

本算例中列车以75 km/h的速度在曲率半径为1 000 m的线路轨道上运行，接触力频谱分析如图15(a)所示。图中，SPF表示跨距通过频率，HSPF表示半跨距通过频率，ZpPF表示Zp曲线通过频率，SDPF表示定位点到吊弦通过频率，DDPF表示吊弦到吊弦通过频率，可以看出接触力的低频成分占主导地位，其中在频率0.41 Hz处为最大峰值，对应波长为51.2 m，约等于实际跨距50 m。对主要峰值进行比较，除频率为1.22 Hz处的接触力成分是由Zp分量引起的，其他幅值较大的接触力成分均可以找到对应的接触网周期性结构。

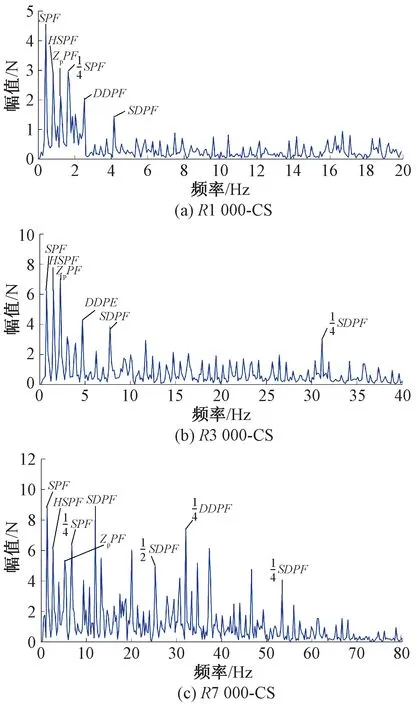
图15 接触力成分频域分析

(2)R3 000-AS

本算例中列车以140 km/h速度在曲率半径为3 000 m的线路轨道上运行，接触力频谱分析如图15(b)所示。可以看出接触力的低频成分仍占据较大的比重，但在频率为31.14 Hz处出现了一个可明显辨识的分量，对应波长为1.25 m，等于四分之一定位点到吊弦的距离1.25 m。

(3)R7 000-AS

本算例中列车以240 km/h的速度在曲率半径为7 000 m的线路轨道上运行，接触力频谱分析如图15(c)所示。随着速度的进一步提高，可以看到接触力的高频成分显著增大。同时在高频段可辨识到频率为25.26、32.03和53.39 Hz的3个接触力分量，其对应波长分别为2.63、2.08和1.25 m，约等于二分之一定位点到吊弦的距离2.5 m、四分之一吊弦到吊弦的距离2 m和四分之一定位点到吊弦的距离1.25 m。同时在高频段出现了部分未能与接触网周期性结构和Zp对应的接触力分量。

通过对算例的分析可知：

(1)在曲线区段，随着列车运行速度的增加，接触力成分在高频段的能量变大，较短的结构参数如吊弦间距/定位点-吊弦间距的二分之一和四分之一对接触力的影响加剧，这与文献[38]中基于直线线路上的研究结果一致，证明接触力高频成分对接触力整体的影响不可忽视。

(2)在曲线区段，全频率段均出现了部分未能与接触网周期性结构和Zp对应的接触力成分，使接触力成分变得更加复杂

5 结论

本文介绍接触网和受电弓曲线区段建模过程，采用EN 50318标准对建模方法的有效性进行验证。通过对不同受电弓建模方案的可行性分析，发现采用忽略曲线特性的受电弓模型会导致Zp曲线波动变大，仿真结果失真，证明了曲线工况下弓网模型计及曲线特性的必要性。利用所建模型对曲线区段弓网的动态性进行研究，得到如下结论：

(1)在曲线区段，将接触线拉出值设置成恒定值有利于弓网获得更好的动态性能。当拉出值恒定设置后，拉出值的大小并不会对弓网动态性能产生明显影响，但该拉出值设置方式会明显减小受电弓的磨耗区域，加重受电弓的偏磨现象。

(2)由于接触线在世界坐标系下的垂向静态位移向受电弓局部坐标系转化的过程中变化幅度增大，导致曲线区段弓网的接触力标准差相较于直线区段上有所增大，动态性能出现了恶化。

(3)随着列车运行速度的增加，曲线区段弓网接触力高频成分能量显著增大，较短的接触网周期性结构参数对接触力分量的影响加剧，高频段的接触力分量不可忽略。传统评估标准中的0～20 Hz低频接触力指标难以全面反映曲线区段弓网的动态性能。同时，全频率段出现了小部分未能与接触网周期性结构和Zp对应的接触力分量，使接触力成分更加复杂。

研究结果表明，曲线区段的弓网系统在静态结构和动态性能两个方面均与在直线区段上有明显差距。未来的弓网设计与标准制定中，应增加对曲线工况的考虑。