横风作用对重载铁路桥上列车脱轨全过程的影响

龚 凯，刘林芽，向 俊，余翠英，刘全民，杨海明

(1.华东交通大学 轨道交通基础设施性能监测与保障国家重点实验室, 江西 南昌 330013；2.华东交通大学 铁路环境振动与噪声教育部工程研究中心, 江西 南昌 330013；3.中南大学 土木工程学院, 湖南 长沙 410075；4.华东交通大学 理学院, 江西 南昌 330013)

横风是影响铁路运营安全的重要因素之一，兰新线、青藏线等铁路干线常年受横风影响，著名的“百里风区”最高风速可达64 m/s[1-2]。因横风引起的脱轨事故时有报道[2]，2007年我国一列货物列车的集装箱因横风作用从墩高40 m桥上吹落；2008年美国俄亥俄州一列车过桥时因横风导致4节车厢落入水中；2015年，美国德克萨斯州一列车在跨越公路的桥梁上时因强风脱轨。可见，横风对桥上行车安全构成了严重威胁。不同于路基脱轨事故，桥上列车脱轨后易出现车辆冲出桥梁并掉落的二次事故，危害极大。

针对横风作用下桥上行车安全性问题，国内外学者开展了一些研究。Diana等[3]研究了横风作用下列车通过大跨度悬索桥时的振动响应。Cai等[4]探讨了车辆类型、车速、风荷载对车桥系统动力响应的影响。李小珍等[5]以五峰山长江大桥为例，研究了侧风作用下列车过桥时脱轨系数、轮重减载率、轮轴横向力等响应的变化规律，提出了不同风速下的车速阈值。郭向荣等[6]研究了满载和空载列车作用下横风对大跨度铁路斜拉桥及列车振动响应的影响，提出空载列车受横风影响显著。张骞等[7]采用脱轨系数、轮重减载率评价了列车通过沪通长江大桥时的行车安全性，提出风速25 m/s时行车安全性和舒适性满足要求。于梦阁等[8]将实测气动荷载作为外部激励，探讨了强横风作用下桥上高速列车的运行安全性。张田等[9]基于可靠度理论，探讨了桥上列车横风安全性的失效概率，提出风速、车速的增大会增加车桥系统的失效概率。陈克坚等[10]基于刚柔耦合法分析了风向角对车辆阻力系数、脱轨系数、轮重减载率等动力响应的影响，提出风向角90°时车辆动力响应最大。凌知民等[11]以某高墩连续刚构桥为例，采用脱轨系数、轮重减载率分析了横风作用下货物列车行车安全性。董天韵等[12]采用数值仿真计算，探讨了大风环境下列车横截面形状与车辆倾覆力矩间的关系。李德仓等[13]基于李亚普诺夫稳定性理论，设计了高速列车自动驾驶滑模自适应鲁棒控制器，对大风引起系统抖振起到控制作用。可是，现有研究针对横风作用大多提出了列车限速阈值，限速是控制行车安全的措施之一，但与当前社会对铁路运输能力的需求存在矛盾。实际上，实时监控行车状态，有效预报列车脱轨信息不失为一种主动的控制措施。预报脱轨信息，需判定列车是否脱轨，得到列车脱轨时的振动响应，并以此作为预警阈值的基础数据。而现有行车安全性评价指标难以在其超过限值时判定是否脱轨，无法反应脱轨信息[14]。

为此，本文基于货物列车-轨道-桥梁系统(FTTB系统)空间振动计算模型[15]，根据文献[16]，将横风作用转化为构架蛇行波，将其作为FTTB系统横向振动激振源，建立横风作用下FTTB系统空间振动计算模型；按照列车脱轨能量随机分析方法[14]，提出横风作用下重载铁路桥上列车脱轨全过程计算方法及列车脱轨预警原理，实现横风作用下桥上列车脱轨全过程计算，分析风速、车速对脱轨全过程中轮轨接触状态、轮轨相对位置及桥梁结构振动响应的影响，得到能够第一时间反映列车脱轨信息的轮轨相对位置，以此作为预警阈值基础数据，为研发横风作用下重载铁路桥上列车脱轨预警装置提供参考。

1 横风作用下FTTB系统空间振动计算模型

1.1 货物列车空间振动计算模型

货物列车假定作匀速运动，且前后、左右对称，以机车或车辆作为1个单元，可将列车划分为M个车辆单元，其中，每个单元离散为具有26个自由度的多刚体系统。车辆单元位移模式见表1。

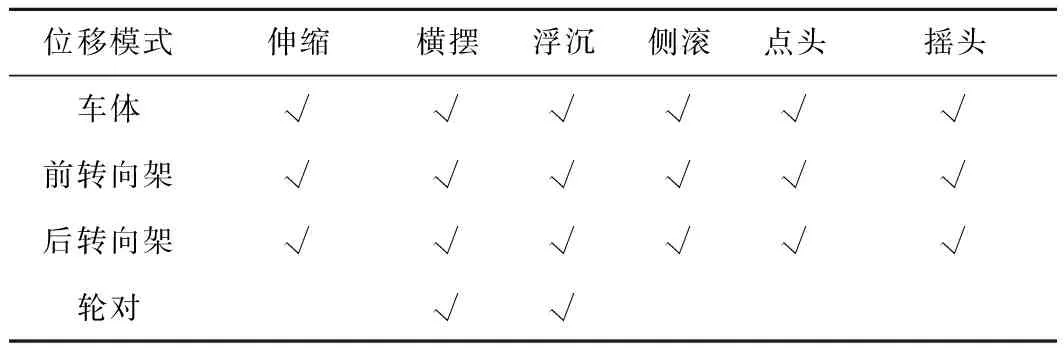
表1 车辆单元位移模式

根据表1位移模式，建立机车或车辆单元空间振动计算模型见图1。由图1可知，转向架与轮对之间的一系悬挂、车体与转向架之间的二系悬挂均采用线性弹簧和黏滞阻尼器联系，其中，转向架与轮对之间的X、Y、Z方向的弹簧系数和阻尼系数分别为K1X、K1Y、K1Z、C1X、C1Y、C1Z，车体与转向架之间的X、Y、Z方向的弹簧系数和阻尼系数分别为K2X、K2Y、K2Z、C2X、C2Y、C2Z。

基于上述假定，建立车辆单元空间振动位移模式公式为

δV=[Xc,Yc,Zc,θc,φc,ψc,Xt1,Yt1,Zt1,θt1,φt1,ψt1,Xt2,Yt2,

Zt2,θt2,φt2,ψt2,Yw1,Yw2,Yw3,Yw4,Zw1,Zw2,Zw3,Zw4]T

(1)

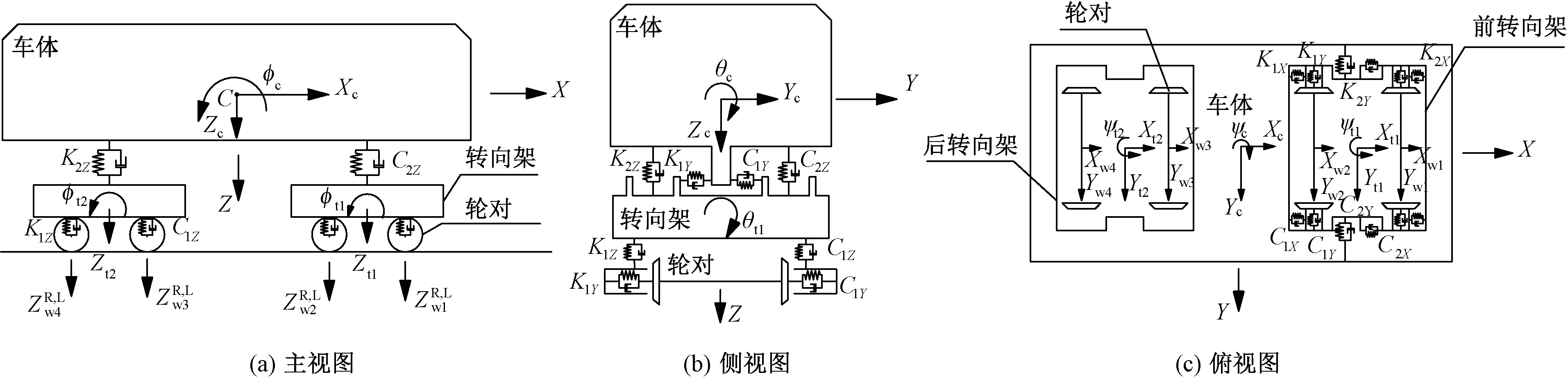
图1 机车或车辆单元空间振动计算模型

式中：X、Y、Z、θ、φ、ψ分别为纵向、横摆、浮沉、侧滚、点头、摇头位移；下标c、t1、t2分别为车体、前转向架、后转向架；Yw1、Yw2、Yw3、Yw4为轮对的横向位移；Zw1、Zw2、Zw3、Zw4为轮对的竖向位移。

根据上述位移模式，导出第i辆车的空间振动势能ΠVi，将桥上M辆车的空间振动势能叠加可得到货物列车空间振动总势能ΠV为[14]

(2)

1.2 轨道-桥梁系统空间振动计算模型

本文以重载铁路常见的单线预应力混凝土双T梁为例，将轨道结构放置于梁体上。钢轨、轨枕、梁体及墩体均采用梁单元模拟，其中，分别采用弹性点支承Euler梁和不考虑轴向变形的短梁模拟钢轨和轨枕，而梁体主要考虑横向、竖向位移及扭转，并假定T梁横向弯曲位移及转角相同，墩底固结；将钢轨与轨枕间的扣件、轨枕与梁体间的道砟、梁端与墩顶间的支座均模拟为线性弹簧和黏滞阻尼器，与扣件对应的弹簧系数和阻尼系数分别为K1、K2和C1、C2；与道砟对应的弹簧系数和阻尼系数分别为K4、K5和C4、C5；与支座对应的弹簧系数和阻尼系数分别为K6、K7和C6、C7。轨道-桥梁系统空间振动计算模型见图2。

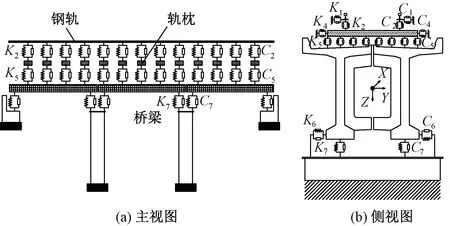
图2 轨道-桥梁系统空间振动计算模型

基于上述假定，以相邻横隔板为间距沿着梁跨方向将轨道、梁跨划分为n个梁段单元。每个梁段单元均离散为具有50个自由度的有限元模型，单元节点位移为

(3)

式中：1、2分别为梁段单元的左端和右端节点。

(4)

(5)

式中：U、V、W、θ分别为沿桥跨方向纵向、横向、竖向的线位移和转角位移；γ为钢轨沿线路纵向扭转角的变化率；上标T、S、B分别为钢轨、轨枕、桥梁主梁的位移；下标R、L分别为梁段单元的右侧和左侧；下标X、Y、Z分别为梁跨方向(纵向)、垂直于梁跨的水平方向(横向)、垂直于梁跨的竖直方向(竖向)；下标U、D分别为桥梁主梁的上翼缘和下翼缘。

根据式(3)中的单元节点位移，可导出梁段单元空间振动势能ΠTBj，将其叠加可得ΠTB，再与桥墩空间振动总势能ΠP叠加得到轨道-桥梁系统空间振动总势能ΠTB-P为[15,17-18]

ΠTB-P=ΠTB+ΠP

(6)

1.3 轮轨衔接条件

轮轨衔接条件是列车系统与轨道-桥梁系统之间的纽带。传统轮轨衔接条件是以轮轨密贴假定为主，即车轮与钢轨之间不发生相对运动，始终保持密贴，显然这与车轮实际运行的轨迹是不相符的。车轮之所以会出现脱轨掉道是因为车轮与钢轨之间发生了相对运动，当车轮轮缘由正常状态逐渐贴靠钢轨轨头，直至爬上钢轨顶部时，车轮发生脱轨，车轮爬轨过程见图3。

图3 车轮爬轨过程

要实现车轮脱轨，需要采用能够反映轮轨相对运动的衔接条件，即轮轨相对位移衔接条件为[14]

ΔYwr=Ywi-Yr-Yior

(7)

ΔZwr=Zwi-Zr-Zior

(8)

式中：ΔYwr、ΔZwr分别为轮轨横向、竖向相对位移；Ywi、Zwi分别为车轮横向、竖向位移；i为轮对个数，i=1～4；Yr、Zr分别为钢轨横向、竖向位移，由式(4)、式(5)通过节点位移插值函数求得[14]；Yior、Zior分别为轨道横向、竖向几何不平顺。同时，考虑轮轨“游间”的影响。

1.4 FTTB系统空间振动矩阵方程

设t时刻，在计算长度为L的重载铁路桥上，运行了一列车编组车辆数为M的货物列车，将货物列车空间振动势能ΠV与轨道-桥梁系统空间振动势能ΠTB-P叠加，即为FTTB系统空间振动总势能ΠVB，即

ΠVB=ΠV+ΠTB-P

(9)

对式(9)进行变分，可得

δΠVB=δΠV+δΠTB-P

(10)

针对式(10)，采用弹性系统动力学总势能不变值原理[19]，即δΠVB=0，按照形成系统矩阵的“对号入座”法则[20]，建立t时刻横风作用下FTTB系统空间振动矩阵方程为

(11)

1.5 横风作用下FTTB系统空间振动矩阵方程

现有研究[5-13]一般将横风作用作为外部激励，通过现场实测、数值仿真和室内试验得到结构气动特性，将气动特性转化为风荷载，施加于车体和梁体上，进而模拟横风作用。可是，本文因缺乏重载铁路桥梁在横风作用下的风荷载，故参考文献[16]，考虑列车风致振动特性及列车抖振反应谱的构架蛇行波标准差σpw，见图4。作为FTTB系统横向振动激振源，进而建立横风作用下FTTB系统空间振动计算模型，见图4。

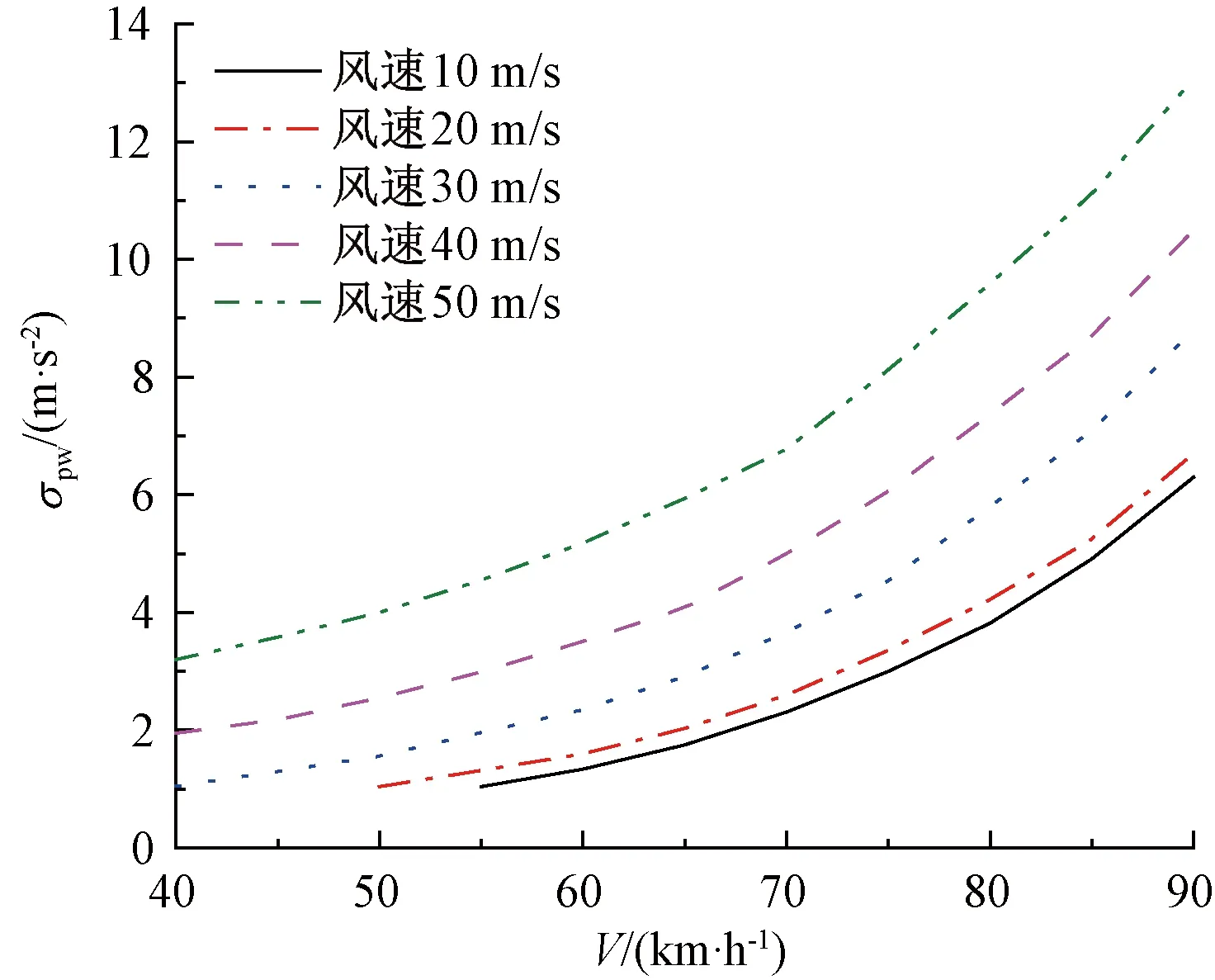
图4 横风作用下空载货车构架蛇行波标准差

根据图4，选取某一车速及风速下的σpw，采用Monte-Carlo法随机模拟一条构架蛇行波[14]，将其输入FTTB系统，作为考虑横风作用的FTTB系统横向振动激振源，并代入式(11)，则将式(11)中的矩阵进行分块，可得

(12)

式中：δs为s个已知位移；δn、Pn分别为n个未知位移和与其对应的荷载列阵。

将式(12)展开，可得

(13)

(14)

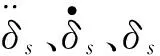
采用Wilson-θ逐步积分法，基于Fortran语言，通过编制程序可解出横风作用下FTTB系统空间振动响应；而式(14)为非独立方程，需要划去。

2 横风作用下重载铁路桥上列车脱轨全过程计算方法

反映列车脱轨信息需要研究列车脱轨全过程，研究列车脱轨全过程最直接的方式是开展脱轨试验。可是，现实中难以实现列车脱轨试验。为此，需要借助数值仿真计算，实现列车脱轨全过程计算。

列车脱轨机理表明[14]，列车脱轨是FTTB系统由小幅横向振动发展为大幅横向振动直至失稳的结果，而系统振动响应的增大亦是系统输入能量增大的结果。FTTB系统输入能量采用构架蛇行波标准差σp[14]，但这里的σp反映的是正常行车时FTTB系统的输入能量，无法实现列车脱轨全过程计算。

要实现列车脱轨全过程计算，需要得到使列车脱轨的FTTB系统输入能量σpn。实际上，根据压杆失稳临界荷载的计算过程可知，采用试算法[14]可以得到σpn，即假定比σp更大的σp1作为FTTB系统输入能量，得到的FTTB系统振动响应必然增大，当车轮最大悬浮量达到车轮脱轨几何准则(该准则是中国铁道科学研究院在开展单轮对车轮轮缘爬轨过程试验中，提出车轮悬浮量达到25 mm时，判定车轮脱轨)[14]时，就判定列车脱轨。此时的σp1是使列车脱轨的输入能量σpn。若σp1计算不出列车脱轨，则假定比σp1更大σp2作为FTTB系统输入能量，重复上述思路，直至试算出使列车脱轨的σpn。至此，完成列车脱轨全过程计算，相应的FTTB系统空间振动响应反映了列车脱轨全过程。此试算过程为列车脱轨能量随机分析方法[14]的基本思想。

由上述试算过程不难发现，σpn>σp，比σp更大的FTTB系统输入能量均有可能使列车脱轨。文献[16]将横风作用转化为FTTB系统输入能量，并对无风时车速V与σp的关系曲线进行了扩充，得到了不同风速下的σpw-V曲线，见图4。由图4可知，不同风速下的σpw均大于σp，即考虑横风作用的σpw可能会使列车脱轨，但无论这个能量是否能使列车脱轨。本文将其作为考虑了横风作用的FTTB系统输入能量，按照试算过程，提出横风作用下重载铁路桥上列车脱轨全过程计算方法，见图5。

图5 横风作用下重载铁路桥上列车脱轨全过程计算方法

3 列车脱轨预警原理

根据第2节的计算方法，实现横风作用下重载铁路桥上列车脱轨全过程计算，得到相应的FTTB系统空间振动响应，这些响应均可反映列车脱轨全过程。其中，轮轨接触状态和相对位置是反映列车脱轨瞬间行车状态最直接的指标。可是，因车辆底部空间狭小，车轮又为列车走行部分，将预警装置安装于车轮上易影响行车安全。为此，本文选取离车轮最近的转向架振动响应来反映轮轨接触状态及其相对位置，并将其作为描述列车脱轨预警阈值的指标，其状态见图6。

图6(a)为正常状态，车轮在钢轨之间运行；图6(b)为脱轨状态，一侧车轮已爬上钢轨顶部，另一侧车轮从钢轨上掉落。随着车轮爬上钢轨顶部，转向架发生了相应的位移，考虑列车行驶中，钢轨产生振动响应。为此，以列车脱轨瞬间转向架与钢轨间的横向相对位移ΔYtr作为反映轮轨接触状态的指标，并参考日本学者用脱轨系数计算列车安全性时采用1.25作为安全系数[21]，将ΔYtr/1.25作为反映列车脱轨信息的预警阈值(在图6中，粉色虚线表示线路中心线，蓝色虚线表示转向架中心线)。

图6 转向架行驶状态

4 实例分析

4.1 横风作用下列车脱轨全过程计算

鉴于列车脱轨多以空车为主[6,14,22]，本文列车编组为1辆机车牵引16辆空载敞车，计算车速为60 km/h。轨道结构为：60 kg/m钢轨，Ⅱ型混凝土轨枕，碎石道砟。梁跨结构采用32.0 m预应力混凝土T梁桥，梁型为参标桥2019，直线桥；桥墩采用圆形墩，墩高10.0 m，横截面直径为2.4 m。以7跨32.0 m预应力混凝土简支梁单线桥作为计算对象。研究表明，我国青藏线沿线年平均大风日为115～160 d，最大风速为20～28 m/s[23]。本节以大风风速范围[24]为例，计算风速为28.4 m/s。

基于上述参数及计算方法，计算横风作用下重载铁路桥上列车脱轨全过程，得到FTTB系统空间振动响应。本节列出了车轮悬浮量ΔZ、脱轨系数Q/P、轮重减载率ΔP/P、转向架与钢轨横向相对位移ΔYtr、梁跨跨中横向位移Bh及墩顶横向位移Dh等时程曲线。

第11车第4轴右轮悬浮量ΔZ时程曲线见图7。由图7可知，随着横坐标时间t的增大，车轮悬浮量出现动态变化；当横坐标时间t=18.77 s时，车轮悬浮量最大，达到25 mm。此时，判定列车脱轨。

图7 第11车第4轴右轮悬浮量时程曲线

第11车第4轴右轮脱轨系数Q/P和轮重减载率ΔP/P时程曲线见图8。由图8可知，列车未脱轨时，Q/P和ΔP/P最大分别为11.85和0.73，均超过规范限值1.2和0.65[25]；列车脱轨瞬间，Q/P和ΔP/P分别为1.84和0.67，也均超过规范限值要求[25]。可见，脱轨系数和轮重减载率难以确保在列车行驶中不超过规范限值。

图8 第11车第4轴右轮脱轨系数和轮重减载率时程曲线

第11车后转向架与钢轨横向相对位移ΔYtr时程曲线见图9。由图9可知，随着横坐标时间t的增大，ΔYtr在0线附近交替出现正负变化，0线表示轨道中心线。可见，列车在行驶中的蛇行运动状态。当列车脱轨时，ΔYtr=63.1 mm，该值反映了车轮脱轨瞬间轮轨接触状态。

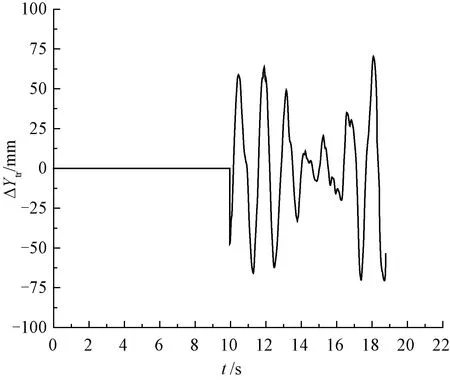
图9 第11车后转向架与钢轨横向相对位移时程曲线

由图7～图9知，第11车第4轴右轮进桥的起始时间t=9.4 s，终止时间t=18.77 s，车轮行驶时间t=9.37 s；又根据车速60 km/h，计算得到车轮在桥上行驶距离为60/3.6×(18.77-9.4)=156.16 m。前已说明计算桥跨数为7跨，那么，桥上5跨距离之和为160 m，156.16 m<160 m。可见，第11车第4轴右轮运行至第5跨时发生脱轨。因此，这里给出第5跨跨中横向位移Bh及第5跨右墩(即沿X方向的梁跨右端)墩顶横向位移Dh时程曲线见图10。

由图10可知，随着时间t的增大，Bh和Dh逐渐增大，这是因为经过第5跨的车辆数逐渐增多导致。同时，振动响应的增大，也反映了系统输入能量的增大。在列车脱轨瞬间，Bh、Dh分别为9.7、3.2 mm。可见，列车脱轨亦会引起桥梁结构振动响应增大。

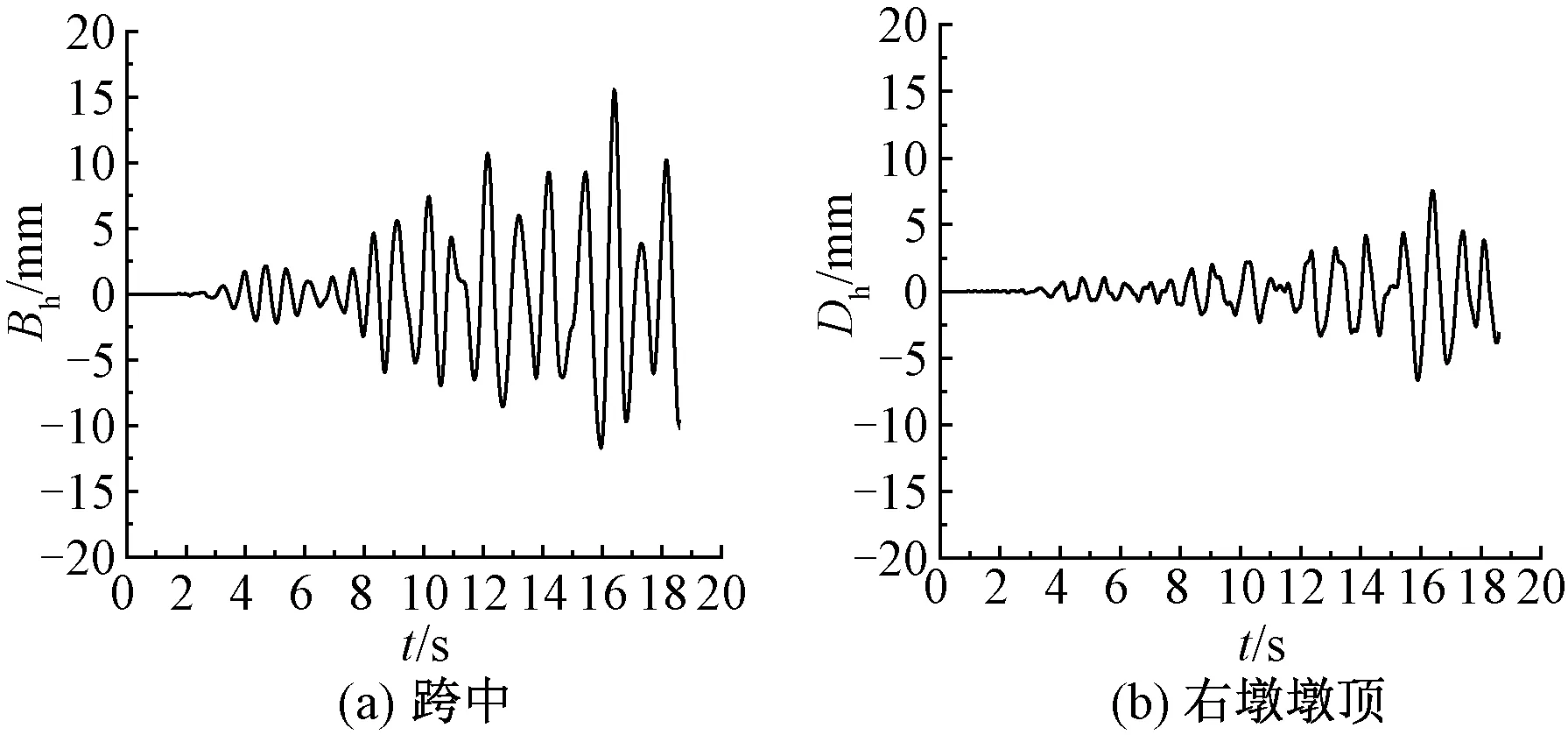
图10 第5跨不同位置横向位移时程曲线

4.2 风速及车速对列车脱轨全过程的影响

为进一步分析列车脱轨全过程随风速及车速的变化规律。本节列车计算编组、轨道及桥梁结构与4.1节一致。计算车速V为60～80 km/h；鉴于大风风速范围[24]，计算风速Vw分别为20.7、24.4、28.4 m/s。基于上述参数及计算方法，计算不同风速、车速下列车脱轨全过程，将得到的列车脱轨瞬间车轮悬浮量ΔZ、脱轨系数Q/P、轮重减载率ΔP/P、转向架与钢轨横向相对位移ΔYtr、梁跨跨中横向位移Bh及墩顶横向位移Dh等计算结果见表2，其随风速及车速的变化见图11～图15。

由表2可知，当车速60～80 km/h、风速20.7～28.4 m/s时，车轮悬浮量均达到25 mm，判定列车脱轨。脱轨车辆、车轴及车轮见表2。

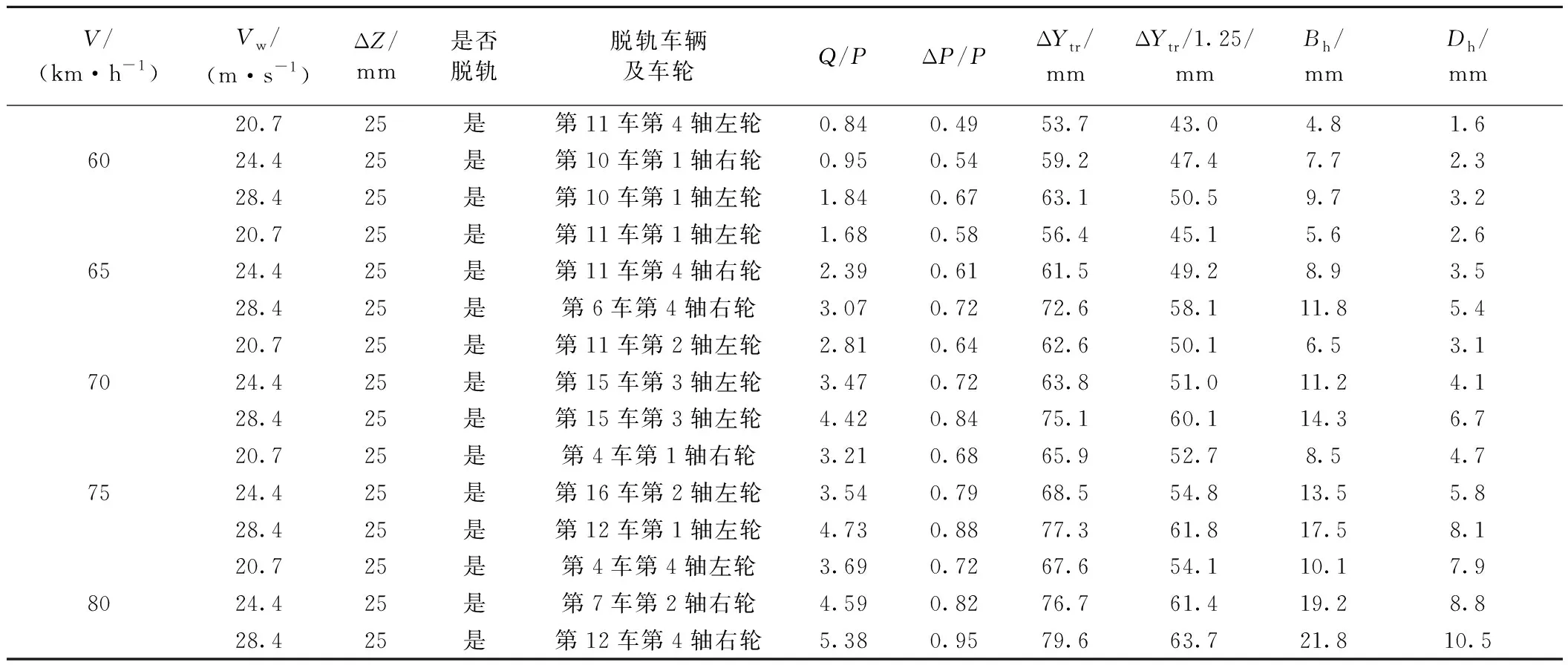
表2 不同风速下重载铁路桥上货物列车脱轨全过程计算结果

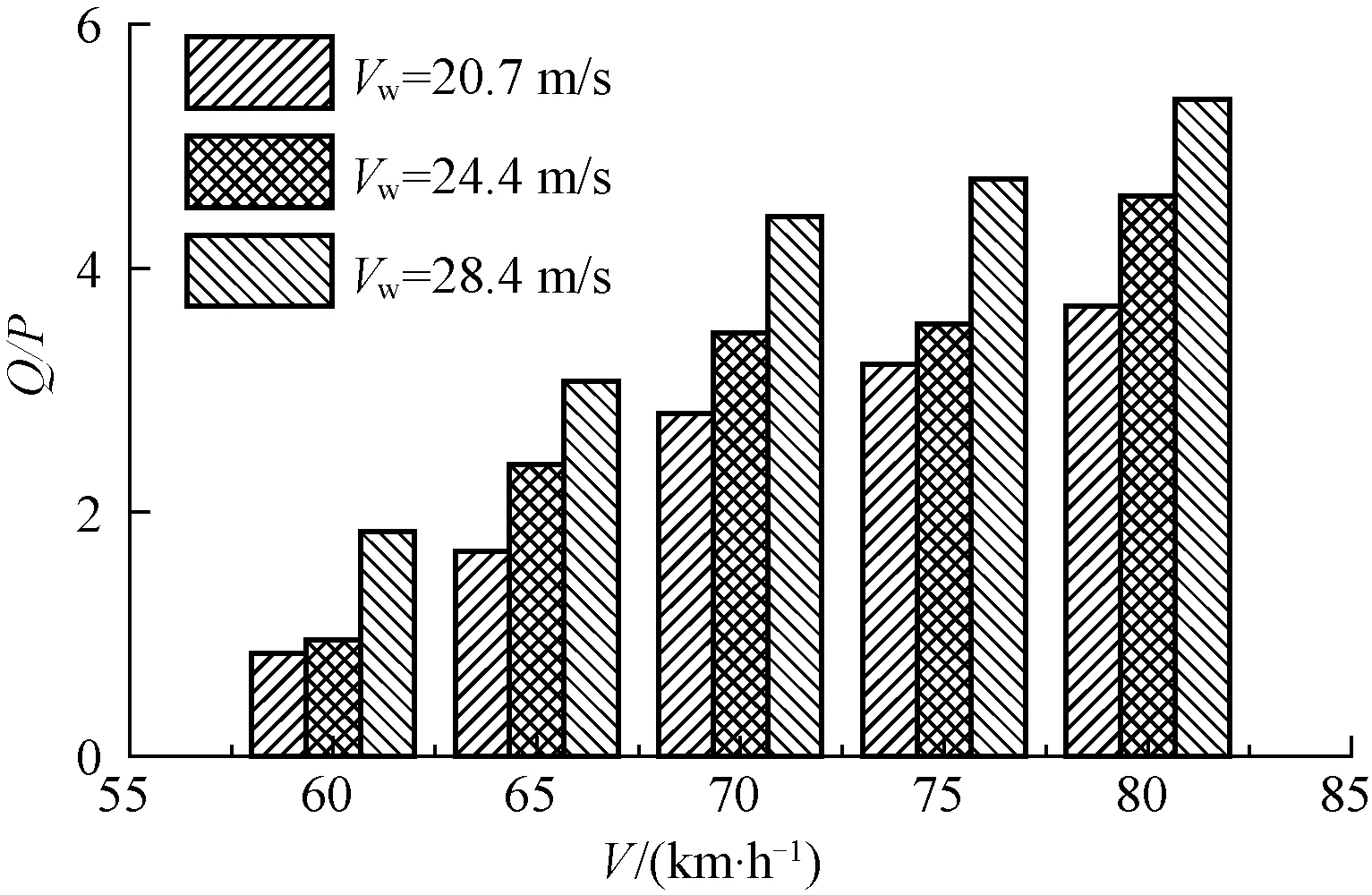
图11 脱轨系数随风速及车速的变化

由图11可知，当风速为28.4 m/s时，不同车速下的Q/P分别为1.84、3.07、4.42、4.73、5.38，相比车速60 km/h，车速80 km/h时Q/P增大了1.92倍；当车速为80 km/h时，不同风速下的Q/P分别为3.69、4.59、5.38，相比风速20.7 m/s，风速28.4 m/s时，Q/P增大了0.45倍。可见，车速及风速对脱轨系数影响显著。并且，车速60 km/h，风速20.7、24.4 m/s时，Q/P分别为0.84、0.95，均未超过规范限值[25]。由此进一步说明，脱轨系数未超限时，列车也会出现脱轨。

图12 轮重减载率随风速及车速的变化

由图12可知，当风速为28.4 m/s时，不同车速下的ΔP/P分别为0.67、0.72、0.84、0.88、0.95，相比车速60 km/h，车速80 km/h时ΔP/P增大了0.42倍；当车速为80 km/h时，不同风速下的ΔP/P分别为0.72、0.82、0.95，相比风速20.7 m/s，风速28.4 m/s时，ΔP/P增大了0.32倍。尽管，轮重减载率增幅不大，但是车轮减载程度显著增大，最大接近1.0(即车轮完全减载)。同时，车速60 km/h、风速20.7、24.4 m/s时，ΔP/P分别为0.49、0.54，均未超过规范限值[25]。由此说明，轮重减载率未超限时，列车会出现脱轨。

图13 转向架与钢轨横向相对位移随风速及车速的变化

由图13可知，当风速为28.4 m/s时，不同车速下的ΔYtr分别为63.1、72.6、75.1、77.3、79.6 mm，相比车速60 km/h，车速80 km/h时ΔYtr增大了0.26倍；当车速为80 km/h时，不同风速下的ΔYtr分别为67.6、76.7、79.6 mm，相比风速20.7 m/s，风速28.4 m/s时，ΔYtr增大了0.18倍。可见，转向架与钢轨横向相对位移随车速及风速的增大而增大。同时，基于列车脱轨瞬间的ΔYtr，考虑安全系数1.25，得到了不同车速及风速下具有脱轨信息的预警阈值ΔYtr/1.25，具体数值见表2。

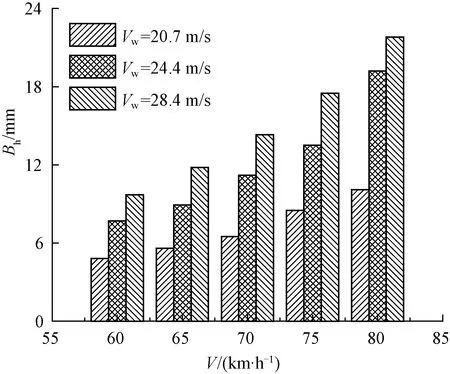
图14 梁跨跨中横向位移随风速及车速的变化

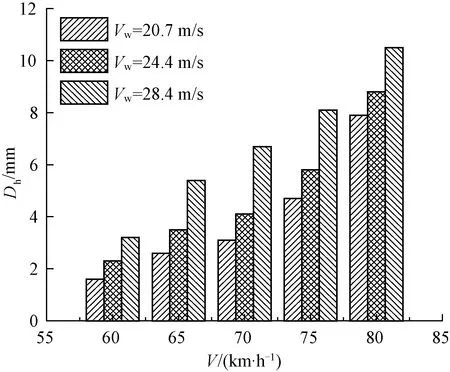
图15 桥墩墩顶横向位移随风速及车速的变化

由图14可知，当风速为28.4 m/s时，不同车速下的Bh分别为9.7、11.8、14.3、17.5、21.8 mm，相比车速60 km/h，车速80 km/h时Bh增大了1.25倍；当车速为80 km/h时，不同风速下的Bh分别为10.1、19.2、21.8 mm，相比风速20.7 m/s，风速28.4 m/s时，Bh增大了1.16倍。同时，由图15可知，当风速为28.4 m/s时，不同车速下的Dh分别为3.2、5.4、6.7、8.1、10.5 mm，相比车速60 km/h，车速80 km/h时Dh增大了2.28倍；当车速为80 km/h时，不同风速下的Bh分别为7.9、8.8、10.5 mm，相比风速20.7 m/s，风速28.4 m/s时，Dh增大了0.32倍。可见，车速及风速对梁跨跨中横向位移及墩顶横向位移均有较大影响。

5 结论

本文建立了横风作用下FTTB系统空间振动计算模型，提出了横风作用下重载铁路桥上列车脱轨全过程计算方法，实现了列车脱轨全过程计算，分析了列车脱轨全过程中的轮轨接触状态、轮轨相对位置及桥梁结构振动响应。主要结论如下：

(1)车速60～80 km/h、风速20.7～28.4 m/s时，车轮悬浮量均达到25 mm，判定列车脱轨。

(2)当风速为28.4 m/s时，相比车速60 km/h，车速80 km/h对应的脱轨系数增大了1.92倍；当车速为28.4 m/s时，相比风速20.7 m/s，风速28.4 m/s对应的脱轨系数增大了0.45倍。车速及风速对脱轨系数影响显著，并且脱轨系数即使未超过限值，列车也会脱轨。

(3)当风速为28.4 m/s时，相比车速60 km/h，车速80 km/h对应的轮重减载率增大了0.42倍；当车速为28.4 m/s时，相比风速20.7 m/s，风速28.4 m/s对应的轮重减载率增大了0.32倍。车速及风速对轮重减载率具有一定的影响，且车轮减载程度较大，最大值接近1.0(即完全减载)。同样的，当轮重减载率未超过限值时，列车也发生了脱轨。

(4)当风速为28.4 m/s时，不同车速下相比车速60 km/h，车速80 km/h时转向架与钢轨横向相对位移增大了0.26倍；当车速为80 km/h时，相比风速20.7 m/s，风速28.4 m/s时，相对位移增大了0.18倍。转向架与钢轨横向相对位移随着车速的增大而增大，并计算得到了考虑安全系数1.25后的转向架与钢轨横向相对位移，将其作为反映列车脱轨信息的预警阈值。

(5)当风速为28.4 m/s时，相比车速60 km/h，车速80 km/h时Bh和Dh分别增大了1.25倍和2.28倍；当车速为80 km/h时，相比风速20.7 m/s，风速28.4 m/s对应的Bh和Dh分别增大了1.16倍和0.32倍。车速及风速对梁跨跨中及墩顶横向位移影响均较大。