定位点分布对相机位姿解算精度影响分析

王高杰，郝向阳，欧阳文，郑 凯，李朋月

（信息工程大学 地理空间信息学院，郑州 450000）

0 引言

基于单目相机的视觉导航过程，需要进行相机位姿的实时解算。使用人工标志的视觉导航方式，需要通过识别人工标志获取精确的3 维点，利用物点与像点的透视关系式解算出相机中心相对于世界坐标系的位置和姿态，是视觉导航1 种重要的手段。在人工标志无法密集布设的情况下，标志点的分布对于相机位姿估计具有一定的影响；分析定位点的构型与位姿解算精度的关系，对于设计更加实用准确的人工标志分布方案，以及位姿解算过程中的点位选择真有重要意义。

目前受限于计算机技术的发展，无论对室内导航还是室外导航，都很难进行高速率的场景建模。因此，广泛运用基于人工地标的识别定位方法来实现定位[1]。当前比较有代表性的是由密西根大学阿普里尔（April）实验室开发的阿普里尔·塔格（AprilTag）视觉基准系统[2]。AprilTag 可以识别单个或者多个人工标志，很好地解决了传统的人工标志受环境、光照等条件影响时，识别出错率较高的问题，可以进一步提升识别效率与定位精度[3]；但是实现这一目标对于AprilTag 标志布设的要求比较高。

本文使用精确标定的相机获取图像信息，在奥普蒂·特拉克（OptiTrack）运动捕捉系统下，获得准确的人工标志定位点坐标以及相机中心的概略位置和相机姿态，重点研究人工标志定位点的分布对于单目位姿解算精度的影响，并对视觉导航过程中，人工标志的布设，以及位姿解算过程中，点位的选择提出合理的方案和建议。

1 原理及流程

本节对相机标定、标志点坐标提取、n 点透视问题（n point perspective problem，PnP）和点位构型的描述进行介绍。实验流程如图1 所示。

图1 实验流程

主要包括相机的标定、标志点准确3 维坐标的获取、图像中定位点坐标的提取、相机位姿的解算和精度的分析。

1.1 相机标定

实验中采用Canon 65X 相机，拍摄照片的分辨率为3 264×2 448 个像素。文献[4]的相机标定方法，相对于其他标定方法，具有操作简单、标定板制作容易、对应点匹配简单等特点，因而本文主要采用张正友相机标定方法。文献[4]相机标定流程如下：读取相机拍摄的棋盘格照片、提取角点并绘图、生成角点像素坐标、最大似然求单应矩阵、建立约束方程、奇异值分解（singular value decomposition,SVD）得唯一解、乔列斯基（Cholesky）分解得到内参矩阵、计算外参数矩阵、标定完成。

如图2 所示，从不同角度拍摄12 张棋盘格照片，利用开源计算机视觉库（OpenCV）中的标定函数calibrateCamera 进行相机标定。输入的参数包括：12 张棋盘格照片路径，棋盘格大小8×11 格，棋盘格每个单元宽度为20 mm。

图2 棋盘格照片

相机标定结果如表1 所示。

表1 相机标定结果

表1 中：fx和 fy为x 和y 方向上的焦距；u0和 v0为像主点坐标；k1和 k2为径向畸变系数；重投影误差为0.181 4 个像素。

标定结果精度较高，满足实验的要求。

1.2 OptiTrack 运动捕捉系统

OptiTrack 是基于多相机的运动捕捉系统，在相机标定以及系统坐标系建立完成之后，对于空间中的1 个点，如果它能同时为2 部摄像机所见，则根据同一时刻2 部摄像机所拍摄的图像和摄像机参数，可以确定这一点在空间中的位置，精度可达到亚毫米级[5]。OptiTrack 系统如图3 所示。本文实验使用反光标志球代替人工标志的定位点，通过OptiTrack 系统获得标志点的准确空间位置以及相机中心的大致位置和相机姿态。

图3 OptiTrack 系统

首先，对OptiTrack 系统进行初始化标定，系统6 个相机视场采样点如图4 所示，标定好的系统如图5 所示。

图4 OptiTrack 系统标定时相机视场采样点

图5 标定好的OptiTrack 系统

在空间中密集布设反光标志球作为定位点，为相机位姿的解算提供准确的物点坐标。

1.3 PnP 问题

文献[6]于1981 年首先提出n 个3D 空间点求解相机位姿问题，也称为PnP 问题。PnP 问题就是指如下的物体定位问题：假设相机模型为小孔模型，相机已完成标定过程，如果有1 幅在物体坐标系下坐标已知的n 个空间点的照片，且这n 个图像点的像素平面坐标为已知，确定这n 个空间点在相机坐标系下的坐标。PnP 算法的目的，是利用人工标志的位置信息、人工标志上特征点之间的位置关系以及提取到的特征点坐标和相机内参数，来解算相机坐标系和世界坐标系之间的相对位姿。

本文使用OpenCV 中的solvePnP 函数进行相机位姿的解算，solvePnP 函数里有4 种解法：透视3 点算法（perspective-three-point, P3P）、高效透视n 点算法（efficient perspective-n-point, EPnP）、迭代法和直接最小二乘方法（direct least-squares, DLS）。

DLS 适用于定位点较多的情况，根据文献[7]，在标志点密集布设、照片中标志点足够多、标志点3维坐标精度小于1 mm、相机焦距标定精度20 μm、像点提取的误差为0.5 个像素时，位置计算的精度可以达到毫米级，姿态计算精度不超过1′，可以满足实验的要求。

P3P 算法[8]使用3 对点求解旋转角和平移向量，利用第4 个已知点对来验证得到的位姿，虽然依赖于线性模型，对系统精度要求较高，但是在没有较大误差时能够得到较好的结果。

EPnP 算法[9]充分挖掘位姿估计中特有的约束，引入适当中间变量来表示点集，将问题在尽量减少信息损失情况下，转换为绝对定向问题，进而得到闭式解法，EPnP 算法是目前稳定高效的PnP问题解法。对于世界坐标系下的标志点w( , ,iP i=1 2… , n)和相机坐标系下的对应点 PiC(i =1, 2,… , n)，可以构造 1 组虚拟的控制点 Viw(i =1, 2,…, n)来表示，即：

式中 ViC为 Viw在相机坐标系下的坐标。所以，在求出 ViC后，问题便转化为绝对定向问题，即

式中： R为世界坐标系相对于相机坐标系的旋转矩阵；t为世界坐标系相对于相机坐标系的平移向量。

迭代法选择像方残差或者物方残差作为目标函数，不断优化求解，得到高精度的位姿解算结果，即

式中Vi=O′O′T/O′TO′，O为权矩阵。不断迭代求解R和t，当相邻2 次计算的目标函数差值小于给定的阈值时，结束运算，此时的R和t为最优解。基于各种算法的特点，使用DLS 算法以及全部定位点解算相机的位姿真值，分别使用P3P、EPnP 和迭代算法计算定位点不同分布情况下，相机位姿解算的结果，并进行精度的评定和分析。

1.4 定位点分布的表达方式

为描述空间中定位点相对于相机的分布情况，参考卫星导航定位中精度衰减因子（dilution of precision, DOP）的定义[10]。对于EPnP 和迭代法，采用4 个定位点进行相机位姿解算时，系数矩阵表达为

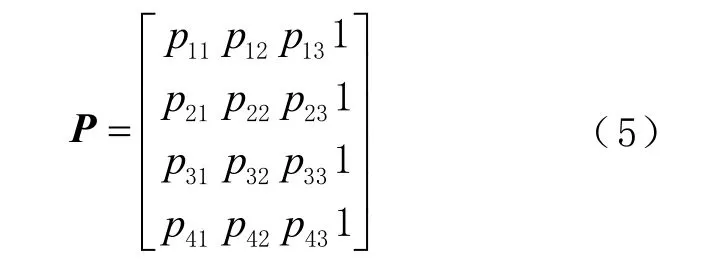
式中 p（iji = 1, 2, 3, 4；j =1, 2, 3）表示相机与定位点之间方向矢量的余弦。

由最小二乘知，定位误差的协因数阵为

式中 q（iji = 1, 2, 3, 4；j =1, 2, 3, 4）为i 点与j 点的互协因数。

本文选择PDOP 来描述定位点的分布情况，即

对于P3P 算法，采用4 个定位点进行相机位姿解算时，只考虑前3 个点的构型，系数矩阵具体表达为

由最小二乘知，定位误差的协因数阵为

PDOP 的计算方式为

2 结果及分析

2.1 相机相对位姿的解算

首先通过相机拍摄的棋盘格照片进行相机标定，在OptiTrack 系统中布设反光标志球，记录反光标志准确的空间3 维坐标作为物点的真实坐标，而后采用相机拍摄反光标志照片，手动提取出定位点的像素平面坐标，利用OpenCV 函数库进行相机相对位姿的解算。实验过程中，通过改变相机的位置或者反光标志的分布情况，研究定位点分布对于位姿解算精度的影响。

2.2 相机位置解算精度分析

选择3 个实验场景进行数据分析。图6、图7、图8 依次为场景1、场景2、场景3 的布设情况。场景1、场景2 和场景3 中，相机距离定位点概略距离分别为1.6、2.5 和1.9 m，场景1 和场景2 中设置8 个定位点，场景3 中设置12 个定位点，同一场景中，定位点分布在不同平面上并保持一定距离。

图6 场景1 布设情况

图7 场景2 布设情况

图8 场景3 布设情况

在3 个实验场景下，针对所有的定位点组合计算对应的PDOP 值，分别使用P3P 算法、EPnP 算法以及迭代法计算相机位置，选择正确的解算结果，分析各个方向上定位误差以及整体定位误差与PDOP 值之间的关系。

每个场景下相机的位置以及3 种解算方法得到的数据情况如表2 所示。

表2 相机的位置信息

4 个定位点的不同分布对应不同的PDOP 值，以场景1 为例，EPNP 算法各个方向上的误差具体分布情况如图9 所示；P3P 算法各个方向上的误差具体分布情况如图10 所示；迭代算法各个方向上的误差具体分布情况如图11 所示。

图9 EPnP 算法3 个方向上的定位误差随PDOP 值变化

图10 P3P 算法3 个方向上的定位误差随PDOP 值变化

图11 迭代算法3 个方向上的定位误差随PDOP 值变化

由图9～图11 可知：在PDOP 值较小即定位点构型良好的时候，各个方向的定位误差都较小，但没有明显的规律，这是由于受到了像点提取误差、相机焦距误差等误差的影响；EPnP 算法和迭代算法中PDOP 值小于10 的点各个方向上的定位误差均小于10 mm，所占的比例超过了90%，P3P 算法中PDOP 值小于40 的点各个方向上的定位误差均小于40 mm，所占的比例超过了95%，随着PDOP值的增大，3 种方法计算得到的3 个方向上的定位误差均变大，说明定位点的构型会对位置解算的精度产生影响。

使用3 种算法在3 个场景下的整体定位精度随着PDOP 值的变化情况分别如图12～图14所示。

图12 场景1 中3 种算法定位整体误差随PDOP 值变化情况

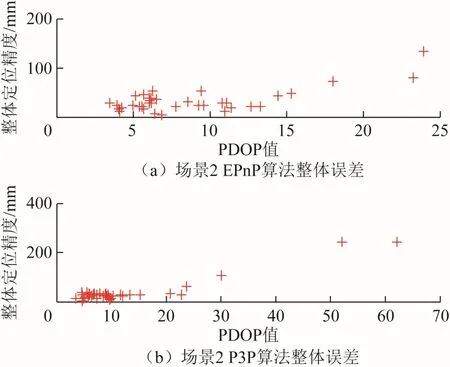
图13 场景2 中3 种算法定位整体误差随PDOP值变化情况

图14 场景3 中3 种算法定位整体误差随PDOP 值变化情况

图中的整体定位误差表示定位点的真实坐标与位姿解算得到的坐标之间的几何距离。图12～图14表明：在PDOP 值较小的情况下，定位整体误差受到像点提取误差等其他因素的影响，误差分布没有明显的规律，但随着PDOP 值的增大，定位误差整体呈现增大的趋势，进一步说明了定位点的构型会对位置解算精度产生影响，且2 者呈正相关。

在3 个场景中，相机与定位点的距离有一定差异，为研究距离对于相机位姿解算精度的影响，对比分析同种算法在3 个不同场景中，相机定位整体误差随PDOP 值变化的情况。利用1 组或几组定位点组合来解算相机位置受到其他因素如相机标定误差、定位点提取误差等的影响，得到的结果受偶然因素影响并不可靠，所以对比分析同种算法在3 个场景下，整体定位误差随PDOP 值的变化情况，为保证数据的可靠性，将PDOP 值限定在合理范围之内。使用EPnP 算法时整体定位误差随PDOP 值变化情况如图15 所示；使用P3P 算法时，整体定位误差随PDOP 值变化情况如图16 所示；使用迭代算法时，整体定位误差随PDOP 值变化情况如图17 所示。

图15 EPnP 算法整体定位误差随PDOP 值变化情况

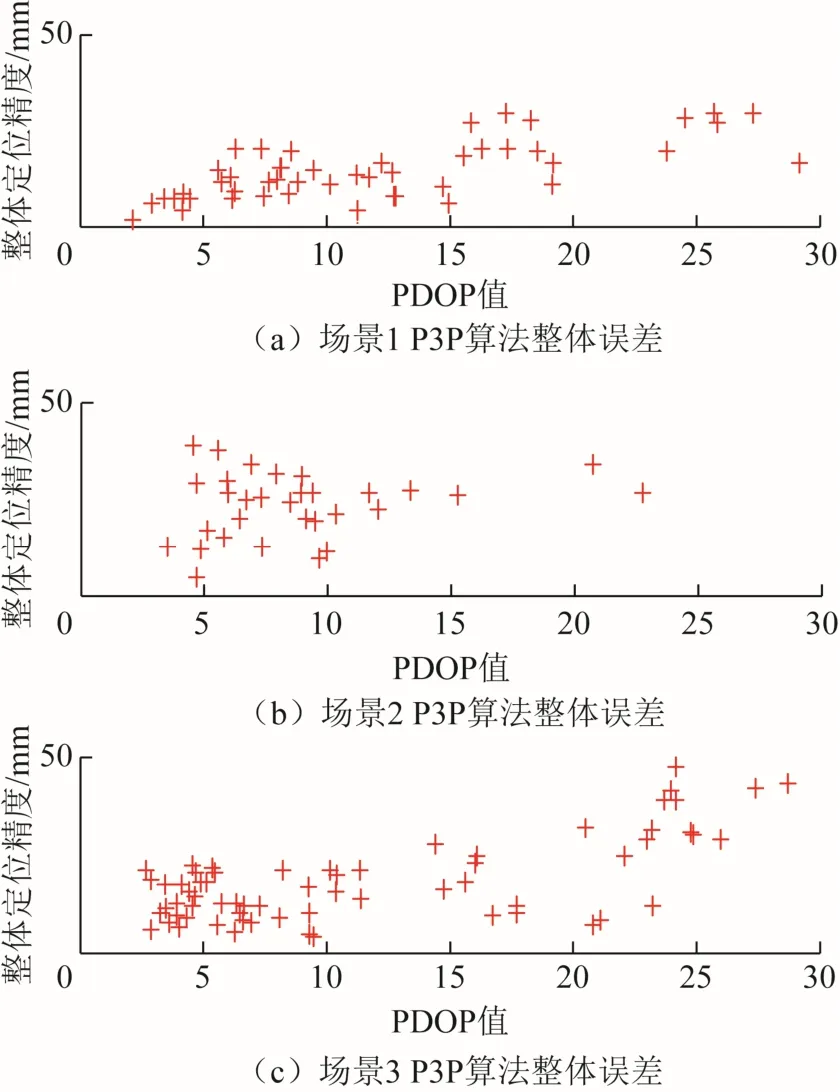
图16 P3P 算法整体定位误差随PDOP 值变化情况

图17 迭代算法整体定位误差随PDOP 值变化情况

如图15～图17 所示：使用EPnP 算法计算3 个场景中相机的位置后，取PDOP 小于16 的数据部分进行分析，场景1 中93.3%的结果整体定位误差小于20 mm，场景2 中31.2%的结果整体定位误差小于20 mm，场景3 中43.7%的结果整体定位误差小于20 mm；使用P3P 算法计算3 个场景中相机的位置后，取PDOP 小于30 的数据部分进行分析，场景1 中77%的结果整体定位误差小于20 mm，场景2 中32.2%的结果整体定位误差小于20 mm，场景3 中59%的结果整体定位误差小于20 mm；使用迭代算法计算3 个场景中相机的位置后，取PDOP 小于30 的数据部分进行分析，场景1 中87.5%的结果整体定位误差小于20 mm，场景2 中50%的结果整体定位误差小于20 mm，场景3 中75%的结果整体定位误差小于20 mm。

根据相机在系统坐标系下的真实位置及定位点的分布情况，场景1 中相机与定位点的距离最近，场景2 中相机与定位点距离最远。由以上分析可知，在PDOP 值较小的情况下，3 种算法分别计算得到的相机位置整体误差均体现为：场景1 中整体定位误差最小，场景3 中整体定位误差次之，场景2 中整体定位误差最大。所以相机与定位点之间的距离，对整体定位误差产生影响，且在一定范围内，距离越小整体定位误差越小。

2.3 相机姿态解算精度分析

在场景1 中，针对所有的定位点组合计算对应的PDOP 值，分别使用P3P 算法、EPnP 算法以及迭代法计算相机姿态，选择正确的解算结果，分析俯仰角、方位角、横滚角误差与PDOP 值之间的关系。

4 个定位点的不同分布对应于不同的 PDOP值，EPnP 算法解算结果，角度误差随PDOP 值的变化情况如图18 所示；P3P 算法解算结果，角度误差随PDOP 值的变化情况如图19 所示；迭代算法解算结果，角度误差随 PDOP 值的变化情况如图20 所示。

图18 EPnP 算法姿态角误差随PDOP 值变化

图19 P3P 算法姿态角误差随PDOP 值变化

图中的姿态角误差表示姿态角真值与解算结果差的绝对值。图18～图20 表明：在PDOP 值小于20 的情况下，3 种算法解算的姿态角误差小于1°的所占比例高于92%，在此范围内，误差分布和PDOP 值没有明显的规律，但随着PDOP 值的增大，姿态角解算误差整体呈现增大的趋势，说明了定位点的构型会对姿态解算精度产生影响，且2 者呈正相关。

图20 迭代算法姿态角误差随PDOP 值变化

根据实验结果，人工标志的布设应充分考虑点位的分布情况，尽量避免过于密集的布设，应依据现场环境的情况、相机与人工标志的距离和角度、人工标志的最大识别距离等情况进行标志布设，使得邻近的标志点构型良好，保证每张照片中都存在至少4 个构型良好的标志点；照片包含标志点较多时，可以考虑根据相机的概略位置，选择构型良好的标志点进行位姿解算，以提高解算精度。

3 结束语

视觉传感器具有廉价、信息丰富、易于获得等特点，视觉导航是今后导航定位领域的热点问题。本文使用精确标定的相机获取图像信息，提取出标志点的像点坐标，在OptiTrack 运动捕捉系统下，获得准确的人工标志定位点坐标，进行相机位姿的解算，研究人工标志定位点的分布对于单目位姿解算精度的影响。实验结果表明：当PDOP 值较小时，位姿解算精度主要受像点提取误差、相机标定误差等误差的影响，但当 PDOP值大于一定阈值时，随着PDOP 值增大，位姿解算误差持续增大，定位点的构型成为影响位姿解算精度的主要原因；在一定范围内，相机与定位点之间的距离越小，定位误差越小。