UWB 测距室内定位算法误差分析
张 媛,缪相林,王 梅,丁 凰
(1.西安交通大学 城市学院,西安 710018;2.西安交通大学 计算机科学与技术学院,西安 710049)
0 引言
如今,室外定位系统已经发展的非常成熟,如美国的全球定位系统(global position system, GPS)[1]、我国的北斗卫星导航系统(BeiDou navigation satellite system, BDS)以及欧盟的伽利略卫星导航系统(Galileo satellite navigation system, GSNS)。这些定位系统在室外具有较准确的定位性能,但是它们在室内环境下,则无法完成定位。而现今,室内定位已成为传感网络的最主要的议题[2-4]。
为了提高室内定位精度,研究人员提出了一些局部定位系统(local positioning system, LPS)。例如:文献[5]将无线保真(wireless fidelity, WiFi)定位技术应用到复杂的室内环境中;文献[6-7]采用射频识别(radio frequency identification, RFID)标签进行室内定位。尽管基于WiFi 和RFID 的LPS技术已经在室内环境中广泛使用,但是它们只能提供米级的定位精度。
为了获取更高的定位精度,研究人员把目光投向超宽带(ultra wide band, UWB)技术。例如,文献[8]利用UWB 技术跟踪室内环境的目标。UWB信号频带宽范围为3.1~10.6 GHz,宽的频带性能使其具有极窄的脉冲,时间分辨率高,穿透性强,适合室内环境定位。此外,相比于其他技术,UWB 技术的功耗也小。
目前,研究人员针对UWB 定位系统,提出了不同的定位算法。例如:文献[9]提出了融合UWB测距信息的室外高精度定位算法,根据车辆行驶航迹,并结合UWB 测距信息估计车辆位置。文献[10]提出了改进双向测距到达时间差定位算法的超宽带定位系统,利用双向测距并通过线性处理,提高定位精度。通常,基于UWB 定位算法,首先利用UWB 测距,然后再利用这些测距值,并结合定位算法估计节点位置。这些算法包括线性最小均方误差估计(linearized least square estimation,LLSE)、指纹估计(finger print estimation, FPE)、加权质心估计(weighted centroid estimation, WCE)等。
这些定位算法的定位特性存在差异,在不同的环境下,定位性能并不相同。为此,本文在考虑视距(lineof-sight, LOS)和非视距(non-line-of-sight, NLOS)场景下,对LLSE、FPE 和WCE 的定位算法的特性(包括定位精度和算法的复杂度)进行分析计算。
1 基于UWB 的定位模型
图1 为基于UWB 的室内定位模型。将锚节点(reference node, RN)部署在已知坐标值的固定位置上,测量RN 的信号到达盲节点(blind node, BN)的时间(time of arrival, TOA),并用测距方程将TOA 转化为距离。然后将距离信息作为定位算法(LLSE、FPE 和WCE)的输入,最终得到盲节点位置的估计值。

图1 基于UWB 的定位模型
2 定位算法
2.1 线性最小均方误差估计(LLSE)算法
LLSE 属于UWB 室内定位算法中最简单的1 种。通过最小化观测数据间的均方误差[11]来估计节点位置。令 di为盲节点离第i 个锚节点间的距离[12],其定义为

式中: p =( xp,yp)为标签位置;pi=( xi,yi)为第i 个锚节点位置。对式(1)进行平方、简化处理后可得
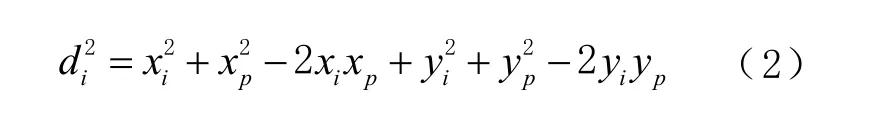
若有N 个锚节点,即 i =1, 2,… , N,可建立N 个等式。例如,第N 个等式为
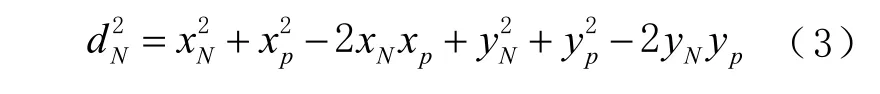
将式(2)与式(3)相减可得

将N-1 个等式减去第N 个等式,再以矩形形式表述为

式中:b 为( N- 1) ×1维矩阵; p 为 2 ×1维矩阵;A为(N- 1)×2 维矩阵,它们的定义为


若A 不是方矩阵,就利用伪逆矩阵估计节点位置[13]为

2.2 加权质心估计(WCE)算法
WCE 的算法先估计盲节点到锚节点的距离d,再依据这些锚节点位置和距离估计盲节点位置。
具体而言,令( x1,y1),( x2, y2),…,( xN, yN)表示这N 个锚节点的位置,1d , d2,…,dN表示这些锚节点离盲节点的距离,则盲节点的位置坐标(x,y)为
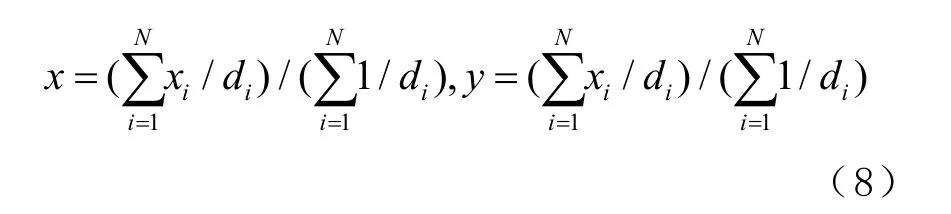
式中:i 表示锚节点的索引号;ix 表示第i 个锚节点的横坐标;yi表示第i 个锚节点的纵坐标。
盲节点根据距离远近选出与其最近的4 个锚节点,再利用这4 个锚节点位置即可出估计盲节点的位置。
2.3 指纹估计(FPE)算法
FPE 算法是基于UWB 测距的室内定位最常用的算法。先构建锚节点与盲节点间距离的指纹匹配图,然后计算当前距离,进而估计盲节点的位置。
具体而言,FPE 算法可分为离线采集和在线匹配2 个阶段,如图2 所示。

图2 指纹估计模型
在离线采集阶段,部署锚节点,并获取锚节点在各点位置的TOA 值,即将每个位置坐标信息和相应的TOA 值构成1 条信息链,形成1 条指纹。在在线匹配阶段,估计盲节点所接收的TOA 值,再与数据库里的指纹进行匹配,找到匹配度最高的位置作为盲节点位置。
令 fj表示存储在数据库的距离测量值,其定义为

式中M 为测量次数。
假定盲节点离锚节点的距离矢量为

再将 fj与d 进行比较,并将具有最小距离的位置点作为盲节点位置,即
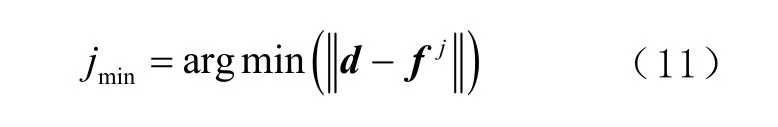
盲节点位置的估计值为

3 性能分析
为了更好地分析LLSE、WCE 和FPE 算法的性能,利用矩阵实验室(MATLAB)R2016a 软件建立仿真平台。考虑LOS 和NLOS 2 个场景。在2 维 100 m× 120 m 仿真区域内部署5 个锚节点和10 个盲节点,且以随机方式部署这些盲节点。10 个盲节点的真实位置如表1 所示。

表1 10 个盲节点的真实位置
先利用图1 流程建立模型测距,再利用LLSE、WCE 和FPE 算法估计盲节点位置。此外,在以下仿真图中:实黑圆点表示锚节点位置;三角形表示盲节点的真实位置;空心圆点表示算法估计的盲节点位置。
3.1 LOS 场景

图3 LLSE 算法对盲节点的位置估计(LOS 场景)

图4 WCE 算法对盲节点的位置估计(LOS 场景)

图5 FPE 算法对盲节点的位置估计(LOS 场景)
图3 ~图5 分别显示了LLSE、WCE 和FPE 算法对盲节点的位置估计,图中的横、纵坐标分别表示2 维区域长和宽。
从图3~图5 可知:相比于LLSE 和WCE,FPE算法能够准确估计盲节点的位置;LLSE 算法的估计误差最大;FPE 算法的均方误差为0.657 4 m;LLSE 算法和WCE 算法的均方误差分别为0.871 2 和0.723 4 m。
表2 为3 种算法的定位精度及复杂度程度。从表2 可以看出,FPE 算法的运行时间最多,这也说明FPE 算法的复杂度高,是以高的复杂度换取高的定位精度。

表2 LLSE、WCE 和FPE 算法的定位及复杂度性能(LOS 场景)
3.2 NLOS 场景
本小节分析3 个定位算法在NLOS 场景中的定位特性。图6~图8 显示了LLSE、WCE 和FPE算法的定位特性。
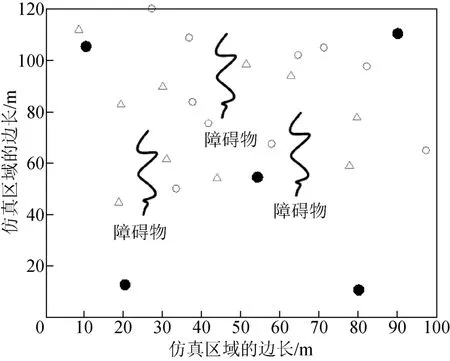
图6 LLSE 算法对盲节点的位置估计(NLOS 场景)

图7 WCE 算法对盲节点的位置估计(NLOS 场景)
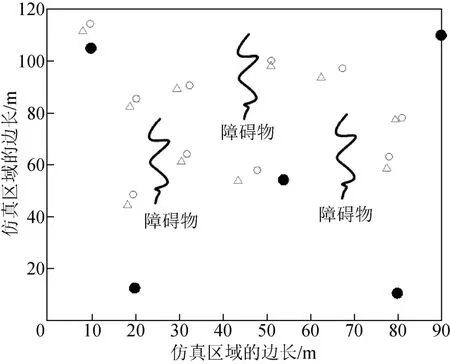
图8 FPE 算法对盲节点的位置估计(NLOS 场景)
正如预期的那样,相比于LOS 场景,NLOS 场景下的定位精度下降。原因在于:NLOS 场景中的障碍物阻碍了信号传输,扰动了对信号的TOA 测量,加大了测距误差,最终降低了定位精度。此外,相比于LLSE 和WCE 算法,FPE 算法仍具有高的定位精度。
表3 表示了3 个算法在NLOS 场景下的定位精度及运算时间。对比表2 和表3 内数据可知,NLOS 场景下的定位误差较差,例如,LLSE 算法在LOS 场景下的均方误差为0.871 2 m,而在NLOS 场景下的均方误差达到1.230 3 m。但各算法在LOS 和NLOS 2 个场景下运算时间并没有多大变化。
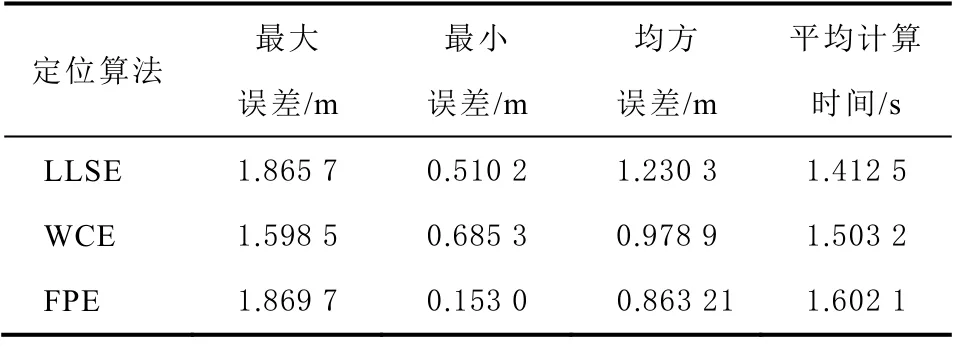
表3 LLSE、WCE 和FPE 算法的定位及复杂度特性(LOS 场景)
4 结束语
本文针对基于UWB 测距的室内定位算法进行分析,分析了在NLOS 和LOS 2 个场景下,LLSE、WCE 和FPE 算法的均方误差和复杂度。实验数据表明,相比于LLSE 和WCE,FPE 算法具有更低的定位误差,但复杂度较高。此外,NLOS 场景对定位有负面影响。相比于LOS 场景,NLOS 场景下的定位精度有所下降。

