WSNs 中基于凝聚法的信宿移动路径规划

王 梅，缪相林，张 媛，丁 凰

（1.西安交通大学 城市学院，西安 710018；2.西安交通大学 计算机学院，西安 710049）

0 引言

随着电子通信技术的快速发展，无线传感网络（wireless sensor networks, WSNs）[1]已在多个领域使用，如智慧农业、海洋环境勘察等领域。WSNs是由微型的、具有感知、通信、数据处理的传感节点组成。每个节点感测环境数据，再将数据传输至信宿或控制中心。最终，由信宿或控制中心对数据进行分析处理，进而实现对环境的监测。

不失一般性，这些微型传感节点由电池供电。因此，如何提高节点能量效率，进而使节点工作的时间更长，成为WSNs 的研究热点之一。由于节点须以多跳方式向信宿传输数据，传输数据消耗了节点的大部分能量。而位于信宿附近的节点，须多次协作转发其他节点的数据，它们的能量消耗速度更快，这就形成热点问题[2-3]。

热点问题阻碍了信宿的数据收集。因此，平衡网络内节点的能耗[4]，进而提高数据收集效率是十分有必要的。为了缓解热点问题，采用了移动信宿[5-7]（mobile sink, MS）概念，如移动机器人、无人机（unmanned aerial vehicle, UAV）。MS 通过遍历 WSNs 内每个节点，能够直接收集节点数据。

然而，遍历网络内每个节点是非常耗时的。为了减少遍历时间，MS 只遍历网络内部分点，这些点称为驻留点（rendezvous point, RP）[8-11]。这些RP 可能是网络内的节点或者网络区域内位置。多数文献是将RP 看成节点。

然而，将RP 看成区域内位置存在优势。图1描述1 个网络示例。

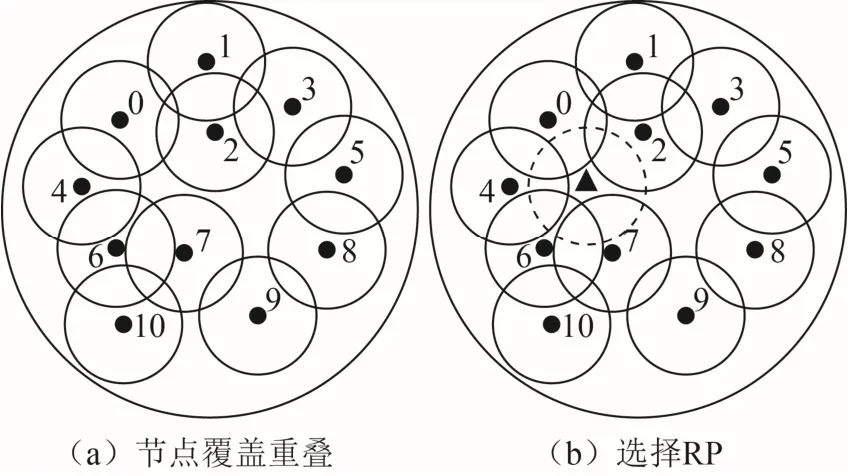
图1 RP 的选择（示例）

图1 （a）中，由于节点0、1、2、3、6 或7的覆盖区域与其他的3 个节点重叠，它们很可能被选为RP。而若考虑位置作为RP，如图1（b）所示，将三角形位置作为RP，则RP 能够直接与多个节点通信。

有效地选择RP 能够均衡网络能耗，控制拥塞，进而提高网络寿命[3]。为此，本文针对3 维WSNs，提出基于层次聚类法的数据收集（hierarchical agglomerative-based data collecting, HADC）算法。先利用层次聚类将节点划分不同簇，并利用层次聚类得到最优的簇数，再将每个簇的中心位置作为RP。MS 就沿着RP 移动，进而收集网络内数据。

1 系统模型

n 个 节 点 随 机 分 布 于 ℓ · ℓ ·ℓ 立 体 区 域 内，用S= {s1, s2, s3,… , sn}表 示 这 n 个 节 点 集， 用Pi= ( xi, yi,zi)表示 si节点的位置。

用M 表示RP 集。MS 依据RP 移动，并收集数据。如图2 所示，假定MS 在遍历每个RP 所消耗的时间足够用于数据的收集，信宿知晓网络内所有节点的位置，并假定MS 有足够的存储空间和能量收集数据，且在MS 的移动路径中无障碍。

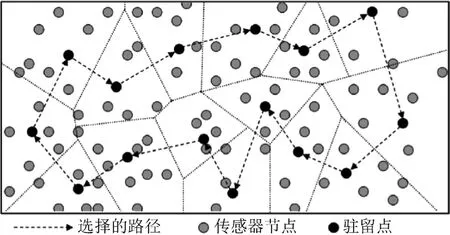
图2 基于RP 的MS 收集数据过程

2 HADC 算法

2.1 基于层次聚类的簇

层次聚类算法属于无监督的机器学习算法，有2 种策略：自底向上的凝聚法和自上向下的分裂法。凝聚法是指许多基于相同原则构建的聚类算法；分裂法是将初始样本归成1 个簇，再依据具体准则逐步分裂，直至满足预设的条件，才终止分裂。

凝聚法将初始样本看作1 个类簇，再依据具体准则合并这些类簇，直到满足预设的条件，才终止。HADC 算法引用凝聚法，并利用2 个簇间的最小距离作为合并的依据。

对于2 个簇 cx和 cy，它们的距离等于这2 个簇内节点间的最小距离值，即

式中： si∈ cx； sj∈ cy。

凝聚法最初并不设定所需的簇数，而是通过对簇进行迭代，直到每个节点都归属1 个唯一的簇。图3 给出了执行凝聚法过程。

图3 执行凝聚法过程

从图3 可知：凝聚法先假定每个节点作为1 个簇，即n 个节点形成n 个簇；依据式（1）寻找相距最近的簇，并将它们合并成1 个簇；再依据式（1）迭代，直至满足条件。这就形成基于簇的树结构，将其称为凝聚簇树的层次结构。

2.2 RP 的选择

依据算法1，可得到λ 级簇类层次拓扑结构，且 n ≥ λ≥ 1。每1 层包含k 个簇，即 Cλ= {G1, G2,… ,Gj,… , Gk}，其中Gj表示第j 个簇。且用 nj表示Gj簇内的节点数。

优化λ 值，选择最优的RP，进而能够提高数据收集效率，降低能耗。据此，需要采用优化算法决策λ 值。HADC 算法采用统计算法估计最优的λ 值。

具体而言，先计算每个簇的质心位置CP。令CPj表示Gj簇的质心位置，其定义为

对于单个的Gj簇，将簇内所有节点离簇质心CPj的距离的平均值作为簇的权重，即

式中 d (CPj, Pi)为Gj簇内节点 Pi∈ Gj离CPj的距离。

簇内权重（inter-cluster weight, ICW）等于簇权重的均值，即簇Gj的ICW 为

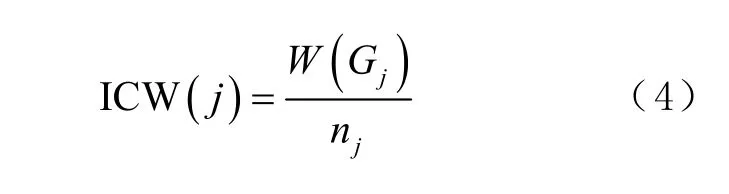
用簇间距离（intra-cluster distance, ICD）表述2 个簇间的距离，簇Gj的 ICD ( j )等于在同一层中所有簇离自己的最小距离，其定义为

引入簇的紧凑-分离率（compact-separate proportion, CSP）变量，其定义为

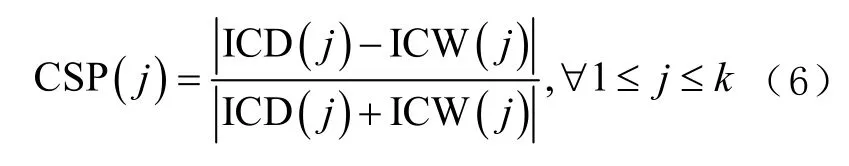
并计算在iλ 层的k 个簇的CSP 的平均值

依据 A_CSP ( k )计算在每一层λ 的最优簇数，即 kopt为

3 实验与结果分析

3.1 仿真环境

通过派森（Python）软件构建仿真平台，分析HADC 算法的性能。在100 m × 1 00 m × 1 00 m 的区域部署 100～400 个节点。sink 的移动速度为ϑ= 0.5m/s ，具体的仿真参数如表1 所示。

表1 仿真参数

为了更好地分析HADC 算法的性能，选择文献[9]提出的权重驻留点规划（weight rendezvous planning, WRP）算法、文献[10]提出的移动信宿的有效数据收集（efficient data gathering with mobile sink, EDGS）算法和文献[12]提出的基于层次簇的驻留点的数据收集（hierarchical clusteringbased determine rendezvous data gathering, HCRG）算法作为参照，并分析它们的能耗、网络寿命的性能。

3.2 平均能耗

将MS 在遍历1 轮时，网络内所有节点的能耗平均值作为平均能耗，其定义为

式中：n 为传感节点数；iE 为节点is 所消耗的能量。

图4 显示了HADC 算法、WRP、EDGS 和HCRG 算法的平均能耗随节点数的变化情况。

由图4 可知，平均能耗随节点的增加而呈上升关系。原因在于：节点数的越多，所产生的数据包数越多，节点需要转发的数据包数也越多，这必然增加节点能耗。

图4 不同算法的平均能耗

相比于WRP、EDGS 和HCRG 算法，本文提出的HADC 算法的平均能耗得到有效的控制。与WRP 算法相比，HADC 算法的能耗下降约46%。这要归结于HADC 算法通过优化簇，并利用簇内质心位置作为RP 位置，进而优化了RP 集。

3.3 网络寿命

本次实验分析HADC 算法的网络寿命，将MS从网络开始至网络内第1 个节点的能耗殆尽所遍历的轮数作为网络寿命。图5 显示了HADC 算法的网络寿命随节点数的变化情况。

图5 网络寿命

从图5 可知，节点数的增加，降低了网络寿命，这与图4 的能耗数据匹配。能耗的增加，加速了节点能耗速度，使出现能耗殆尽节点的时间提前。

相比于WRP、EDGS 和HCGR 算法，HADC算法的网络寿命得到有效提高。相比WRP、EDGS和HCGR 算法，HADC 算法的第一能量消耗殆尽节点出现的轮数分别推迟了约1 446、1 109 和1 069 轮。

3.4 能耗均衡

引用公平指标（fairness index）表征网络节点间的能耗均衡性能，其定义为

式中：eβ 表示传感节点的能耗的标准差； Em、uE分别表示最大的能耗和最小能耗。eβ 值越大，公平指标F 值越低。

图6 显示了WRP、EDGS、HCGR 算法和HADC算法的公平指标随运行轮数的变化情况。

图6 能耗均衡的公平指标

从图6 可知，HADC 算法的F 值接近1。即使运行150 轮后，HADC 算法的F 值也达到0.97。相比之下WRP、EDGS、HCGR 算法的F 值随运行轮数的增加，快速下降，当运行150 轮后，它们的F 值低至0.5。

4 结束语

针对3 维的WSN 网络，提出基于层次聚类法的数据收集HADC 算法。HADC 算法通过信宿的移动收集数据，进而平衡网络内节点间的能耗。先利用层次凝聚法产生簇，并从能耗角度优化簇个数，再将每个簇内的质心位置作为驻留点，进而产生驻留点集。这些驻留点就构建了移动信宿的移动路径。仿真结果表明，提出的HADC 算法有效地减少了能耗，并均衡了能耗的平衡性。