单位根左侧调整Wald联合检验量研究

王晓强 江海峰

（安徽工业大学 商学院，安徽 马鞍山 243032）

0 引言

众所周知，单位根检验是检验经济理论、防止伪回归、深入研究其他相关理论不可缺少的环节。因此，检验宏观经济时间序列是否为单位根过程，一直成为理论和实证研究的热点。自单位根DF检验提出以来，单位根检验量理论不断深入发展。在检验量改进研究方面，学者们先后提出ADF检验、PP检验、KPSS检验、ERS检验和NP检验，这些检验方法被计量经济学软件所采纳，成为目前单位根主流检验方法[1-6]。在检验方法改进方面，不少学者将Bootstrap方法引入到单位根检验中，取到了较好的检验效果[7]。Phillips和Magdalinos[8]在单位根检验引入相关变量从而提出IVX检验方法，Hepsag[9]考察结构突变非线性调整单位根检验方法。在检验时间序列频率方面，Hylleberg等[10]考察季节数据，提出季节单位根HEGY检验，而Laurent和Shi[11]进一步提出高频数据单位根检验方法。其他相关研究不一而足，这里不再赘述。

由于单位根检验结论同时受到数据生成过程和检验模型设置影响，从某种程度上说，单位根检验过程就是确定数据生成过程。为此，Doldado等[12]、江海峰和汪忠志[13]分别提出单位根DJSR检验流程和KPSS检验流程。就DJSR检验流程来说，单位根检验不仅要检验单位根项，还需要同时考察与漂移项和趋势项的联合检验。聂巧平和张晓峒[14]、张凌翔和张晓峒[15-16]分别考察DF类单位根中联合检验的F检验量、Wald检验量和LM检验量。左秀霞[17]进一步考虑单位根检验中高次趋势联合F检验量分布。和其他检验量一样，这三类检验量仅考察原假设成立时信息，在检验量构建过程中采用双侧假设检验模式，而忽略了备择假设中单侧设置形式所提供的信息。Abadir等[18]研究表明，融入备择假设信息的联合检验量能够提高检验功效。由于单位根检验属于单边左侧检验，因而可以尝试将单侧检验信息融入到上述联合检验量构造中。鉴于F检验量、Wald检验量和LM检验量的相似性，文章以Wald检验量为代表展开研究。首先，按照数据生成过程是否包括漂移项，分类讨论单位根检验中左侧联合检验量的构建；其次，研究大样本下调整联合检验量的分布，利用蒙特卡洛模拟技术获取左侧调整联合检验量分位数；最后，从分位数、检验水平和检验功效三个角度和无调整联合检验量进行比较。这些研究完善了单位根检验流程理论，为实证研究提供一种新检验方法。

1 单边检验量构造

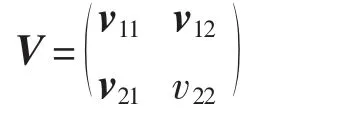
根据经典Wald检验量构造有

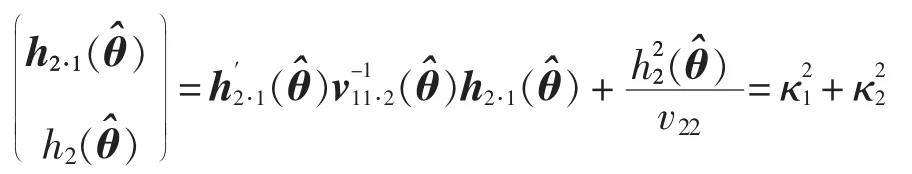
其中I（·）为示性函数，条件成立取1，否则取0。

2 单位根检验左侧联合检验量构建研究

2.1 无漂移项单位根数据生成过程

不失一般性，为便于叙述，文章研究DF模式下的左侧调整联合检验量构建，对于PP检验和ADF检验也可以类似研究。沿用文献[15]中的记号，与W22、W33检验量对应的数据生成过程为

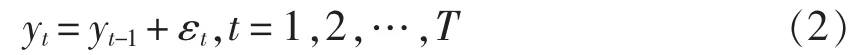
其中 εt～iid（0，σ2），y0=0，T 为样本容量。估计模型分别为

在模型（3）中检验 H01∶α1=0，ρ1=0，在模型（4）中检验 H02∶α2=0，δ1=0，ρ2=0，检验量分别记为W22、W33。设 diag（·）表示以括号内元素构造对角阵，W（·）表示定义在[0，1]内的布朗运动。引入相关记号如下

对检验 H01∶α1=0，ρ1=0、H02∶α2=0，δ1=0，ρ2=0 有h11（θ1） = α1，h12（θ1） = ρ1，，h22（θ2） = ρ2对模型（3）令

记左侧调整Wald联合检验量分别为W22adj和W33adj，⇒表示弱收敛，则有以下定理1成立。

定理1 设数据生成为式（2），分别估计模型（3）和模型（4），检验假设 H01∶α1=0，ρ1=0、H02∶α2=0，δ1=0，ρ2=0。记左侧调整 Wald联合检验量为 W22adj和 W33adj，则有

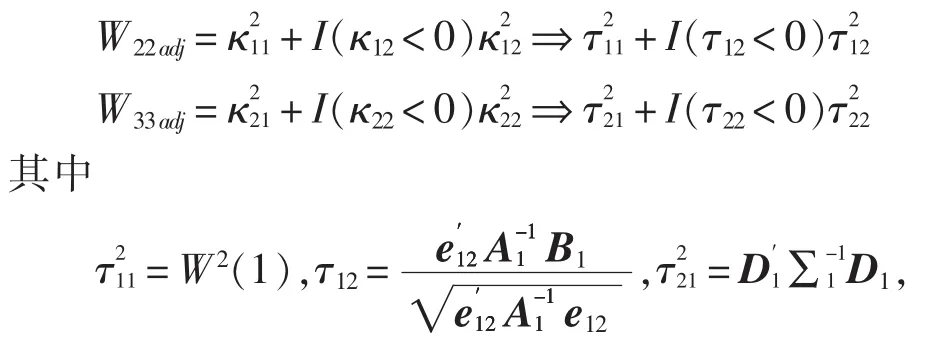
证明 由OLS估计知，模型（3）和模型（4）的参数估计量及其方差在大样本下服从分布为

纵观马克思的青年时代，他也拥有本属于青年人的一般特质，甚至曾经是一个叛逆青年。他曾经流连于所谓“特里尔同乡会”组织的各种聚会当中，也曾因为每个月的巨额花销遭到父亲的斥责。但是，这些只是一个年轻人在成长过程中的一段插曲，而马克思在青年时代所展现出的与众不同的精神特质，注定意味着他将在自己的人生中谱写出壮丽的乐章。

i=1，2。对模型（3），根据式（5）计算表明

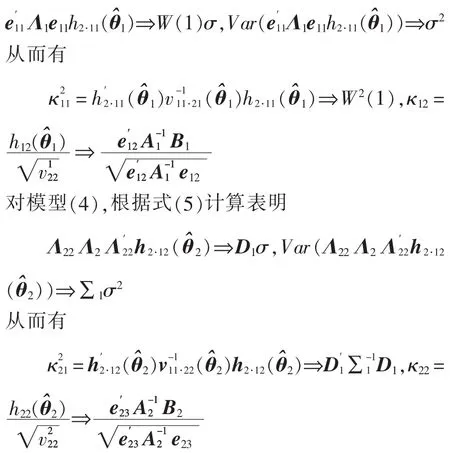
带入W22adj和W33adj表达式，且示性函数I（·）为连续函数，根据连续映射定理，容易验证定理1成立。

2.2 有漂移项单位根数据生成过程

设数据生成过程为

此时估计模型分别为模型（7）和模型（8）

在模型（7）中建立假设 H03∶α3=c，ρ3=0，在模型（8）分别建立假设 H04∶δ2=0，ρ4=0，H05∶α4=c，ρ4=0，H06∶α4=c，δ2=0，ρ4=0。对模型（8）进行共线性处理得

证明 对模型（7）而言，当数据生成为式（6）时，参数估计量及其方差分布在大样本下有

带入检验量W32adj的表达式可得结论成立。类似可证明W34adj、W33adj的分布也成立，从而定理2成立。

3 仿真模拟研究

和无调整Wald联合检验量一样，调整Wald联合检验量在大样本下收敛到维纳过程的泛函，也为非标准分布，但与无调整Wald联合检验量分布不同。为此，需要使用蒙特卡洛模拟技术获取分位数，所有仿真模拟采用统计软件SAS9.4。设置模拟次数为50万次，扰动项εt服从标准正态分布。不失一般性，令漂移项c=0.1。为进行对比，同时列出无调整和调整的Wald联合检验量分位数。限于篇幅，这里只列出95%分位数，结果如表1所示。表1给出了13种样本下的95%分位数模拟结果。表1反映出3条结论。第一，随着样本容量的增大，各个检验量的分位数呈现下降趋势，但降幅趋缓，这与各个检验量在大样本下具有明确的分布相吻合。第二，固定样本容量时，所有调整Wald联合检验量的分位数都小于对应无调整Wald联合检验量的分位数。第三，联合检验量W22adj与W22、Wadj与W分位数差异相对较大，其他三组调整联合检验量，与对应的无调整联合检验量分位数相差很小，个别场合在小数点后三位完全相同。原因是模型（3）、模型（7）中1＜ 0 和3＜ 0出现的机会比模型（4）、模型（9）中2＜ 0 和4＜ 0出现的机会要小，机会越小，调整Wald联合检验量与无调整Wald联合检验量分位数相差越大。下面表2给出与表1相对应单位根项估计小于零出现的比例。显然，1＜0出现机会基本在95%左右，2＜0 与4＜ 0 出现机会高达 99%，而3＜ 0出现机会最小，且随着样本增大呈现下降趋势。

接下来考察检验水平和检验功效，设置模拟次数为1万次，其他设置与分位数模拟设置相同。取单位根项 ρ分别为 1.00、0.95、0.90、0.85 和0.80。其中，取值为1.00表示单位根数据生成过程，对应检验水平；其他4组值表示数据生成为平稳过程，对应检验功效。表3给出了部分样本下模拟结果，分位数来自表1。就检验水平而言，考虑到抽样的随机性，当取显著性水平为5%时，计算表明，名义检验水平区间估计为[4.57%，5.43%][19]。表3显示，当ρ取值为1.00时，所有检验量检验水平基本以5%为中心作上下波动，且落在上述区间估计内，表明左侧调整Wald联合检验量也具有满意的检验水平。当ρ取值小于1考察检验功效时，表3揭示出3点结论。第一，固定样本容量时，检验功效随ρ降低而增大。以调整联合检验量W22adj为例，当样本容量为25时，ρ分别取0.95、0.90、0.85和0.80时，检验功效分别为4.10%、4.38%、5.66%、7.894%，递增趋势明显。第二，固定ρ取值时，检验功效随着样本容量增大而增大。仍以调整联合检验量W22adj为例，ρ取0.95，6种样本下检验功效分别为 4.10%、5.04%、7.70%、22.42%、34.92%和92.75%，增幅也显著。第三，所有左侧调整Wald联合检验量检验功效，都不低于对应的非调整联合检验量检验功效，尤其是联合检验量W22与W22adj、W与Wadj，左侧调整Wald联合检验量检验功效优势明显，只有当样本足够大，或者ρ与1.00偏离较大时，此时两类检验量检验功效近乎相等。联合检验量 W33与W33adj、W32与 W32adj、W34与W34adj的检验功效基本相当，在少数场合，左侧调整Wald联合检验量功效略高于无调整Wald联合检验量检验功效。检验功效模拟研究表明，左侧调整Wald联合检验量具有明显的功效优势，功效差异程度取决于单位根项估计值小于零的比例，比例越大，功效差异越小，因此表3反映的功效差异与表2给出的比例差异相吻合。

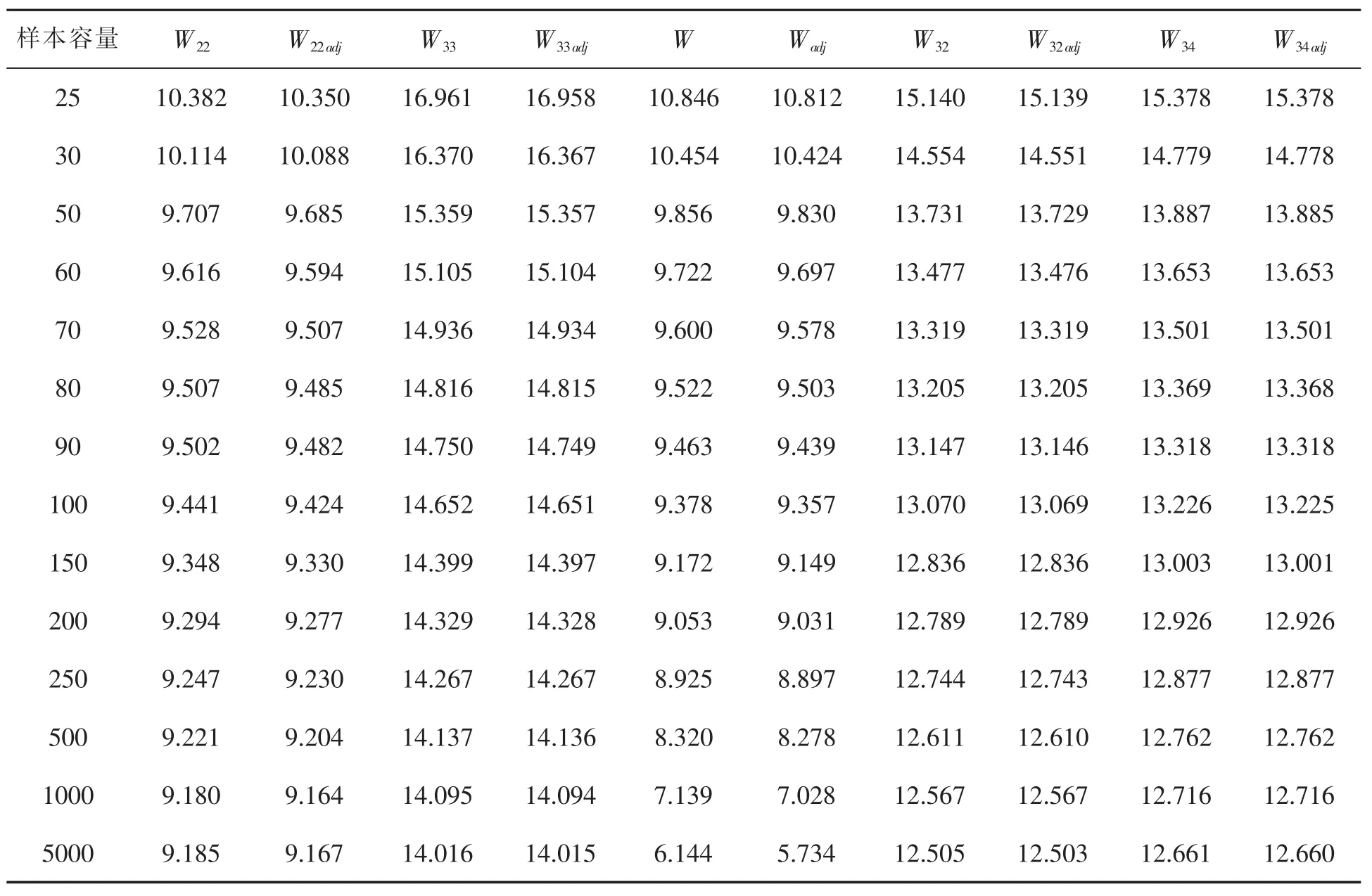
表1 两种数据生成过程下无调整和调整Wald联合检验量95%分位点模拟值

表2 两种数据生成过程下单位根项小于零出现的比例（%）

表3 两种数据生成过程下无调整和调整联合检验量检验水平与检验功效（%）

4 结论与建议

文章以单位根过程Wald联合检验量为研究对象，按照数据生成过程是否含有漂移项，分别引入左侧调整模式，构造左侧调整Wald联合检验量，得到以下几点结论。

（1）理论研究表明，和无调整Wald联合检验量一样，在大样本下，左侧调整Wald联合检验量分布收敛到维纳过程的泛函，但与无调整Wald联合检验量分布不同，因此需要重新模拟分位数。

（2）分位数模拟显示，当样本容量相同时，左侧调整Wald联合检验量分位数不超过非调整Wald联合检验量分位数，两者之间的差异取决于单位根项小于零的比例，比例越大，分位数差异越小。

（3）就检验水平而言，当使用名义检验水平95%置信区间估计结果考察检验水平时，左侧调整Wald联合检验量与无调整Wald联合检验量都具有满意的检验水平。因此，从检验水平角度来说，左侧调整Wald联合检验量没有出现过渡拒绝和拒绝不足原假设情况。

（4）就检验功效而言，左侧调整Wald联合检验量的检验功效不但继承无调整Wald联合检验量检验功效所具有的特征，而且具有明显的功效优势，功效差异程度与单位根项估计值小于零的比例有关。

文章在理论上改进单位根联合检验方法，完善单位根检验流程，实践上也为实证研究提供一种新检验方法。结合理论和模拟分析结果，提出三点建议。第一，在实证研究中，可以同时使用经典Wald联合检验量和左侧调整Wald联合检验量，但以后者结论为准。第二，为进一步考察单边调整的优势，可以继续研究左侧调整LM联合检验量和F检验量的检验效果，并与左侧调整Wald联合检验量进行对比。第三，随着泡沫检验理论兴起，可以在泡沫检验中引入右侧调整Wald联合检验量，进一步完善资产价格泡沫计量模型检验理论。