二分法解非线性方程的算法设计和Matlab程序
杨柳玉 宋东翔 杨世玲
(德宏师范高等专科学校,德宏 678400)
一、引言
在科学研究和科学计算中常常碰到非线性方程求解问题。非线性方程的解一般不能解析求出。所以数值解法显得非常重要,而数值解法在实际中的实现则更为重要,下面介绍二分法解非线性方程在Matlab 里的实现程序[1]。
二、二分法
二分法又称对分区间法,是求f(x) = 0 根的一种简单直观方法。函数f(x) 在闭区间连续,且f(a)f(b) < 0 则f(x)= 0在(a,b) 内必有实根,此为微积分中的零点定理。然后取由零点定理确定f(x)= 0在[a,c]与[c,b]是否有实根,确定有根区间后取有根区间中点继续重复做,可得近似根。可见微积分中的零点定理是使用二分法的前提[2]。
设函数f(x)在区间[a,b]连续,假定f(a) <0f(b) >0 取中点,检查f(x0)的符号。若f(x0) =0,则x0就是一个根; 若f(x0) >0,记a为a1,x0为b1,则得有根区间[a1,b1];若f(x0) <0,记x0为a1,b为b1,则得有根区间[a1,b1]。后两种情况都得到有根区间[a1,b1],它的长度为原区间的一半。对[a1,b1],令x0=a1+b1,再施以同样的方法,可得新的有根区间[a2,b2],它的长度为[a1,b1]的一半,如此反复进行下去,其中每一个区间是前一区间的一半。有这就是方程的根。而即为方程的近似根,且有估计误差[3][4]。
三、二分法的算法设计
(一)二分法的计算步骤
1.求有根区间[a,b]。有两种方法,下面会举例列出。
2.根的精确化。即已知一个根的近似值,逐步提高根的精度,直到满足所要求的精度为止。
(1)输入起点a,步长h,方程f(x),误差e
(2)计算b=a+h
(3)当f(a)f(b) >0时,做
a=a+h
b=a+h
若f(a)f(x) <0 则 ;b=x
若f(a)f(x)==0x=x;
若f(a)f(x)>0a=x;
(7)输出x
四、Matlab 程序和计算实例
例1用二分法求非线性方程f(x)=x3-x- 1 =0在区间(1,2)内的一个实根。
分析:先求出有根区间(法一);
当精度控制量 e=0.001 时,求出根的近似值。
解:
(1)先求出有根区间
因为二分法只能求单根,首先可以搜索函数 在f(x) =x3-x- 1 = 0 、在MATLAB 命令窗口输入如下命令:
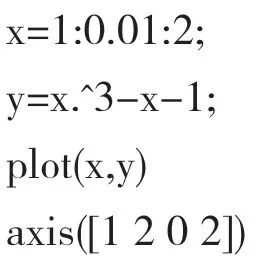
从图一可以看出f(x)=x3-x- 1 =0在区间(1,2)内有惟一的一个大于1.3 而小于1.4 的单根。
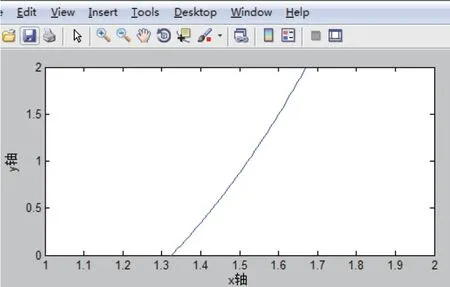
图一 在区间 上的图像
(2)Matlab 程序实现:
先建立ey.m
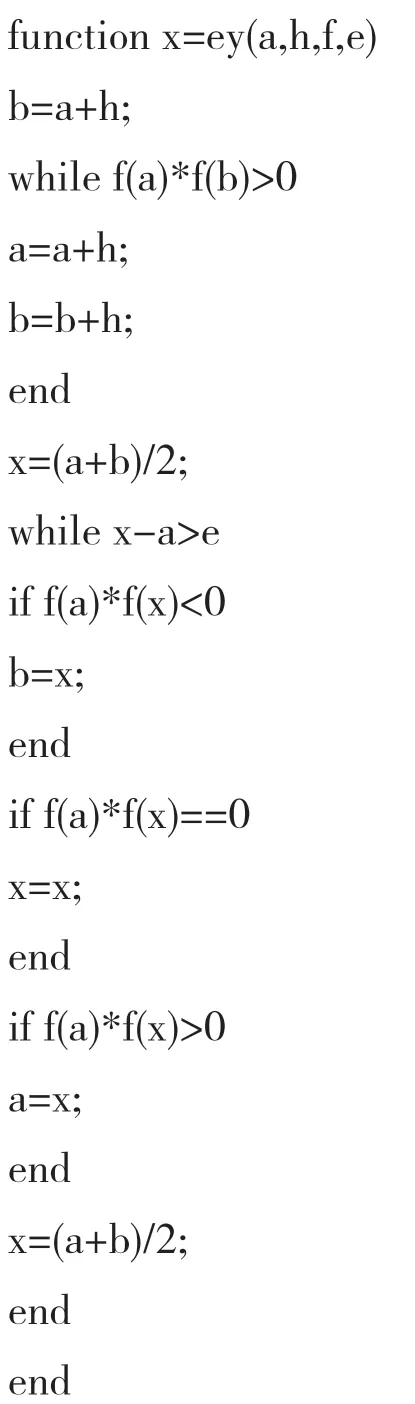
(3)最后在MATLAB 命令窗中输入:

例2:下面用二分法求非线性方程f(x)=x3- 5 =0的一个实根。
解:
(1)先求出有根区间(法二)
取扫描起点a=1,h=0.1,寻找有根区间如下表所示:

k 0 1 2 3 4 5 6 7 a 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 k b a h 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8= +kk f a f b符号() ()+++++++-k k
故f(x)=x3- 5 =0在区间(1,2)内的有根区间是[1.7,1.8]。
用二分法求近似值,计算结果如下表所示:
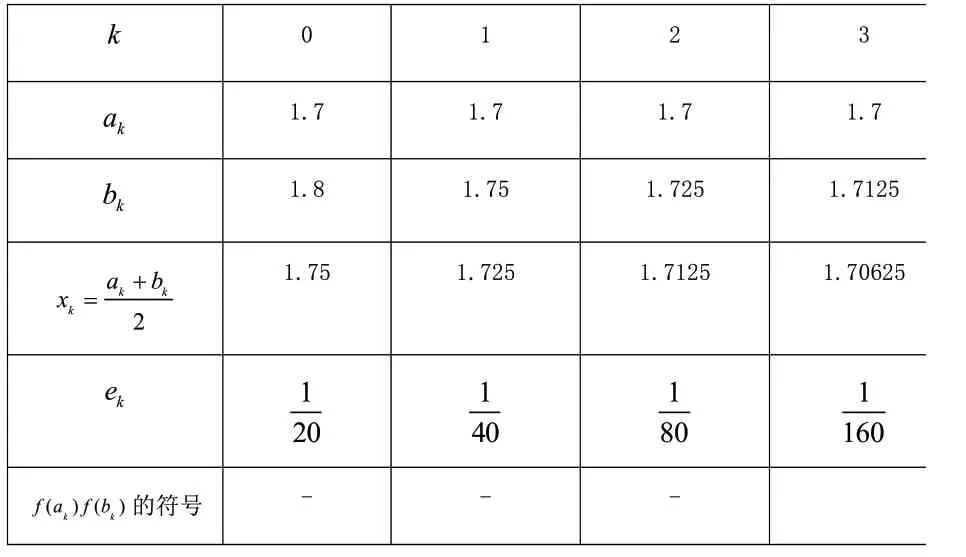
k 3 0 1 a 1.7 1.7 1.7 1.7 kb 1.8 1.75 1.725 1.7125 k 1.75 1.725 1.7125 1.70625 k a b x=kk +e 2 1 k 1 40 1 80 1 20 160 k f a f b 的符号---k () ()2
故当k=3时,,近似解取为x3=1.70625 。
(3)Matlab 程序实现:
先建立eff.m


五、结束语
二分法是求非线性方程近似根的最简单的方法,它的数学思想推行过程简单易行,便于在计算机上实现。本文结合两个非线性方程介绍了二分法解非线性方程的算法设计和Matlab程序。

