定性确证理论的相干性难题及出路
段天龙,顿新国
(南京大学 哲学系, 江苏 南京 210023)

重新考察定性确证标准所刻画的确证模式的基本特征及其面临的各种相干性难题,不仅有助于准确把握定性确证理论研究的转向和发展态势,也有助于发现需要进一步研究的问题,从而推动定性确证理论的发展。
一、定性确证理论的两个代表性路径
在构建定性确证标准时,我们会面对这样的问题:该如何在形如“Aa∧Ba”的数据陈述和形如“∀x(Ax→Bx)”的假说陈述之间建立逻辑句法关系,从而逻辑而非历史地说明相应数据和假说之间应该具有的确证关系呢?在经典逻辑推理规则下,公式“Aa∧Ba”和“∀x(Ax→Bx)”之间既不满足∀x(Ax→Bx)├Aa∧Ba,也不满足Aa∧Ba├∀x(Ax→Bx)。也就是说,基于经典逻辑,形如“Aa∧Ba”的证据和形如“∀x(Ax→Bx)”的假说之间并没有直接的演绎关联。但幸运的是,存在两种基本的演绎模式可以将二者间接地关联起来:
Aa∧Ba确证∀x(Ax→Bx),因为:
(a)∀x(Ax→Bx)├Aa→Ba,且Aa∧(Aa→Ba)├Ba;
(b)∀x(Ax→Bx)├Aa→Ba,且Aa∧Ba├Aa→Ba。
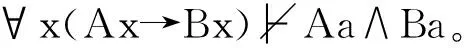

不难看出,在PC中,数据(集)不再是一个“整体”。说数据是一个整体是指——在一个衍推关系中,数据集中的所有数据要么都作为前提出现要么都作为结论出现。由于事例是一般性假说的个例,即在某种特定情况中对假说所表达内容的完整述说,所以只有保持数据集的整体性,才能形式地表达事例概念。与模式(a)相比,模式(b)中的数据集显然是一个整体,这也是亨佩尔(Carl Gustav Hempel)提出的作为事例确证理论之“满足性标准”(satisfaction criterion,即SC)的形式基础:
(SC)E确证H,当且仅当,E├dev(H,E)。(4)其中,dev(H,E)表示H在E上的展开。
之所以将SC称为满足性标准,是因为它的基本思想是“如果某假说在观察报告所提及的对象的有限类上被满足,那么该假说被给定观察报告所确证”(5)Carl G.Hempel,“Studies in the Logic of Confirmation”,Aspects of Scientific Explanation,New York:Free Press,1965,p.37.。PC和SC分别体现了H-D和事例确证的基本形式特征:(1)H-D所强调的是:如果数据集E中的某些数据能够和某个假说H一起衍推该数据集中的其他数据,那么H就解释了这些数据之间的某种演绎关系,即H解释了这些数据为何属于同一个数据集E。也是在这个意义上来说,H被E确证。所以,根据PC,“一只黑色的非乌鸦”不确证乌鸦假说,即数据“Ra∧Ba”不是假说“∀x(Rx→Bx)”的证据,因为“∀x(Rx→Bx)”无法解释数据Ra和数据Ba之间的演绎关系;(2)与H-D(实质上)强调假说对数据集的不同数据之间的演绎关系的解释不同,基于枚举归纳直觉——所谓的归纳推理方法通常被认为是从个例到一般性假说的过程,其中每个个例都是一个事例,事例确证更强调数据集作为一个整体和假说之间具有某种衍推关系。对此,亨佩尔使用“满足”(satisfy)描述E和H之间的确证关系,即如果某假说在观察报告所提及的对象的有限类上被满足,那么该假说被给定的观察报告所确证;相较之下,作为亨佩尔事例确证理论的发展者,格莱莫尔(Clark Glymour)使用“协调”(accord with)来描述E和H之间的确证关系,即“E确证H当且仅当E与H协调”。
二、定性确证理论遭遇的相干性问题
事例确证和H-D这两类定性确证标准,都很好地捕捉了理性主体关于证据性支持关系的直觉,但进一步分析表明它们各自面临一些相干性问题,克服这些问题成为定性确证理论发展的最大动因。这些相干性问题主要可分为两类:(i)句法相干性问题。如果某数据和某假说在语义上(或事实上)被认为具有证据性支持关系,但表述数据的陈述和表述假说的陈述却不满足给定的确证标准所要求的逻辑句法关系,那么就说该确证标准面临句法相干性问题,主要有“事例确证问题”(the problem of instance confirmation)和“超证据词汇问题”等;(ii)语义相干性问题。如果表述数据的陈述和表述假说的陈述之间满足给定的确证标准所要求的逻辑句法关系,但相应数据和假说在语义上(或事实上)被认为不具有证据性支持关系,那么就说该确证标准面临语义(或事实)相干性问题,主要有“缝合问题”(tacking problem)、“克里斯滕森(David Christensen)反例”和“乌鸦悖论”等。纵观定性确证理论发展史,刻画二元确证关系的确证标准通常会面临句法相干性问题,而刻画三元确证关系的确证标准虽然能够避免句法相干性问题却又会面临语义相干性问题。
(一)事例确证问题
所谓“事例确证问题”是指:直观上假说应该被其事例所确证,但相应的假说陈述和其事例陈述之间却不具有某确证标准所要求的演绎关系,那么就说该确证标准面临事例确证问题。作为一种句法相干性问题,该问题的提出主要是针对H-D的原初形式H-D0:E确证H,当且仅当,H├E且E是真的。可见,根据H-D0,形如“Aa∧Ba”的数据不能确证形如“∀x(Ax→Bx)”的假说。也就是说,“一只黑色乌鸦”不能成为乌鸦假说的证据,而这显然有悖于枚举归纳这一最简单的归纳推理直觉。
(二)超证据词汇问题
PC和SC都可以避免事例确证问题,因为既可以有Aa∧Ba├Aa→Ba也可以有Aa∧∀x(Ax→Bx)├Ba。然而,这两个确证标准都认为数据和假说之间的确证关系是二元的,而所有的二元确证关系都会(不同程度地)具有一个狭隘性缺陷——不允许对其词汇超出证据词汇的假说的确证。在科学中,假说词汇超出证据词汇的情形比比皆是。例如,牛顿万有引力定律所包含的词汇就比作为其证据的牛顿第二定律丰富。此时,无论是PC还是SC都不能说明二者之间的确证关系。为了便于论述,本文将这一状况称为“超证据词汇问题”。当然,对于PC来说,“H的基本词汇比E的基本词汇更广泛”的表述是不够精确的,它可以被细分为两种不同的情况:(1)Q(E)⊆Q(H);(2)Q(E)∧Q(H)≠Q(E)。其中,Q(X)表示语句X的基本词汇集。在第一种情况下,根据PC,E确证H,因为此时满足E1∧H├E2;在第二种情况下,根据PC,E不确证H,例如E为“Aa∧Ba”而H为“∀x(Cx→Dx)”,此时PC将面临和H-D0相似的困难。
(三)缝合问题
为了解决超证据词汇问题,假说-演绎主义者从不同角度对PC进行了修正。这些新的预测标准的差异主要体现在是否保留条件“E≡E1∧E2”。霍维奇(Paul Horwich)保留了这一形式要求:
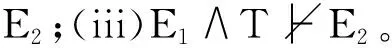
然而,PC*面临和PC相同的问题——“合取缝合问题”:对于任何语句H′,如果E相对于T确证H,那么H∧H′也被E相对于T确证。与霍维奇不同,梅里尔(Gary Merrill)放弃了条件“E≡E1∧E2”。如果说“E≡E1∧E2”是将数据E划分为子数据E1和E2,那么梅里尔则提出了“子假说”(sub-hypothesis)的概念:K是假说H的子假说当且仅当K是H的非等价的逻辑后承。进一步,K是假说H的真子假说,当且仅当K是H的非等价的逻辑后承,并且存在一个H的子假说L使得K和L的合取可以穷竭假说H。基于此,梅里尔提出了自己的预测标准:

直观地,条款(ii)要求假说中不存在非相干元素。因为,如果当H∧H′被替换为H∧H*后仍然被E相对于T确证的话,那么说明H′相对于E是非相干的。所以,基于子假说概念PCm避免了合取缝合问题。然而,由于该标准仍然基于H∧T├E这种基本形式,即E(简单地)出现在结论中从而致使H∧T├E∨E′也被满足,所以使其会面临另一种类型的缝合问题——“析取缝合问题”:对于任何语句E′,如果E相对于T确证H,那么H也被E∨E′相对于T确证。合取缝合问题和析取缝合问题也成为H-D面临的主要的相干性问题。
(四)克里斯滕森反例
与霍维奇和梅里尔不同,为了避免超证据词汇问题,格莱莫尔将亨佩尔事例确证理论发展为对三元确证关系的说明:
(SC*)E相对于T确证H,当且仅当,E∧T├dev(H,E)。(8)Clark Glymour,“Relevant Evidence”,The Journal of Philosophy,Vol.72,No.14,1975.
其中,E′是通过否定E的某些合取肢得到的。例如,如果E为Ra∧Ba,那么E′可以是Ra∧Ba或Ra∧Ba或Ra∧Ba。SC*+FC构成了格莱莫尔拔靴带条件(BS)的核心思想:H相对于T而被E所确证。条件是,我们能够使用T从E中推导出H的一个(肯定)事例,并且这一推导过程不确保无论我们已经具有什么E都将获得H的一个事例。不难看出,BS不仅可以避免句法相干性问题也能避免已知的缝合问题,因为和SC一样,在BS确证模式中H和E分别出现在结论和前提中,而基于经典逻辑的性质,对结论合取和对前提析取都将导致推理无效。
尽管BS可以避免上述难题,但它不仅没有解决乌鸦悖论,而且会遭遇新的语义相干性问题——“克里斯滕森反例”。所谓克里斯滕森反例是克里斯滕森针对BS提出的一组反例,这组反例之所以成立是因为:格莱莫尔认为数据、假说和理论构成的系统是演绎封闭的,这将导致给定任意的假说H和理论T我们都可以得到逻辑后承“H↔T”,而H和T可以是语义非相干的任何语句。结合其他语义相干性问题不难发现,之所以会出现这种非相干的关联是因为:现有的确证标准都是基于经典逻辑的,但经典逻辑所关注的是后承关系的有效性并非相干性。所以,为了避免有效但非相干的推理,科学哲学家从对数据和假说之间演绎关系的构建转向了对经典逻辑后承(集)的相干性限制。
三、基于相干性后承的定性确证理论
就其最简形式而言,假说-演绎主义通过表明假说的内容(或其中的一部分)为真来确证该假说,而假说的内容传统上被认为是它的逻辑后承集,即存在这样一种逻辑内容概念:α是β的内容(部分)当且仅当β├α。然而,这一内容概念既不符合我们对内容的直觉,也不符合科学哲学家刻画确证概念的形式需要。基于此概念,我们将得到——任意的两个命题都拥有一些共同的内容——这一荒谬的结论,因为对于任意的两个命题来说,它们的析取式复合命题同时是二者的经典逻辑后承。特别地,对于假说-演绎主义者,说“f=ma∨存在一只白天鹅”是牛顿第二定律“f=ma”的内容从而确证“f=ma”显然是非常不直观的。这样看来,逻辑内容理论的初始动机是构建这样一个后承概念:它不允许析取式的任意析取肢成为它的内容的一部分(11)Ken Gemes,“A New Theory of Content II: Model Theory and Some Alternatives”,Journal of Philosophical Logic,Vol.26,No.4,1997.。假说-演绎主义者在保留经典逻辑有效性的基础上对H-D确证模式中假说的后承集进行限制,认为只有作为相干后承的数据才能成为假说的内容进而确证该假说。
(一)格瑞姆斯(Thomas R.Grimes)的“狭窄后承”(narrow consequence)
基于优布尔析取范式,格瑞姆斯提出了狭窄后承概念:α是β的狭窄后承,当且仅当,β和α各自是一致的并且α的优布尔析取范式的某个析取肢αi满足β├αi(12)Thomas R.Grimes,“Truth,Content,and the Hypothetico-Deductive Method”,Philosophy of Science,Vol.57,No.3,1990.。具体地,p∨q的优布尔析取范式为(p∧q)∨(p∧q)∨(p∧q),但不存在一个析取肢是p(或q)的逻辑后承,所以p∨q不是p(或q)的狭窄后承。可见,狭窄后承概念能够解决析取缝合问题。然而,该概念具有三个主要缺陷:(i)不能解决合取缝合问题;(ii)α∨β不是其自身的狭窄后承;(iii)当α∧β和(α∨β)各自是一致的,那么α∨β是α∧β的狭窄后承。如此一来,我们既得到了想要的结果“Fa∨Gb不确证∀xFx”,也得到了不想要的结果“Fa∨Fb确证∀xFx”。
(二)舒尔茨(Gerhard Schurz)的“相干演绎”(relevant deduction)
舒尔茨认为,在形如“α├α∨β”的推理中β之所以是非相干的,是因为它可以被其他语句替换而仍然保持推理的有效性。为此,基于“不可替换性思想”,舒尔茨提出了“结论相干演绎”概念:α├β是结论相干演绎的,当且仅当,不存在β中的某个谓词,用任何其他的同元谓词替换该谓词在β中的某次出现之后得到β′使得α├β′(13)Gerhard Schurz,“Relevant Deduction”,Erkenntnis,Vol.35,No.1-3,1991.。基于经典逻辑的性质,合取缝合问题和析取缝合问题是对偶的(至少是相似的)。所以,一个自然的想法是:这是否意味着可以通过将结论相干演绎应用于前提来获得一个令人满意的前提相干性定义呢?舒尔茨的回答是否定的。例如,在推理“p∨(q∧q),p→r├r”中,仅仅要求前提中谓词的某次出现不能被其他同元谓词替换是不够的,因为当用t替换前提中q的任意一次出现时推理都将变成无效的。为此,舒尔茨认为,“我们得到了一个前提相干性的定义,它结合了两种不相干的前提:一种是基于单个出现的替换而保持有效性;另一种是基于多个出现的替换而不改变逻辑内容”(14)Gerhard Schurz,“Relevant Deduction”.。基于此,舒尔茨进一步提出了“前提相干演绎”概念:α├β是前提相干演绎的,当且仅当:(i)不存在α中某个谓词,用任何其他同元谓词替换该谓词在α中的某次出现之后得到的α′使得α′├β;(ii)不存在α中的谓词出现,它们被其他同元谓词替换后得到的α′使得α与α′是逻辑等价的。进一步,在提出具体的H-D确证标准时,舒尔茨认为至关重要的一点是:在判定数据陈述和假说陈述之间是否具有H-D确证关系之前,它们应该先各自被其“相干后承元素”(relevant consequence elements)所表示。舒尔茨认为,β是α的相干后承元素,当且仅当:(i)α├β是一个结论相干演绎;(ii)不存在α的结论相干后承的有限集 Δ使得β与Δ的元素的合取逻辑等价并且每一个Δ的元素都比β短(15)Gerhard Schurz,“Relevant Deduction and Hypothetico-Deductivism:A Reply to Gemes”,Erkenntnis,Vol.41,No.2,1994.。例如,∀x(Gx→Fx)不是∀xGx∧∀x(Gx→Fx)的相干后承元素,因为∀xGx∧∀x(Gx→Fx)的相干后承元素是∀xGx和∀xFx。也就是说,∀xGx∧∀x(Gx→Fx)应该被表示为∀xGx∧∀xFx(16)也有科学哲学家使用“部分内容”(partial content)概念表达相同的内涵。,但∀xGx∧∀xFx├Fa也不是前提相干演绎的。
(三)吉姆斯(Ken Gemes)的“内容部分”(content part)
吉姆斯相信,“在一个给定的词汇表中,‘最强后承’(strongest consequence)概念比将后承集作为内容的传统概念更适合成为内容概念的基础”(17)Ken Gemes,“Horwich,Hempel,and Hypothetico-Deductivism”,Philosophy of Science,Vol.57,No.4,1990.。据此,吉姆斯认为,α是β的内容部分,当且仅当:(i)β├α;(ii)α和β是偶真的;(iii)不存在β的一个后承σ使得σ比α强,且任意出现在σ中的原子公式都出现在α中(18)Ken Gemes,“A New Theory of Content I: Basic Content”,Journal of Philosophical Logic,Vol.23,No.6,1994.。根据该定义,p∨q不是p的内容部分,因为存在p的后承即p自身强于p∨q且p中的所有原子公式都出现在p∨q中。但是,内容部分关系并不禁止前提中的非相干合取。为此,吉姆斯基于内容部分给出了理论的“自然公理化”(natural axiomatization)概念。吉姆斯认为,T′是T的自然公理化,当且仅当:(i)T′是一个逻辑等价于T的有限集公式集;(ii)每一个T′的元素都是T′的内容部分;(iii)T′的任何元素的内容部分都不被T′的其他元素所衍推(19)Ken Gemes,“Hypothetico-Deductivism,Content,and the Natural Axiomatization of Theories”,Philosophy of Science,Vol.60,No.3,1993.。
与相干后承元素概念相比,内容部分概念在一些方面会得到不同的结果:(i)依据相干后承元素概念,∃xψ(x,ki)(i=1,…,n)确证∀x∀kψ(x,k)。但对于内容部分概念来说,∃xψ(x,ki)不是∀x∀kψ(x,k)的内容部分,因为存在∀xψ(x,ki)是比∃xψ(x,ki)强的∀x∀kψ(x,k)的逻辑后承且其原子公式都出现在∃xψ(x,ki)中;(ii)假设数据E为“某个物理量μ的值为实数r”并被某个物理理论T所衍推,数据E′为“测量出μ的值位于包含r的实数区间[s,t]内”。直观上,T应该被E′确证,但E′不是T的内容部分,因为E是比E′强的T的后承且其是由E′的词汇构成的。基于这两点,舒尔茨认为吉姆斯的内容部分概念太强(20)Gerhard Schurz,“Relevant Deduction and Hypothetico-Deductivism:A Reply to Gemes”.。然而,在最新论述中,舒尔茨使用“内容元素”(content element)代替了相干后承元素概念,并认为内容部分是由内容元素组成的。关于内容元素概念,舒尔茨指出,“为了确定内容部分,我们需要一种自然地进行合取分解或表示的方法,这种方法将任何语言形式的命题转换为与其逻辑等价的且包含最小语义的基本命题的合取,而这些基本的合取肢被称为内容元素”(21)Michael Schippers,Gerhard Schurz,“Genuine Confirmation and Tacking by Conjunction”,British Journal for the Philosophy of Science,Vol.71,No.1,2018.。
值得一提的是,吉姆斯还对BS进行了修正(22)Ken Gemes,“Bootstrapping and Content Parts”,Erkenntnis,Vol.64,No.3,2006.,但相关工作的实质性内容只是表面上否认了BS的拔靴带特性。吉姆斯虽然认为待检测假说应该独立于背景信息,即不应该要求拔靴带特性,但他同时也认为待检测假说应该实质性地参与到对其事例的推演过程,而这也正是拔靴带特性的精神实质。可见,吉姆斯的方案并没有真正否定拔靴带特性。
四、定性确证理论的两个发展态势
至此不难看出,经过近一个世纪的发展,定性确证理论自逻辑经验主义以来主要经历了“从说明二元确证关系到说明三元确证关系”这一定性确证理论的内部转变和“从对证据和假说(以及理论)之间演绎关系的相干性限制到对逻辑后承集的相干性限制”这一从定性确证理论向逻辑内容理论的外部转变。然而,一方面自然公理化等概念丢失了简单性,而探寻新的演绎关系可能避免使用这样的复杂术语;另一方面乌鸦悖论等语义相干性问题仍未得到解决,需要更强的相干性概念来说明确证关系。为此,定性确证理论出现了以下发展趋势。
(一)从分立走向综合
诚然,无论是相干演绎概念还是内容部分概念都极具启发性,从而被广泛应用到分析哲学的诸多领域,而且对于逻辑后承集的相干性限制也有助于对逻辑后承这一核心逻辑概念的把握。但是,就确证理论本身来说,舒尔茨和吉姆斯等人过于将工作的重心放在对逻辑后承集的相干性说明上,从而忽略了对数据、理论和假说三者之间可能的演绎关系的进一步探讨。而这一局面直到斯普伦格(Jan Sprenger)才被打破,他自觉地将亨佩尔理论和H-D进行了综合,改变了长期以来认为事例确证和H-D是两种互斥的定性确证理论的观念。但是,他所基于的条件“E∧Tcpdev(H,E)”(23)Jan Sprenger,“A Synthesis of Hempelian and Hypothetico-Deductive Confirmation”,Erkenntnis,Vol.78,No.4,2013.斯普伦格使用的条件是“E∧T cpdev(H,E)∧T”,经过简单的演绎推理可以得到“E∧Tcpdev(H,E)”。并没有真正体现亨佩尔事例确证理论的基本观点即“数据陈述衍推假说陈述的展开”,而只是歪打正着地和FC这一限制性条件保持形式一致。当然,斯普伦格的工作启发了我们可以回归对演绎关系的再探讨,而将事例确证和H-D进行综合显然是一种可能的尝试。如果以是否同时承认事例确证和H-D的合理性为区分标准,那么可以将斯普伦格看作是一位定性确证理论的二元论者,而无论是亨佩尔和格莱莫尔等事例确证理论者还是霍维奇、格瑞姆斯、舒尔茨和吉姆斯等假说-演绎主义者都将被看作是定性确证理论的一元论者。当然,梅里尔的预测标准里既使用了满足性标准也使用了预测标准。但一方面,在梅里尔的预测标准中二者之间的关系是不相容析取的;另一方面,梅里尔认为“为了解决‘Pa在几乎任何条件下都可以(尽管不是直接地)确证∀x(Px→Qx)’这一语义相干性问题……,我们可以选择从PCm中省略衍推条件从而获得相同的结果。我认为走这条路是有道理的,但是这样我们就会面临确证存在句的困难”(24)Gary Merrill,“Confirmation and Prediction”.。可见,相较于事例确证,梅里尔还是更倾向于H-D。所以,梅里尔也是一位定性确证理论的一元论者。
(二)由逻辑内容理论走向关于性(aboutness)理论
五、相干性难题的解决出路
除了“由一元论走向二元论”这一综合两种传统和“由逻辑内容理论走向关于性理论”这一深入刻画相干性关系的发展趋势之外,对定性确证标准及对其面临的相干性问题的解答进行反思还发现:首先,从纵向的角度来说,在提出确证标准或对其进行评判时,科学哲学家通常只是诉诸是否满足直觉上的相干性,并未对相干性概念本身作详细深入的界定;其次,从横向的角度来说,科学哲学家没有深入讨论定性确证标准特别是事例确证标准和作为定量确证标准的概率提高原则之间的关系;再次,就确证标准具体的限制条件而言,格莱莫尔所要求的极具合理性的拔靴带特性却被目前最受欢迎的H-D确证模式和贝叶斯主义所拒斥;最后,就确证理论所基于的形式工具而言,作为哲学逻辑新分支的图式逻辑并不像符号逻辑这样成为一种重要的解题工具。基于此,本文提出了“对相干性概念自身的界定”、“定性确证标准的定量表征”、“拔靴带特性的合理性”和“图式逻辑的波普尔(Karl Popper)式结论”等问题供进一步探讨,它们可能是真正解决相干性问题从而构建良好确证理论的极具前途的方案。
(一)相干性概念自身的界定
虽然相干性关系不足以说明确证关系,但却是说明确证关系的基础。考察合取缝合问题和析取缝合问题不难发现,这两个问题目前不仅分别只是针对假说和证据的,而且也只是针对H-D的。如果将事例确证和H-D进行综合,那么势必需要对两种确证模式的基本形式特征进行考量。又由于缝合问题的产生根源于经典逻辑的性质,即对前提进行合取或对结论进行析取都可以保持原有推理的有效性。所以,这又势必会引起对缝合问题的进一步说明。本文认为,缝合问题应当细分为四种:假说析取缝合问题、证据析取缝合问题、假说合取缝合问题和证据合取缝合问题。基于两种定性确证标准的形式特征和经典逻辑的性质,可以得到PC和SC各自所面临的缝合问题,如表1所示:

(表1) PC和SC所面临的四种缝合问题
其中,“—”表示该问题已被相应的模型所避免;“√”表示该问题仍有待解决。可见,前三个缝合问题分别可以被PC或SC所避免。也就是说,如果将事例确证和H-D综合从而得到一个新的确证标准,那么所需要解决的就只有“证据合取缝合问题”:如果E确证H,那么对于任意与E一致的K,E∧K也确证H,但是K可以是与H非相干的。如果该问题成立,那么将可以避免“绿蓝悖论”。因为绿蓝悖论的症结在于“Ea∧Ot≤Ta∧Ba”(一只在时刻T之前被观察的黑乌鸦)这样的数据会同时确证绿假说“∀x(Ex→Gx)”(所有翡翠都是绿的)和绿蓝假说“∀x(Ex→Gruex)”(所有翡翠都是绿蓝的)这样两个具有竞争性的假说。其中,Gruex=(Ot≤Ta→Gx)∧(Ot≤Ta→Gruex)。而显然此时如果接受Ea∧Ot≤Ta∧Ba确证∀x(Ex→Gx),那么将导致证据合取缝合问题,因为Ot≤Ta相对于∀x(Ex→Gx)来说是非相干的。当然,这种对绿蓝悖论的消解方案虽然符合国内学者顿新国对确证研究的证据转向这一指认(27)参见顿新国:《绿蓝悖论的证据路径消解方案》,《科学技术哲学研究》2020年第3期。,但也是基于对证据合取缝合问题之成立的辩护。也就是说,问题的关键在于假说合取缝合问题和证据合取缝合问题等相干性问题是否是真问题,而对此的说明又基于对相干性概念本身的界定。
(二)定性确证标准的定量表征
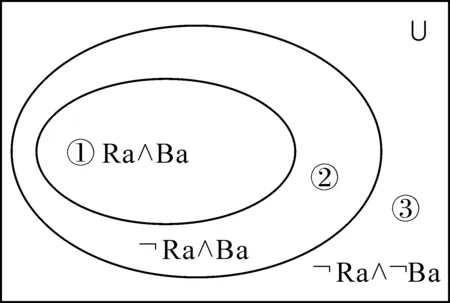
定量确证标准是通过概率值的大小比较来说明相干性的。基于“概率提高原则”这一定量确证标准,菲特森(Branden Fitelson)曾提出了一个针对“证据具有传递性”这一论题的所谓反例(28)Branden Fitelson,“Evidence of Evidence is Not (necessarily) Evidence”,Analysis,Vol.72,No.1,2012.:从一副无大小王的扑克牌中随机抽出一张牌a,关于这张牌可以有三个命题:E1“a是一张黑色的牌”;E2“a是一张黑桃A”;E3“a是一张A牌”。具体地,由于Pr(E2/E1)=1/26,Pr(E2)=1/52,Pr(E2/E1)>Pr(E2),E1提高E2的概率,所以E1是E2的证据;有由于Pr(E3/E2)=1,Pr(E3)=1/13,Pr(E3/E2)>Pr(E3),E2提高了E3的概率,所以E2是E3的证据;但Pr(E3/E1)=1/13,Pr(E3)=1/13,Pr(E3/E1)=Pr(E3),E1未提高E3的概率,所以E1不是E3的证据,这就驳倒了“证据具有传递性”的论断。然而,该反例是不成立的,因为这种表面的概率提高掩盖了E1和E2之间、E2和E3之间不同的演绎关系:E2E1且E2E3。也就是说,E1提高E2的概率所依据的是H-D确证标准,而E2提高E3的概率所依据的则是事例确证标准。不难发现,造成这种差异的原因在于Pr(E3/E2)=1。也就是说,在E2和E3的关系中,我们实际上无需知道E3的验前概率Pr(E3),而仅由E2 (图1) ∀x(Rx→Bx) (图2)∀x(Rx↔Bx) (图3)∀x(Bx→Rx) 作为一种图式逻辑,欧拉图可以直观地表示假说所做断言下全域U的结构。根据假说H1和H3,全域U被划分为三个不相交的区域{①,②,③};而根据假说H2,①和②是重合的。在每个图中,不仅E均落在③中,而且③的大小和位置均保持不变。也就是说,改变假说Hi(i=1,2,3)只会影响①和②的相互关系却不影响③的大小和位置,亦即假说Hi所做断言并不涉及Rx∧Bx所决定的对象类,这表明假说Hi和Ra∧Ba是不相干的,而不相干的两个对象之间将更不会有确证关系。因此,形如“Ra∧Ba”的观察报告将不会确证形如“∀x(Rx→Bx)”的假说。进一步,在图1中,Ra∧Ba不落在任何一个区域中,即假说H1所作断言表明Ra∧Ba是不存在的。所以,如果观察报告为Ra∧Ba,其将否证H1。可见,我们在拒绝Ra∧Ba确证∀x(Rx→Bx)而肯定Ra∧Ba否证∀x(Rx→Bx)时,重新走向了一种波普尔式的观点:上图中所体现的不对称之处在于,“否证性的观测结果使我们能够对被检测的理论得出有效的结论,而确证性的观测结果却不能”(31)Ray Scott Percival,“Confirmation versus Falsificationism”,Robin L.Cautin,Scott O.Lilienfeld,eds.,The Encyclopedia of Clinical Psychology,New York:John Wiley & Sons,Inc.,2015,p.5.。可见,如果拔靴带特性的合理性意味着我们必须在几种确证标准当中做出选择,那么此处所展示的图式逻辑的波普尔式结论则对确证概念本身的内涵提出了挑战。 综上,为了避免相干性难题,事例确证和H-D这两种传统的定性确证理论不仅经历了“从说明二元确证关系到说明三元确证关系”这一定性确证理论的内部转变和“从对证据和假说之间演绎关系的相干性限制到对逻辑后承集的相干性限制”这一(传统)定性确证理论向逻辑内容理论的外部转变,也出现了“由一元论走向二元论”这一综合两种定性确证理论传统和“由逻辑内容理论走向关于性理论”这一深入刻画相干后承集的发展态势。在此基础上,对相干性概念自身的界定、定性确证标准的定量表征、拔靴带特性的合理性和图式逻辑的波普尔式结论等问题和方案的探讨也有助于推动对相干性难题的解决和定性确证理论的发展。 当然,在最小限制的情况下描述出一个简约的且能够刻画具有相干性的确证关系是科学哲学家和分析哲学家们始终如一的追求。而无论哪一种具体的确证模式,它们都是通过假说与其肯定事例之间的某种推理关系来体现确证关系的。所以,定性确证理论实质上是对相干性推理关系的逻辑句法和语义研究,其主要任务是给出前提与结论之间的相干性关系。众所周知,只有当推理关系具有有效性时该推理关系才被称为“衍推关系”,相应地,结论被称为逻辑后承。然而,衍推关系并不能很好地刻画我们的相干性直觉,它将导致本文所述的各种相干性问题。为此,我们需要对衍推关系添加更多的性质,来增强前提和逻辑后承之间的相干性关联。自格瑞姆斯以来、经吉姆斯发展、直到费恩(Kit Fine)和亚布洛等人系统化和精确化的逻辑内容理论的主要任务便在于此。比照科学哲学中的“部分真”(partial truth)这一经典概念,费恩和亚布洛明确地将“部分内容”(partial content)作为逻辑内容理论研究的核心。而无论哪一种部分内容概念,它们都认为只有当逻辑后承是前提的内容的一部分时,逻辑后承才能被称为前提的部分内容。也就是说,逻辑内容理论实质上是基于对“整分关系”(mereological relation)的认知来说明部分内容概念的。如此一来,推理关系就从衍推关系上升为整分关系,而处于整分关系之中的前提与结论之间也就具有了更强的相干性关联。可见,存在一个将推理关系依次上升为衍推关系和整分关系的“相干性层级”(relevance hierarchy),构成了由定性确证理论向逻辑内容理论转变的基本线索。当然,是否存在比整分关系更具相干性的推理关系,以及整分关系应该具有哪些基本性质,都将成为逻辑内容理论进一步发展甚至转变的动力和方向。(三)拔靴带特性的合理性

(四)图式逻辑的波普尔式结论


六、结语

