利用对称巧求重积分

尤 晓 琳

(郑州工程技术学院基础科学学院， 郑州 450044 )

高等数学中多重积分的计算无疑是重点内容之一。教学中，有些重积分计算如果不利用对称性计算相当繁琐，甚至做不出来。许多学生在考研备考时，常常提到这个问题，但现使用的教材[1]中未具体给出。为了提高重积分的运算速度，也为了进一步加深对重积分概念、计算的理解。本文总结了[2][3]利用对称性求重积分的方法。

注：以下积分域都为有界闭区域，所给被积函数在积分域上有界、连续。

一、利用积分域的对称性及被积函数奇、偶性计算重积分

1.二重积分中的结论

(1)二重积分中积分域D关于y轴对称，被积函数对x具有奇、偶性，则，

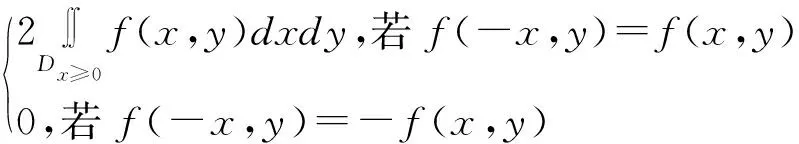
证明：因为积分域D关于y轴对称，不妨设D={(x,y)|-a≤x≤a,φ1(x)≤y≤φ2(x)}

因为积分域D关于y轴对称，φ1(-t)=φ1(t),φ2(-t)=φ2(t)，

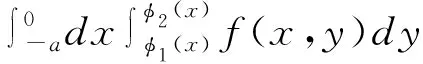
(2)二重积分中积分域D关于x轴对称，被积函数对y具有奇、偶性，则

证明同上

解：本题中区域D虽然既不关于x轴对称，也不关于y轴对称，被积函数也不具有奇、偶性，但是函数f(x,y)=xy5既是x的奇函数，又是y的奇函数，区域D上加条辅助线(如图)后，D1关于x轴对称，D2关于y轴对称，则

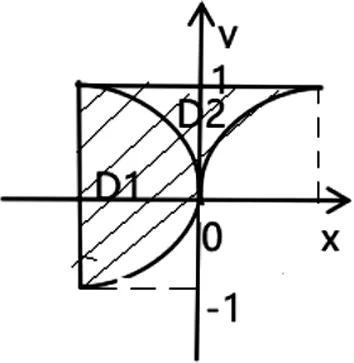
解：由题意累次积分化成二重积分的积分域D由曲线：y=2-x2,y=-x,y=x围成(如图)，则

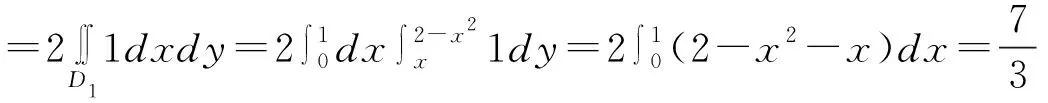
2.三重积分中的结论

(1)三重积分中积分域关于xoy面对称，被积函数对于z坐标有奇、偶性，则，

(2)积分域关于xoz面对称，被积函数对于y坐标有奇、偶性，则，

(3)积分域关于yoz面对称，被积函数对于x坐标有奇、偶性，则，

证明类二重积分略

例3：已知D={(x,y,z)|x2+y2+z2≤1,

x≥0,y≥0},

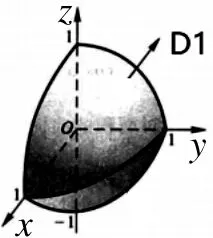
解：积分域D关于xoy面对称，f(x,y,z)=3xyz关于z坐标是奇函数，

f(x,y,z)=x2+y2+z2关于z坐标是偶函数

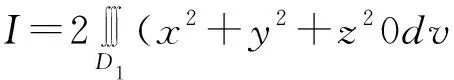
二、利用积分域中变量的对称性求重积分

1.二重积分中积分域D关于两个变量对称(即积分域关于y=x对称)

酒精性肝病的治疗方面，马萨诸塞大学医学院Szabo（摘要LB-1）一项多中心随机双盲安慰剂对照的临床试验报道了IL-1受体激动剂联合己酮可可碱和锌治疗重症酒精性肝炎28 d，终点指标为30 d、90 d及180 d的病死率，与甲泼尼龙（32 mg每日口服，28 d）比较，短期疗效相近，长期疗效新的治疗更有优势。

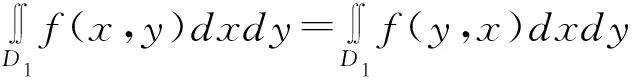
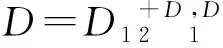
设D1={(x,y)|a≤x≤b,x≤y≤φ(x)},D2={(x,y)|a≤y≤b,x≤y≤φ(y)≤x≤y}

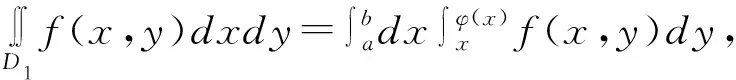
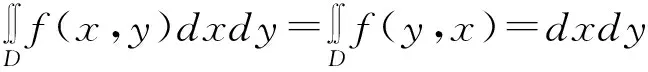
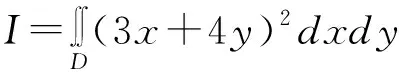
∵D={(x,y)|x2+y2≤1}关于y=x对称

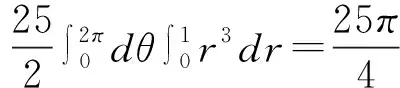
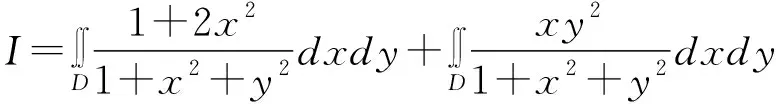
∵D={(x,y)|x2+y2≤1,x+y≥0}关于y=x对称

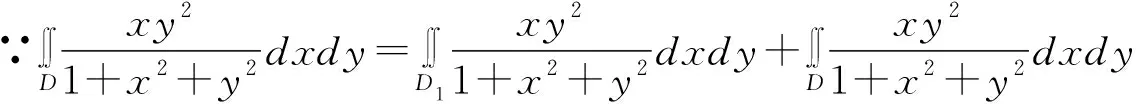
2.三重积分中积分域D关于变量对称(任意交换两个变量位置积分域不变)

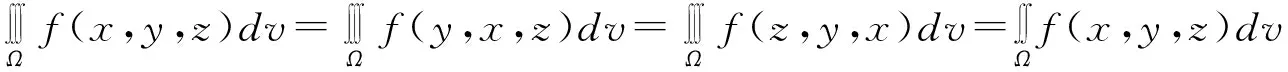
(证明类似二重积分略)

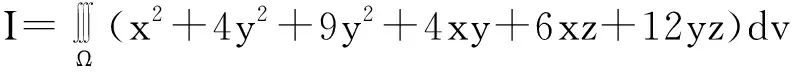
又∵Ω={(x,y,z)x2+y2+z2≤1}关于x,y,z对称

重积分的运算对于本科生来说是个重点又是难点，对于大多数学生，被积函数复杂些，算不出来积分，如果充分的掌握了对称性，不但可以简化做题的步骤、减少做题的时间，还能提高学生学习重积分的兴趣。