例谈未定式求极限的精讲多解模式的研究

邢 喜 莲

(广州工商学院通识教育学院， 广州 510850)

一、问题提出

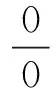
二、精讲多解的课例研究

宋代著名数学家、教育家杨辉：“好学君子自能触类而考，何必轻传”，他认为，学生的学习应该触类旁通，不需要所有的东西都由教师轻易传授, 人本主义提倡内在学习，认为应依靠学生内在驱动去自觉、主动、创造性学习。构建主义认为，学习不是知识从外到内的传递，而是人积极主动构建的过程。追求精力投入和知识、能力增长的最大化, 教师“精讲”，为学而讲，为掌握洛必达法则及公式而讲，引发学生思考从而寻找解决问题的方法，进而提升思维能力。

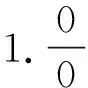
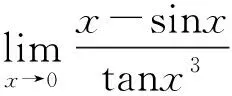
分析2 结合重要公式求解。

分析3 结合等价无穷小求解。

精讲多解，精讲重难点，在“讲得精”“讲得新”“学得好”上下功夫[5]。需要教师引导学生从问题的条件出发，寻找解决问题的思路，形成一个层层递进的问题链，通过特例、试错等方法可否找到解决问题的思维方法并反思是如何想到这个方法的，依赖于学生解题的熟练程度。

2.0·∞型的未定式

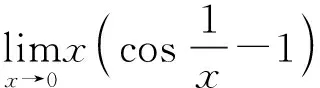
精讲多解，需要教师的引导、帮助和支持，体现学生在学习过程中的主体地位和教师在教学过程中的主导作用，两者缺一不可，主导主体相结合，否则，难以取得解题实效。

3.(∞-∞)型的未定式

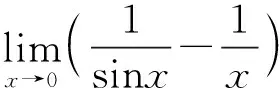
分析2 用等价替换公式，重要极限，洛必达法则，三角公式。

4.1∞型的未定式

分析1 这是因为数列不是连续变化的，从而更无导数可言，即对数列求导数是无意义。

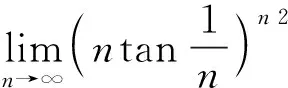
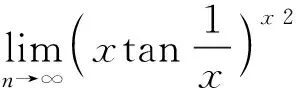
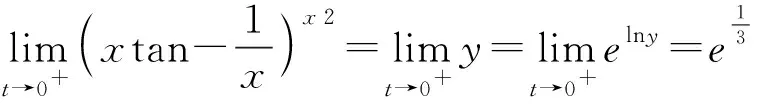
分析2 利用重要极限

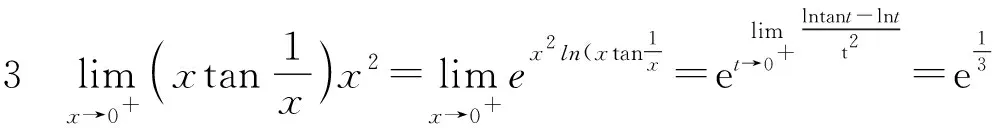
对于未定式1∞型，∞0型，00型这三种类型，实际是幂指函数[u(x)]v(x)的未定式问题，可利用关系式uv=evlnu求之，对于较复杂的式子，可以先求式子取对数后的极限。

一题多解是一个不断摸索、探讨、猜想、推理、检验的过程。多解不仅是为了固化概念、法则、公式，更能达到培养学生运用正确方法解决数学问题的能力。

三、结语

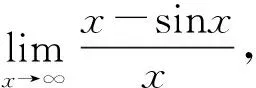
多解要在构思上下功夫，在审题上做文章. 有的题目往往以复杂的外壳来掩盖知识的内在联系，特别是有些综合题，涉及到的知识常常改变原来的面目，难以抓住思路、主线、无法确定解题策略，或策略不当，实施繁难，或实施解题策略中遇到障碍，不能自我排除，导致出现错误，但错误是重要的数学教学资源，它揭示了数学理解上的误区与盲点，有些题目解题的方法是多样的，矫正的策略也是多样的，有时需要将多种矫正策略配合起来，灵活运用[7]。但是，抓住题目条件和结论中所涉及的知识点去构思是不能动摇的，在构思中有的需要整体分析能力及结构特征[8]。有的需要利用特殊、有用的经验联想等。课堂是良性交流互动的空间，教师只管讲、学生只管听的课堂已不能满足教学要求。教师不但要管讲，而且要精讲、多解、有效互动解题[9]。使学生对所学的内容进一步 “学活”“学懂”“学深”[10]。