中考“隐形圆”专题复习探究

江苏镇江市丹徒区支显宗学校（212000）徐海波 高英

在历年的中考试题中，经常出现一类几何题，将圆隐藏在已知几何条件里，学生需要根据相关的条件分析与探索，恰当地构造出这个圆，然后利用圆的相关性质与特点进行求解。本文结合典型的几种含“隐形圆”条件的中考题，总结出此类题型的解题策略与方法，以期使中考复习获得事半功倍的效果。

一、利用圆的概念，化繁为简

圆的定义：在同一平面内，到定点的距离等于定长的点的集合叫作圆。定点为圆心，定长为半径。根据圆的定义，可以发现题目中符合圆的特征的部分：定点加定长产生“隐形圆”。我们可以构造辅助圆解决问题。具体地，如图1，若OB=OC=OD=OE=OF，则B，C，D，E，F在同一个圆上。

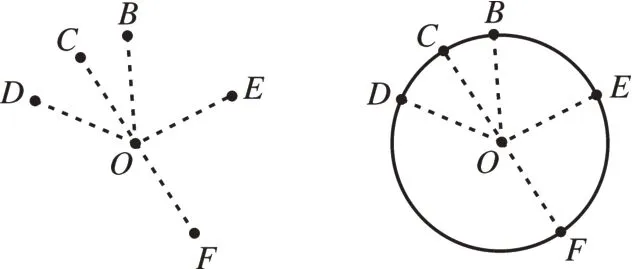
图1

［例1］（2019 年山东德州中考题）如图2，点O为线段BC的中点，点A，C，D到点O的距离相等，若∠ABC=40°，则∠ADC的度数是（ ）。

A.130° B.140° C.150° D.160°

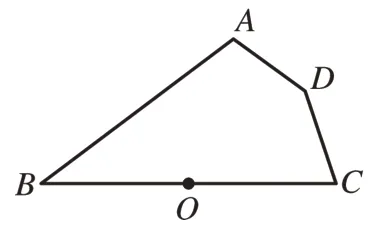
图2

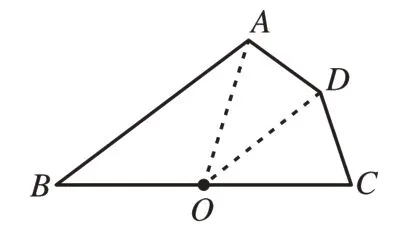
图3

解法1：常规解法。如图3，连接OA、OD。利用等腰三角形“等边对等角”与“四边形AOCD的内角和是360°”的性质，由∠ABC=40°，得2∠ADC=360°-80°=280°，最后求出∠ADC=140°。故选B。

因为本文重点研究的圆的相关性质的利用，上述方法有些繁杂，所以这里不做详细论述。

解法2：利用辅助圆的方法。根据题意，点O到点A、C、D的距离相等，O为BC的中点，根据圆的定义可知，A、B、C、D四点是在以O为圆心，OC为半径的圆上，作出辅助圆（如图4），辅助圆是四边形ABCD的外接圆，根据“圆内接四边形对角互补”的性质，∠ABC与∠ADC互补，由∠ABC=40°，轻松得出∠ADC=140°，因而选B。

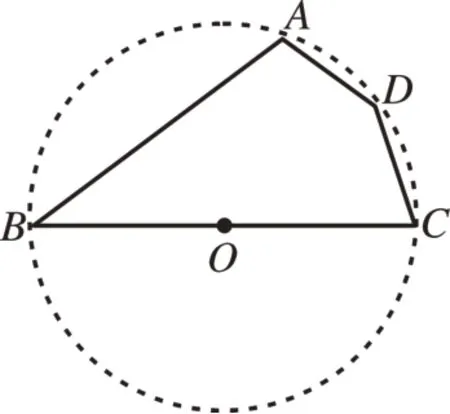
图4

二、巧用“对角互补的四边形”揭示“隐形圆”的本质

如果一个四边形的对角互补，那么这个四边形一定内接于圆。具体地，如图5，若∠A+∠C=180°或∠B+∠D=180°，那么四边形ABCD内接于圆O。

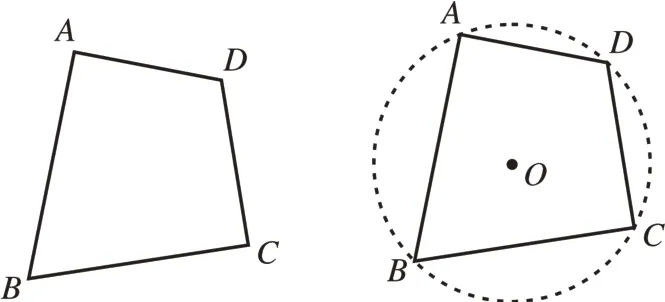
图5

［例2］（2017 年福建中考题）如图6，矩形ABCD中，AB=6，AD=8，P、E分别是线段AC、BC上的点，且四边形PEFD为矩形。

（1）若△PCD是等腰三角形，求AP的长；

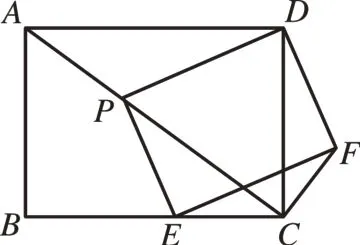
图6

（2）若AP=，求线段CF的长。

分析：第（1）小题只要求出PC，根据等腰三角形的三种情况，利用等腰三角形的轴对称性讨论计算即可得出结论，这和本文研究的内容联系不大，故略去不写。下面重点介绍如何利用“隐形圆”求解第（2）小题。

解：（1）略；

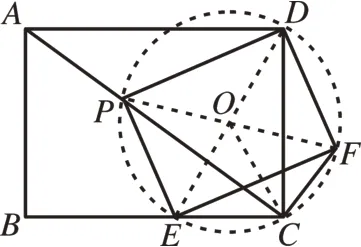
图7

（2）如图7，连接PF，DE，记PF与DE的交点为O，连接OC，由四边形ABCD和PEFD是矩形，利用矩形的性质，可以求出OC=。在矩形PEFD中，对角线相等，即PF=DE，由此可以求出OC=OP=OF，根据三角形内角和可知△PCF的内角和是180°，2∠OCP+2∠OCF=180°，∠PCF=90°，可知∠PCD+∠FCD=90°，△PCF是直角三角形。在Rt△ADC中，∠PCD+∠PAD=90°，可以得出∠PAD=∠FCD，在△ADP和△CDF中，三个角都相等，所以△ADP∽△CDF，可以得出，又已知AP=，可以轻松得到CF=。

三、利用“动点到定点的距离为定长”解题

如果一个动点到一个定点的距离为定长，那么这个动点的轨迹为一个圆。具体地，如图8，OA⊥OB，垂足为O。P，Q分别是射线OA，OB上的两个动点，且PQ为定长。点M是线段PQ的中点，那么动点M的轨迹是圆的一部分。

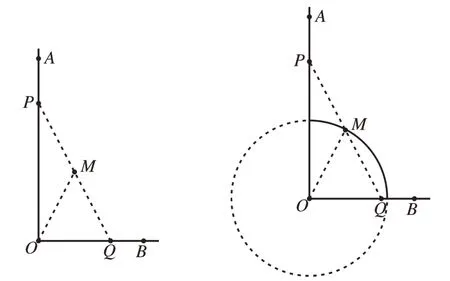
图8

［例3］如图9，在矩形ABCD中，已知AB=2，BC=3，现有一根长为2 的木棒EF紧贴着矩形的边（即两个端点始终落在矩形的边上），按逆时针方向滑动一周，则木棒EF的中点P在运动过程中所围成的图形的面积是多少？

分析：木棒EF的中点P在运动中的轨迹为分别以A、B、C、D为圆心，1 为半径的四条弧和FG和HI组成的封闭图形。它的面积可以用矩形面积减去四个扇形的面积求得。此题难点主要是P点的轨迹是“隐形圆”。

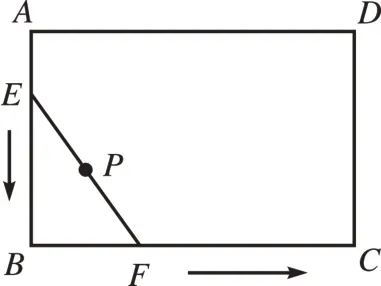
图9

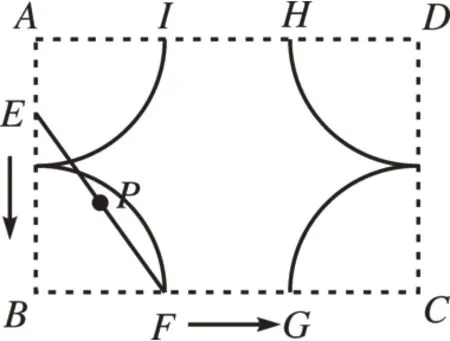
图10

解：如图10 所示，当木棒EF与EB，BF组成三角形，根据“直角三角形斜边上的中线等于斜边的一半”得出点P到点B的距离始终为1，所以点P的运动轨迹是圆或者圆的一部分。通过作图发现是个圆。同理可证木棒EF在其他三个角落时情况是一样的。在矩形的“长”上运动的轨迹分别为FG和HI，所以木棒EF的中点P在运动中的轨迹为分别以A、B、C、D为圆心，1 为半径的四条弧和FG和HI组成的封闭图形，故所围图形的面积等于矩形面积减去4 个扇形面积，即S=6 -4 ×=6 -π。

四、运用“定长对定角”的“隐形圆”模型解题

如图11所示，若有一固定线段AB及线段AB所对的∠C大小固定，根据圆的知识可知，点C并不是唯一固定的点，点C在⊙O的弧ACB（至于是优弧还是劣弧取决于∠C的大小）。∠C＜90°，则点C在优弧上运动；∠C=90°，则点C在半圆上运动；当∠C＞90°，点C在劣弧上运动。

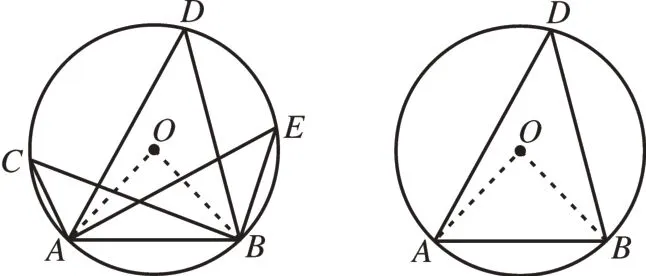
图11

［例4］如图12，△ABC是等边三角形，AB=2，若P为△ABC内一动点，且满足∠PAB=∠ACP，则线段PB长度的最小值为_______。

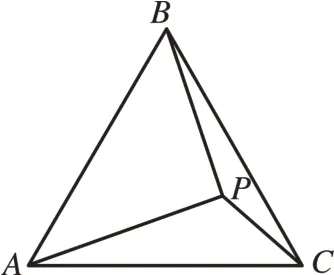
图12

分析：由等边三角形的性质得出∠ABC=∠BAC=60°，AC=AB=2，求出∠APC=120°，由此可得AC=2为定长，∠APC=120°为定角，如图13，因而点P的轨迹为“圆心为O，半径为AO的‘隐形圆’”的一段劣弧。由圆外一定点到圆上点的最小值的知识可知，连接圆心O与定点B的线段与圆的交点就是所求的最小值时的点P，如图14。当PB⊥AC时，PB长度最小，设垂足为D，此时PA=PC，由等边三角形的性质得出AD=CD=AC=1，∠PAC=∠ACP=30°，∠ABD=∠ABC=30°，求 出PD=AD·tan30°=，BD=AD=，即可得出答案。

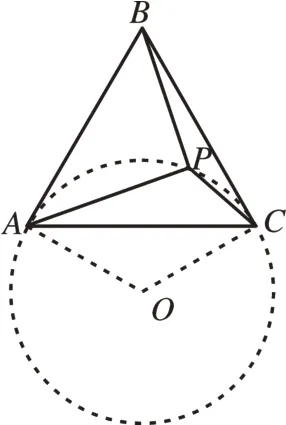
图13

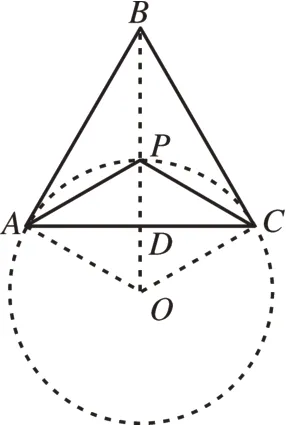
图14

解：∵△ABC是等边三角形，

∴∠ABC=∠BAC=60°，AC=AB=2，

∵∠PAB=∠ACP，

∴∠PAC+∠ACP=60°，

∴∠APC=120°，

∴点P的运动轨迹是

五、转化变量，利用“隐形圆”解决最值问题

如图15 所示，对于一个定点P和一个动点之间的最值问题，若动点的运动轨迹为⊙O，⊙O的圆心O与定点P之间的距离加上或减去半径，就可以求出线段的最大值PB和最小值PA。因此，解这类题，最常作的是辅助圆，找出辅助圆所在的圆心，连接圆心与定点之间的线段，再求出圆心与定点之间的距离，用其减去或加上半径即可求出最值。

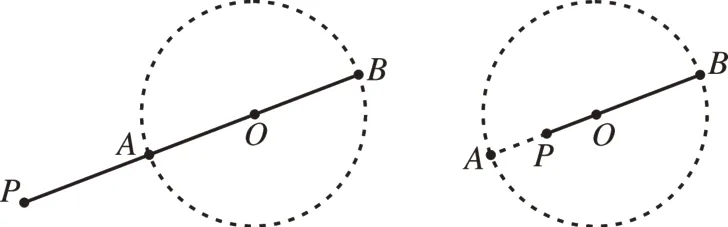
图15

［例5］如图16，矩形ABCD中，AB=2，AD=3，点E、F分别AD、DC边上的点，且EF=2，点G为EF的中点，点P为BC上一动点，则PA+PG的最小值为________。

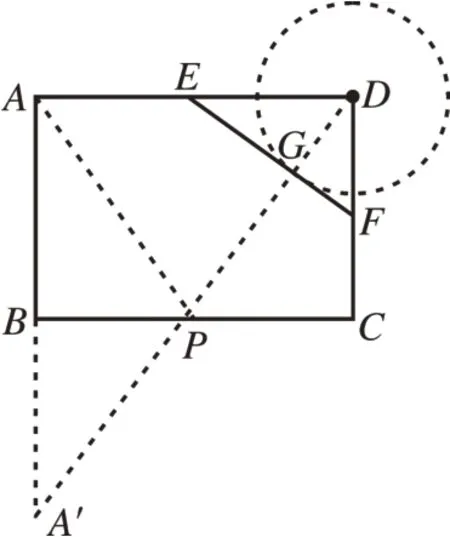
图16

分析：本题主要考查运用轴对称将折线变成直线解决线段最值的问题，分析判断出点G的运动轨迹是解答本题的关键。直角三角形EFD的斜边EF，点G为EF的中点，并且EF=2，根据“直角三角形斜边上的中线等于斜边的一半”可以得出DG=1。其中D为定点，DG=1 为定长。由此可得出点G在以D为圆心，以DG为半径的圆上，这就是本题的“隐形圆”，EF与圆的交点就是点G。利用轴对称，作点A关于对称轴BC的对称点A′，连接A′D，可知A′D必与BC交于点P，与EF必交于点G（通过全等三角形可以验证），此时PA+PG的值最小，这个最小值就是A′G的长；△ADA′为直角三角形，由勾股定理可以求得A′D的长度，用A′D的长度减去⊙D的半径，即可得出本题的答案。

解：∵EF=2，点G为EF的中点，∴G是以D为圆心，以DG=1 为半径的圆上的点，此点也是EF的中点。

作点A关于对称轴BC的对称点A′，连接A′D，交BC于P，交EF于点G，

根据“两点之间线段最短”，可知PA+PG的值最小，由图可知，此时PA+PG=A′D-DG，

∵AB=2，∴AA′=4，又∵AD=3，

在直角△ADA′中，由勾股定理可得A′D=5，

∴A′G=A′D-DG=5 -1=4，

∴PA+PG的最小值为4。

圆具有直观、形象的特点。解决“隐形圆”的问题时，要根据点、线、角的特定关系发现“隐形圆”的图形本质。在此过程中，挖掘隐含条件，把“隐形圆”显现出来，再有效利用其他几何图形的概念、定义与性质是破解题目的关键。