一类数列问题的解法探讨

江苏徐州市第三中学（221005）刘书霞

数列作为一类特殊的函数表现形式，具有独特的性质，是知识交汇、问题创新的纽带，也是高考的重点和难点之一。高考数列题以数列为问题背景，融合其他相关知识来设计综合问题，充分体现了高考命题的指导思想，有效考查了相应的数学知识，考查了学生的抽象概括能力、逻辑推理能力，以及数学抽象、数学运算、逻辑推理等核心素养。

一、问题呈现

［例1］已知数列{xn}满足x1=2，xn+1=(n∈N*)。给出以下两个命题。

命题p：对任意n∈N*，都有1 ＜xn+1＜xn；

命题q：存在r∈（0，1），使得对任意n∈N*，都有xn≤rn-1+1，则（ ）。

A.p真，q真 B.p真，q假

C.p假，q真 D.p假，q假

此题是涉及根式型递推数列关系的一道综合题，它巧妙地把函数、数列与常用逻辑问题合理融合。学生要结合数列的相关知识来分析与推理，才能判定对应命题的真假。此类问题对学生的应用能力、分析问题与解决问题的能力及逻辑推理能力要求比较高。

二、问题破解

（一）对于命题p的判断

方法1：（作差比较法+极限特征）

而当xn→1时，xn+1→1且xn+1＞1，

对任意n∈N*，都有1 ＜xn+1＜xn，即命题p为真命题。

点评：作差法是中学数学中比较大小的常用方法，具有实用性和通法性。运用作差法，能够培养学生的发现与观察能力及类比意识。

方法2：（放缩法+同号性）

那么xn+1-1与xn-1的符号相同，

而x1-1=1 ＞0，则有xn-1 ＞0，即xn＞1。

对任意n∈N*，都有1 ＜xn+1＜xn，即命题p为真命题。

点评：用放缩法证明数列不等式是数列中的难点内容。放缩法灵活多变，技巧性要求特别高。放缩是一种能力，放缩要有度，如何恰到好处，是放缩法的精髓和关键所在。

方法3：（同号性+作差比较法）

由xn+1=，可 得=2xn-1，即-1=2(xn-1)，

整理可得(xn+1-1)(xn+1+1)=2(xn-1)，

那么xn+1-1与xn-1的符号相同。

而x1-1=1 ＞0，则有xn-1 ＞0，即xn＞1；

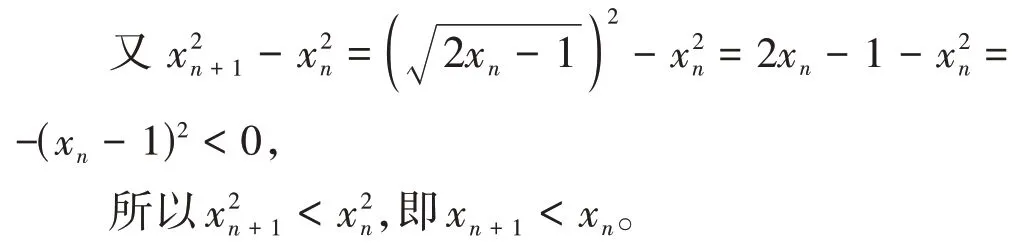
对任意n∈N*，都有1 ＜xn+1＜xn，即命题p为真命题。

方法4：（数学归纳法+作差比较法）

（1）当n=1时，x1=2 ＞1；

（2）假设当n=k(k∈N*)时，不等式xk＞1成立，那么=1 成立，即 当n=k+1时，不等式xk+1＞1也成立。

根据（1）和（2），可知对任意n∈N*，都有xn＞1成立；

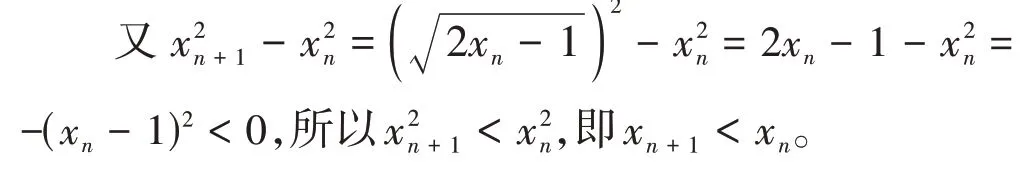
对任意n∈N*，都有1 ＜xn+1＜xn，即命题p为真命题。

点评：数学归纳法是一种重要的数学证明方法，通常被用于证明某个给定命题在整个（或局部）自然数范围内成立。运用数学归纳法可有效解决数列问题。

方法5：（“蛛网图”法）

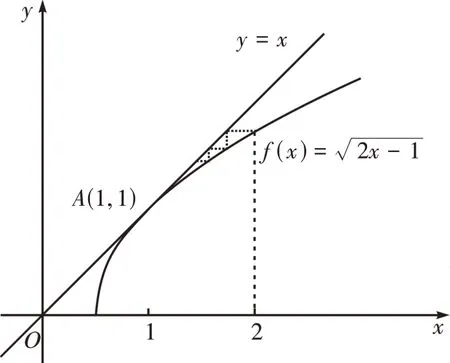
图1

点评：对于一个不可求通项公式的数列递推关系的范围确定问题，利用作差比较法、放缩法、数学归纳法等常见的方法，并借助“同号性”等不等式的性质来处理，可以有效破解问题。而“蛛网图”是解决此类问题比较特殊的方法，其常借助特征函数的图像与性质，数形结合，准确判定。

（二）对于命题q的判断

方法1：（裂项法+反证法）

方法2：（极限特征法）

由xn≤rn-1+1，可得xn-1 ≤rn-1，那么，构造函数f(x)=，此函数在定义域上单调递减，所以自变量x从2→1 的过程中单调递增，由于任意n∈N*，而x无法取到1，则函数f(x)无最大值，那么r不存在，所以不存在r∈(0,1)，使得对任意n∈N*，都有xn≤rn-1+1，因此命题q为假命题。

方法3：（“蛛网图”法）

由xn≤rn-1+1，可得xn-1 ≤rn-1，那么=r，即需要满足(xn-1,xn)与(1,1)两点之间的斜率始终小于一个在(0,1)之间的确切数值r，如图2 所示，随着n的增大，此斜率一直在递增，且无限接近于1，故必须满足r≥1，所以不存在r∈(0,1)，使得对任意n∈N*，都有xn≤rn-1+1，所以命题q为假命题。

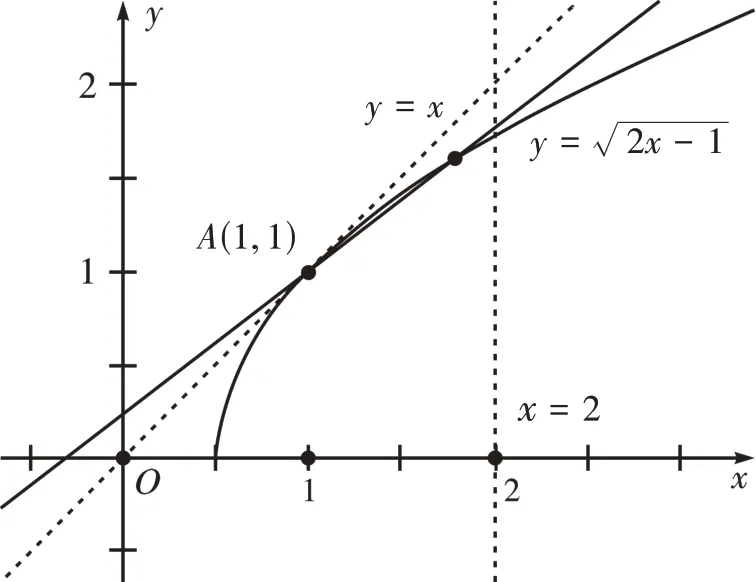
图2

点评：根据存在性问题的判定特征，可以借助反证法加以判断，而涉及数列通项的变形与应用，可以利用裂项、累加等数列求和方式来处理，进而结合极限特征等方法来判断。同样，构建等比数列，从“蛛网图”的视角，结合几何意义来判断，借助斜率，数形结合，也可做出直观的判断。

综上可知，命题p为真命题，命题q为假命题，故选B。

在破解以数列为背景的综合性问题时，往往要充分展示数列的函数特征，通过回归函数的基本性质与基本方法，结合数列的基本特征来分析，从而达到知识与方法的巧妙融合。同时，要抓住函数的模型与相关知识，以及特殊数列模型，运用逻辑推理方法来分析与处理，使得问题指向明确，方便转化。

三、方法应用

解决线性根式型递推数列问题有特征根法和不动点法。而非线性递推数列问题是各种竞赛的难点和考试的热点，这类问题可以借助作差比较法、极限特征法、“蛛网图”法和数学归纳法解决比如下面两题。

1.数列a0,a1,a2,…与b0,b1,b2,…,定义如下：