中考探究型试题的考向研究

广西天峨县中学（547300）付小玲

近几年中考，考查学生动手操作能力的探究型试题在逐年增加。此类试题集动手操作与新知探究于一体，需要学生通过前期的观察与分析，中期的操作、比较与猜想，后期的抽象与概括等，灵活运用课本知识与生活经验解决问题。这类试题有利于培养学生的创新意识、直觉思维与综合实践能力。

一、利用图形变换作图

平面几何图形的变换主要包括平移、旋转、轴对称、位似等。利用平移作图，就是把一个图形沿规定的方向移动一定的距离，平移前后的两个图形全等，对应线段平行或在同一直线上，且图形各部分所处的方位不变；利用旋转作图，就是把一个图形绕一个固定点按顺时针或逆时针转动一定的角度，旋转前后的两个图形全等，对应点连线的中垂线经过旋转中心，每组对应点与旋转中心连线的夹角都等于旋转角；利用轴对称作图，就是把一个图形沿一直线翻折，翻折前后的两个图形全等，对应点的连线被对称轴垂直平分，对应线段或所在直线如果相交，交点在对称轴上；利用位似作图，就是把一个图形按规定的比例放大或缩小，位似前后的两个图形相似，对应线段平行，对应点的连线经过位似中心。

［例1］如图1，已知△ABC的三个顶点的坐标分别为A(3,3)，B(-1,0)，C(4,0)。

（1）如果将△ABC平移，使点O与点A重合，那么平移后点C的对应点C1的坐标是多少？

（2）将△ABC以点B为中心逆时针旋转90°，画出所得的三角形。

（3）以点A为位似中心放大△ABC，得到△AB2C2，使S△ABC∶S△AB2C2=1∶4，在图中画出△AB2C2。

图1

分析：（1）因为平移后点A与点O重合，点A的坐标为（3，3），点O的坐标为（0，0），所以点A需要向下平移3 个单位，再向左平移3 个单位。因为点C的坐标为（4，0），向下平移3 个单位，向左平移3个单位，得点C1的坐标为（1，-3）。

（2）直接利用旋转的性质得出对应点位置，进而画出图形。如图2 所示，△A′BC′即为所求，A′点的坐标为（-4，4）。

She heard a song full of feelings on the radio.（她从收音机里听到了一首充满感情的歌曲。）

（3）直接利用位似图形面积比得出相似比为1∶2，即可得出对应点位置。如图2 所示，△AB2C2即为所求。

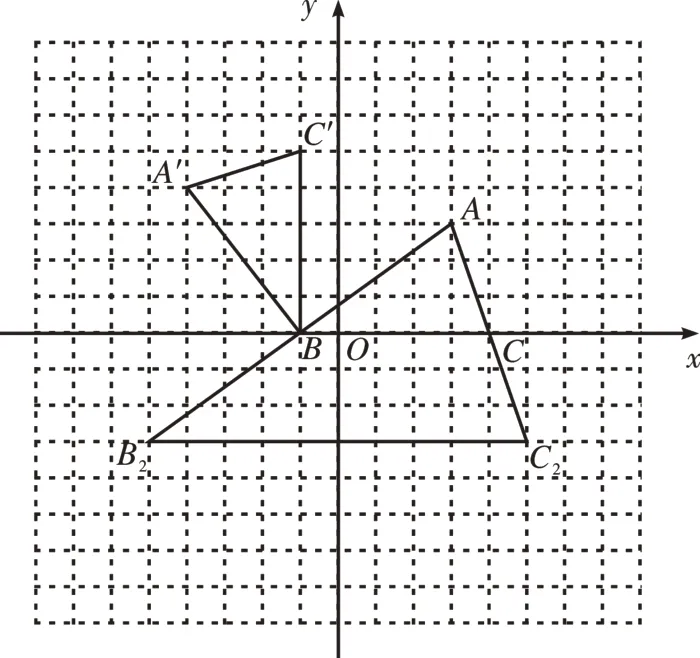
图2

评注：此类题型常需在网格中作图，且有坐标系。在网格中作图要充分利用网格的水平线和竖直线所指的方向，找到图形变化后的对应点。一般图形顶点为格点的，对应点也在格点上，作图时要依靠关键点来控制图形的形状。

二、设计测量方案

对于过高或过宽的物体，或者有障碍物的物体，通常不能直接测量其高度或宽度，对此可以利用所学数学知识设计测量方案，根据易测出的数据算得所求物体的高度或宽度。其中，可利用的数学知识包括全等三角形、三角形的中位线、相似三角形、勾股定理及锐角三角函数。测量工具包括皮尺、测角器、平面镜、标杆等。

［例2］为了测量某电线杆（如图3）的高度，老师给学生准备了如下测量工具：皮尺、标杆、测角仪和平面镜。其中测角仪是用来测量仰角、俯角的仪器。请根据你所设计的测量方案，回答下列问题：（1）请画出你的测量方案示意图，并写出你所选用的测量工具；（2）根据示意图，写出你求电线杆高度的思路。

解析：（1）根据题意，测量方案示意图如图4 所示；选用的测量工具为高1.5 m的测角仪、皮尺。

图3

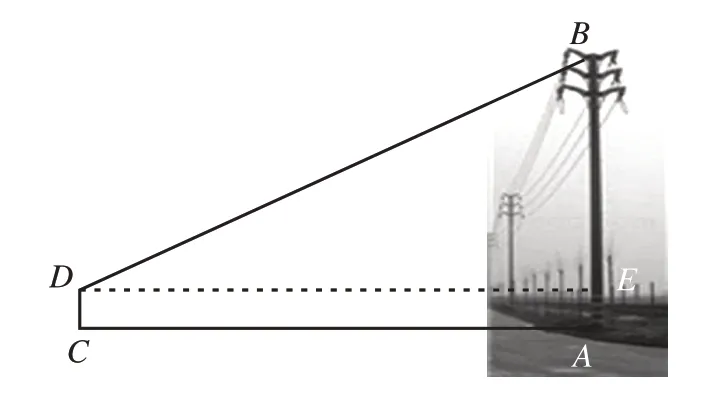
图4

（2）根据正切函数设计测量方案。先测得CA的长度，因为四边形ACDE是矩形，可得DE=CA，AE=CD=1.5；根据正切函数求得BE，AB=BE+1.5，即CA（测角仪离电线杆的距离）=a，CD（测角仪的高）=1.5，∠BDE（测角仪测得的仰角）=α，

根据正切函数得tanα=，因为DE=CA=a，得BE=atanα，则AB=BE+AE=atanα+1.5，故电线杆高度为(atanα+1.5)米。

评注：本题构造的图形是直角三角形和矩形，根据测得的仰角和水平距离，利用锐角三角函数求得电线杆的高度。本题选用正切设计方案是最好的选择，因为构造的直角三角形的斜边也无法测量，所以正弦与余弦都不能选择。

三、按要求剪拼图形

［例3］如图5 所示，把一个三角形沿中位线剪切后，可以得到一个三角形和一个四边形，这两个图形可以拼成平行四边形，仿照上面的方法，完成下面的操作：（1）如图6 所示的平行四边形ABCD，把它剪成两个图形，使这两个图形可以拼成一个矩形，要求在图中画出剪切线；（2）如图7 所示的梯形ABCD，把它剪成两个图形，使这两个图形能拼成一个平行四边形，要求在图中画出剪切线。

图5

图6

图7

解析：（1）因为有一个角是直角的平行四边形是矩形，所以可以考虑通过作高得到一个直角，如图8，过点A作AE⊥BC，垂足为E，再把△ABE剪切下来，移到△DCF的位置；

（2）因为梯形与平行四边形的主要区别是：平行四边形有两组对边分别平行，梯形只有一组对边互相平行。因此，可以考虑作不平行对边的平行线。如图9，过AB的中点G作GF∥DC，再把△BGF剪开，然后旋转到△AEG的位置即可。

评注：本题的剪切线表现出三种形态，分别是中位线、高、平行线。其实还有对角线、对边中点的连线、过中心的直线等，它们都属于一次剪切线，剪切线就是一条折线。本题第（1）小题剪切后得到的△ABE通过平移进行拼接；第（2）小题剪切后得到的△BGF通过旋转进行拼接。当然拼接时也有借助轴对称的。

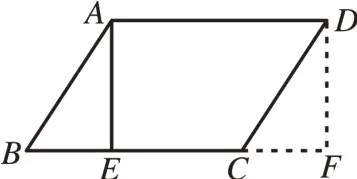
图8

图9

四、通过函数图像解决几何问题

通过观察函数图像获得信息，不仅可以解决实际生活问题，还可以提高学生分析问题和解决问题的能力。用函数图像解决几何问题时，要厘清图像的含义，要有一定的识图技能。

［例4］九（1）班的数学兴趣小组正在探究这样一个问题：如图10，点D是上一动点，弦BC的长为8 cm，取线段BC的中点为点A，过点C作CF∥BD，点F是DA延长线与CF的交点。△DCF为等腰三角形时，线段BD的长度是多少？

兴趣小组的学生发现，此问题不易通过直接推理计算解决，于是尝试通过函数图像研究此问题的答案。请将下面的探究过程补充完整：

图10

（1）当点D在上移动时，线段BD的长不断变化，小组学生分别测量线段BD，CD，FD的长度，得到下表的几组对应值（单位：cm）。

①当点D为的中点 时，上 面表格中a的 值为多少？

②有学生说：“线段CF的长度不用测量就能得到答案。”这种说法对吗？为什么？

（2）兴趣小组的学生将线段BD的长度作为自变量x，把CD和FD的长度作为x的函数，标记为yCD和yFD，其中函数yFD的图像（如图11）兴趣小组的学生已经画出来了，你能在同一坐标系中画出函数yCD的图像吗？

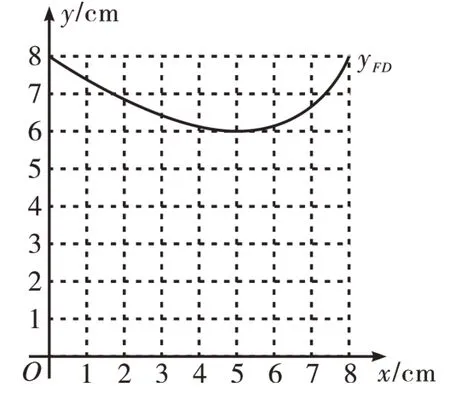
图11

（3）在同一坐标系内根据需要继续画图，结合图像你能看出当△DCF为等腰三角形时，线段BD长度的近似值吗？

分析：（1）①在同圆或等圆中，等弧所对的弦也相等，得a=5.0；②通过“角边角”证明△BAD≌△CAF，可得BD=CF；（2）用描点法画出函数yCD的图像；（3）先画出yCF的图像，那么函数yCD，yFD，yCF的图像彼此的交点的横坐标就是BD的长度。

解：（1）①因为点D为的中点，所以由圆心角定理，得BD=CD=a=5.0；②因为点A是线段BC的中点，所以AB=AC，因为CF∥BD，根据“两直线平行，内错角相等”得∠F=∠BDA，因为∠BAD=∠CAF，得△BAD≌△CAF，所以BD=CF，所以这种说法正确。

（2）根据表格中BD、CD的每组对应值，描出相应的点，再用平滑的曲线画出函数yCD的图像（如图12）。

图12

图13

（3）yCF的图像如图13 所示。△DCF为等腰三角形有以下三种情况：一是CD=FD，二是FD=CF，三是CF=CD。当CD=FD时，则函数yCD与yFD图像的交点的横坐标就是BD的长，由图像可得BD=3.8；当FD=CF时，则函数yFD与yCF图像的交点的横坐标就是BD的长，由图像可得BD=6.2；当CF=CD时，则函数yCD与yCF图像的交点的横坐标就是BD的长，由图像可得BD=5.0。由图像可得：BD的长度为3.8 cm或6.2 cm或5.0 cm时，△DCF为等腰三角形。

评注：本题解决几何图形问题的方法别具一格。本题既考查了等腰三角形的判定，又考查了函数图像交点的意义，体现了数形结合思想。