用两点间的距离公式解题的研究

江苏太仓市良辅中学（215400）王 艳

在考题中，经常遇到平行y轴的直线上的两点之间的距离计算问题，利用两点间的距离公式可计算线段的最值、图形面积的最值、点的坐标等。下面就结合一道考题谈谈两点间的距离公式的具体运用。

一、题目呈现

2022 年北京冬奥会即将召开，激起了人们对冰雪运动的极大热情。如图1 是某跳台滑雪训练场的横截面示意图，取某一位置的水平线为x轴，过跳台终点A作水平线的垂线为y轴，建立平面直角坐标系，图中的抛物线C1：y=+1近似表示滑雪场地上的一座小山坡，某运动员从点O正上方4米处的A点滑出，滑出后沿一段抛物线C2：+bx+c运动。

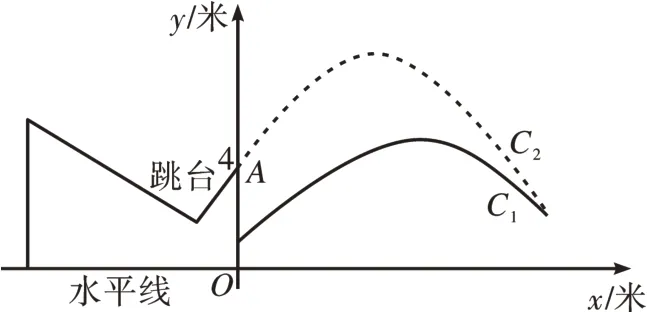
图1

（1）当运动员运动到离A处的水平距离为4 米时，离水平线的高度为8 米，求抛物线C2的函数解析式（不要求写出自变量x的取值范围）；

（2）在（1）的条件下，当运动员运动的水平距离为多少米时，运动员与小山坡的竖直距离为1米？

（3）当运动员运动到坡顶正上方，且与坡顶距离超过3米时，求b的取值范围。

二、题目分析

考题以2022 年北京冬奥会为问题背景，以二次函数为知识基础，以解析式的确定、竖直距离、不等式为问题解决的主渠道，以待定系数法、两点间的距离公式、不等式思想、数形结合思想为主要解题思路，体现“数学源于生活，同时服务生活”，实现学数学、用数学的双向融合。

三、解法探究

四、思考

透过考题，我们得到如下启示：

第一，数学学习夯实基础是关键，如这里的待定系数法，是一种基本方法，解方程组是方法的核心。若是基础不牢，连方程组都不能正确解答，后面的问题就难以解决。

第二，抓住问题的关键。解答时，充分利用函数的解析式，用好“横坐标相同”这一特殊条件，表示点的纵坐标，利用竖直距离等于两点纵坐标差的绝对值建立不等式，也体现了转化思想。

第三，用活各种数学思想是解题的灵魂和指南。

五、变式应用

（一）反比例函数中，求三角形面积的最小值

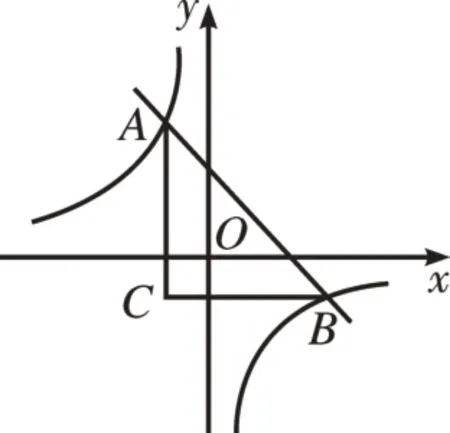
图2

［例1］如图2，直线y=-x+m与双曲线y=-相交于A，B两点，BC∥x轴，AC∥y轴，则△ABC面积的最小值为 。

（二）当线段最长时，求线段和的最小值

［例2］如图3，抛物线y=-x2+bx+c与x轴 交于A、B两点，与y轴交于点C，直线y=-x+2 过B、C两点，连接AC。

图3

（1）求抛物线的解析式；

（2）求证：△AOC∽△ACB；

（3）点M(3,2)是抛物线上的一点，点D为抛物线上位于直线BC上方的一点，过点D作DE⊥x轴交直线BC于点E，点P为抛物线对称轴上一动点，当线段DE的长度最大时，求PD+PM的最小值。

（三）当三角形的面积最大时，求倍数线段和的最小值

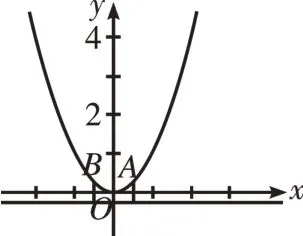
图4

［例3］已知抛物线C1：y=ax2的图像如图4。直线l：y=点B为抛物线上的任意一点且满足点B到点A的距离与点B到直线l的距离始终相等。

（1）直接写出：a的值______；

（2）如图5，若直线l2：y=mx+交抛物线于D、E两点（点D在点E的右边），交x轴于点F，过点E作EM⊥l于点M，过点D作DN⊥l于N，点H为MN的中点，若点H到直线l2的距离为，求m的值；

图5

（3）如图6，将抛物线C1向右平移2 个单位，向下平移1个单位得到抛物线C2，C2交x轴于A、B两点，交y轴于点C，点P为直线BC下方抛物线上一点，点Q为y轴上一点，当△PBC的面积最大时，求2PQ+CQ的最小值。

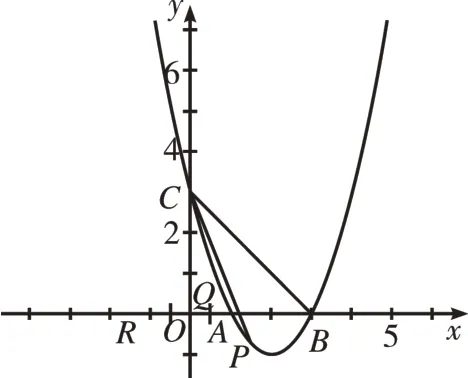
图6

图7

（2）如图7，连接EH并延长交DN延长线于点G，连接AH，DH，∵∠EMH=∠GNH=90°，∠EHM=∠GHN，MH=NH，∴△EMH≌△GNH，∴EH=GH，EM=GN，∵EA=EM，DA=DN，∴ED=EA+DA=EM+DN=DG，∴∠EDH=∠GDH，DH⊥EG，∴△ADH≌△NDH(SAS)，∴∠HAD=∠HND=90°，∴AH=

（3）∵抛物线C1向右平移2个单位，向下平移1个单位得到抛物线C2，∴C2的解析式为y=(x-2)2-1，即y=x2-4x+3，令y=0，得(x-2)2-1=0，解得x1=1，x2=3，∴A(1,0)，B(3,0)，令x=0，得y=3，∴C(0,3)，

设直线BC的解析式为y=kx+3，∴3k+3=0，即k=-1，∴直线BC的解析式为y=-x+3，

如图8，连接PB，PC，作直线BC，过点P作PW⊥x轴，交直线BC于点W，设点P的横坐标为x，则P(x,x2-4x+3)，W(x,-x+3)，∴WP=-x+3 -(x2-4x+3)=-x2+3x，∴S△PBC=

图8

点评：本题考查了抛物线的解析式、抛物线的最值、抛物线与一元二次方程的关系、三角函数、勾股定理、等腰三角形的性质和判定、全等三角形和垂线段最短。熟练掌握抛物线解析式的确定，三角函数性质，线段和的最值求法是解题的关键。