球磨机振动信号多传感器融合特征维数约简*
姜志宏, 刘民民, 胡 博, 卢文海
(1.江西理工大学 机电工程学院,江西 赣州 341000; 2.江西省矿冶机电工程研究中心,江西 赣州341000)
0 引 言
信号的特征提取作为机械设备负荷识别及工作状态参数预测的关键环节,旨在借助各种信号处理方法构造出能够表征设备状态信息的特征量[1]。但是,不同特征量组成高维特征集为后续模式识别与智能预测环节提供充足数据来源的同时,增加了计算负担,降低了识别效率。因此,在保留原始信号中大部分本征信息的前提下,提取出高维特征集的低维表达形式的维数约简方法应运而生[2]。早期的特征约简方法主要有主成分分析(PCA)、多维尺度分析[3]以及线性判别分析[4]等。近年来兴起的流形学习方法[5]被广泛运用于人脸识别、图像处理等领域的非线性特征约简中,机械设备工作状态预测过程也逐渐选用此类方法进行特征降维。
球磨机多传感器特征层“特征—特征”信息融合,其实质上属于一类特殊的特征维数约简问题,因此,采用的信息融合算法以特征降维算法为主,并辅以其他类型的特征维数参量二次整合与优化,共同完成多传感器信息的特征层融合[6,7]。王恒等人[8]基于最小二乘支持向量机(LS-SVM)算法提出一种基于多传感器信息融合的球磨机料位测控系统,实现球磨机的矿料位置检测。孙卫祥[9]采用主成分分析方法对来自于多个传感器的转子故障特征集进行特征融合,从而在特征融合的同时实现特征约简。
本文以二阶张量作为球磨机筒体振动信号特征融合表现形式,并对传统张量局部保持投影(tensor partial preservation projection,TPPP)算法进行改进,将特征样本的几何结构信息与类别信息加入至相似性加权矩阵的计算过程中,提出一种基于集成矩阵距离测度的监督二阶张量局部保持投影(supervised second-order tensor local preservation projection,SSTLPP-IMDM)算法,最后将该方法运用于球磨机筒体振动信号特征维数约简中,从而验证该方法的有效性和优越性。
1 基本理论
1.1 传统二阶张量局部保持投影算法
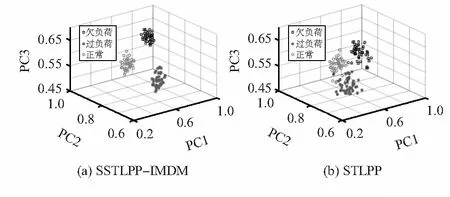
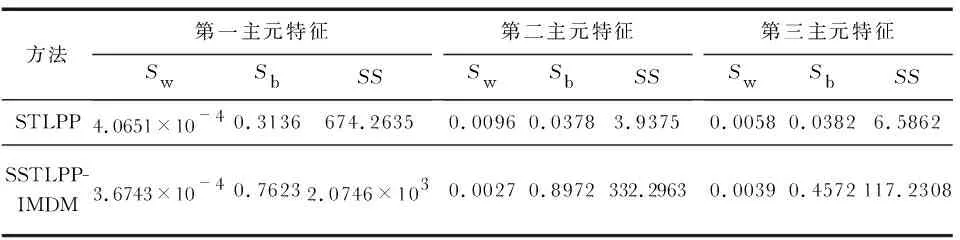
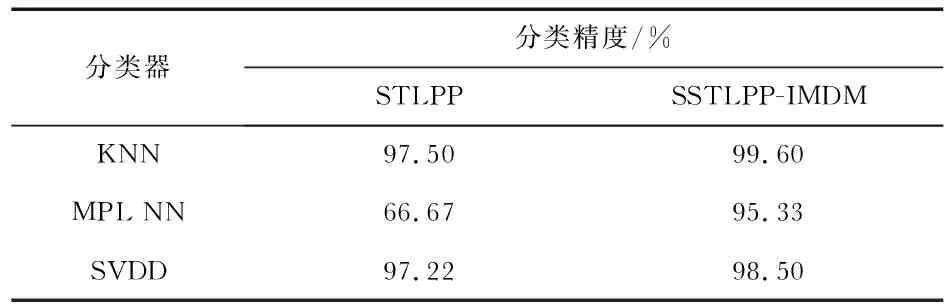
二阶张量局部保持投影(second-order tensor local pre-servation projection,STLPP)算法的原理为:设有N个二阶张量表达形式的特征样本为X={X1,X2,…,XN}∈Rn×m,通过式(1),从而获得两个变换矩阵U∈Rn×n′及V∈Rm×m′(n′,m′ (1) 式中 ‖‖F为矩阵的Frobenius范数。Sij为近邻图G的权矩阵S中第i行第j列的元素;D为对角矩阵,Dii=∑jSij。 通过式(2)迭代推导,计算出其广义特征向量,并求出最优U和V (2) 最终,可将原始二阶张量形式的高维空间特征投影至低维空间,即,Yi=UTXiV。其中,Yi为相比于Xi维数更低的二阶张量。 由式(1)可知,求解近邻图G的加权矩阵S的方法存在一定的不足之处,其忽略了特征样本数据中各个元素之间的空间信息,最终将出现不同样本间的相互匹配性能较差的问题。因此,传统的STLPP算法对分类环节中的类别信息未得到有效运用。 集成矩阵距离测度(IMDM)准则旨在求得两个二阶张量表达形式特征样本之间的距离。设任意两个二阶张量表达形式的特征样本为A=[a1,…,ah,…,am]T与B=[b1,…,bh,…,bm]T,其中ah=[a1h,…,alh,…,anh]T,bh=[b1h,…,blh,…,bnh]T,基于IMDM准则的样本间距离计算公式为 =‖[‖a1-b1‖2,…,‖ah-bh‖2,…, ‖am-bm‖2]T‖p (3) 式中p为可变量,用于表现距离函数对后续模式识别能力的影响程度。当p>1时, ‖ah-bh‖2越大对dist(A,B)的影响越大;当p≤1时, ‖ah-bh‖2越小对dist(A,B)的影响越大。由于dist(A,B)最终运用于模式识别中各个特征样本间类别评定,因此,应选用较小值的‖ah-bh‖2对dist(A,B)的影响能够大于较大值的‖ah-bh‖2,这表明两个向量ah与bh的匹配度更高。因此,为精确计算特征样本间距离,应取p值为0 针对传统STLPP算法运用Frobenius范数计算样本数据之间的距离存在弊端,结合集成矩阵距离测度准则,提出一种基于SSTLPP-IMDM的算法。 将投影空间上样本矩阵距离及相似性加权矩阵计算上的改进运用于传统STLPP算法中,其变换矩阵U与V的求解转变公式为 (4) 式中DDii为特征样本集Xi与Xj间的近邻程度,投影张量空间里的两个投影点Yi=UTXiV与Yj=UTXjV之间距离使用IMDM准则进行计算。 为了研究磨机筒体振动信号与磨机负荷状态及其工作状态参数之间的关系,选用φ330 mm×330 mm的Bond指数实验球磨机进行磨矿实验。实验中使用的物料为钨矿石,其密度为1 800 kg/m3。由于实际磨矿过程中,物料的入料粒度存在差距,因此,参考工业中小型球磨机的入料粒度,将矿石粒度筛分为5个等级,分别为2~5,5~8,8~11,11~15,15~20 mm。筒体内物料的破碎与研磨主要依靠钢球对其做功,而钢球的大小不同在磨矿作业中破碎作用也不相同。为了提高球磨机的磨矿的效果,选用φ20 mm,φ30 mm,φ40 mm,φ50 mm的钢球进行实验,其密度为7 800 kg/m3。在球磨机筒体外冲击区和拋落区各安装1只传感器。结合本课题组现有实验条件搭建实验平台,球磨机筒体振动信号采集系统实验平台如图1所示。 图1 球磨机振动信号采集系统实验平台 磨矿实验以填充率、料球比和转速作为变量,采用单因素全组合实验方案。其中,填充率分别为0.2,0.3,0.4,0.5,料球比分别为0.5,0.6,0.7,0.8,0.9,1.0,1.1和1.2,转速分别为40,50,60 r/min,一共包括96组实验。 根据文献[10]提出的方法,求解出磨机筒体振动信号的最大频率为3 880 Hz,由于采样定理指出,采样频率应大于信号最高频率的2倍,但在实际工程应用过程中,一般要将采样频率设置为信号最高频率的5~10倍,才能较为准确地采集到实际信号[11]。为了提高信号的频率分辨率,在满足信号能够精准采样的前提下一般选用较小的采样频率,因此,本研究中将采样频率设置为fs=20 000 Hz。 进行筒体振动信号采集,得到筒体振动信号的时域波形,发现相同球磨机工况下抛落区与冲击区加速度传感器采集得到的振动信号各不相同,由此表明球磨机筒体不同位置的振动信号具有明显不同的设备状态表征特性。因此,将来自于多只传感器的球磨机筒体振动信号特征进行融合,为球磨机负荷状态识别提供一种有效方法。 针对不同负荷状态下采集得到的磨机筒体振动信号的样本数据,分别提取8个时域特征参量和5个频谱特征参量[12]:均值、方差、方根幅值、有效值、峰值、偏度指标、峭度指标、峰值因子、均值频率、标准偏差频率、频谱偏度、频谱峭度、重心频率;两个熵值特征参量:样本熵、模糊熵。将以上15个特征参量作为特征约简的原始高维特征集。 基于SSTLPP-IMDM算法的球磨机筒体振动信号多传感器特征维数约简的具体实施流程如图2所示。 图2 球磨机振动信号多传感器融合特征维数约简 由于后续需要对降维特征集的分类性能进行评判,因此,需要设定训练样本和测试样本。实验中提取出100组球磨机来自于拋落区与冲击区2只加速度传感器的筒体振动信号,由此,可得到一个2×15×300维的特征集样本张量X。特征样本中50组特征样本集作为球磨机负荷识别模型的训练样本,剩余50组则作为模型的测试样本,因此,该特征样本张量X中含有一个2×15×300维的训练样本张量X1及一个2×15×300维的测试样本张量X2。根据图2中描述的流程,将上述设定的特征集训练样本张量X1作为输入,从而获得相应的变换矩阵U和V,最后求解出其低维投影张量Y1∈Rn′×m′×150,即得到高维特征样本集降维后的特征集。 为了可视化表现出磨机筒体振动信号特征降维效果,将降维得到的低维投影样本张量Y1中的各特征样本数据矩阵向量化,从而得到基于SSTLPP-IMDM算法降维后向量化表达的三维散点分布效果如图3(a)所示。将基于传统STLPP算法的维数约简方法运用于同一训练样本张量X1中,其降维得到的低维投影样本张量Y′1的向量形式的三维散点表现形式如图3(b)所示。 图3 基于SSTLPP-IMDM和STLPP算法的训练样本张量维数约简后特征集的散点分布 将图3(a)与图3(b)进行对比可知,图3(b)中运用传统STLPP算法维数约简后的特征样本集在不同类别的样本分布中存在的混合现象,即不同类别的样本特征集区分度不高;而运用SSTLPP-IMDM 算法维数约简后的特征样本集在不同类别中区分度较高,即同类样本相互之间分布紧凑,不同类样本之间具有明显分离。上述实验结果表明,基于SSTLPP-IMDM算法的维数约简方法能够有效地将原始高维二阶张量形式的特征样本集投影至低维特征样本集中,且其分类性能明显优于传统的STLPP算法。 由于上述实验是针对不同维数约简方法,从定性的角度衡量降维后特征集的聚类特性[13],引入特征聚类性能指标对各类算法的降维效果进行定量评价,即类内散度Sw、类间散度Sb以及类内—类间综合散度SS。其计算公式为 (5) (6) (7) 由式(5)~式(7)可知,类内散度Sw表示在同一类别中,各个样本之间的平均聚集程度;类间散度Sb表示在不同类别中,各个样本之间的平均分离程度;类内—类间综合散度SS则表示Sw与Sb的综合评价结果。STLPP和SSTLPP-IMDM维数约简方法降维后各特征集之间的聚类评价指标计算结果如表1所示。 表1 不同维数约简方法降维后各特征集之间的聚类评价指标计算结果 由表1分析可知,在对球磨机筒体振动信号特征降维过程中,运用SSTLPP-IMDM的维数约简方法降维后的样本特征集的类内散度Sw均小于SSTLPP维数约简方法、类间散度Sb均大于SSTLPP维数约简方法,且其聚类综合评价指标SS的结果也相比SSTLPP降维方法明显更大,这表明,基于SSTLPP-IMDM算法的球磨机筒体振动信号特征维数约简方法能够到达更好的聚类效果。 为进一步验证SSTLPP-IMDM算法的优越性,采用三种典型分类器模型:K最近邻(KNN)分类算法、多层感知神经网络(MLP neural network)模型及支持向量数据描述(SVDD)模型对SSTLPP和SSTLPP-IMDM维数约简方法降维特征集的分类精度进行对比分析。将维数约简后的低维特征样本在上述3种分类模型中各进行10次分类实验,取10次实验的分类精度均值作为最终结果。经过STLPP和SSTLPP-IMDM维数约简方法得到的降维特征集在3种典型分类模型中的分类精度如表2所示。 表2 STLPP和SSTLPP-IMDM维数约简方法在3种典型分类模型中的分类精度 由表2可知,基于SSTLPP-IMDM算法的张量形式表达多传感器融合特征样本数据的降维特征集相比STLPP降维特征集具有更高的分类精度,其分类精度分别为99.6 %,95.33 %, 98.5 %,因此,实验结果再一次验证了本文研究提出的基于SSTLPP-IMDM的维数约简算法结合张量形式表达的多传感器特征信息融合能够在增加特征集有用信息的同时提高其类别分类精度。 提出了SSTLPP-IMDM算法,并将该方法运用于球磨机筒体振动信号特征维数约简中,通过对传统STLPP算法中样本矩阵距离及相似性加权矩阵计算方法进行改进,实现了二阶张量形式表达的多传感器特征维数约简。相比传统的STLPP降维算法,SSTLPP-IMDM算法具有更好的聚类特性且能够有效提高分类模型的分类精度。通过对来自2只定位于球磨机筒体抛落区和冲击区的加速度传感器采集到的实验数据进行分析验证,表明了基于SSTLPP-IMDM算法在球磨机筒体振动信号特征融合维数约简中的技术优势,提高了后续球磨机内部负荷状态识别的可靠性。
1.2 SSTLPP算法改进
2 实验验证
2.1 实验平台的搭建

2.2 实验方案设计
2.3 实验数据获取与预处理
3 基于SSTLPP-IMDM算法的球磨机振动信号特征维数约简
3.1 多传感器融合特征维数约简步骤

3.2 降维效果的验证与对比
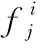
3.3 降维特征集的分类性能验证与对比
4 结 论

