耐高温压力—振动复合传感器设计与仿真*

孙博山, 熊继军, 李 晨

(1.电子测试国防科技重点实验室,山西 太原 030051；2.中北大学 仪器科学与动态测试教育部重点实验室，山西 太原 030051)

0 引 言

近年来，在航空领域，如航空发动机中工作在高温恶劣环境内的压气机、燃烧室、涡轮叶片等关键部件对压力及振动参数的高精度获取提出了更高的要求[1,2]。超高温恶劣环境极易引起压力及振动传感器的工作失准、失效甚至损坏。因此，研究一种可在高温环境中可靠且稳定工作的压力及振动复合传感器具有极其重要的使用价值。

目前，研究人员们对基于电阻应变式[3]、压电式[4]、电容式[5]、光纤式[6]等原理的耐高温压力传感器及振动传感器展开了深入的研究。例如，2016年，Yao Z等人[7]提出了一种基于压阻式测量原理的绝缘体上硅(silicon on insulator,SOI)压力传感器，能够实现-50～220 ℃温度范围内的压力测量。2018年，Liang H等人[8]设计了一种无膜片的光纤法珀干涉式压力传感器，可以测量800 ℃温度范围内压力的变化。2011年，Kim K等人[9]利用YCOB(YCa4O(BO3)3)单晶的压电转换原理制备出可应用在1 000 ℃高温环境中的振动传感器。2022年，Qian J等人[10]制备并测试了基于光纤法珀原理的高温振动传感器，能够实现20～400 ℃环境中振动参数的测量，最大非线性误差为1.88 %。但在实际的工程化应用中，狭小受限空间对传感器的体积大小及多功能性具有及其突出的需求，高效的多参数复合传感器已成为前沿研究方向。

本文提出了一种基于高温陶瓷共烧(high temperature co-firing ceramic,HTCC)工艺的应用于高温环境下的压力—振动复合测量传感器，设计了独特的压力—振动复合传感器结构及制备方法，利用Ansys Workbench仿真分析了薄膜厚度、悬臂梁长宽比、质量块重量及温度等对传感器灵敏度及固有频率的影响，分析传感器静态及动态性能并优化结构参数。

1 压力—振动复合传感器结构参数

1.1 结构设计

本文选用Al2O3陶瓷[11]作为传感器基底材料，铂作为功能材料，HTCC传感器结构主要由振动敏感电容、压力敏感电容、碳膜及5层生瓷片组成，设计的传感器分层结构如图1所示。选用的HTCC工艺包括生瓷片打孔、铂浆料的丝网印刷、填充易逝碳膜、生瓷片层压及高温烧结。其中，易逝碳膜的填充能够避免生瓷片在高温烧结过程中因重力作用而发生坍塌。

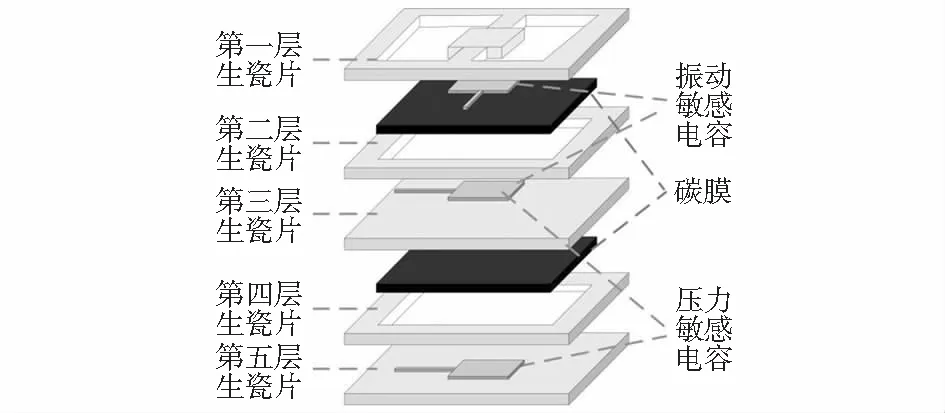
图1 压力—振动复合传感器分层结构

1.2 参数分析

1.2.1 压力敏感结构参数

压力敏感结构设计为弹性薄板腔结构，薄板的弹性变形和腔体的气密性是压敏芯片正常工作的必要条件。当外部空气压力大于腔体内部空气压力时，弹性薄板向空腔内弯曲变形。腔体上视图为边长为Lp的正方形，空腔高度为dc。根据经典薄板理论，当在薄板表面均匀施加压力时，薄板的抗弯刚度可计算为

(1)

式中E为薄板的杨氏模量，ν为薄板的泊松比，薄板厚度为dw。当施加均匀压力P时，薄板中心产生的最大挠度d0可表示为

(2)

无压力时，初始电容为

(3)

式中ε0为真空介电常数，εr为弹性薄板材料的相对介电常数。当施加压力P时，上下板发生弹性变形，板与板之间的距离发生变化。在此条件下[12]，工作电容可表示为

(4)

通过MATLAB软件分析膜片厚度(100～300 μm)、空腔边长(1.5～3 cm)与空腔高度(150～300 μm)对压力传感器挠度及电容变化量的影响，仿真结果如图2所示。可以看出：压力传感器的膜片最大挠度及电容变化量与膜片厚度呈反比，膜片最大挠度与空腔边长呈正比，压力传感器的电容变化量与空腔高度呈反比。

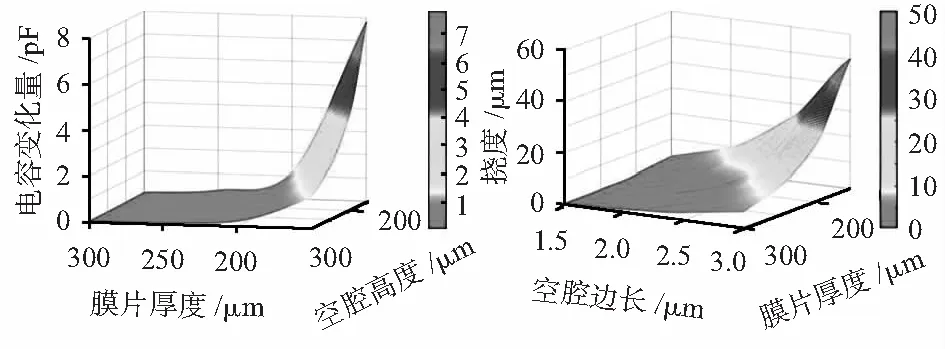
图2 MATLAB仿真膜片厚度、空腔边长及高度对压力敏感结构的性能影响

1.2.2 振动敏感结构参数

振动敏感结构为双端固支梁—质量块结构。依靠质量块上的电容的可动极板感知环境中的振动参数。未受力的情况下,电容初始值为

(5)

式中AL为电容极板间的正对面积，d0为极板间距离。当环境中振动参数发生变化时，极板间距离发生变化，电容值随之变化，根据力学模型，在负载加速度a时，振动敏感结构挠度可表示为

(6)

式中E为Al2O3陶瓷的弹性模量；l、h、w分别为梁的长度、宽度和厚度，m为质量块的质量。此时，变化的电容值为

(7)

此外，在振动过程中，悬臂梁的尺寸直接影响着结构的稳定性，引用固有频率F、最大应力Tmax及最大应变Zmax对结构稳定性及可靠性进行表征[13]，三者的表达式为

(8)

(9)

(10)

通过MATLAB软件分析梁长与梁宽对振动敏感结构固有频率、挠度、最大应力及应变的影响，设置梁长在13～16 mm间变化，梁宽在3～4.5 mm间变化，绘制相关曲线如图3所示。从图中可以看出，振动敏感结构的挠度、最大应力及最大应变与梁长呈正比，与梁宽呈反比；振动敏感结构的固有频率与梁长呈反比，与梁宽呈正比。

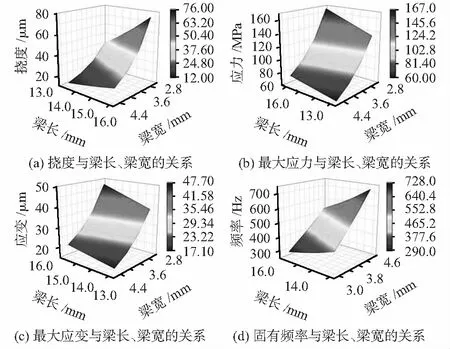
图3 MATLAB仿真梁尺寸对振动敏感结构的性能影响

综合考虑压力—振动敏感结构性能、制备工艺等影响因素，最终设计的压力—振动复合传感器结构尺寸参数设置：压敏膜片厚度dw为200 μm，空腔边长Lp为25 mm,空腔高度dc为200 μm,梁长l为15 mm，梁宽h为4.5 mm,梁厚w为200 μm,质量块尺寸为10 mm×10 mm×1 mm，电容极板面积AL为100 mm2，电容极板间距离d0为200 μm。

2 仿真分析

参照以上设计的复合传感器结构参数，通过采用有限元分析软件Ansys Workbench对复合敏感结构进行仿真分析，主要包括常温环境下敏感结构的静态分析、模态分析、谐响应分析以及高温环境下的热学分析，以此保证结构设计的合理性，仿真过程中所需的基底材料氧化铝陶瓷的基本参数:抗弯强度为650 MPa,热导率为26 W·m-1·K-1,泊松比为0.22,杨氏模量为340 GPa，密度为3.89 g/cm3,热膨胀系数为6×10-6·℃-1,介电常数为9.9,烧结温度为1 500 ℃。

2.1 复合敏感结构的静态分析

在压力敏感结构的敏感膜表面施加均匀的0.5 MPa的压力，在振动敏感结构的质量块上施加25gn载荷的加速度，复合敏感结构载荷作用下的位移及等效应力仿真结果如图4所示。

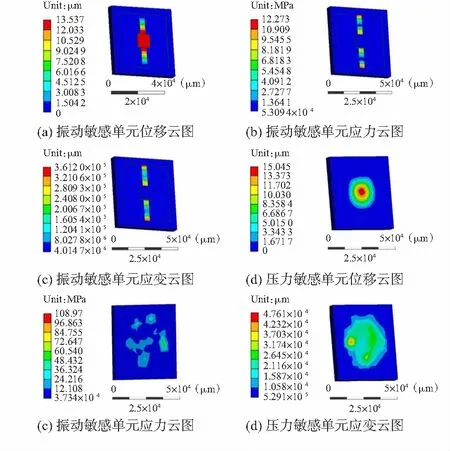
图4 常温环境下压力—振动复合传感器的静态分析

从图4可以看出，对结构施加固定载荷后，最大形变均出现在结构正中心，压力敏感结构和振动敏感结构的最大形变分别为15.045，13.537 μm。压力敏感结构的最大等效应力出现在空腔边缘，其值为108.97 MPa。振动敏感结构的最大等效应力出现在边框与梁的连接处及质量块与梁的连接处，其值为12.273 MPa。因此，在施加载荷的情况下，压敏膜片边缘及梁的连接处易发生断裂而使得结构失效。氧化铝陶瓷材料的抗弯强度为650 MPa，依据最大许用应力计算公式σmax=σ/η(设定安全系数η为1.5)，得到最大许用应力为433 MPa，远大于0.5 MPa均匀压力及25gn载荷下的等效应力。压力敏感结构的最大形变量小于敏感膜厚度的1/6，符合小挠度计算要求，且最大等效应力小于最大许用应力，因此，复合敏感结构可实现0～0.5 MPa下的压力测量。

2.2 复合敏感结构的模态分析

为避免工作过程中因过载及共振等现象引起结构断裂失效。如图5所示，对复合敏感结构进行了4阶模态分析，一阶模态为敏感结构工作模态，二、三、四阶模态为干扰模态。可以看出，复合敏感结构的一阶模态频率为701.44 Hz，二、三、四阶模态频率分别为1 495.6,2 600.2,9 794.6 Hz，发现复合敏感结构的二、三、四阶模态频率超过一阶模态频率的2倍以上，说明复合敏感结构具有良好的抗干扰能力。

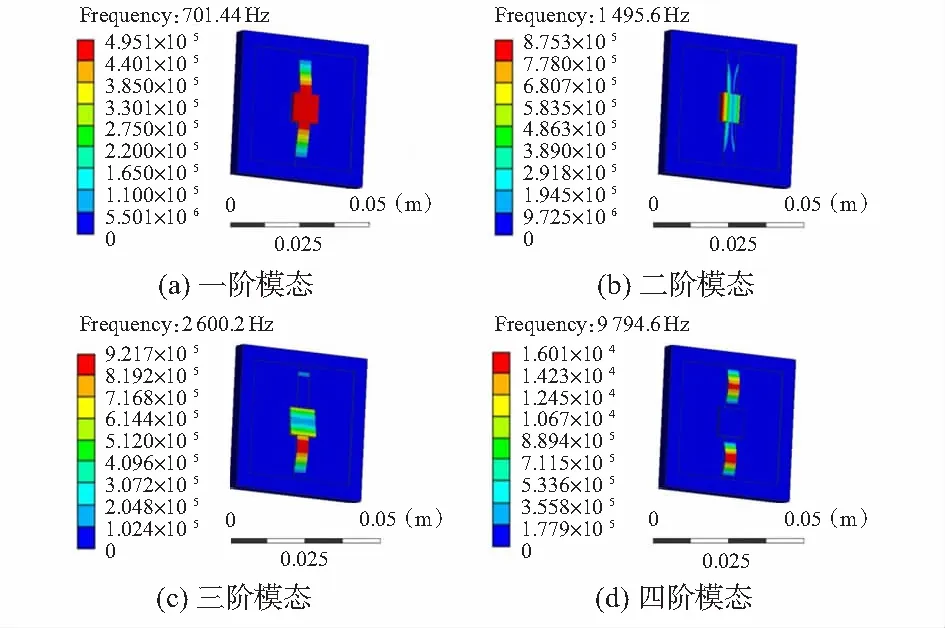
图5 压力振动复合传感器的模态分析云图

为得到结构在施加周期性载荷的情况下周期性响应，250～1 450 Hz扫频范围内敏感结构的谐响应分析如图6所示，可以看出，敏感结构的稳态响应只有一个峰值(700.83 Hz)，且与一阶模态的工作频率大致相同(701.44 Hz)。因此，复合传感器可实现116.90～233.81 Hz频率的振动测量，并且具有较强稳定性和抗干扰能力。

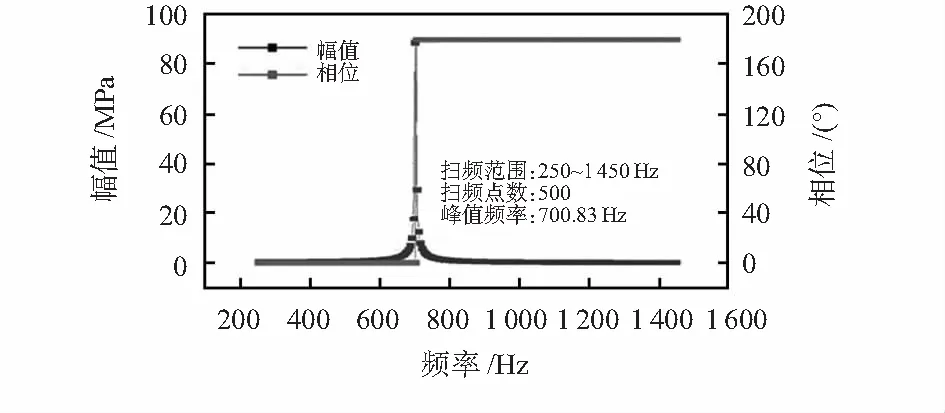
图6 压力—振动复合传感器的谐响应分析

2.3 复合敏感结构的热力学分析

本文仿真了固定载荷下复合敏感结构在23，400，800，1 200 ℃下的位移云图，如图7所示。可以看出，随着温度的升高，复合敏感结构的挠度不断增大，这是由于基底材料氧化铝陶瓷的机械性能在高温环境中发生变化，主要为材料的杨氏模量随温度升高而下降。

图7 不同温度下压力—振动复合传感器位移云图

提取敏感结构在各个温度段下的挠度变化，结合薄膜与振动梁应变电容计算公式，绘制出不同温度下压力敏感结构,在0～0.5 MPa均匀压力负载下的电容—压力变化曲线与振动敏感结构在0～25gn载荷下,电容—加速度变化曲线及其各温度下的灵敏度，如图8所示。

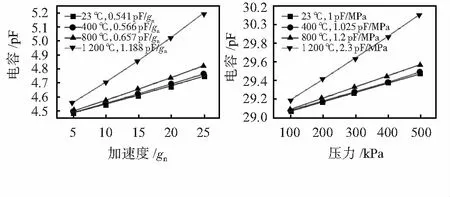
图8 23～1 200 ℃传感器输出电容值随压力与加速度的变化

从图8中可以看出，在固定温度下，压力敏感电容及振动敏感电容随压力或加速度的升高而线性增大，但在固定压力及加速度载荷下，电容随温度的升高而增大，这是由于高温环境下氧化铝陶瓷的杨氏模量及抗弯强度等参数发生变化，使得敏感结构相比常温环境中相同的载荷下挠度变大，进而导致电容极板极间距变小，最终使得压力—振动复合传感器随温度升高而敏感电容值且灵敏度增大。

3 结 论

本文提出了一种基于HTCC技术的耐高温压力—振动复合传感器，可用于23～1 200 ℃高温环境下同时测量压力及振动参数。借助MATLAB仿真软件对敏感结构的敏感膜、质量块及梁的尺寸进行合理化分析。通过Ansys Workbench 有限元分析软件对压力—振动复合传感器在0.5 MPa均匀压力载荷及25gn加速度载荷下的静态力学特性进行仿真分析，结果表明等效应力远小于材料许用应力，故传感器可在设计载荷下正常工作。并对复合敏感结构的动力学特性进行分析，结果表明,传感器具有较高的高频抗干扰能力。最后，对敏感结构在23～1 200 ℃温度下的热力学参数进行分析，结果表明,在相同的压力及振动载荷下，敏感结构的电容输出值及灵敏度随温度升高而增大。