BDS/GPS/GLONASS中长基线解算性能对比分析

闵 阳,冯 威,曹成度,滕焕乐,马 俊

(1.中铁第四勘察设计院集团有限公司,武汉 430063； 2.西南交通大学地球科学与环境工程学院,成都 611756)

我国北斗三号全球卫星导航系统已于2020年7月正式开通。目前，新一代北斗系统包含正常工作卫星44颗，其中3种类型轨道的设计有利于实现星座的更好覆盖，在亚太地区优势更为明显。我国可见BDS卫星数单日均值可达16颗，PDOP均值达到1.66，明显优于GPS，基于BDS单系统观测已能够达到毫米级定位精度[1]。其他导航卫星系统也正处于快速发展时期，多系统组合已成为卫星导航定位技术发展的必然趋势，多系统组合增加了可用卫星数和有效观测量，优化了卫星星座构型。此外，多星座组合可以提升在有遮挡和干扰情况下的定位效果，削弱对单一导航系统的过度依赖，有利于及时识别和剔除故障卫星，提高定位精度和可靠性[2-3]。多系统组合定位得到了学者的高度重视，文献[4-7]研究了多系统兼容与互操作、时空基准统一等基本问题，文献[8-9]进行了GPS/BDS双系统融合定位方法及性能的分析，文献[10-11]针对GPS/GLONASS双系统组合在精密定位中的应用展开研究，也有学者对GPS/BDS/GLONASS、GPS/BDS/Galileo三系统组合以及GPS/BDS/GLONASS/Galileo四系统组合定位中的关键问题进行了探讨[12-14]。

基线解算过程中需要对每颗卫星的观测值进行定权，利用随机模型刻画函数无法表达的残余误差，选择合理的定权方法对于保证基线精度十分关键[15-17]。EUELER首次提出了基于卫星高度角的定权策略[18]，HARTINGER提出基于信噪比的sigma-ɛ模型的定权方法[19]，文献[20]利用Helmert方差分量估计为GPS/BDS组合单点定位观测值定权，文献[21]提出了一种迭代、序贯处理观测序列异方差和时相关序列的GPS随机模型建模方案，文献[22-23]研究了针对不同类型北斗卫星观测值的定权方法，文献[24]提出一种基于PDOP的观测值定权方法，文献[25]则系统介绍了GNSS随机模型估计理论与方法。在多系统组合定位中，由于来自各系统的观测值质量不同，合理定权在保证定位精度和稳定性方面变得更为重要。文献[2，26]研究了GPS/BDS双系统组合定位权比估计方法，文献[12]针对GPS/BDS/GLONASS三系统组合定位的定权问题进行了讨论。随着北斗三代系统正式全面启用，我国及周边地区的北斗卫星观测数量和空间分布发生了显著变化，因此，有必要对当前卫星观测条件下不同系统组合、不同定权方法及不同观测时长下基线定位性能重新进行试验分析和评估。

针对BDS/GPS/GLONASS多系统组合基线高精度快速解算，首先分析多系统组合基线解算函数模型；然后介绍了3种常用基线观测值先验定权方法：等权法、高度角定权法、信噪比定权法。基于融合北斗三代的新一代全星座观测数据，通过试验对比不同系统组合、不同定权方法及不同观测时长的基线解算性能。

1 多系统基线解算函数模型

以BDS/GPS/GLONASS三系统组合中长基线为例介绍基线解算函数模型。各导航卫星系统采用的时间系统和坐标系统不同，因此时空基准统一是多系统融合定位的基本要求[5]。

由于中长基线两端测站的大气延迟误差相关性较弱，双差方程无法直接消除大气延迟误差，通常采用无电离层组合构建函数模型，并对对流层延迟进行参数估计。BDS/GPS/GLONASS三系统的双差无电离层组合方程见式(1)～式(3)。

(1)

(2)

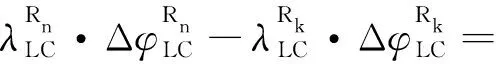
(3)

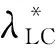
无电离层组合破坏了整周模糊度的整数特性，无法直接固定模糊度，常利用波长较长的宽巷组合，优先固定宽巷模糊度，而后将宽巷模糊度代入无电离层组合观测值求解基频模糊度浮点解，并利用LAMBDA算法得到基频模糊度固定解。将整周模糊度固定解回代到误差方程，即可求得准确的基线向量解[8]。

BDS/GPS/GLONASS三系统观测误差方程为

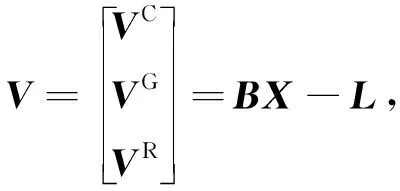
(4)

其中

2 多系统基线观测值先验定权方法

在基线解算过程中，随机模型反映观测数据质量和噪声特性，随机模型设置不合理使得观测值定权不当，从而导致未知参数的最优估计有偏，降低基线解算精度。多系统组合基线解算中，各系统在定义、卫星轨道、信号结构、星历精度等方面都存在差异，导致定位精度不同，定权方法的选取对高精度定位更为关键。重点研究3种先验定权方法：等权法、高度角定权法、信噪比定权法，在不同策略快速基线解算中的适用性。

2.1 等权法

等权法认为来自不同系统的各卫星对应载波相位观测值精度相等且相互独立，单颗卫星观测值方差表示如下

(5)

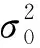
等权法的优点是数据处理简单，但由于忽略了不同卫星之间的精度差异，导致基线解算精度较低，无法满足高精度定位的需要。

2.2 高度角定权法

卫星高度角是评价观测值质量的重要指标，高度角越低，相位观测量受大气误差和多路径效应的不利影响越大，基于高度角对观测值定权可有效提高基线解算精度，其中较为常用的是正弦函数模型，如式(6)所示[27-30]

(6)

式中，a、b为常数项；elv为卫星高度角。

文献[15,31]给出了GPS高度角定权模型中参数的经验值：a=4 mm，b=3 mm。文献[12]通过Helmert验后方差分量估计，得到结论：GPS、BDS、GLONASS相位观测值精度相当，由此认为BDS、GLONASS卫星高度角定权模型参数取值与GPS一致。

2.3 信噪比定权法

信噪比(Signal Noise Ratio， SNR)是指接收机接收到的信号强度与噪声强度的比值，可以反映大气延迟、多路径效应等误差，用以表征观测值质量，常利用载噪比C/N0来表示。基于信噪比的定权模型可表示为

(7)

式中，Ci为与相位跟踪环带宽相关的常数，取1.61×104mm2[32]。信噪比定权法能够更好地表征观测信号精度，因此在软件中得到广泛应用。

3 试验分析

基于我国新一代BDS-3全星座卫星观测条件，针对BDS、GPS、GLONASS不同系统组合，等权法、高度角定权法、信噪比定权法3种先验定权方法，0.5，1，2，3 h四种观测时长，设置不同观测策略，展开基线解算试验分析。通过对比试验，验证BDS-3单系统的定位精度，以及BDS-3对多系统组合定位精度的改善效果，分析不同定权方法的适用性及不同观测时长下基线解算性能的规律。

3.1 数据介绍

试验选取某高速铁路框架网长度为65.9 km的基线，观测时间为2020年11月7日全天24 h，采样间隔为1s。使用国产接收机和天线，静态采集GPS/BDS/GLONASS三系统数据。图1为试验数据采集环境，图2、图3分别为各卫星系统的可用卫星数和对应PDOP值统计。

图1 试验数据采集环境，基线长65.9 km

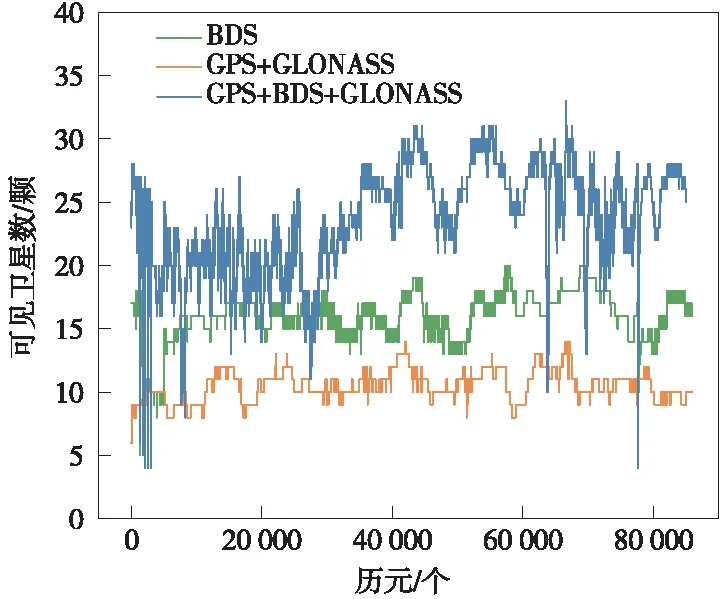
图2 各系统可用卫星数统计

图3 各系统观测PDOP值统计

由图2、图3可知，GPS/GLONASS双系统组合可用卫星数最多为14颗，平均为11颗；BDS可用卫星数最多为20颗，平均为16颗；BDS/GPS/GLONASS三系统组合可用卫星数最多为32颗，平均可用卫星数达到24颗，对应PDOP均值为1.11，相比GPS/GLONASS双系统减小了49.32%。由此可知，BDS-3的建成和使用极大增加了导航卫星系统的可用卫星数，国内BDS-3的可观测卫星数已显著超过GPS/GLONASS双系统，有效改善了卫星空间几何构型。经分析，图中可用卫星数与PDOP值的突变由部分数据异常引起。

会上，上海市燃气管理处副处长莫非致辞，指出，上海市分布式供能项目经过市政府多轮扶持政策取得了长足进步，积累了宝贵的建设和运行经验，初步形成全市产业市场化发展态势，希望通过大家共同努力，推动以分布式供能为基础的区域性能源向能源微网和能源互联网方向发展，实现节能减排、低碳环保可持续发展。

3.2 0.5 h不同系统及定权方法基线解算试验

将24 h试验数据分成48个时段，每个时段0.5 h，对比分析每个时段GPS、GPS/GLONASS、BDS、BDS/GPS/GLONASS组合的基线解算结果。同时，对上述各组合分别采用等权法、高度角定权法、信噪比定权法3种定权方法展开基线解算。不同解算策略下基线解算所得坐标序列如图4～图7所示。

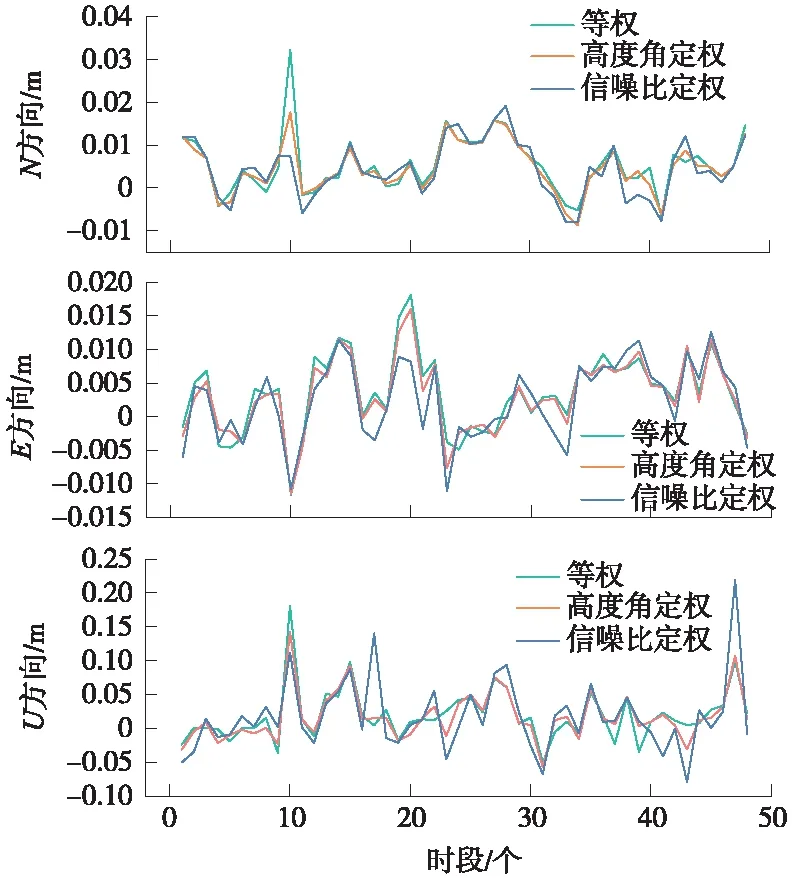
图4 GPS单系统0.5 h观测基线解序列

图5 GPS/GLONASS双系统0.5 h观测基线解序列

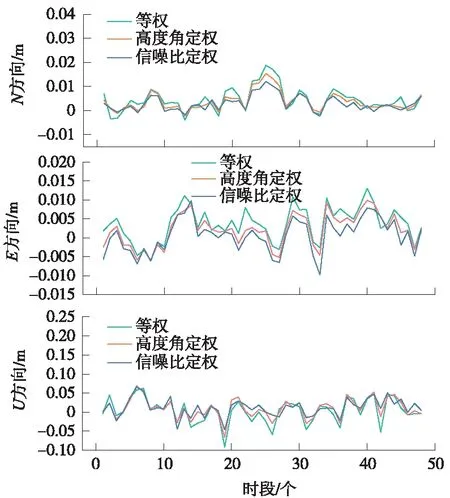
图6 BDS单系统0.5 h观测基线解序列

图7 BDS/GPS/GLONASS三系统0.5 h观测基线解序列

由图4～图7可知，等权法、高度角定权法、信噪比定权法针对不同卫星系统或组合所得到的基线向量N、E、U方向变化基本一致，等权法基线解算结果波动略大于其他两种方法。BDS观测基线解算结果N、E、U方向波动显著小于GPS观测解算结果，且在加入BDS后，BDS/GPS/GLONASS三系统融合的基线解算稳定性显著提高。由此可知，北斗卫星数量上的优势带来了定位性能上的优势。不同解算策略的坐标序列内符合精度统计结果如表1所示。

表1 0.5 h观测不同定权方法基线解算精度统计 m

由表1可知，不同定权方法对水平方向定位精度影响较小，RMS差异在毫米级或亚毫米级，对垂向定位精度影响较显著，RMS差异可达到厘米级。GPS与GPS/GLONASS组合定位时，高度角定权方法性能最优；BDS与BDS/GPS/GLONASS组合定位时，高度角定权和信噪比定权定位精度相当。

高度角定权时，BDS单系统N、E、U方向精度和基线精度比GPS单系统分别高32.76%、21.82%、27.95%和28.07%，比GPS/GLONASS双系统分别高18.75%、12.24%、5.73%和6.27%；信噪比定权时，BDS单系统N、E、U方向精度和基线精度比GPS单系统高51.52%、24.14%、56.06%和55.51%，比GPS/GLONASS双系统高41.82%、20.00%、28.17%和28.31%。由此可知，BDS定位精度优于GPS和GPS/GLONASS组合。

加入BDS系统后，不同定权方法下定位精度均有明显提高。对比BDS/GPS/GLONASS和GPS/GLONASS基线解算结果，采用等权法定权时，三系统观测N、E、U方向精度和基线精度分别提高24.49%、25.00%、31.29%和31.01%；采用高度角定权时，三系统观测N、E、U方向精度和基线精度分别提高29.17%、22.45%、40.86%和39.72%；采用信噪比定权时，三系统观测N、E、U方向精度和基线精度分别提高36.36%、27.27%、47.68%和46.69%。BDS的融入有效提高了GPS/GLONASS基线解算精度，在U方向的效果最为明显。

多系统观测使得可用卫星数增多，不同定权方法的定位精度差异减小。0.5 h观测BDS单系统、GPS单系统、GPS/GLONASS双系统、BDS/GPS/GLONASS三系统对应不同定权方法基线解RMS的极差分别为0.009 2,0.016 1，0.004 5，0.002 5 m。

3.3 不同观测时长基线解算试验

设置观测时长为0.5，1，2，3 h，分别采用等权法、高度角定权法、信噪比定权法给观测值定权，得到不同系统组合下基线解算结果。各观测策略定位结果水平方向和垂直方向精度(中误差)如表2所示。

由表2分析可知，BDS精度整体上优于GPS，BDS/GPS/GLONASS三系统组合在任何策略中均取得最优精度，当观测时间较短时，其精度优势更为显著。以0.5 h高度角定权解算为例，BDS解算水平、垂向精度较GPS分别高0.002 3,0.010 2 m，BDS/GPS/GLONASS三系统解算水平、垂向精度较GPS/GLONASS双系统分别提高了26.09%、40.86%。

表2 不同观测时长基线解算精度(中误差)统计 m

在各观测时长和系统组合条件下，采用不同定权方法解算得到的基线向量水平方向精度基本相当，RMS差值在毫米级或亚毫米级，垂向精度差异较显著，RMS差值可达到厘米级。3种定权方法中，等权法整体精度最低，高度角定权法稳定性最高，且在GPS系统和GPS/GLONASS双系统组合中优势明显。以GPS/GLONASS双系统垂向精度为例，观测0.5,1,2,3 h在高度角定权策略下基线解算结果比信噪比定权分别高0.004 4,0.004 4,0.003 0,0.003 7 m。融入BDS后，三系统组合0.5 h观测时长的基线解算精度与单GPS 2 h的解算精度相当。

随着观测时间的延长，各定权方法、各系统组合下基线解的水平精度和垂向精度均有明显提高。以BDS/GPS/GLONASS三系统组合为例，对比0.5 h和3 h观测基线解精度的变化情况，水平、垂向精度在等权策略下分别提高24.53%、32.46%，高度角定权策略下分别提高25.49%、41.82%，信噪比定权策略下分别提高26.42%、49.11%。随着观测时间延长，不同定权方法间定位精度的差异呈减弱趋势，在GPS单系统、BDS单系统和GPS/BDS双系统组合中尤为明显。融入北斗系统后，三系统融合解算时，不同观测时长条件下，不同定权方法的中长基线解算精度的差异减小，水平和垂向差异分别为1 mm和5 mm。

4 结论

在分析BDS/GPS/GLONASS多系统基线解算函数模型及观测值先验定权方法的基础上，利用融合北斗三代的全星座铁路框架网中长基线观测数据，通过试验对比分析等权法、高度角定权法、信噪比定权法，在不同卫星系统组合和观测时长策略下的定位精度，得到以下结论。

(1)0.5h观测时长高度角定权解算策略下，BDS系统相比于GPS系统基线精度高28.07%，融入BDS后，三系统基线解算精度提高了39.72%。新一代BDS中长基线解算精度优于GPS，融入BDS系统后，三系统组合的基线解算精度显著提升。

(2)等权法、高度角定权法、信噪比定权法3种定权方式中，高度角定权法总体稳定性优于信噪比定权与等权方法。融入BDS后，三系统组合0.5 h观测时长的基线解算精度与单GPS 2 h的解算精度相当，两者水平精度分别为0.004 9 m和0.005 1 m，垂向精度分别为0.016 5 m和0.021 0 m。BDS对实现中长基线快速解算作用显著。

(3)0.5 h GPS单系统观测下不同定权方法基线中误差极差为0.016 1 m，而BDS/GPS/GLONASS三系统观测不同定权方法基线中误差极差减小到0.002 5 m。随着观测时长的增加，不同定权方法间定位效果差异表现出弱化趋势。融入北斗系统后，三系统融合解算时，不同观测时长条件下不同定权方法的中长基线解算精度的差异减小，水平和垂向差异分别为1 mm和5 mm。

可见，相较于GPS系统，融入新一代BDS系统后多星座GNSS对铁路框架网控制测量的定位精度和作业效率的提升效果显著，BDS可为后续铁路框架网的作业流程优化提供基础条件。