基于深度信念网络的昌都林芝区域滑坡易发性评价

净文常,李孝攀,杨家鸣

(1.中铁第一勘察设计院集团有限公司,西安 710043； 2.中南大学土木工程学院,长沙 410075)

引言

昌都林芝区域位于青藏高原东南部，地貌形态受青藏高原地貌隆升的影响，总体地势西高东低。地势急剧隆升抬起，河流快速强烈下切，为典型的“V”形高山峡谷地貌，地貌形态以丘状高原及构造侵蚀形成的深切峡谷地貌为其总体特征。该区域自东向西可划分为横断山高山峡谷区及藏南高山峡谷区两个地貌单元，伯舒拉岭作为两个地貌单元的分界，也作为为昌都市和林芝市的分界，更是三江(金沙江、澜沧江、怒江)流域和雅鲁藏布流域的分水岭。昌都林芝区域滑坡灾害分布广泛且尤为突出，在该区域内开展工程建设有较大的工程风险。因此，查明该区域的滑坡分布规律及其易发属性，对拟建工程的建、管、养工作具有重要作用。

对滑坡进行风险评价和管理作为国际上积极倡导和推广的有效减灾途径。总体而言，其流程一般包括滑坡区域确定、易发性分析、危害分析和风险计算4个逐步递进的步骤。其中，滑坡易发性分析是风险评价和管理的基础和核心环节，即通过获取滑坡分布数据，确定其分布规律，分析滑坡灾害因子与滑坡发生的关系，从而定性或定量分析出现有或潜在的滑坡空间分布和发生概率。滑坡易发性评价有利于风险分析及预防管理，对减少滑坡灾害损失至关重要。

滑坡易发性评价是依托区域空间信息及地理资料，对滑坡特性(发生概率等)的定性或定量评估，最早起源于1970年[1]。现阶段，滑坡易发性方面研究一般采用启发式分析及概率性统计两类方法。其中，启发式分析主要指以专家主观经验为基础，依托研究区域的历史数据，分析给出区域的滑坡灾害特征，层次分析法[2]等是其中的典型方法；而概率性统计则是利用概率学模型，基于区域的地理特征及灾点分布概况，预测区域各部分的滑坡发生概率，Logistic回归[3]等表现出色。概率性统计方法由于评价准则客观科学，且能较好处理线性及非线性问题，其结果精度和可靠度往往优于启发式分析方法。然而，对于高维空间的复杂问题，概率性统计方法不可避免地存在欠拟合，预测准确度不高。目前，由于计算机性能的日益强大，支持向量机[4]、BP神经网络[5]等机器学习模型开始用于滑坡易发性分析，其依托有监督的反馈训练机制，能使构建的模型逐步契合实际情形，以保证模型精度高于传统的概率性统计方法。其中，深度信念网络(DBN)[6]等深度学习模型，以其更深层次、更为复杂的架构深入分析滑坡诱发规律，在滑坡易发性评估中通常取得精度更高的结果。

对此，本研究将基于昌都林芝区域的地理属性及空间信息，建立DBN网络架构，结合区域内的滑坡灾害分布情况，获取该区域内各单元的滑坡易发性，评判昌都林芝区域的滑坡风险，为该区域的工程建设提供一定的理论指导，为滑坡灾害风险规避及土地综合利用提供一定的理论支持。

1 研究区域和数据集

1.1 昌都林芝区域概况

昌都林芝区域位于西藏东南区域，其间主要的交通道路有G318、G317和G214，昌都市卡若区、察雅县、八宿县、洛隆县，林芝市波密县和巴宜区两市六区县人口占据了昌都市和林芝市总人口的50%，正在大规模开展基础设施建设，滑坡灾害对改区域的影响更大，因此选择此两市六区县作为研究区域，研究区域如图1所示。

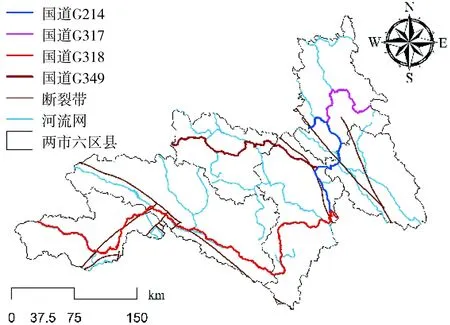
图1 昌都林芝区域(两市六区县)

从地形地貌方面分析，昌都林芝区域受青藏高原地貌隆升作用，总体地势呈现西高东低，为典型“V”形地貌，并表现出丘状高原及深切峡谷特征；在地质方面，昌都林芝区域构造极其发育，褶皱断裂密集分布，并以深大活动断裂为主控，其中共有3个一级构造，分别为冈底斯—念青唐古拉地块、班公湖—怒江缝合带、羌塘地块，以及5个二级构造，如喜马拉雅地块等。此外，昌都至林芝区域地层岩性十分复杂，地层时代从震旦系至新生界均有分布，并伴随多种复杂不良地质，其中以高位远程滑坡较为典型；在水文方面，昌都至林芝区域的地表水系主要涉及澜沧江、怒江、雅鲁藏布江三大河流，而地下水系则以第四系孔隙潜水、基岩裂隙水、构造裂隙水和岩溶水为主；在气候上，昌都林芝区域以伯舒拉岭为界线，东部为高原亚温带亚湿润气候区(昌都地区)，西部为高原温带湿润半湿润季风气候区(林芝地区)。

1.2 历史滑坡信息

考虑到建立机器学习模型往往需要区域内的滑坡分布数据，本研究选定昌都林芝区域两市六区县的面状领域作为范围界定。基于此利用GIS平台实现纸质图件数字化，并从中国科学院资源环境科学与数据中心、国家地球系统科学数据中心及MAPGIS开源数据库等获取有关数据进行补充，整合形成了该范围内的滑坡信息数据集，共有324个滑坡点，具体分布概况如图2所示。

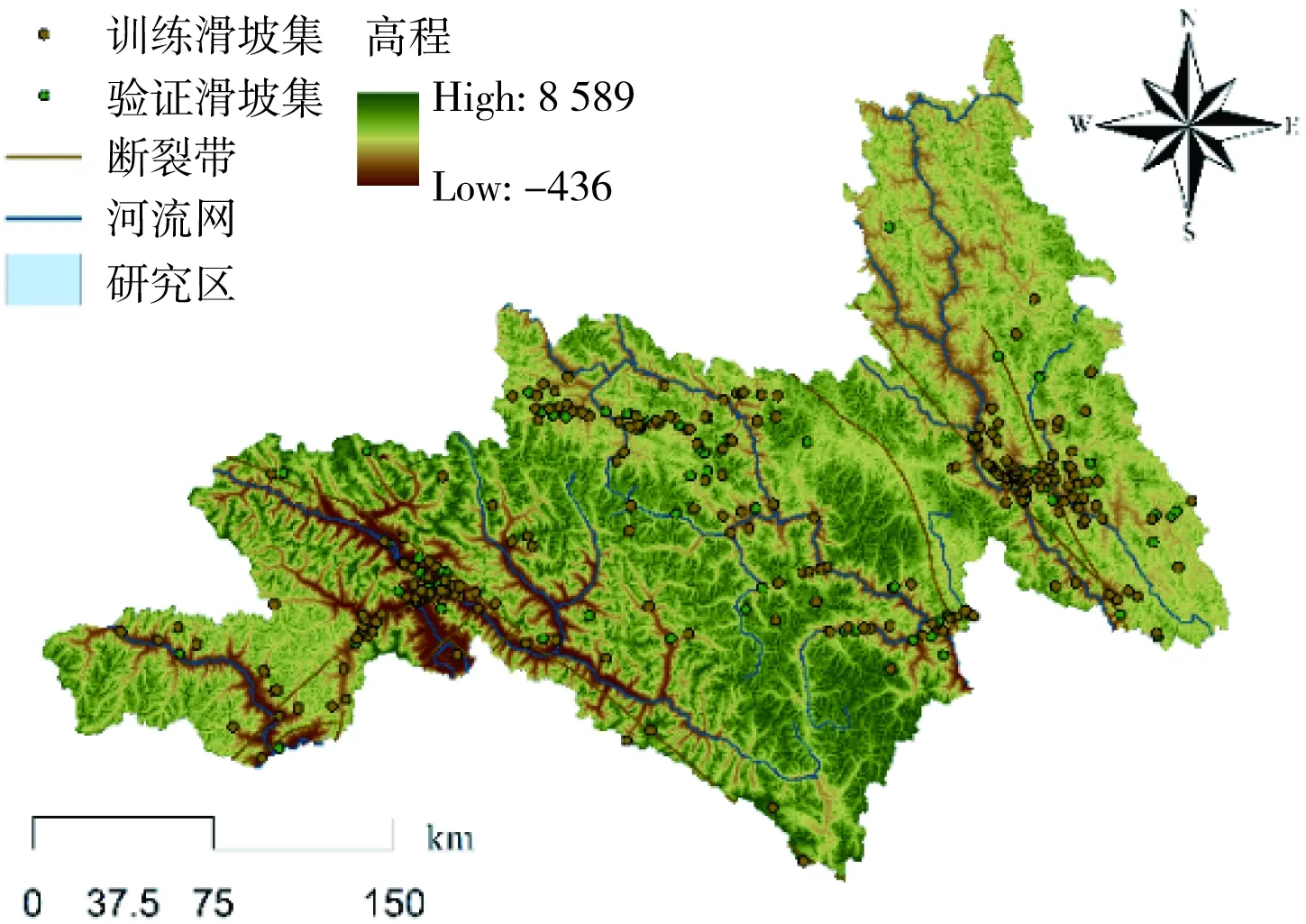
图2 昌都林芝区域的滑坡分布概况

1.3 致灾因子数据

通常情况下，滑坡灾害的发生是多重因素相互作用的综合产物，而这些与滑坡灾害具有显著联系的因素便是致灾因子。有研究[6]指出，致灾因子选取的合理性往往对滑坡易发性的评价结果至关重要。对此，本研究依托前人的研究成果[7]，并结合昌都林芝区域地势极高及活动断裂特征明显等自然特性，从地形地貌、地质特征、水文环境、人类活动4个方面分析滑坡发生机制，选取了高程[8](图3)、坡度[9](图4)、坡向[10](图5)、地形起伏度[11](图6)、岩性[12](图7)、距断裂带距离[13](图8)、植被覆盖度[14](图9)、降雨量[15](图10)、距水系距离[16](图11)、距道路距离[17](图12)10个致灾因子，其具体表述如表1所示。

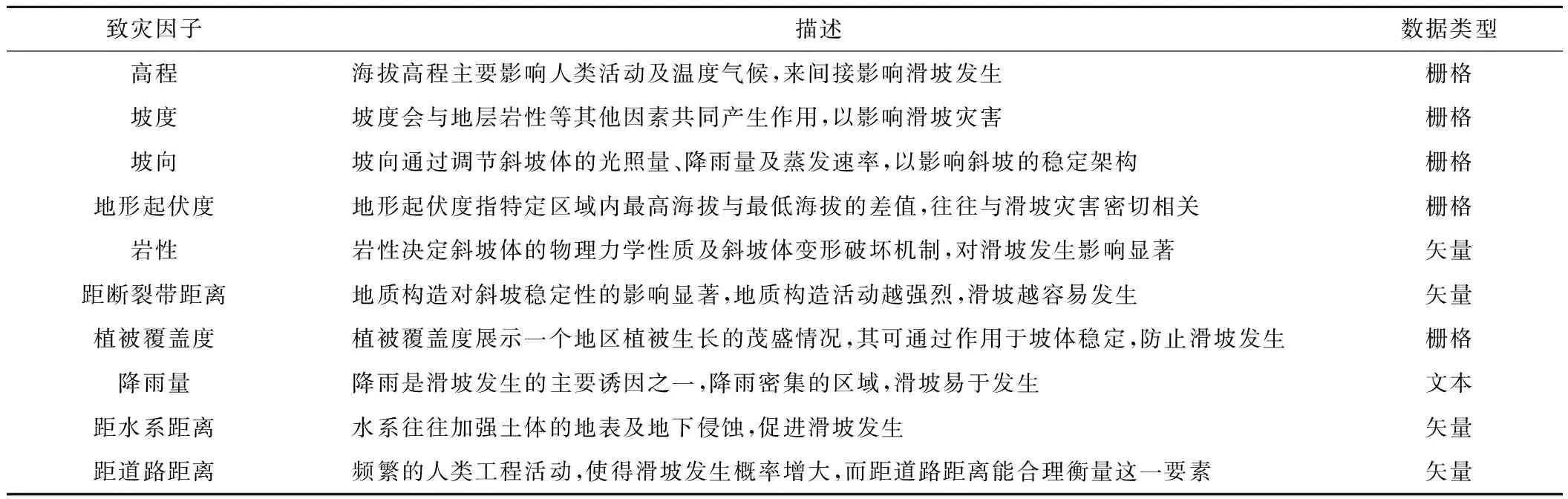
表1 昌都林芝区域的滑坡致灾因子数据说明

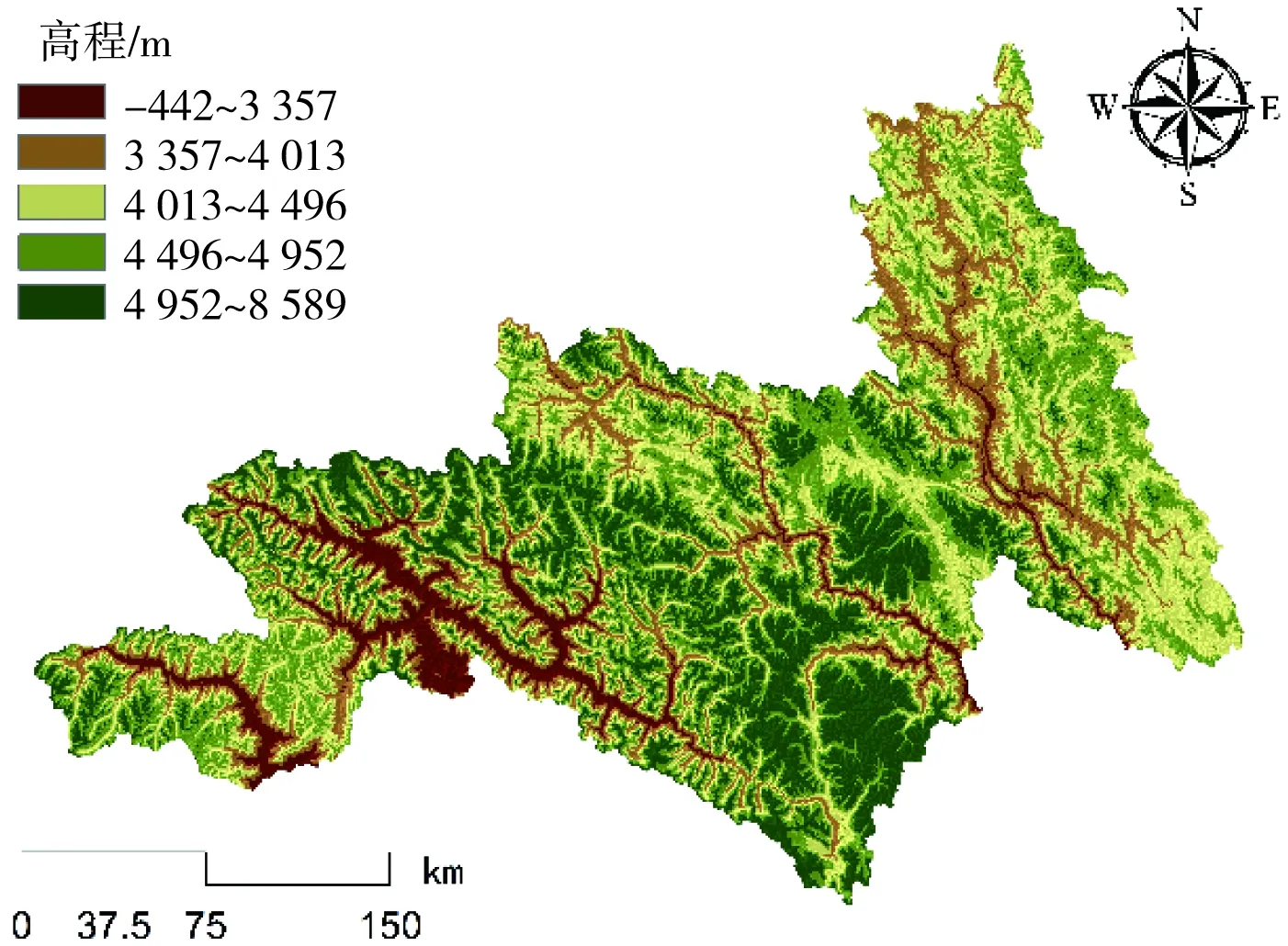
图3 昌都林芝区域高程分布

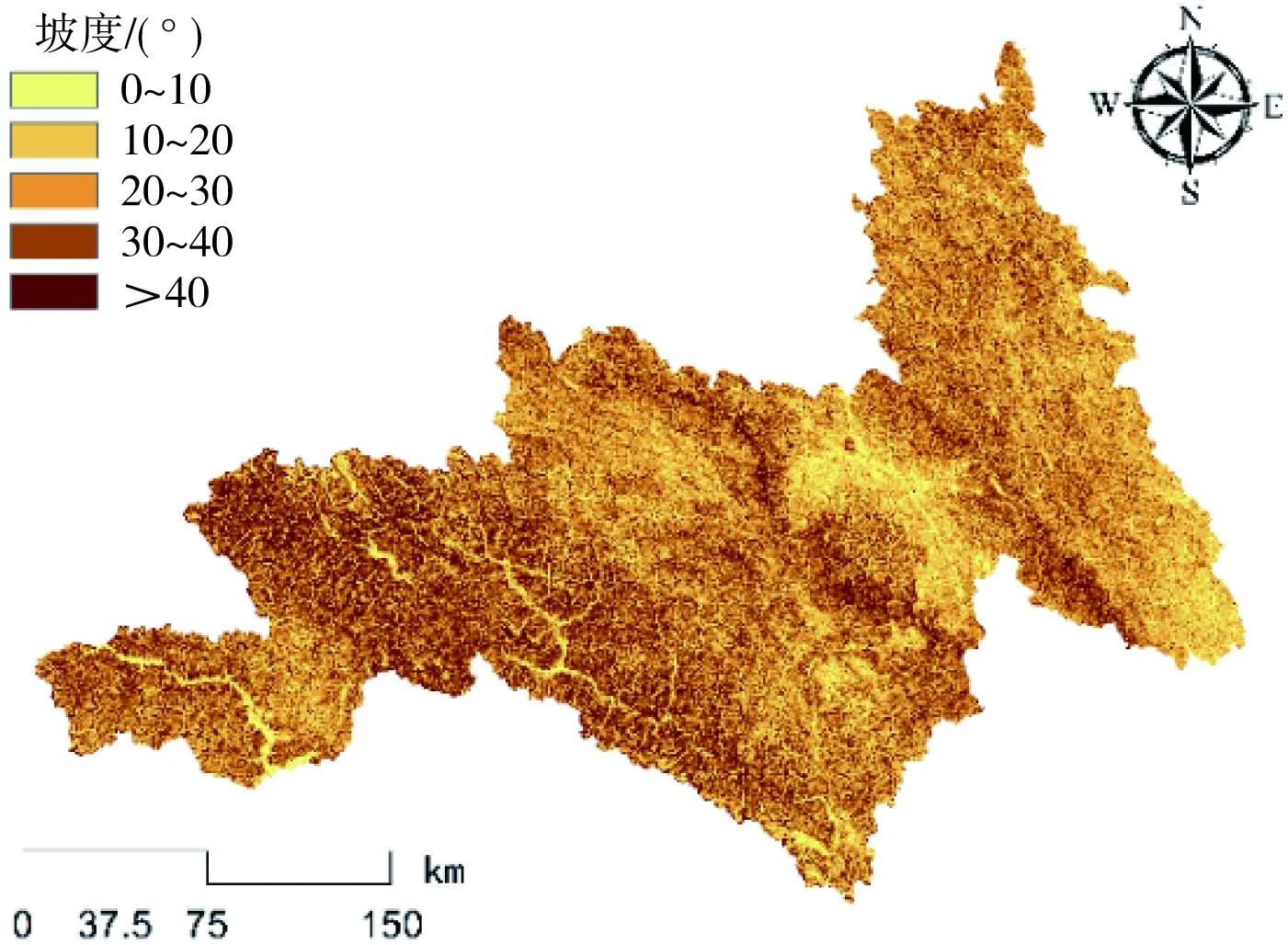
图4 昌都林芝区域坡度分布

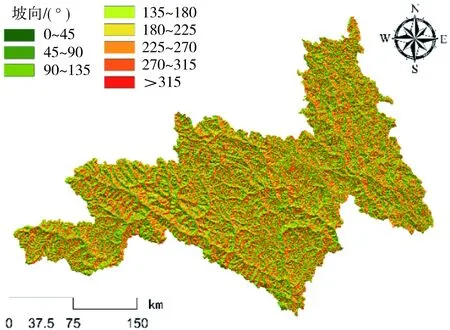
图5 昌都林芝区域坡向分布

图7 昌都林芝区域岩性分布

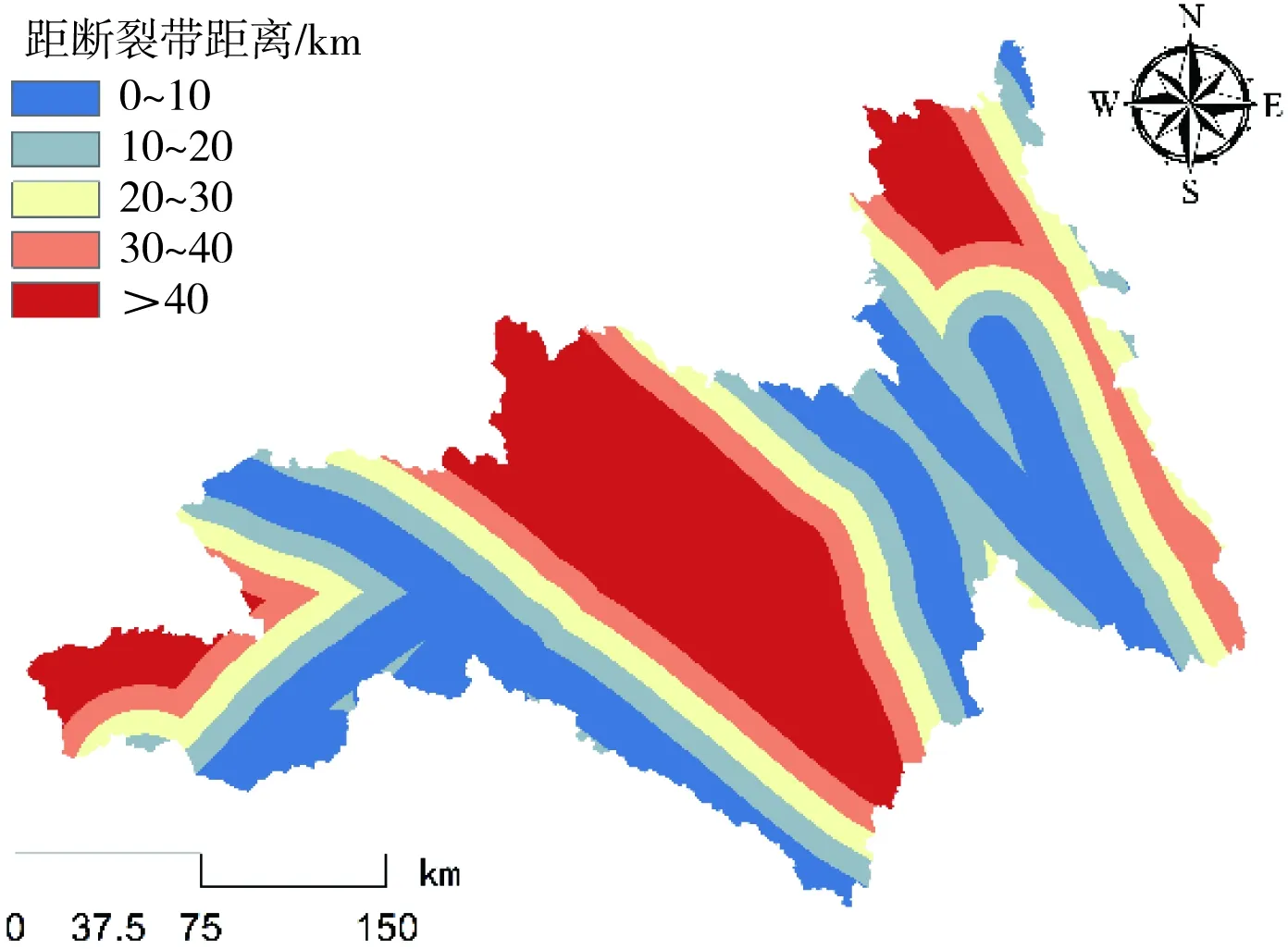
图8 昌都林芝区域距离断裂带距离分布

图9 昌都林芝区域植被覆盖度分布

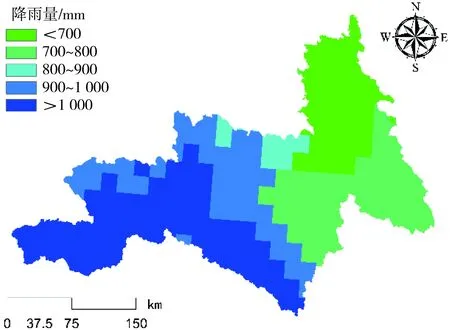
图10 昌都林芝区域降雨量分布

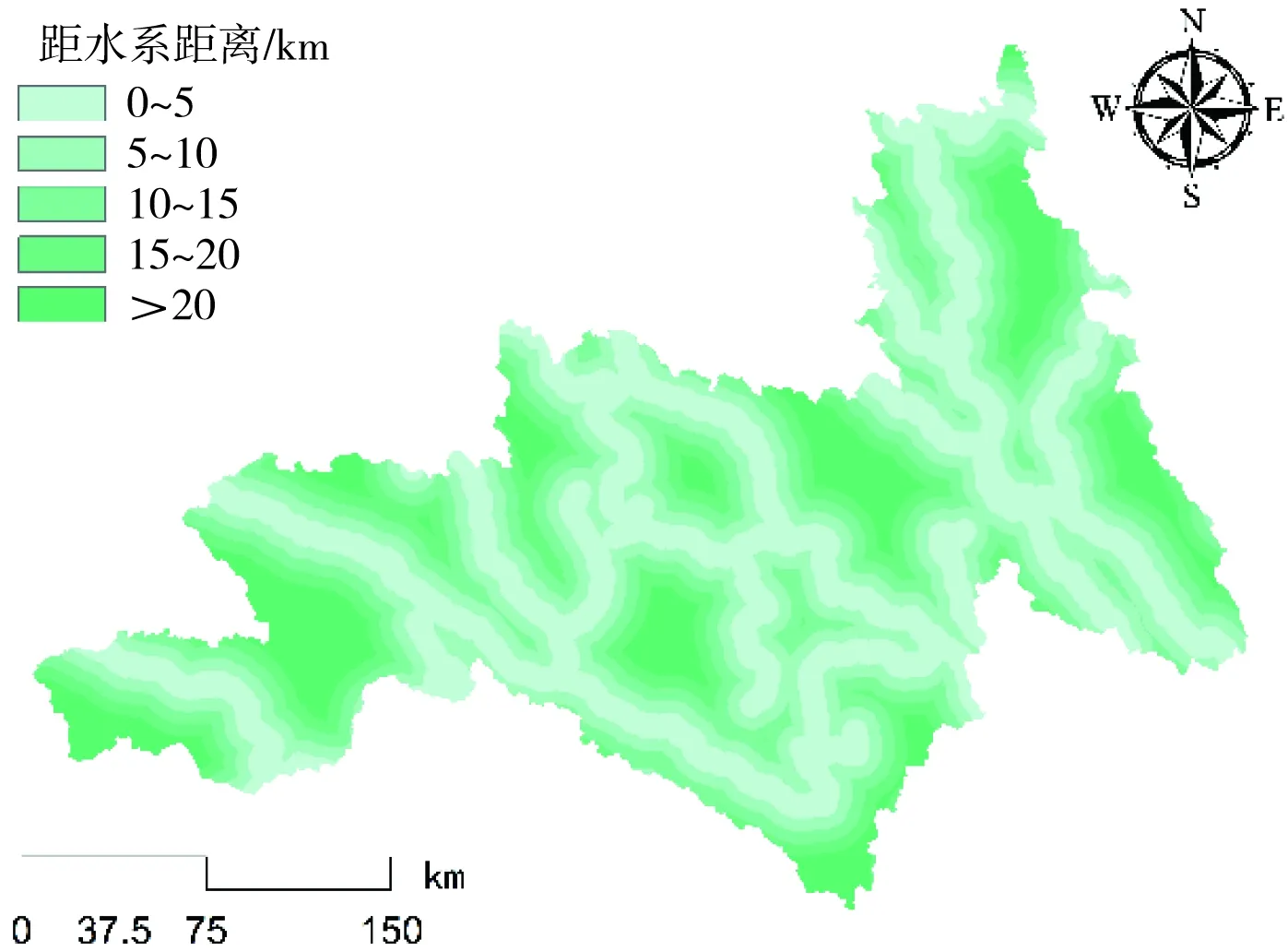
图11 昌都林芝区域距离水系距离分布

图12 昌都林芝区域距离道路距离分布

2 易发性区划模型

为有效评估昌都林芝区域的滑坡易发性，需基于区域的水文分布情况及地理特征，对区域进行单元划分，而后利用训练好的模型进行逐一分析，以进行各区划单元的易发属性提取。对此，本研究具体可以分成3步。一是数据整理，主要为准备模型训练、模型验证及模型预测数据集，为相应的模型建立及区划分析提供数据支持；二是滑坡易发性评价，主要是基于昌都林芝区域内的滑坡历史分布，利用性能较好的DBN深入分析区域内的滑坡诱发机制，而后将区域单元输入模型，提取昌都林芝区域的滑坡概率特征。同时，本研究还依托SVM、BP、Logistic回归获取区域的滑坡发生概率，为后续模型性能比对予以支撑；三是模型性能评估，具体为利用区划数据统计结果及ROC曲线，验证基于DBN评估结果的科学性及合理性。

2.1 数据整理

在建立滑坡易发性评价模型前，需要对灾点数据集、区域致灾因子数据集进行整理，并将其分成模型训练、模型验证、模型预测数据集，以更好地支持后续的滑坡易发性区划与评估。

一般而言，依托机器学习模型进行滑坡易发性评估时，各分类样本的比例接近1∶1，模型性能达到最优。对此，本研究主要采集了线路区域内324个滑坡点，相应地需要获取324个非滑坡点。于此，本研究利用GIS平台的生成随机点工具，在区域内任意生成了324个样本点作为非滑坡点。而后，本研究将324个滑坡点及非滑坡点整合，提取了共648个点的高程、坡度、坡向等10个致灾因子数据，形成了灾点数据集。为了保证模型训练性能及避免出现过拟合，本研究将灾点数据集按7∶3分成两部分，分别作为模型训练、模型验证数据集。

考虑到昌都林芝区域内各部分地理特征差异明显，本研究将基于区域属性进行区域单元划分，予以昌都林芝区域的滑坡易发性提取有力支撑。目前，区域单元主要有栅格单元、斜坡单元、地貌单元、行政单元和唯一条件单元五种[18]。其中，斜坡单元充分考虑了地形分割的边坡情况，与实际地貌的切合程度较高，对区域属性的准确获取十分有利[19]。对此，本研究对区域进行斜坡单元划分，具体为设定河流阈值为1 000，将区域划分成224 102个斜坡单元。随后，本研究提取了这224 102个斜坡单元的高程、坡度、坡向等致灾因子信息，整合成模型预测数据集。

2.2 滑坡易发性评价

考虑到DBN的性能优越，本研究主要依托DBN分析滑坡易发性，并引入SVM、BP、Logistic回归作为对比模型，以验证DBN的性能。其中，DBN、SVM、BP及Logistic模型的具体阐述如下。

2.2.1 DBN深度信念网络

深度信念网络是一种深度学习的生成模型，由Geoffrey Hinton在2006年提出。它是由多个受限玻尔兹曼机(Restricted Boltzmann machine，RBM)堆叠而成，并在最后一层建立BP全连接层进行预测及回归，实现了无监督和有监督的交叉整合。其中，RBM作为模型先导部分，可对输入数据进行无监督预训练，依托贪婪算法深入剖析数据间隐藏特征，并将其输出作为后续BP层的输入；而BP层则可进行维度裁剪，将高维特征降低到预期的维度空间内，同时利用Sigmoid激活函数进行数据收缩，保证输出数据的值域可控。因此，DBN可有效处理数据分类问题，有利于精准实现滑坡易发性的提取。

为保证模型的精度，本研究进行了多次调参，最终设置了隐藏单元数为100、50、20的三层RBM结构，用于数据预分析，并将BP层的输入节点数设为10，代表10个滑坡影响因子，输出节点数设为1，代表区域斜坡单元的滑坡发生概率。其中，BP层的优化器为Adam，损失函数为Mean squared error(MSE)，迭代次数为3 000次，学习率为0.001，训练批次为100。

2.2.2 比对模型

(1)SVM

SVM是一种有监督的机器学习算法，其基础源于Corinna Cortes和Vapnik于1995年提出的软边距非线性SVM理论。SVM的本质思想是结构风险最小原则，基本原理是数据的维度映射，具体是通过将低维度空间内混杂的、不可划分的数据投影到高维度空间内，并在相应的高维度空间内寻找最优分类超平面，以实现数据的正确分类。

需要注意的是，SVM中的数据投影核函数对模型精度的影响十分显著。在本研究中，将核函数设定为Radial basis function (RBF)，以更好展示致灾因子与滑坡灾害间的非线性关系，并将惩罚系数设定为0.05，用于有效防止模型过拟合。

(2)BP

BP神经网络结合了误差反向传播算法的人工网络模型，由Rumelhart和McClelland于1986年提出。该模型的核心原理是模拟人类大脑的神经元结构，以建立推理模型，其本质仍属于非线性动力学系统，具有较强的非线性函数逼近能力，并表现出自适应、高容错、学习能力强的特性。典型的BP网络结构有输入、隐藏、输出三层，其通过正向传递和逆向反馈机制进行迭代训练，以提高模型精度。

在依托BP评价滑坡易发性时，本研究主要基于多层感知器(MLP)进行模型构建。其中，本研究将输入层设为10，对应10个致灾因子，隐藏层设为10，输出层设为1，并将输出层的激活函数设为“Sigmoid”，用于输出概率。

(3)Logistic回归

Logistic回归[20]是一种多元统计方法，其本质是依托多个自变量和1个因变量间的数据特征，建立多对一的回归关系。该模型可以根据建立的函数关系和输入的自变量求解任一研究领域任一事件的发生概率，并具有变量约束不强的优点。其具体的计算公式如下

(1)

式中，β0为常数项；βi为xi的逻辑回归系数；ρ为概率。

一般而言，Logistic回归并不需要过多的参数设置。于此，本研究在利用Logistic回归模型评价滑坡易发性时，仅将惩罚系数设定为0.1，用于防止模型训练的过拟合情形。

2.3 模型性能评估

在实现滑坡易发性评价后，本研究将从2个方面去评估模型性能。一是对DBN等4个模型的区划结果进行统计，获取各易发性等级内的滑坡数量、区域面积及滑坡点密度，分析比对模型的预测情况；二是引入ROC曲线以辅助评估。ROC曲线，是基于真假阳性率绘制的一种坐标图式分析工具，用以反映变量的特异、敏感性及模型精度。通常情况下，ROC的曲线下方面积值(AUC)处于[0，1]之间，且AUC越大，模型精度越高。一般而言，模型的AUC值达到0.9，可认为建立模型的性能十分出色。于此，本研究将利用AUC值评价模型的预测性能。

3 易发性区划结果

3.1 区域滑坡易发性区划

依托上述流程可知，本研究首先利用DBN、SVM、BP、Logistic回归获取了区域内224 102个斜坡单元的滑坡概率，而后需要对其进行滑坡易发性等级划分。目前，滑坡易发性区划的方法以自然间断点法为主，其基本原理是对分类间隔进行深入识别，以保证同一类别间的差异最小，不同类别间的差异最大。自然间断点法可以有效提取数据分隔节点，使得数据的分类效果显著。然而，自然间断点法不可避免地存在随机性，如滑坡发生概率相同的区域在不同条件下(不同区域、不同模型)可能会被归为不同的滑坡易发性等级，这导致了模型的相互比较缺乏依据。对此，本研究引入了戴福初等[21]的研究成果，将各斜坡单元分成极低(<0.1)、低(0.1～0.3)、中(0.3～0.5)、高(0.5～0.75)、极高(>0.75)5个级别，制定了区域滑坡易发性区划图(图13～图16)。这种方法的好处在于给出了十分明确的数据划分节点，保证了区域滑坡易发性等级评估的唯一性，同时为不同模型区划性能间的比较提供了有力支撑。最后，为了展示模型区划结果的差异性，本研究还统计了图层内各级别的滑坡数量、区域面积及滑坡密度(表2)。

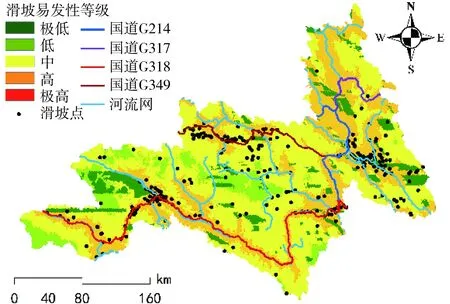
图14 基于Logistic回归的区域易发性评价

图15 基于BP的区域易发性评价

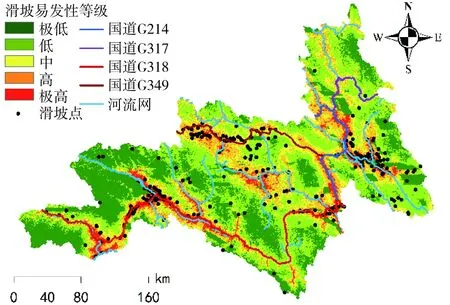
图16 基于DBN的区域易发性评价

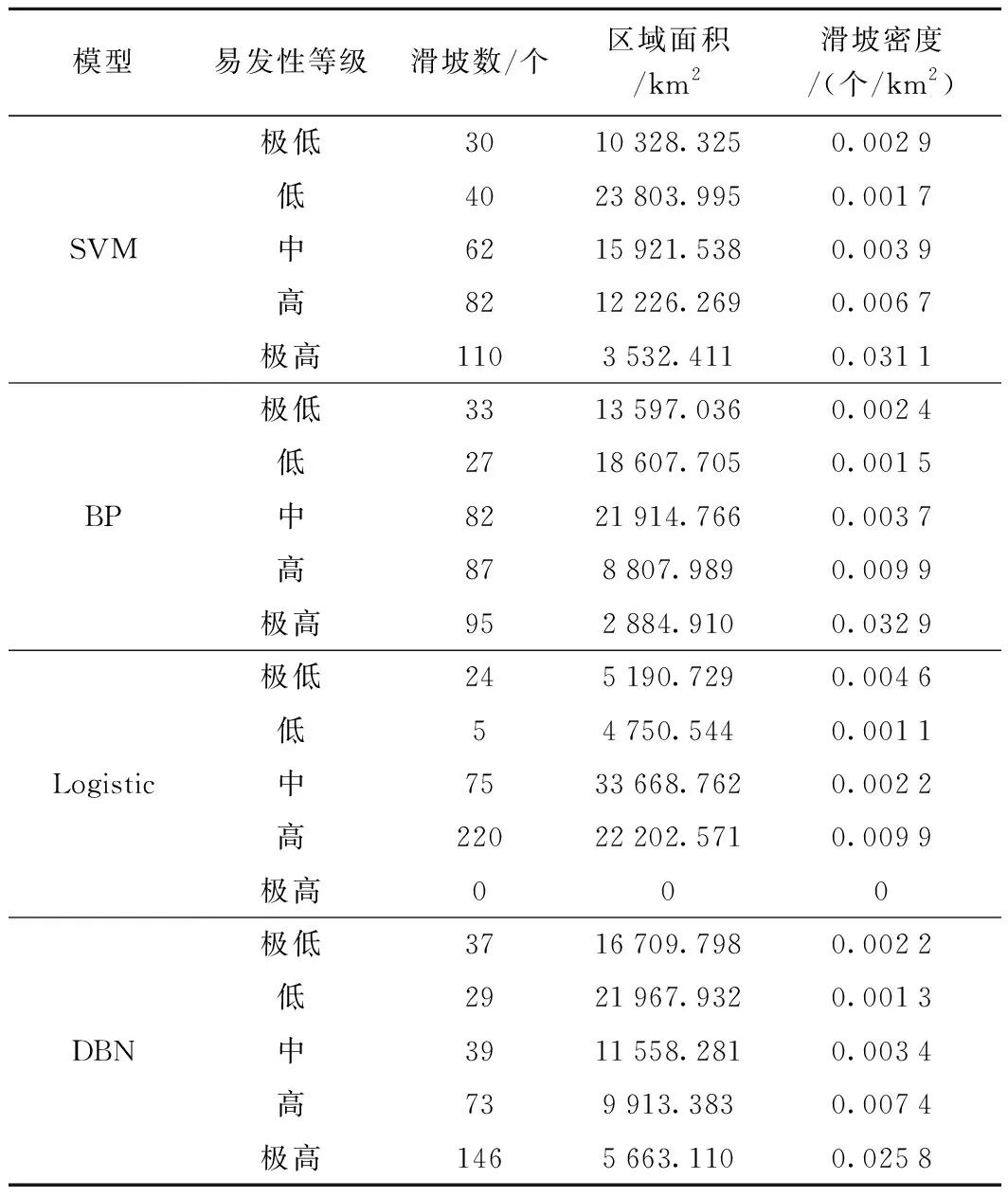
表2 基于SVM、BP、Logistic及DBN的区划结果统计

根据图表数据显示，DBN、SVM、BP、Logistic回归的区划结果存在一定的相似性，这是因为模型的区划结果均表明，滑坡高易发区域呈带状贯穿整个线路所经地区，其形状高度契合区域内的河流走向及国道分布，而滑坡低易发区域则呈块状分布于高易发区域附近；其次，Logistic回归的区划结果并未包含极高滑坡易发性区域，这说明Logistic回归的区划结果不尽合理，而由DBN、SVM、BP的区划结果可知，滑坡点密度与各滑坡易发性等级基本呈正向关系，展示了区划结果的科学性；最后，从图17中的滑坡历史灾点在各易发性等级中的占比分布数据看，在基于DBN的区划结果中，位于极低、低区域的滑坡总比例为20.370%，优于SVM的21.605%，略差于BP的18.519%，而DBN的极高、高区域滑坡占比达67.593%，远大于SVM的59.259%和BP的56.173%，这展示了DBN的区划结果更契合于实际滑坡分布。此外，在滑坡密集分布地带，DBN的区划结果均为极高易发性区域，这揭示了DBN的数据挖掘能力更好。

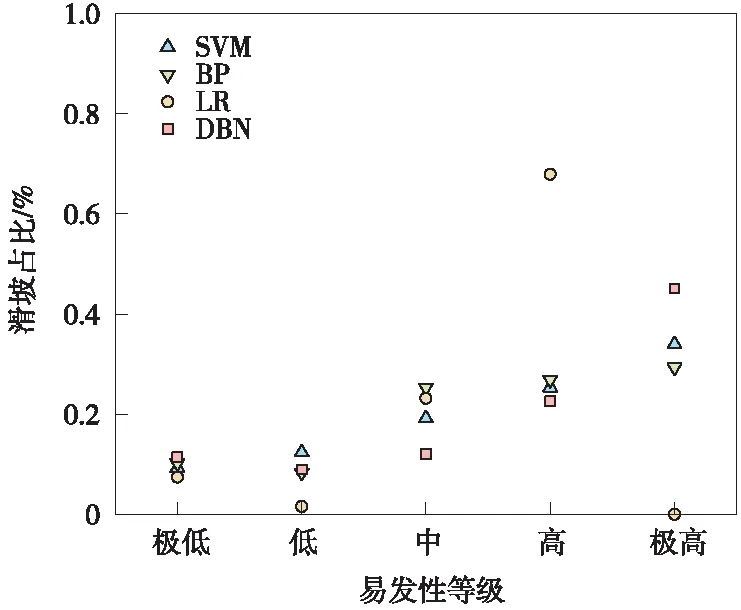
图17 各易发性等级中的滑坡占比

3.2 ROC曲线精度评估

为了评估SVM、BP、Logistic回归、DBN的预测性能，本研究绘制了这4个模型的ROC曲线图，并获取了其曲线下面积AUC值(图18)。

图18 SVM、BP、Logistic回归及DBN的ROC曲线

由图18可知，4个模型的AUC值均在0.85以上，表明它们的预测性能均较好。而在这4个模型中，以DBN的表现最为出色，其AUC值为0.90，优于SVN的0.88、BP的0.88和Logistic的0.87。

3.3 昌都林芝区域滑坡易发性区划结果分析

依托DBN的区域滑坡易发性评价结果，昌都林芝区域滑坡发生概率较大，其极高、高滑坡易发性区域的占比达67.593%。其中，极高滑坡易发性区域高度契合于河流及道路走向，在河流、道路网密集处，往往更倾向于发生滑坡，如伯舒拉岭附近的三江汇流地带及214国道、317国道的交界处等。因此，在河流及道路附近区域建设工程时，需要注意滑坡防治和风险转移，尤其是河流网及道路网密度较高的区域。

4 结论

(1)选定了昌都林芝区域的滑坡灾害致灾因子。以昌都林芝两市六区县为研究对象，从地形地貌、地质特征、水文环境、人类活动四方面确定了昌都林芝区域滑坡致灾因子体系，并利用区域324个滑坡历史灾点及各因子数据集构建了基于DBN的滑坡易发性评价模型。

(2)验证了深度信念网络的精度。针对昌都林芝区域，ROC曲线的精度评估表明DBN的滑坡易发性预测性能较好，优于SVM、BP及Logistic回归。此外，DBN具有较好的可移植性，其仍能有效用于评估相似区域的滑坡易发性。

(3)利用二维领域内表现出色的DBN评价了昌都林芝区域的滑坡易发性。研究结果显示，昌都林芝区域滑坡极高易发性区域分布集中，主要分布于河流和道路两侧，在后续开展工程建设时应适当远离河流和道路。