地铁列车运行诱发的地面振动响应特性分析

李 平,王明昃,赵 晨,裴 鑫,王 威,冯青松

(1.广州地铁设计研究院股份有限公司,广州 510330； 2.华东交通大学铁路环境振动与噪声教育部工程研究中心,南昌 330013)

引言

随着我国经济的高速发展，城市规模也在快速扩大，在多数城市中，一般地面交通系统已经无法完全满足日益加剧的交通需求。此时运量大、效率高的地铁交通系统逐渐成为改善城市交通压力的关键手段。但地铁交通在带来便捷的同时，由自身振动问题所带来的环境危害也日益凸显。地铁列车运行引起的地面振动受列车运行速度、轨道结构、轨面埋深、地质条件、建筑物结构形式等多种因素影响较大[1]。近年来，不少学者针对地铁列车运行引发的振动相关问题进行了大量研究，目前有关地铁列车运行引起的环境振动响应研究主要包括3个方面：对地铁列车运行引起的地面振动研究[2-4]，对地铁沿线附近的高精仪器影响研究[5-7]，对邻近建筑影响研究[8-10]。

针对地铁引发的振动问题，数值模拟分析方法由于其具有精度好、效率高等优点而广被研究人员采用。郑国琛等[11]基于某实际Ⅱ类场地的地铁与道路交通重合段进行振动实测，同时建立了简化有限元模型，分析地铁振动对于周围环境的影响；岳建勇[12]结合上海地区典型软土工程，提出有限元与无限元相结合的数值分析方法，对由地铁引起的周围建筑物振动响应情况进行预测分析，同时结合实测数据对比分析验证了分析方法的可行性；张波等[13]基于青岛地铁3号线，建立了计算模型，并分析了不同深度岩层弹性模量改变对振动响应的影响规律。

在经验公式研究方面，付丽[14]基于HJ 453—2008《环境影响评价技术导则—城市轨道交通》中的振动环境影响预测计算公式，通过大量现场实测，提出了预测计算公式距离修正项中参数a、b值；杨光辉等[15]通过大量现场实测数据，建立了可反映地表振动响应与距离之间关系的模型；蒋通等[16]通过非线性回归和线性回归两种方法，推导出了上海市轨道交通高架线环境振动的衰减经验预测模型；闫维明等[17]基于地铁现场实测数据，分析发现地面振动响应存在振动放大区，并提出了Z振级统计回归方程。

综上所述，关于地铁列车运行引起的地面振动方面的研究成果已相当丰硕，但当前研究多就影响地面振动情况的单个或少数几个因素进行了一定研究，对于地铁列车运行诱发的地面振动影响因素仍需做深入研究。为此，在上述研究基础上充分考虑了不同轨面埋深、隧道周围土层、运行车速、列车车型、减振扣件及建筑物影响。

为进一步分析地铁列车运行引起的地面振动响应特性，利用ANSYS/LS-DYNA分析软件，建立了振动响应分析模型，并实测了广州地铁1号线某区间实际振动数据，通过实测与仿真对比验证了该模型的准确性，研究不同轨面埋深、隧道周围土层、运行车速、列车车型、减振扣件及建筑物对地铁列车运行引起的地面振动响应特性的影响，以期为有关工程提供一定参考。

1 计算模型

1.1 模型建立

利用ANSYS/LS-DYNA计算软件建立振动响应分析模型，模型主体分为地铁车辆-轨道耦合垂向振动模型和隧道-土层有限元模型两部分。研究中，隧道采用圆形盾构隧道结构，列车车型为A型车，车型设计参数的选定参考广州地铁设计研究院及过往经验数据得到，具体参数如表1所示，道床结构为整体道床。在仿真计算时，首先通过地铁车辆-轨道耦合垂向振动模型计算出相应的振动响应，再将其施加于隧道-土层有限元模型上进行地面振动响应分析，有限元计算模型如图1所示。

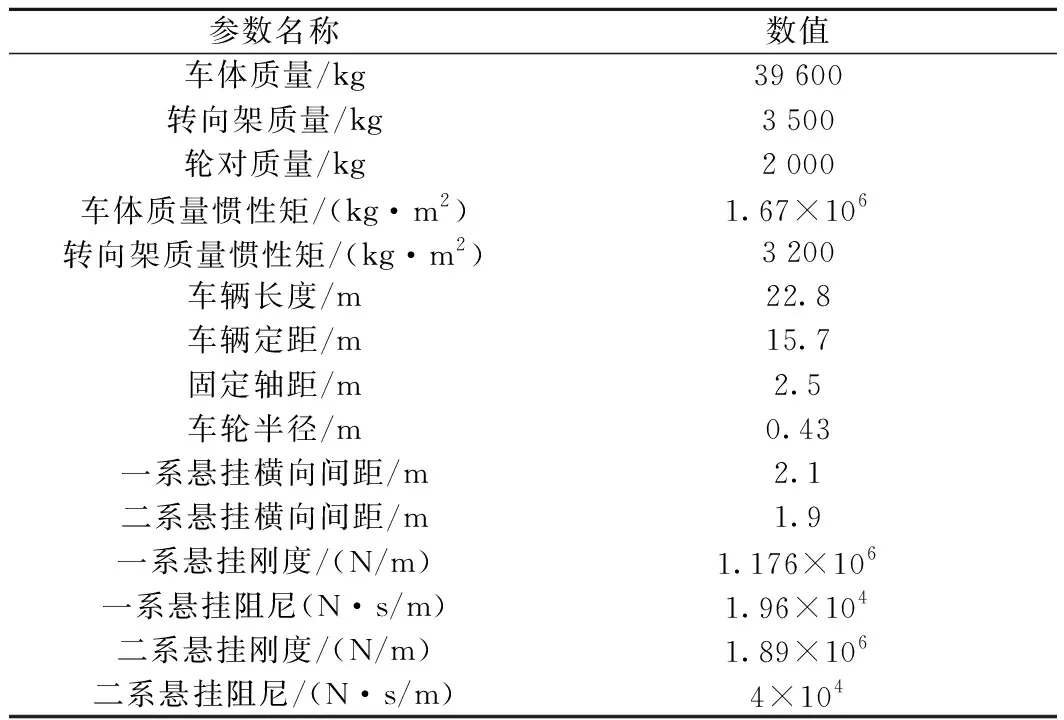
表1 车辆基本参数

图1 有限元计算模型

模型侧边与底部边界均采用无反射边界，以消除边界的波面反射，侧向边界为水平约束，底部边界为刚性约束，计算网格采用修正拉格朗日网格，其中，对靠近隧道附近网格进行加密，模型网格划分遵守波动理论中的精度要求。

1.2 模型验证

为验证上述模型的准确性，将模型仿真结果与广州地铁1号线某区间地面振动响应实测数据进行对比验证，实测与仿真计算时域与频域对比结果如图2所示。

对比图2中实测与仿真结果时域曲线可以看出，实测值与模型计算值的波形相似，加速度幅值数量级基本一致；实测结果和模型计算结果的振动主频均在50～100 Hz范围内，各频段振幅与振型基本吻合。仿真结果与实测结果差值在可接受范围内，模型仿真结果与实测结果吻合较好，验证结果表明，该模型可用于后续地铁列车运行引发的地面振动响应分析。

图2 地面振动加速度实测与仿真时域、频域对比

2 振动评价指标

为进一步分析地铁列车运行引发的地面振动情况，基于地铁列车运行引发的地面振动在垂直方向的强度要远大于水平方向的振动强度，且人们对于环境振动的感知是具有方向性的，其对于垂向振动较为敏感[18-19]，因此，主要考虑地面振动铅垂向振动分量。

根据国际标准ISO 2631和我国国家标准GB 10071—88《城市区域环境振动测量方法》中有关地铁振动研究的相关规定[20]，基于人体对各频率、各方向振动的敏感性差异，对铅锤向振动进行计权因子修正，得到修正后的振动加速度级，称为Z振级，计算式为

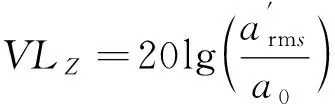
(1)

3 地面振动响应分析

为分析地铁列车运行引发的地面振动响应特性，基于上述建立的振动响应分析模型，以地铁A型车、车速60 km/h为基本工况，采用控制变量法逐个改变单一因素，分别从轨面埋深、隧道周围土层、运行车速、列车车型、减振扣件及邻近不同类型建筑物等因素影响方面，分析地铁列车运行诱发的地面振动响应特性，计算分析示意如图3所示。

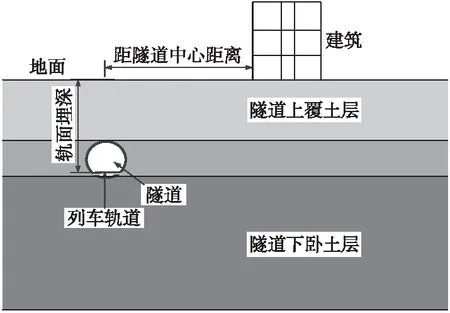
图3 计算分析示意

3.1 轨面埋深影响分析

参考广州地铁线路实际埋深情况，分别分析了轨面埋深为10，20，30 m共3种工况，计算结果如图4、图5所示。

图4 不同轨面埋深下隧道正上方地面振动加速度频谱

由图4可以看出，不同轨面埋深工况下，地面振动低频段振动加速度幅值均大于高频段；轨面埋深10 m工况时，振动加速度峰值接近5×10-3m/s2，明显大于埋深20 m及30 m工况；同时，随着轨面埋深增大，振动加速度值逐渐减小，振动频率也逐步减小，且高频部分的衰减速度较低频更快，地面振动逐步转向以低频振动为主。

由图5可以看出：在不同轨面埋深工况下，地铁列车运行引起的地面振动总体随距离呈衰减趋势，衰减程度与埋深深度成反比；在距离隧道中心20 m范围内，地铁列车运行引起的地面振动响应随着地铁隧道轨面埋深增大而减小；在距隧道20 m范围以外时，埋深10 m的地面振动快速衰减，并与埋深30 m的地面振动较为接近。

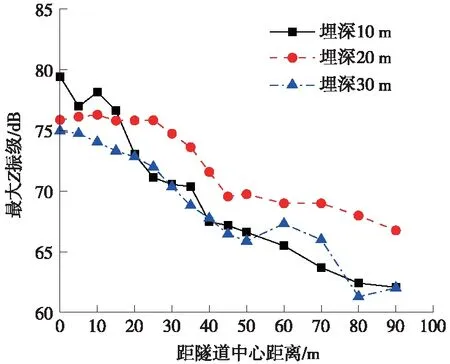
图5 轨面埋深对地面振动最大Z振级影响

3.2 隧道周围土层影响分析

广州地区地层情况复杂多样，素有地质博物馆之称，广州市地铁线路上覆土层主要为淤泥软土、砂土和粉质黏土，下卧土层主要为泥质粉砂岩，因此拟定了4种土体参数，分别定义为软土(L)、中硬土(M)、硬土(H)及岩石(R)，具体参数如表2所示。模拟浅埋隧道中(轨面埋深为20 m)土体构成并不复杂的情况下，分析不同隧道上覆土层与下卧土层组合情况对地面振动的影响，分析结果如图6、图7所示。

表2 不同土层参数

图6 不同隧道周围土层下隧道正上方地面振动加速度频谱

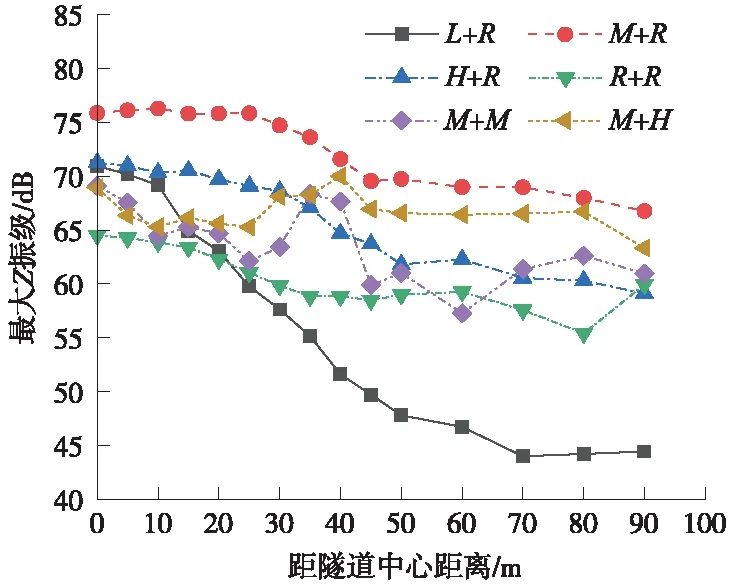
图7 隧道周围土层对地面振动最大Z振级影响

对比图6(a)～图6(c)可以看出，随着隧道上覆土层土体硬度增大，50 Hz以上频段的振动加速度幅值逐渐增大，振动逐步由低频向高频过渡；由图6(d)可以看出，当隧道所处于地段上覆岩石土层时，地面振动的高频部分振幅明显小于其他土层工况，振幅差值在1.25×10-3～1.5×10-3m/s2之间。产生这一现象的主要原因是由于隧道-土体结构的滤波作用，土体中岩石反射了大部分的振动，致使地面振动响应较小；对比图6(e)、图6(f)可以看出，在隧道上覆土层一致的情况下，不同下卧土层基本不会引起地面振动加速度频谱的变化。

由图7可以看出，当隧道上覆土层硬度达到中硬土及以上时，则由地铁运行引发的地面振动随距离衰减速率基本相同；地面振动大小与隧道上覆土层硬度呈负相关；隧道上覆土层土质为较软土时，地面振动最大Z振级随距离衰减速率最快，最大Z振级衰减幅度达25 dB；隧道下卧土层对于地面振动的影响效应小于隧道上覆土层的影响效应，在振动影响评估时需充分考虑隧道上覆土层情况。

3.3 列车运行速度影响分析

在地铁列车运行时，列车的行驶速度会对地面振动响应产生较大影响[21]，故此分析了40，60，80 km/h三种不同车速对于地面振动的影响，分析结果如图8、图9所示。

图8 不同列车车速下隧道正上方地面振动加速度频谱

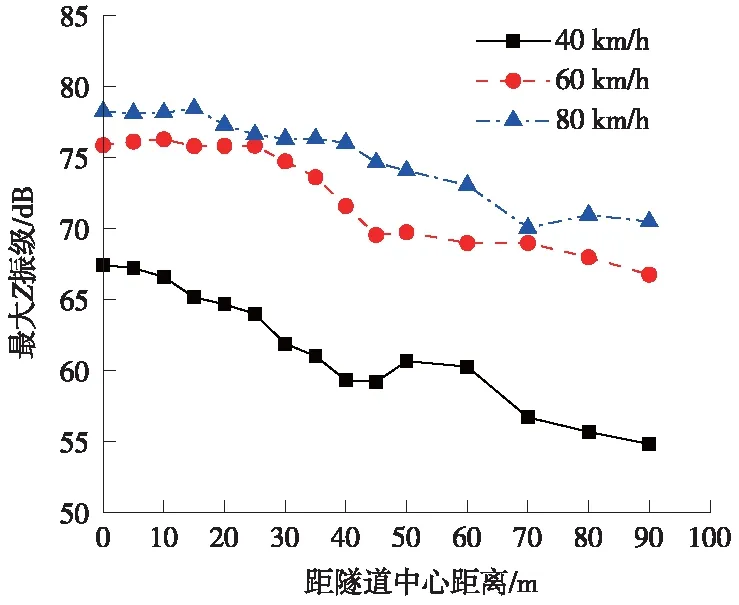
图9 车速对地面振动最大Z振级影响

由图8可知，当车速为80 km/h时，其振动加速度幅值最大，振动加速度最大值达4×10-3m/s2以上；随着列车运行速度的提升，振动加速度值逐渐增大，振动主频振幅及振动频率也逐步加大。造成这一现象的主要原因是：在同一列车情况下，随着车速提升，相邻两轴对通过同一点的时间间隔减小，致使振动频率增大[22]。

由图9可知，列车运行速度为40 km/h工况下引起的地面振动响应最小，60，80 km/h工况下的最大Z振级较为接近；由40 km/h车速提速至60 km/h时，最大Z振级增幅为8.4～12.9 dB，车速由60 km/h提升至80 km/h时的最大Z振级增幅为0.7～5.1 dB，列车车速由40 km/h提升至60 km/h时影响更加显著。

3.4 列车车型影响分析

地铁列车根据车体大小及质量等差异通常以A、B两种不同车型为主，而不同车型在运行过程中产生的振动对地面振动响应的影响也存在一定差异，为此，分析了不同车型对地面振动的影响，分析结果如图10、图11所示。

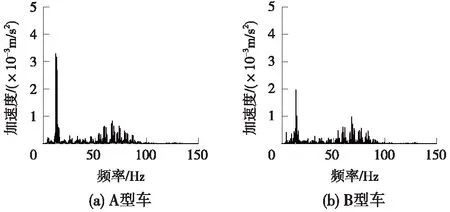
图10 不同车型下隧道正上方地面振动加速度频谱

图11 车型对地面振动最大Z振级影响

从图10中可以看出，地铁A型车运行时所引起的地面振动在低频部分的振动加速度幅值明显大于B型车工况，其振动加速度峰值接近3.5×10-3m/s2，两种车型在高频部分的振动则基本一致；对比A、B两种车型，不同列车车型仅影响到振动加速度幅值，而对振动频率方面影响较小。

由图11可知，B型车相较于A型车具有更为明显的振动放大现象；A型车运行引起的地面振动响应更为明显，相较于B型车，其产生的地面振动最大Z振级增幅在2.2～9.8 dB之间；距隧道40 m以内时，两种车型对于地面振动的影响差距较大，在进行振动分析时需重点注意该区段。

3.5 减振扣件影响分析

由于地铁列车运行所产生的振动会对周边环境产生影响，因此，在地铁建设时通常会采取一定减振措施以降低地面振动响应。故此，分析了减振扣件与普通扣件工况下地铁列车运行引起的地面振动响应情况，以此对减振扣件的减振效果进行评判，减振扣件刚度取1×107Pa。不同扣件工况下的地面振动加速度频谱及最大Z振级如图12、图13所示。

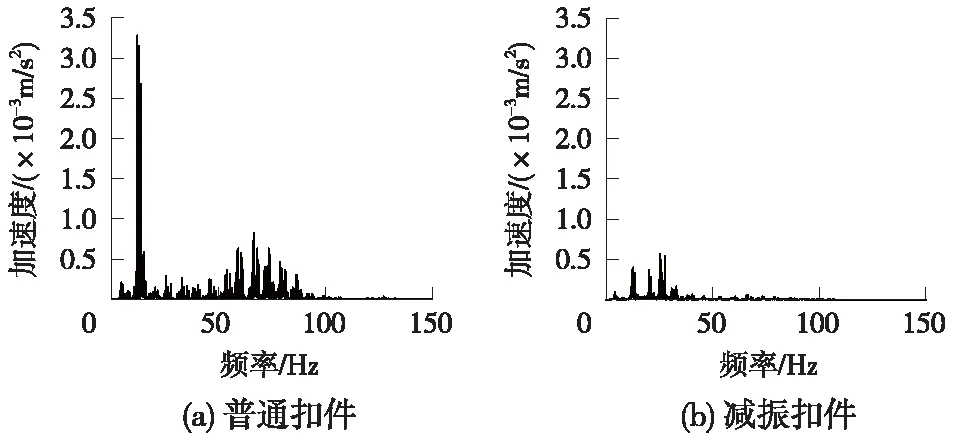
图12 不同扣件下隧道正上方地面振动加速度频谱

由图12可以看出，采用减振扣件时的地面振动加速度振幅远低于普通扣件，采用普通扣件时地面振动加速度幅值约为3.5×10-3m/s2，当采用了减振扣件后地面振动加速度幅值约为0.5×10-3m/s2，减振扣件最大减振效率达85%以上，减振效果明显；减振扣件对于地铁运行引起的地面振动具有较好的减振效果，其中，对于低频振动的减振效果更为显著。

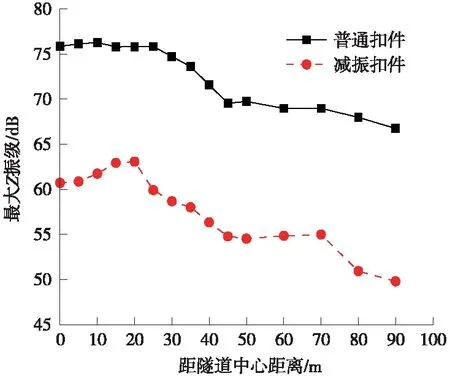
图13 减振扣件对地面振动最大Z振级影响

从图13中可以看出，对比减振扣件工况与普通扣件工况，两种扣件工况下的地面振动总体随距离增加呈衰减趋势，变化趋势基本一致，部分区段有回弹现象；减振扣件相较于普通扣件，其对于由地铁列车运行引发的地面振动具有较好减振效果，对比减振前后，减振幅度为12.7～17.1 dB，减振效果明显，长期减振效果仍需进一步验证。

3.6 建筑物类型影响分析

通常情况下，地铁沿线会存在多种类型建筑，建筑物的存在可能会对地铁运行引发的地面振动传播产生一定影响。基于此种情况，研究了距离隧道中心20 m处的3种常见的建筑类型对地铁列车运行引发的地面振动传播规律的影响，各建筑物参数如表3所示，数值分析结果分别如图14、图15所示。

表3 各类型建筑物参数

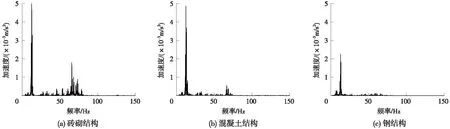
图14 建筑物所在位置处地面振动加速度频谱

图15 建筑物对地面振动最大Z振级影响

由图14可以看出，在砖砌结构、混凝土结构、钢结构建筑物3种工况下，地面振动响应依次减小，钢结构建筑物工况下的地面振动响应明显小于其他两种建筑类型；砖砌结构及混凝土结构建筑工况存在2个振动主频段，各建筑物工况下的地面振动均以低频振动为主。

由图15可以看出，在建筑物与隧道之间区段，受不同建筑物类型影响下的地面振动最大Z振级振幅基本一致，在建筑物所处位置处，钢结构建筑最大Z振级最小，混凝土与砖砌结构的最大Z振级曲线基本一致；在建筑物后方区段，最大Z振级大小关系总体为混凝土结构>砖砌结构>钢结构；不同类型建筑物基本不会影响到其所处位置之前区段的地面振动，仅对建筑物位置处及后方区段产生一定影响。

不同类型建筑物对于地面振动的衰减程度对比如表4所示。由表4可以看出，不同类型建筑物对于地面振动传播均有一定的衰减作用；其中，钢结构的衰减效果最明显，平均衰减幅度为6.7 dB。各类型建筑物对于地面振动传播的衰减效果大小为：钢结构>砖砌结构>混凝土结构。

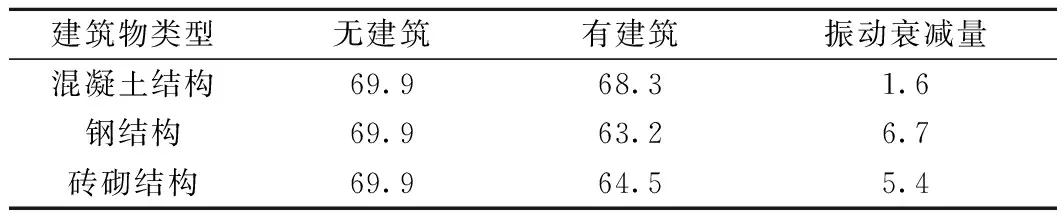
表4 不同建筑物类型地面振动衰减对比 dB

4 结论

利用ANSYS/LS-DYNA计算软件建立了振动响应分析模型，并结合广州地铁1号线实测数据，验证了模型的准确性。基于计算模型，分析了不同影响因素对于地铁运行引起的地面振动影响，得出以下主要结论。

(1)轨面埋深会对地面振动响应产生一定影响；隧道下卧土层对地面振动的影响小于隧道上覆土层的影响，在振动影响评估时需充分考虑隧道上覆土层情况。

(2)地铁列车车型与运行速度均对地面振动有较大影响，地铁A型车相较于B型车，其引发的地面振动响应更大；当车速由40 km/h提升至60 km/h时对于地面振动的影响最为显著，通过降低车速可有效减小地面振动响应。

(3)减振扣件对于地面振动的减振效果明显；建筑物对其后方地面振动传播有一定的衰减效果，各类型建筑物对于地面振动传播的衰减效果大小关系为：钢结构>砖砌结构>混凝土结构。