格库铁路风积沙包芯路基沉降数值模拟

陈桂芬,李 丽,赵加海,于 磊

(1.新疆铁道职业技术学院,乌鲁木齐 830011； 2.新疆铁道勘察设计院有限公司,乌鲁木齐 830011； 3.中铁二十一局集团第一工程有限责任公司,乌鲁木齐 830011)

引言

随着“一带一路”倡议和“十四五”规划的全面实施，我国在西北部地区修筑数条沙漠干线铁路，为国家发展战略及西部发展创造良好的交通环境，带动区域经济的发展。格库铁路东起青海格尔木，西至新疆库尔勒市，是按照国铁Ⅰ级、单线电气化铁路标准规划修建的，设计时速120 km[1]。

格库铁路S1标段位于塔克拉玛干沙漠边缘，该区域分布着范围很广的流动沙丘、半固定沙丘，由于风积沙填料具有颗粒较小、无黏结性、含水量小、保水性差的劣势，通常情况下不适合做路基填料，需采取改良措施，达到标准要求方能采用。一些学者针对高填方路基[2-3]的沉降特点及沉降的观测方法展开探讨，研究了填土高度、施工过程等因素对高填方路基沉降规律的影响；以某高速公路项目风积沙路基[4-6]施工为例，阐明在沙漠边缘条件下，采用“包边砂砾土”风积沙路基施工的关键技术；针对和若铁路的特殊气候与地质条件下路基基床底层包芯土[7]填筑施工技术原理及特点等进行总结。

许多学者就公路、铁路各种形式路基沉降的数值模拟也开展了大量的研究，取得了较多成果。杜耀辉等[8]以成武高速公路为工程依托，开展土工离心模型试验，研究泥质软岩及3种改良填料路基2年内的沉降量、沉降速率和固结时间等；赵建斌等[9]针对兰新铁路第二双线严酷的自然条件路基，研发了多点静力水准沉降观测仪，对既有的路基达到规范所要求的测试精度、频次以及评估的有效性进行研究；蔡红燕等[10-11]以某高填方路基填土开展了一维固结蠕变、三轴等室内土工试验，研究了路基填土的强度特性和蠕变特性。选取部分蠕变试验数据，通过拟合得到了蠕变模型的蠕变参数。利用ABAQUS软件建模分析，并结合现场监测数据，研究了考虑填土蠕变效应时高填方路基的沉降规律；吕绿洲等[12-13]利用Midas GTS/NX有限元软件建立黏弹性模型，通过数据拟合得到模型参数，从而对路基最终沉降进行预测；何文春[14]运用数值模拟了合肥至福州高速铁路采空巷道上方车站桩板路基的变形规律；徐子超等[15]采用ABAQUS软件建立了土拱效应产生与退化的弹塑性三维有限元模型，对桩承式路堤的土拱高度进行了分析，并研究桩间距、填土强度等因素对土拱高度的影响；李小娟等[16]为定量分析铁路路基沉降的各个因素对沉降值的影响程度，提出了一种基于神经网络的路基沉降因素敏感度分析方法，采用均匀设计法将各沉降因素的不同取值进行组合，形成相应的工况，并以ANSYS软件计算每一组工况下的路基沉降量，得出敏感度分析的样本数据；李成等[17]运用大型通用有限元软件ABAQUS，针对内蒙古G210线查干段改线工程，对该工程的路基路用性能进行了数值模拟研究，分析路基在实际荷载作用下的水平和竖向变形；王永松[18-19]采用MIDAS GTS有限元软件，建立软土--路堤二维平面模型，研究路基的填筑高度、填筑速率和排水效果对软土路基沉降的影响程度；柳斌[20]依托某二级公路高边坡路基施工项目，利用有限元分析软件ABAQUS和理正岩土分析软件，分别对施工项目中涉及到的高边坡路基进行稳定性计算，并对比验证准确性；张兴鑫等[21]基于CFD数值模拟，以青海省中灶火省道303公路为研究区域，对流动沙丘区公路路基风沙流场进行了模拟分析，揭示了流动沙丘区路面沙害的形成机制；李浩霖等[22]通过Midas GTS有限元软件，建立填方路基截面数值模拟，模拟了在填土高度、路基坡度、填料和压实度等因素作用下填方路基的沉降情况；魏瑶等[23]采用有限元软件模拟动态变形模量的测试过程，分析承载板与土体接触压力、路基动态变形模量等影响因素，并计算动态变形模量的有效测试深度；徐宏等[24]基于正交试验设计，运用MIDAS GTS/NX有限元软件计算不同试验水平组合的边坡安全系数，边坡稳定影响因素敏感性从大到小依次为坡高、黏聚力、坡比、内摩擦角、重度、弹性模量、泊松比等。

上述文献主要是针对高填方路基、包芯路基的施工技术和不同类型的路基沉降进行数值模拟展开研究，而针对包芯路基各部位沉降的模拟鲜见，鉴于此，利用有限元软件Midas GTS，选取塔克拉玛干沙漠边缘风积沙的物理参数——内摩擦角、弹性模量和泊松比进行数值模拟，模拟出不同参数变化时路基各部位变化的位移云图，以期对线路开通运营后路基的养护维修提供理论依据和数据支持。

1 工程概况

格库铁路S1标段路基首件工程位于DK1094+300～DK1094+600段，直线，长度为300 m，该标段地处塔克拉玛干沙漠边缘，大部分是以填方形式通过，占总土方量的92%以上，路基填料以细角砾砂、细砂和风积沙为主。线路两侧沙料较充足且距离料场较近，设计时采用风积沙包芯路基填筑形式。施工时“芯”就近取材，采用检验合格的C组风积沙、粉土填料；两侧和基床表层分别采用远距离运来的B组和A组填料“包边加固”，确保路基的稳定性。该段路基基底主要为风积沙、粉砂以及细砂，基床以下路堤最大填筑高度为6.24 m，最小填筑高度为3.70 m，平均填筑高度为4.97 m，而且路基边坡坡比需满足路基稳定性要求，设计要求的边坡坡比为1∶1.75。

依据设计要求，路堤基床表层采用规范规定的A组填料，高度为0.6 m；基床底层芯部采用C组填料(风积沙、粉砂填料)，高度为1.9 m，两侧包边加固填料为B组填料，包边宽度为2.0 m；C组填料同样用于基底以下部分填筑。在基床底层顶部、底部铺设土工格栅，可以防止水分蒸发，增强路基稳定性。包芯路基设计断面如图1所示。

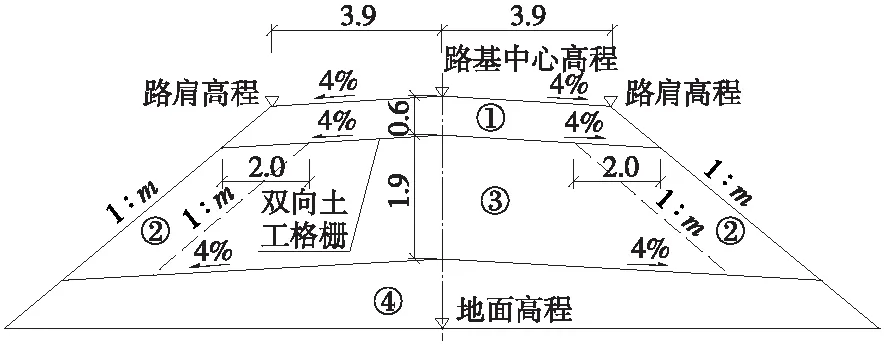
图1 试验段路基填筑横断面示意(单位：m)

图1中:①—基床表层；采用A组填料；②—基床的底层；包边材料采用B组填料；③—基床的底层；包芯部分采用C组填料；④—基床以下；采用C组风积砂填料。

根据施工单位土工试验室对沙漠地区试验段基底不同深度选取的沙样进行试验，得出不同组沙样填料的最佳含水量和最大干密度，其中A组填料：ρdmax=2.25×103kg/m3，ω=8.2%；B组填料：ρdmax=2.24×103kg/m3，ω=8.6%；C组填料：ρdmax=1.71×103kg/m3，ω=11.6%。风积沙的细粒组含量和黏粒含量的差异引起风积沙的最大干密度和最优含水率的差异，细粒组含量越多其压实性能越好。

取该地区沙样通过试验得出，内摩擦角一般处于29°～44°范围内，不同深度基底风积沙的内摩擦角会存在差异；压缩模量处于44～70 MPa范围内；泊松比在0.25～0.35之间。

2 风积沙包芯路基计算模型

在道路工程分析中，有限元法综合分析了路基和路堤，它把路堤、路基看作一个整体来划分网格，计算过程中进行离散，形成离散体系，并且可以计算在给定荷载作用下的位移与应力。有限单元法主要采用非线弹性、弹塑性等模型，建立土体本构关系解决相关问题。本文采用有限元软件Midas GTS/NX进行数值模拟。

2.1 数值模拟路基沉降分析步骤

按有限元分析思路和方法，对路基沉降进行有限元分析的具体步骤见图2。

图2 路基沉降有限元分析流程

2.2 计算区域及参数的选取

根据路基填筑示意图确定DK1094+600断面数值模拟计算模型如图3所示。

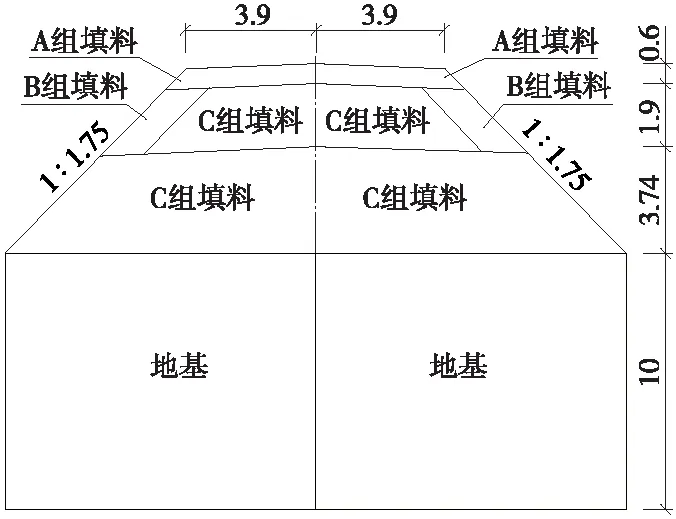
图3 DK1094+600断面数值模拟计算模型(单位：m)

2.3 计算加载方案

采用TB 10001—2016《铁路路基设计规范》标准列车荷载进行计算，同时将列车本身的重力及其运行过程中产生的力考虑在内，将列车荷载利用换算土柱法简化为静荷载处理，使其以均布荷载的形式施加在道床之上，并考虑相应的应力扩散，即用与填筑路基土体重度相同的土柱来代替路基面上的列车和轨道荷载的合力，如图4所示。

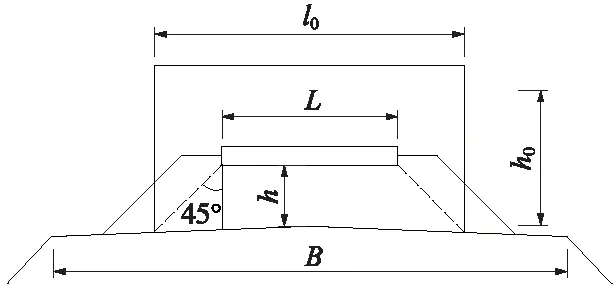
图4 列车荷载简化计算图示

换算土柱高度

(1)

式中h0——路基顶面上换算土柱高度，m；

l0——换算土柱作用宽度，m；

l0=L+2h·tan45°=L+2h，h为道床厚度，m，L为轨枕长度，m；

γ——路基填土重度，kN/m3；

P——每延米作用在路堤上的列车和轨道荷载，kN/m。

根据取样试验，土体容重为19 kN/m3，换算土柱高度取3.2 m。

2.4 模型本构关系的选取

模型建立时，土工格栅在土体作用中所受拉力远小于其抗拉强度，因此将土工格栅的本构关系取为线弹性，其应力应变关系呈线性。岩土材料采用弹塑性构建模型，即在未达到屈服点以前，其应力与应变的关系是呈正比例的，而在超过屈服点时，应力-应变关系曲线是呈水平的。屈服准则采用摩尔-库伦准则。

2.5 单元类型的选取

本模型中土体采用平面应变单元，同时对土工格栅采用相应的土工格栅单元。

(1)平面应变单元

选取平面四边形单元对岩土体进行模拟。

平面应变单元的平衡方程如下

(2)

式中L——单元边界长度；

t——单元厚度，取1；

u——单元插值函数(关系)；

B——应变矩阵；

D——弹性矩阵；

BT——应变转置矩阵；

dA——单元面积的单位面积积分函数；

N——单元形函数矩阵;

Nt——单元面积形函数转置矩阵;

NT——单元长度形函数转置矩阵;

Pn——单元节点力(荷载)矩阵。

平面应变单元的应变采用以下公式计算

(3)

平面-位移几何方程如下

(4)

雅克比矩阵如下

(5)

二维应变单元数值积分变换如下

(6)

其中，W1j，W2j分别为积分点的ξ，η方向上的权重。

(2)土工格栅单元

在Midas GTS/NX中土工格栅单元采用薄膜单元(只有抗拉强度而没有抗弯能力的薄膜单元，只能产生轴向的变形)。采用四节点薄膜单元来模拟，其形函数如式(7)所示。

Ni=(1+ξiξ)(1+ηiη)/4(i=1，2，3，4)

(7)

应变、单元局部坐标下的节点位移列阵计算公式分别为

{ε}e=[B]{δ}e=[B1B2B3B4]{δ}e

(8)

{δ}e=[D]{ε}e=[D][B1B2B3B4]{δ}e

(9)

式中

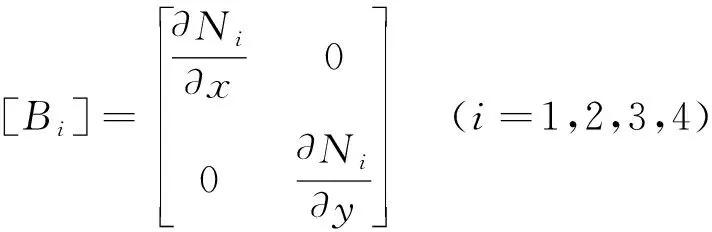
(10)

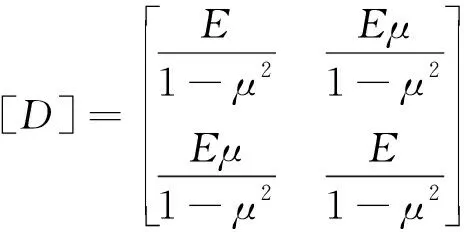
(11)

式中 [Bi]——几何矩阵；

E——弹性模量；

μ——泊松比;

[D]——弹性矩阵。

经过上述理论计算分析，针对沙漠铁路路基DK1094+600处断面采用Midas GTS/NX模拟时，采用单元长度为0.5 m的自动网格三角形划分方法，模型见图5。

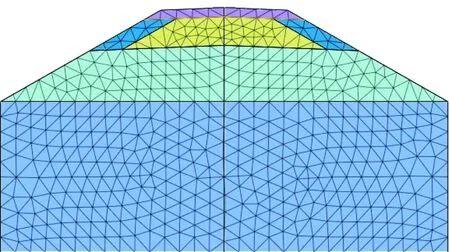
图5 优化处理后的路基模型

3 基于数值模拟包芯路基沉降量影响因素分析

运用Midas GTS/NX软件，研究基底风积沙填料的内摩擦角、弹性模量和泊松比等参数对沙漠铁路路基沉降量的影响和变化趋势。

3.1 内摩擦角的影响

根据现场试验得出S1标段风积沙填料的内摩擦角一般处于29°～44°范围内，模拟不同内摩擦角的位移云图，见图6。

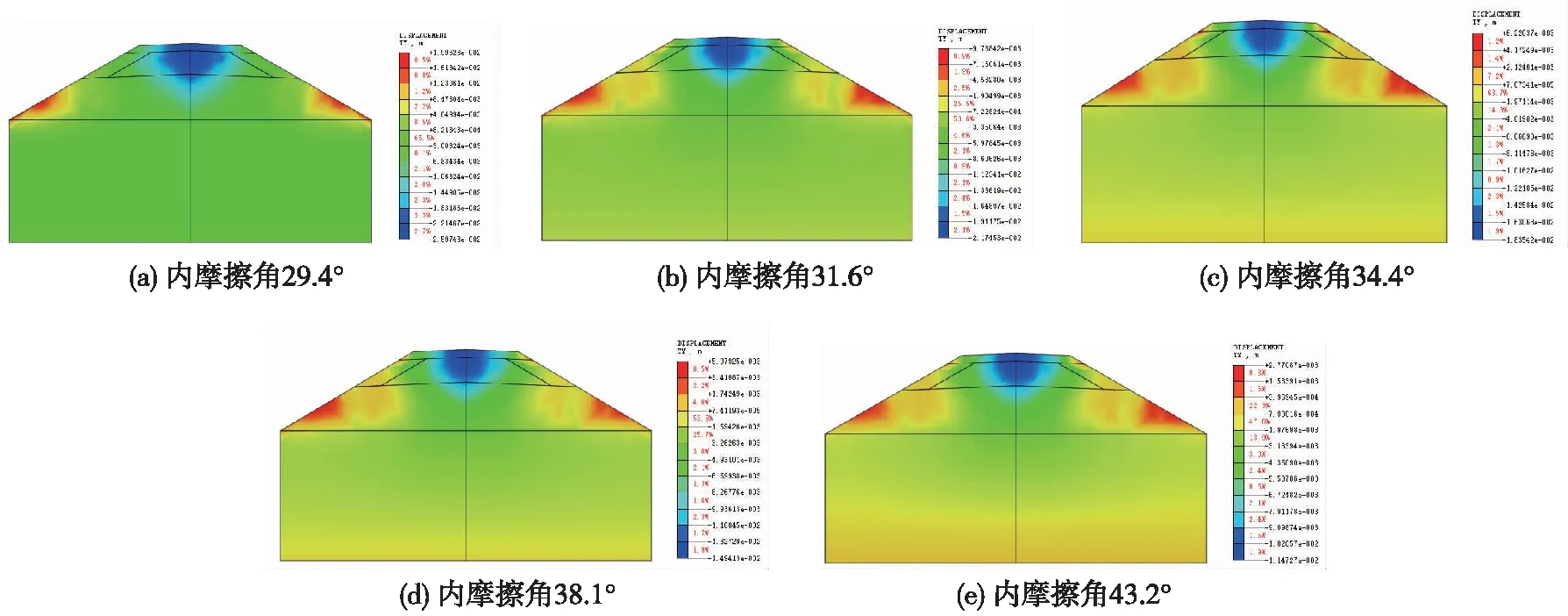
图6 不同内摩擦角DK1094+600断面位移云图

由图6选取不同内摩擦角路基各主要部位的位移值，得出不同内摩擦角对路基变形的影响，如表1所示。

表1 不同内摩擦角对路基变形影响

由图6和表1数据得出:内摩擦角为一确定值时，包芯部位沉降量最大；随着内摩擦角的增大，路基各部位的位移值在减小。在路基两侧边缘有隆起现象，两侧中部、基底及以下位移量变化较小。取不同内摩擦角包芯部位、两侧中部、基底及以下的沉降量，见图7。

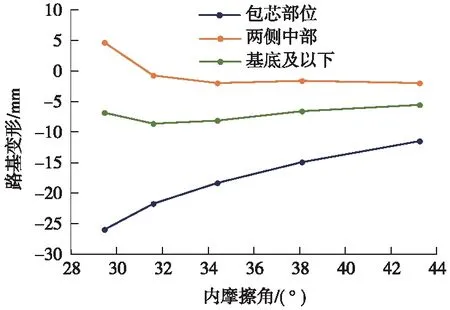
图7 内摩擦角与包芯部位沉降关系曲线

由图7可知:风积沙填料内摩擦角增大时，路基芯部最大沉降量出现明显减小的趋势，二者为非线性关系。随着压实度的增加，填土层内摩擦角有一定增加，进而使得路基沉降量有减小的趋势。风积沙内摩擦角是影响路基沉降变形的较大因素，表现为内摩擦角与路基沉降量呈反比。

3.2 弹性模量的影响

依据试验，基底风积沙填料压缩模量为44～70 MPa，根据弹性模量与压缩模量的换算关系，其弹性模量取值范围为89～110 MPa，将风积沙弹性模量分别赋值为89，95，100，105，110 MPa，模拟风积沙不同弹性模量的位移云图，见图8。

由图8选取土体不同弹性模量在路基各主要部位的位移值，得出表2数据。

表2 土体不同弹性模量对路基变形影响

由图8、表2可以得出：当弹性模量为一定值时，包芯部位沉降量最大；随着弹性模量的增加，路基各部位的变形量在减小。路基两侧有微微隆起，两侧中部、基底及以下部位沉降量较小，而且变化量也很小。取不同弹性模量包芯部位、路基两侧中部、基底及以下的沉降量，见图9。

图8 不同弹性模量DK1094+600断面位移云图

由图9可知：风积沙填料的弹性模量变化对路基包芯部位最大沉降量影响很大。当砂土层弹性模量较小时路基的承受变形的能力也小，因此荷载引起的沉降量较大；在其他条件不变的情况下，随着基底层弹性模量的增大，承受变形能力也不断提高。

图9 弹性模量与包芯部位沉降关系曲线

3.3 泊松比的影响

其他条件不变时，根据现场试验得出的泊松比在0.25～0.35之间，模拟不同泊松比的位移云图，见图10。

根据图10可以看出路基不同部位的位移情况，选取不同泊松比路基各主要部位的位移列于表3。

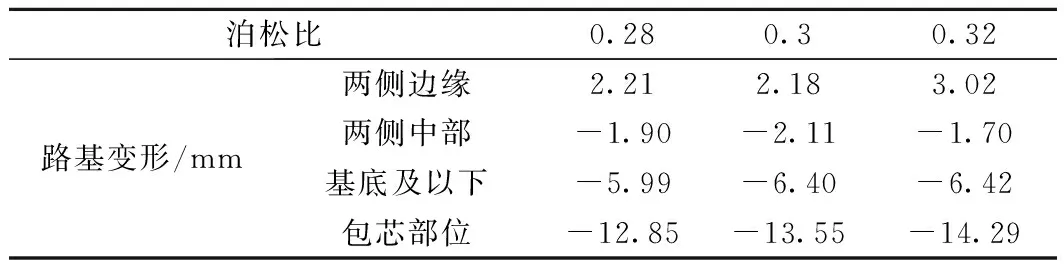
表3 泊松比对路基变形影响

图10 不同泊松比DK1094+600断面位移云图

由图10和表3可知：风积沙填料泊松比对路基沉降变形具有一定的影响。当泊松比一定时，包芯部位的沉降量最大；在其他条件不变的情况下，随着风积沙沙样泊松比的增加，路基各部位沉降有增大的趋势，即引起的地层损失越来越大；路基两侧边缘也有微微隆起现象，两侧中部、基底及以下沉降量较小，变化也很小。

4 结论与建议

通过利用Midas GTS/NX软件模拟在标准列车荷载作用下，风积沙包芯路基各部位在内摩擦角、弹性模量和泊松比变化的位移云图，得出以下结论。

(1)在3个参数允许变化范围内，内摩擦角对路基沉降影响最大，弹性模量次之，泊松比最小。

(2)随着内摩擦角和弹性模量的增加，包芯部位、基底及以下的沉降量有减小的趋势；而随着泊松比的增加，包芯部位、基底及以下的沉降量有增大的趋势。

(3)路基两侧中部变形量很小，两侧边缘有微微隆起现象。

(4)基底及以下沉降变化较小，说明土工格栅发挥了作用。

建议：本次模拟的是单个参数变化的位移云图，是较理想的状态。格库铁路开通运营后，受多种因素影响，在列车动荷载作用下风积沙包芯路基各部位受力情况更为复杂，还有待于长期监测，探究其沉降变化规律。