顺应“深度学习” 变式拓展探究
——以一道圆锥曲线高三质检试题的变式探究为例
山东 黄绪荣
由美国新媒体联盟和美国学校网络联合会合作完成的2015年基础教育《地平线报告》提出了两种长期趋势,其中一种就是探索深度学习的策略.深度学习就是在教师的引导下,学生围绕具有挑战性的学习主题,全身心参与、体验成功、获得发展的有意义的学习过程.复习课是高三数学教学的常态,承载着知识的再现与深化、方法的总结与凝练、思想的感悟与提升.由于解题教学是高三复习课教学的主体形式,发展学生数学分析和表达能力,促进学生思维的纵向深入发展,引导学生深度学习,应当成为倡导提升数学素养的高三解题教学的价值追求.基于“深度学习”理念,在对2022年2月福建省漳州市2022届高三毕业班第一次教学质量检测数学试题第21(2)题的深度探究、发现过程中,从解法探究,到延伸推广,再到类比拓展,直到最后发现圆锥曲线的性质,整个过程可以说完全基于并顺应了“深度学习”理念,是一次基于“深度学习”理念探究问题的收获尝试.现将整个探究过程展现出来与诸位同行分享、交流.
一、试题呈现

(1)求Γ的方程;

二、解法探究
对于第(1)题,先利用三角形面积公式变形已知面积等式,再利用双曲线定义和性质求得a2,从而得到Γ的方程.
解:设△PF1F2的内切圆半径为r,






又a2=c2-1,解得a2=3,

对于第(2)题,解答的关键是求切线l的方程.按常规解法,首先设出切线l的方程,然后与双曲线方程联立、变形整理,利用判别式为零和点P在双曲线上得到的坐标间的整体关系,将l的斜率表示为点P的坐标关系,进而变形l的方程,最后表示出两个交点M,N的坐标,运用两点间的距离公式和点P在双曲线上得到的坐标间的整体关系,证得等式.
这个解题程序是清晰、明确的,但实际解答中,其式子、方程之复杂、运算量之大,困难程度是出乎想象的.
解法1:由题意可知直线l不垂直于x轴,设l的方程为y-y0=k(x-x0),所以y=k(x-x0)+y0.

得x2-3[k(x-x0)+y0]2-3=0,
所以x2-3(kx-kx0+y0)2-3=0,



面对这样一个含有多个参量的关系,不知后面的关系会有多么的复杂,至此,信心顿失、难以为继,因运算受阻而就此搁置!
仔细想想,第(2)题的“梗”在于求切线l的方程.这样我们可以转换一下对解题认知的思路,运用双曲线的“二级结论”直接给出切线l的方程,然后完善解答,虽然此做法得不到该题的满分,但至少可以得到大部分的分数,比放弃解答要强很多.这里将解法1后面的解题过程补充完整,就可以感觉到搁置解法1是个明智的选择.



因为P(x0,y0)是Γ右支上一点,




所以(x0-3ky0)2=0,所以x0-3ky0=0.

所以代入l的方程为y-y0=k(x-x0),













下同解法1.
这里需要进一步提醒的是,数学中的许多“二级结论”可以直接用来解答客观题,但用于解答主观题时必须有推证的过程,其实上面的解法1运算受阻的原因就在于所用“二级结论”的推证过程.
除上面的两种解法外,第(2)题还有没有更好地解答途径呢?我们进一步转换视角,可以从“点P(x0,y0)是Γ右支上一点”和“在点P处的切线l”这两点切入来考虑,将Γ右支分上半支和下半支来讨论的基础上,利用导数的几何意义解答,岂不妙哉!于是,就有了下面我们优选的解法.
解法3:由题意可知直线l不垂直于x轴,设l的方程为y-y0=k(x-x0).

由题意知y0≠0,













下同解法1.
三、考查模式
(1)求C的方程;

其中第(2)题就是以双曲线为载体的定值问题.
求解定值问题的基本思想是函数思想,可以用变量表示问题中的直线方程、数量积、比例关系等,得到问题所需要的代数表达式,然后对表达式进行直接推理、计算,并在推理计算的过程中消去变量,从而得到定值.这种方法可简记为:一选(选好参变量)、二求(对运算能力要求颇高)、三定值(确定定值).
四、试题变式
1.变式思考,延伸推广
思考第(2)题证得的结论,有下列两个变式问题:
变式1.若点P在Γ的左支上将会是怎样的?结论与点P在Γ的右支还是左支上有无关系?
变式2.点A能否在其他象限的渐近线上或不在渐近线上?结论与点A是否在Γ的渐近线上有无关系?


证明:由题意可知直线l不垂直于x轴,设l的方程为y-y0=k(x-x0).

由题意知y0≠0,












所以b2x0x-a2y0y=a2b2.





故证得|MF2|=e|NF2|.

按结论1的证明过程同理可证得.
2.类比变式,结论深化
圆锥曲线有许多相似的性质或结论,于是又有:
变式3.将结论1和结论2分别类比变式到椭圆和抛物线,是否有同样的结论?
经过一番探究发现,答案是肯定的,于是就有了椭圆和抛物线的3个结论.

证明:由题意可知直线l不垂直于x轴,设l的方程为y-y0=k(x-x0).
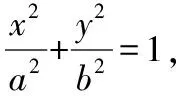
由题意知y0≠0,













所以直线l的方程为b2x0x+a2y0y=a2b2,





故证得|MF2|=e|NF2|.

按结论3的证明过程同理可证得.

证明:由题意可知直线l不垂直于x轴,设l的方程为y-y0=k(x-x0).
由题意知y0≠0,











故证得|MF|=|NF|.
3.整合变式,收获共性
变式4.以上分别得到了三种圆锥曲线的结论,能否将上述5个结论进行整合、统一呢?
于是经过探究,我们得到了一般圆锥曲线的一条性质命题:圆锥曲线Γ的一个焦点为F,离心率为e,点P是Γ上一点,若Γ在点P处的切线l与过F且垂直于x轴的直线相交于点M,与F相应地准线相交于点N,则无论点P怎么变动,总有|MF|=e|NF|.
五、教学感悟


