寻根求源探本质 变式教学促发展
——以2022届“江南十校”高三一模联考文科数学17题为例
安徽 李多猛 张 刚
区域性高三联考通常是一个地区(或若干个地区)的高中联盟体,为了提升本地区高三复习备考的教学质量,检测高三师生复习效果的一种大型考试.通过各地区示范性高中联盟理事会轮流组织命题考试,集中试卷批改和分析,实现对联盟体内各高中教学质量进行评估和指导.因此,这种区域性联考具有很强的教学引领和风向标作用.
2022年3月7日至8日,联盟体——“江南十校”组织了区域性高三一模,本次数学试卷具有较好的区分度,试卷命制质量也比较高,通过阅卷发现学生的一些典型答题错误,失分实属可惜.下面笔者以2022届“江南十校”高三一模联考文科数学17题为例,谈谈自己在试卷讲评课中的一些新尝试,希望能给后期的高三数学专题复习带来一些参考和建议.
一、原题再现

(1)求数列{an}的通项公式;

当n≥2时,an=Sn-Sn-1=n2+2n-[(n-1)2+2(n-1)]=2n+1,
a1=3也符合上式,故an=2n+1.




二、试题分析
1.总体评价
本题主要考查数列的通项与数列的前n项和的关系以及“差比型”数列的前n项求和,主要考查逻辑推理、数学运算等数学核心素养.以下是宿州市城区三所示范高中参加考试的1 181名文科学生的答题得分统计分析表:

题号实考人数满分值平均分标准差得分率难度区分度第17题1 181127.943.450.660.660.45
从统计结果看,本题答题情况并不好,尤其是第二问的错位相减求和,人人能做,但能最终答对的却不多.考后笔者统计了学生在用错位相减法求和时的常见错误类型:
(1)符号错误;
(2)指、系数书写错误;
(3)指、系数运算错误;
(4)书写不规范等.
2.错因探源
从考后的统计结果可以看出学生对错位相减法求和的整体过程模糊不清,主要体现在相减之后的等式中的等比数列求和的项数模糊不清;对等比数列前n项和公式理解不透、运用不熟,导致运用公式求和时出错;思维定式将最后一项的符号简单对应项数符号,同时数学基本运算能力的欠缺也是出错的一个重要原因.
3.解决策略
错位相减法求和在一定程度上具有程序化的特点,因此规范书写格式(一般为“前三后二”,上下对齐的是同类项)是减少错误的有效途径,如下所示.

其次,要注意确认最后一项的符号以及中间等比数列求和的项数是否正确,正确使用求和公式运算.最后,还要学会检验,对于用错位相减法求得的结果Tn,可根据T0=0,T1等于首项检验求得的Tn是否正确.
三、探寻本质
“错位相减法”是在推导等比数列前n项和公式时采用的经典方法,也是求“差比型”数列前n项和的常用方法,主要考查逻辑推理和数学运算核心素养.一直以来,用“错位相减法”求“差比型”数列前n项和似乎是“教师教、学生学”的唯一选择,但也一直是老师的痛处、学生的伤点!还有没有求“差比型”数列前n项和的其他路径和选择呢?以下是笔者在评讲该题的课堂教学新尝试(片段).
师:问题的本质是什么?

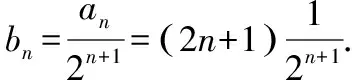
生:把数列的前n项相加,即Tn=b1+b2+…+bn.
师:数列{bn}的前n项和与通项bn有何关系?
生:bn=Tn-Tn-1(n≥2).
师:很好,这样通项bn就可以看成函数Tn与Tn-1的差,
也就是说Tn=T1+(T2-T1)+(T3-T2)+…+(Tn-Tn-1),能否考虑像这样先把bn裂项,再求和?(学生开始议论)
生:函数Tn怎么找?(学生感觉为难)
生:两个函数的乘积.
师:两个什么函数?

师:任意两个线性函数的差是什么函数?
生:还是线性函数.(学生都被这样的“问题串”吸引住了,不少学生紧锁的眉头也慢慢舒展了)
师:bn-bn-1等于什么?结果与通项bn比较有何特征?


师: 非常好!(学生思维的火花被点燃了)
四、深度挖掘



使bn=f(n)-f(n-1),n∈N*,



所以Tn=b1+b2+…+bn
=(f(1)-f(0))+(f(2)-f(1))+…+(f(n)-f(n-1))
=f(n)-f(0)
五、通法探究
数学是思维的科学,发展学生数学核心素养离不开数学思维能力的提升,课堂教学中,教师的任务就是通过引导学生发现和提出问题、分析和解决问题,从而培养学生良好的逻辑推理能力.波利亚在《数学的发现》中提出,高中数学课程教学目标首先和主要的是:“必须教会那些年轻人思考.”所以课堂教学不但要以问题为起点,还要以进一步的问题来推进,引领学生深度学习.到此为止,学生是不是真正把问题的本质解决了呢?笔者认为,学生的思维训练还远远没有结束,可以再进一步引导学生思考此类问题的通法.
【例1】已知数列{cn}的通项公式为cn=(An+B)·qn(A,B为常数,q≠0且q≠1),求数列{cn}的前n项和Tn.
解析:令f(n)=(kn+b)·qn且cn=f(n)-f(n-1),n∈N*,则由
(An+B)·qn=(kn+b)·qn-[k(n-1)+b]·qn-1,消去qn-1得,
(An+B)·q=(kn+b)q-[k(n-1)+b]=(kq-k)n+bq-b+k,
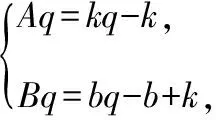

Tn=c1+c2+…+cn
=(f(1)-f(0))+(f(2)-f(1))+…+(f(n)-f(n-1))
=f(n)-f(0).
事实上,若数列{cn}的通项是由关于n的多项式函数与关于n的指数函数的乘积构成,即cn=[ak·nk+ak-1·(n-1)k-1+…+a1·n+a0]·qn,则都可以采用“待定裂项法”求数列{cn}的前n项和,这样问题就迎刃而解,学生的解题思路也豁然开朗,解答问题自然水到渠成.
六、变式教学
在后期高三数学专题复习教学中,引领学生掌握解题方法和规律,更多的是通过数学问题的变式应用来实现,从而加深学生对知识内涵与外延的真正理解,真正实现掌握问题本质,这对于高三数学冲刺阶段的复习可以起到事半功倍的作用,同时也能提高学生对数学问题的梳理和归类,把握一类问题的规律,实现通法通解,以不变应万变,提升数学核心素养.因此,数学专题复习教学中,还可以尝试对上述母题改变条件或结论,下面略举一例说明.
【变式1】已知数列{cn}的通项公式cn=(n2+n-2)·2n,n∈N*,求数列{cn}的前n项和Tn.
解析:令f(n)=(an2+bn+c)·2n,
且cn=f(n)-f(n-1),
则(n2+n-2)·2n=(an2+bn+c)·2n-[a(n-1)2+b(n-1)+c]·2n-1,
即2n2+2n-4=2(an2+bn+c)-[a(n-1)2+b(n-1)+c]=an2+(2a+b)n-a+b+c,

所以f(n)=(2n2-2n)·2n=n(n-1)·2n+1,n∈N*,
Tn=c1+c2+…+cn=f(n)-f(0) =n(n-1)·2n+1.
现代认知心理学家认为,数学学习是个体认知结构从建立到扩展,再到精致的过程.上述问题就是母题条件中的特殊化、具体化的表现,考查学生对数学问题本质的理解.通过母题变式教学,要引领学生深度学习,实现学生对数学问题本质特征结构的把握,教师还可以继续实施变式题组教学,比如母题逆命题是否成立等,从而实现学生举一反三,触类旁通的教学效果.
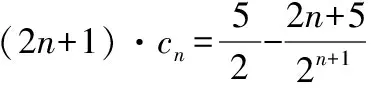



……
改变问题的结构、形式,更换问题的条件和结论,以及探寻问题的一般化规律等,都是为了进一步揭示数学问题本质,帮助学生多角度、多层次理解知识,培养学生在不同条件下迁移、发散能力、建构知识体系能力的过程,也是促进学生由“知识型”向“能力型”转变的过程,从而发展学生的数学核心素养.当然,教师还可以结合自己的实际课堂需求,继续实施类似变式的题组教学,这里限于篇幅,不再一一赘述.
七、教学反思
1.积极提升自身专业素养
实践数学核心素养的课堂教学除了教材中明确的知识技能目标外,还应该包含数学知识的本质、发展的过程、体现的思想和与其他知识的联系等,因此,教师要积极提升自身专业素养.只有教师对数学知识产生、发展过程全面了解,才能恰到好处地点拨和引导学生暴露问题本质,还原问题本真;只有教师对数学问题的思想和方法深入体会,才能引领学生深度学习,学会用数学思维思考.
2.重视知识体系建构联系

3.加强引领学生变式教学


