误差齿面下直齿轮副内部激励及动态特性分析
刘 昶,石万凯,刘 坤,刘 浩
(重庆大学 机械传动国家重点实验室,重庆 400044)
近年来随着电动汽车的普及,对齿轮传动系统振动噪声性能要求明显提高。齿轮传动系统作为一种参数自激系统,即使不受外部激励的影响,在内部激励的作用下,系统也会产生自激振动[1]。时变啮合刚度和综合啮合误差是齿轮系统最重要的内部激励[2]。因此,精确计算齿轮系统的时变啮合刚度和综合啮合误差,并在此基础上研究各类型误差对齿轮系统动态特性的影响规律,对预估和控制齿轮系统振动噪声水平具有重要意义。
国内外学者已就齿距累积偏差[3]、齿廓偏差[4-5]、裂纹故障[6]、齿面微观形貌[7]等对齿轮传动系统动态特性的影响开展了广泛研究。现有研究中,时变啮合刚度的计算方法通常可分为有限元法和解析法两大类[8]。有限元法因其计算结果精确而被广泛接受和应用[9]。Yuan等[10]和Ma等[11]通过有限元方法分别研究了载荷和齿廓修形量对时变啮合刚度的影响。随着计算机技术的发展,尽管有限元法已在各个领域得到广泛应用,但在计算齿轮时变啮合刚度方面仍存在一些不足。一方面,有限元法的计算精度与网格质量有关,通常为了提高计算效率、降低计算成本,网格尺寸很难达到微米级,难以模拟齿轮加工误差对时变啮合刚度的影响;另一方面,为了简化有限元模型,通常仅考虑齿轮副中的部分齿对,而每个轮齿的加工误差不同,忽略了轮齿啮合次序对时变啮合刚度的影响。
相较于有限元法,解析法具有更高的计算效率,且其计算结果与有限元法计算结果一致性较好,因此近年来受到越来越多的关注。解析法中常用的有材料力学方法[12]和弹性力学方法[13],但它们主要用于单齿刚度及单齿啮合刚度的计算问题,而多齿啮合时,常通过将单齿啮合刚度简单叠加得到。此外,在动力学分析时,多以理想齿轮为对象,计算其时变啮合刚度,忽略了齿轮实际啮合过程中,由加工、安装误差导致的轮齿脱啮、线外接触和偏载等一系列非正常啮合现象对时变啮合刚度的影响。
在齿轮动力学分析时,许多学者[14-16]采用简谐函数模拟齿轮综合啮合误差,且其幅值通常采用假设的方式或根据齿轮精度等级对应的公差值确定。然而,不同类型齿轮误差导致的综合啮合误差波形和幅值差异较大。此外,齿轮综合啮合误差与时变啮合刚度二者深度耦合,仅用简谐函数模拟齿轮综合啮合误差而不考虑对时变啮合刚度的影响,难以得到较为精确的动力学分析结果。
基于上述原因,本文首先建立了考虑齿轮加工、安装误差的误差齿面模型,提出了适用于该误差齿面模型的承载接触分析算法,并对直齿轮副的时变啮合刚度和综合啮合误差进行了精确计算。在此基础上,建立了直齿轮副弯扭耦合动力学模型,研究了不同类型误差对齿轮传动系统动态特性的影响规律。
1 误差齿面模型
为建立误差齿面模型,首先将直齿轮齿面离散,如图1所示。渐开线齿轮左右齿面分别被离散为n1×n2个相同大小的单元,各离散单元被近似为具有不同曲率半径的圆柱面。假设每个离散单元具有一个控制点,且该控制点位于离散单元的中心,并通过索引i和j定义控制点在齿面上的编号。
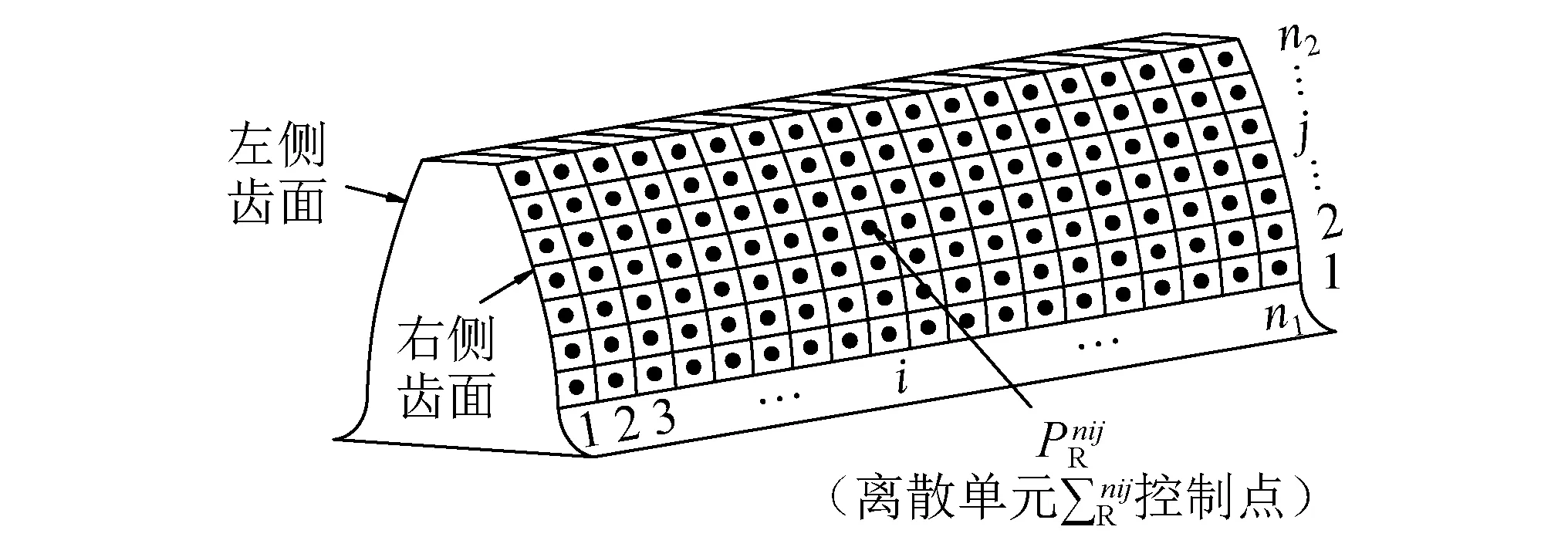
图1 直齿轮离散齿面Fig.1 Discrete tooth surface of spur gear
图2 齿轮加工误差示意图Fig.2 Schematic diagram of gear manufacturing errors
(1)
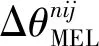
(2)
(3)
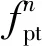
(4)
(5)
(6)
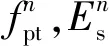
图3为本文中齿轮安装误差的定义。AgBg和ApBp分别是从动轮和主动轮不考虑安装误差时的理论轴线位置。为了简化模型,本文中从动轮和主动轮的安装误差被等效转换到从动轮的轴线上。Ag2Bg2是考虑安装误差后从动轮新的轴线位置。安装误差通过四个参数表示,即Δx,Δy,φ和γ。不同的安装误差可通过上述四个参数的不同组合获得。a是标准中心距。考虑安装误差后,第n个轮齿误差齿面上离散单元控制点的坐标可通过式(7)计算得到

图3 安装误差示意图Fig.3 Schematic diagram of assembly errors
(7)
式中:M13=(1-sinγ)tanφ-sinφ;M23=-sinγ/cosφ;M33=sinγ-cosφ-1;M14=Δx+B[sinφ-(1-sinγ)tanφ];M24=a+Δy+Bsinγ/cosφ;M34=B(cosφ+1-sinγ)。
2 齿轮承载接触分析
传统的齿轮承载接触分析算法计算过程复杂且存在数值不稳定等缺点[18]。图4展示了本文所建立误差齿面模型中的部分齿面。由图4可知,该误差齿面由多个大小相等的离散单元组成,且由于加工、安装误差的影响,各离散单元与理论齿面之间的距离不等。此外,为考虑由齿轮加工、安装误差导致的轮齿脱啮、线外接触等一系列非正常啮合现象对时变啮合刚度和综合啮合误差的影响,本文提出通过检测齿面干涉状态来判定轮齿是否参与接触,其又可转化为通过检测误差齿面上离散单元的干涉状态来判定轮齿是否参与接触。
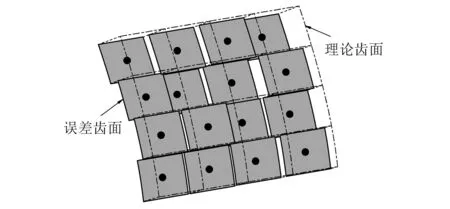
图4 误差齿面示意图Fig.4 Schematic diagram of error tooth surface
齿轮承载接触分析通过一个迭代过程完成,如图5所示。当齿轮误差齿面模型建立后,对于从动轮的每一个输出位置,将以一定步长旋转主动轮,每次迭代过程中判定轮齿是否接触并计算齿轮副所产生的力矩,根据计算结果结合二分法调节主动轮旋转步长,直至齿轮副所产生力矩与负载平衡,最终输出从动轮各位置处的时变啮合刚度和综合啮合误差。
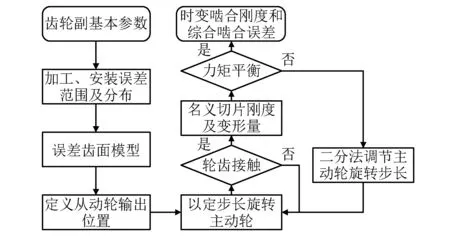
图5 承载接触分析流程图Fig.5 Flow chart of load tooth contact analysis
切片法已广泛应用于斜齿轮副时变啮合刚度的研究中[19-21]。传统切片法将齿轮沿齿宽方向划分为多个切片,而每个切片之间是相互独立的,即忽略切片之间的相互影响[22]。当齿轮为不考虑误差的理想齿面时,该方法能取得较为准确的计算结果。然而,当考虑齿轮加工、安装误差时,齿面上会出现瞬时接触线不连续、偏载等非正常啮合现象,传统切片法将导致较大的计算误差。因此,本文引入名义切片的概念。如图1所示,本文中误差齿面也可看作由n1个切片组成,而每个切片又由n2个离散单元组成。齿轮传动过程中,轮齿在载荷作用下会产生受载变形,而轮齿变形可被分为全局变形,包括轮齿弯曲、剪切、轴向压缩以及齿轮基础变形;局部变形,即赫兹接触变形[23]。如图6(a)所示,初始位置下,由于齿轮加工、安装误差的影响,各切片之间存在间隙和随着主动轮的转动,各切片之间的间隙减小且部分切片参与接触,但由于齿轮副产生的力矩不足以与负载平衡,主动轮将继续转动,直至齿轮副所产生力矩与负载平衡,假设力矩平衡时,各切片接触状态如图6(b)所示。假设失去接触的切片与相邻接触切片具有相同的全局变形,并且这些切片共同构建了一个新的名义切片在每个名义切片上,具有最大变形量的切片被视为该名义切片的接触中心。
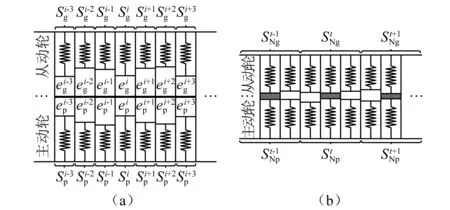
图6 直齿轮副接触过程Fig.6 Contact process of spur gear pair
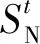
(8)

(9)
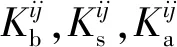
根据Yang等[25],大齿轮和小齿轮之间的赫兹接触刚度可由式(10)计算
(10)
式中,E为齿轮材料弹性模量。
图6(b)中各切片由多个离散单元组成,为通过式(8)计算各名义切片的啮合刚度,还需确定各切片上参与啮合单元的位置。前文中将各离散单元等效为具有不同曲率半径的圆柱面,因此,两齿轮齿面上任意两个离散单元(Σngigjg和Σnpipjp)存在四种接触状态,如图7所示。当不考虑安装误差时,两离散单元(Σngigjg和Σnpipjp)的圆柱轴线平行,如图7(a)和图7(b)所示。基于空间直线方程,并结合离散单元控制点坐标和法向量可求得两圆柱轴线之间的距离dc,则切片总变形为
(11)
式中,ρngigjg和ρnpipjp分别为离散单元Σngigjg和Σnpipjp对应的曲率半径。
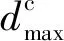
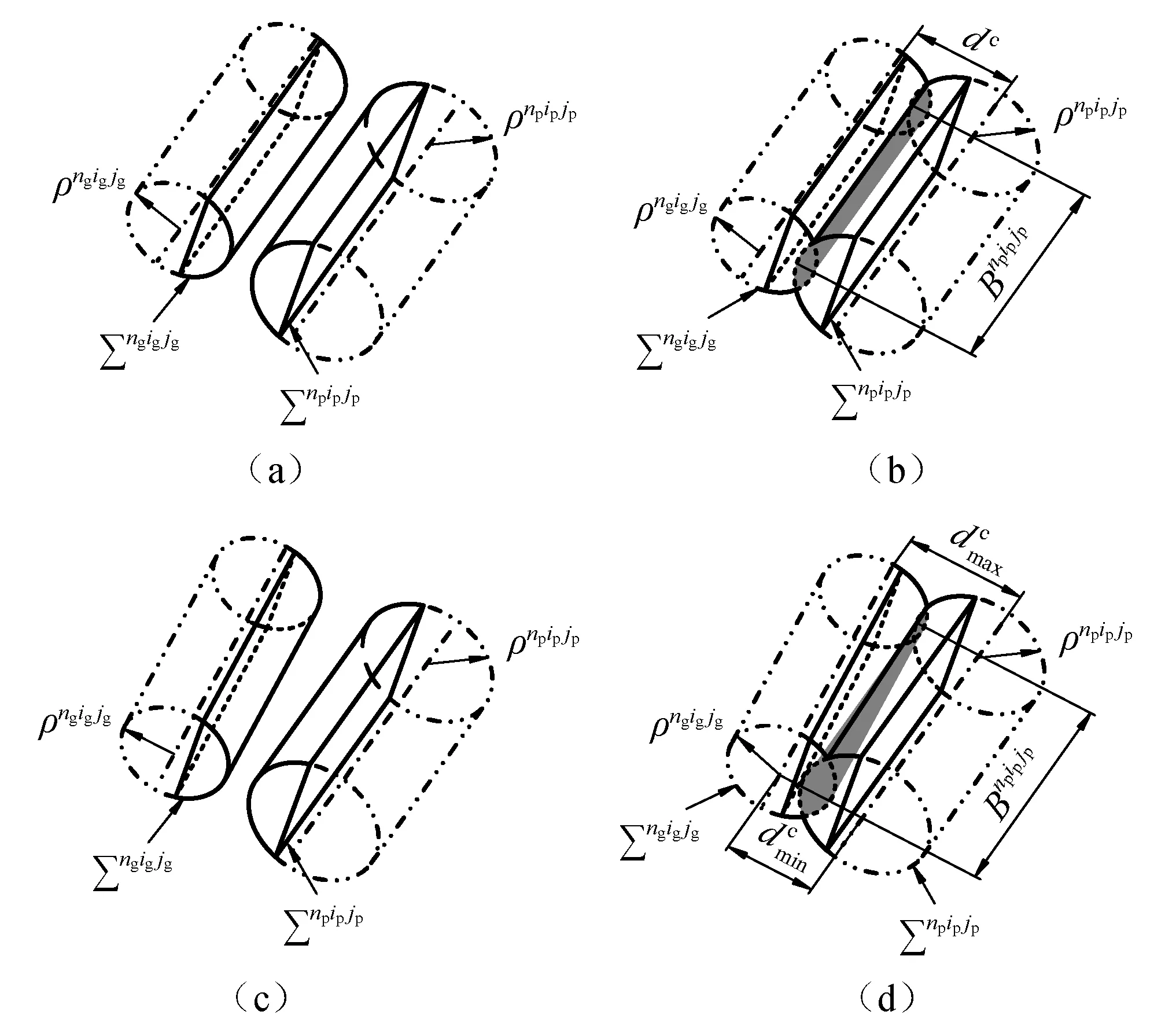
图7 离散单元接触状态Fig.7 Contact state of two discrete elements
(12)
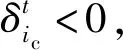
齿轮副力矩平衡方程为
(13)
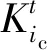
齿轮副的时变啮合刚度可通过所有名义切片的刚度求和而得
(14)
假设空载下主从动轮初始接触时,从动轮的输出位置为θg,而主动轮的转动角度为θp,则综合啮合误差为
e=(θg-θpzp/zg)rbg
(15)
式中,zg和zp分别为从动轮和主动轮齿数。
3 动力学建模
不考虑齿面摩擦的影响,建立如图8所示直齿轮副弯扭耦合动力学模型。根据牛顿第二定律,可推得系统的动力学分析模型为
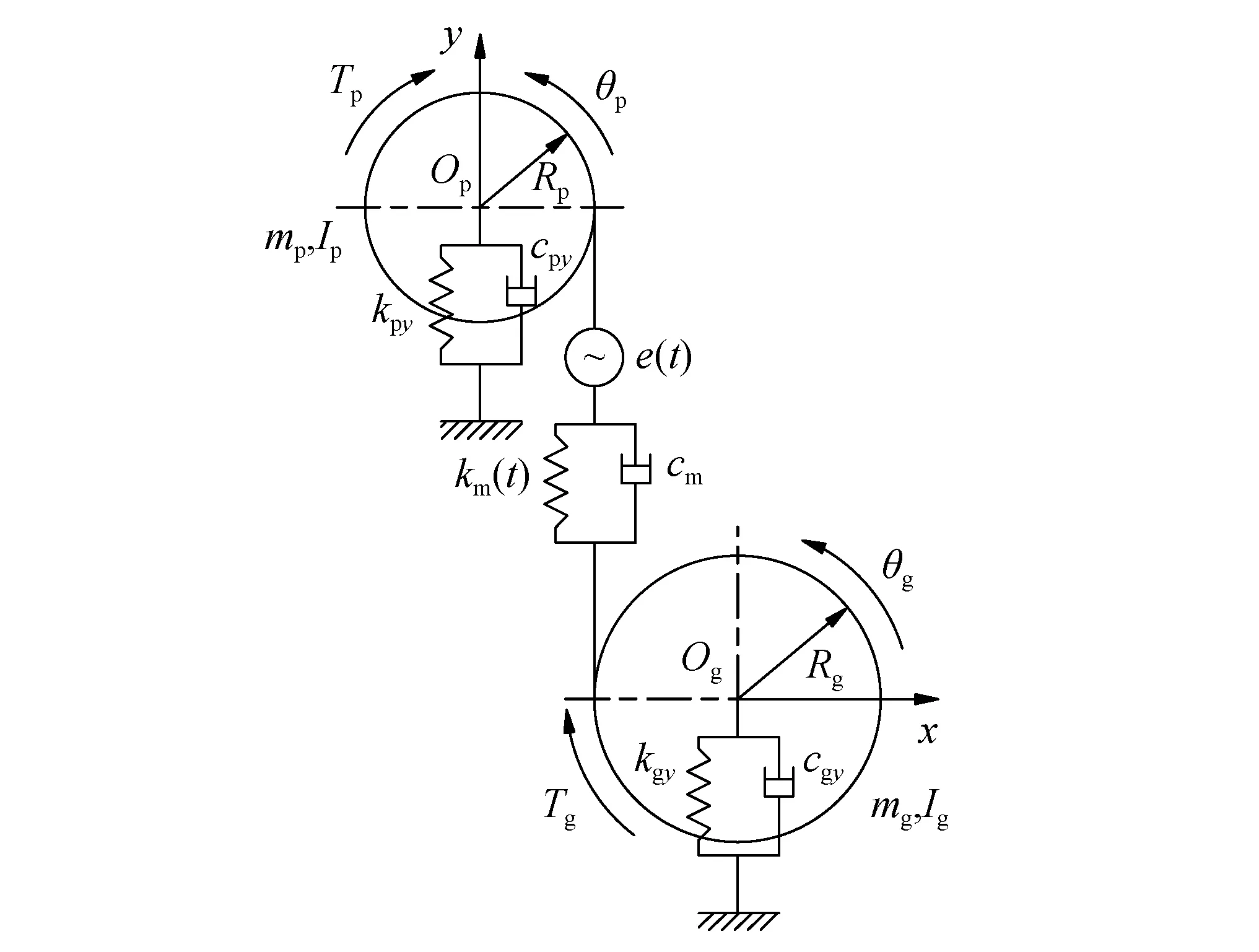
图8 齿轮系统动力学模型Fig.8 Gear system dynamic model
(16)
式中,下标p和g分别为主动轮和从动轮;m和I分别为齿轮的质量和转动惯量;ky和cy分别为齿轮沿y方向的支撑刚度和阻尼;y和θ分别为齿轮在y方向和扭转方向的振动位移;rb为齿轮的基圆半径;T为齿轮的扭矩;cm和km(t)分别为啮合阻尼和时变啮合刚度;δ为沿啮合线的动态传递误差,δ可表示为
δ=-yp-rbpθp+yg-rbgθg-e(t)
(17)
式中,e(t)为时变综合啮合误差。
动力学方程中时变啮合刚度和时变综合啮合误差可分别通过式(14)和式(15)求得。本文中忽略啮合阻尼的时变性,啮合阻尼通过经验公式求得,计算公式为[26]
(18)
式中:ξ为轮齿啮合阻尼比,一般为0.03~0.17,本文取0.1;km为时变啮合刚度均值。
4 计算结果分析与讨论
4.1 模型验证
为了验证本文中齿面离散模型及承载接触分析算法的计算精度,以Chen等研究中的齿轮副为对象,计算理论齿面下的时变啮合刚度和综合啮合误差。本文与Chen等研究中时变啮合刚度计算结果对比如图9所示。通过对比可知,时变啮合刚度均值和峰峰值分别相差2.05%和0.90%,且时变啮合刚度随接触齿对数目的变化而发生突变。此外,理论齿面下,整个啮合周期内齿轮副综合啮合误差为0。上述结果验证了本文中齿面离散模型以及承载接触分析算法的可行性,并说明该方法具有较高的计算精度。
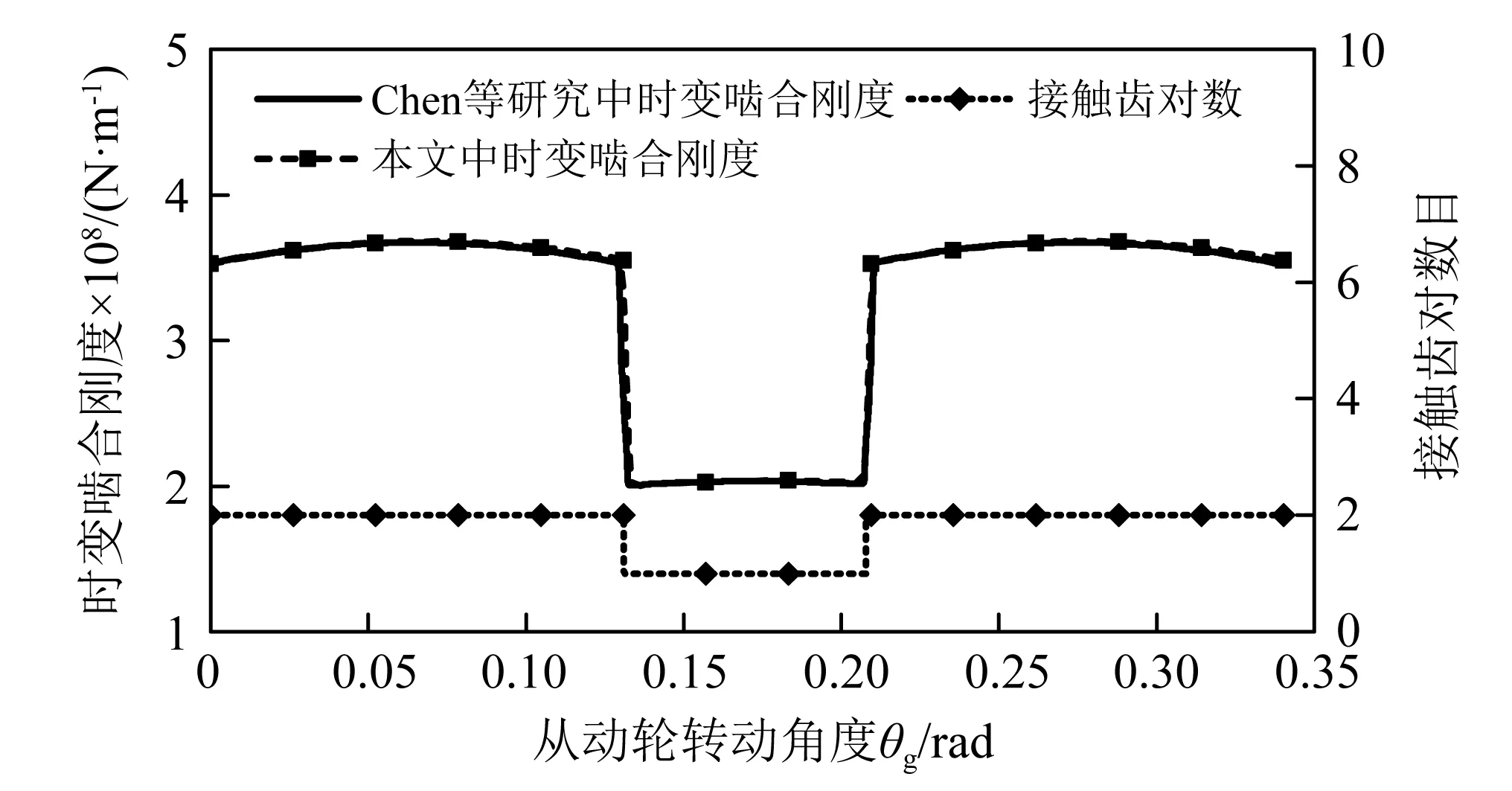
图9 时变啮合刚度和接触齿对数Fig.9 Time-varying meshing stiffness and number of contact tooth pairs
4.2 加工误差对内部激励影响分析
齿轮副时变啮合刚度和综合啮合误差的计算结果不仅受到加工和安装误差的影响,还会受到轮齿啮合次序的影响。当主从动齿轮齿数不同时,主动轮旋转一周后,相互啮合的轮齿发生变化,从而影响时变啮合刚度和综合啮合误差的计算结果。为了避免计算周期过长,本文中选用具有相同齿数的主从动轮作为研究对象,齿轮副参数如表1所示。
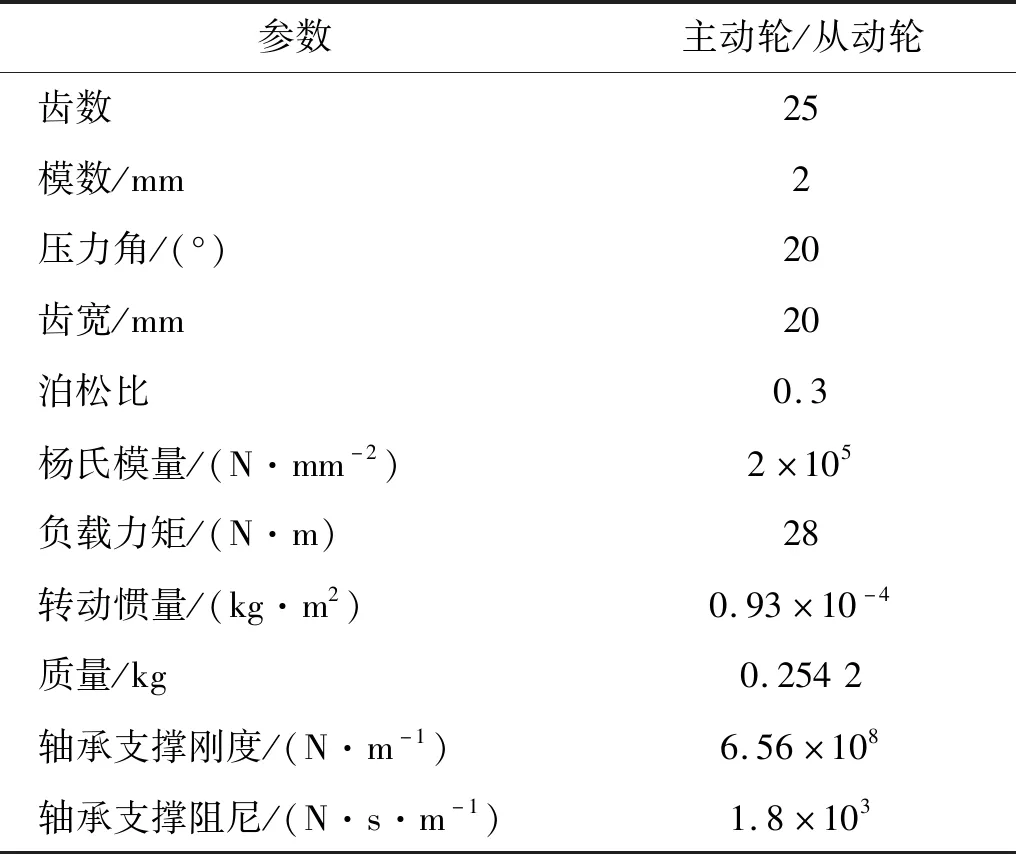
表1 直齿轮副参数Tab.1 Parameters of spur gear pair
本文中主从动齿轮均采用5级精度,根据ISO齿轮精度标准,齿轮副精度参数如表2所示。

表2 直齿轮副精度参数Tab.2 Precision parameters of spur gear pair
齿距累积偏差通常在多个轮齿上大致呈正弦形式分布,多数文献中使用正弦函数来模拟齿距累积偏差,但忽略了齿距累积偏差的随机性。参照袁冰等研究中齿距累积偏差生成模式,本文中采用正弦函数与服从正态分布的随机变量叠加来模拟齿距累积偏差。主动轮和从动轮的齿距累积偏差如图10所示。另外,齿面各离散单元齿廓偏差幅值和各轮齿齿厚偏差幅值均通过随机函数在其公差带中选取。当齿轮生成完成后,校核其公法线长度,若不满足要求,则上述偏差重新选取,直至齿轮副所有精度参数满足表2中所示公差范围。
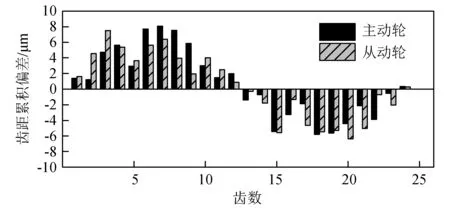
图10 齿距累积偏差Fig.10 Cumulative pitch deviation
不同类型加工误差影响下直齿轮副时变啮合刚度和综合啮合误差,如图11所示。由图11可知,理论齿面下时变啮合刚度呈周期性变化,且综合啮合误差为0。当考虑齿距偏差时,时变啮合刚度在θ1= 0.932 0 rad和θ=2.265 4 rad处发生突变,且在θ1区间[0.932 0,1.017 5]和[2.122 3,2.265 4]中时变啮合刚度大幅减小。此外,当考虑齿距偏差时,综合啮合误差发生阶跃变化,这说明由于齿距偏差的影响,在啮合齿面间产生了不同的初始间隙。为研究时变啮合刚度产生突变及大幅减小的原因,计算了从动轮不同转角下接触齿对数目,如图12(a)所示。在θ1区间[0.932 0,1.017 5]和[2.122 3,2.265 4]中,由于齿距偏差的影响,接触齿对数目由双齿接触变为单齿接触,从而导致时变啮合刚度大幅减小,甚至发生突变。同时,结合图11(b)中综合啮合误差分析可知,综合啮合误差阶跃值最大为5.580 8 μm,其次为4.669 7 μm,它们分别对应区间[2.122 3,2.265 4]和[0.932 0,1.017 5]与相邻区间综合啮合误差的差值。由此说明,齿距偏差导致啮合齿面间产生初始间隙,而该间隙无法被轮齿受载变形补偿时,将导致部分齿对脱啮,也即当齿轮综合啮合误差阶跃值超过一定范围后会导致时变啮合刚度发生突变。
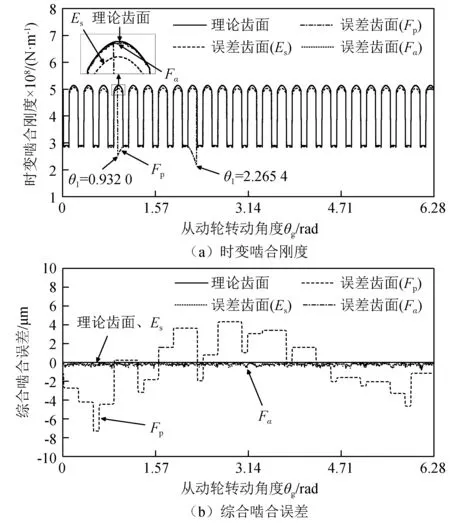
图11 不同加工误差下时变啮合刚度和综合啮合误差Fig.11 Time-varying meshing stiffness and composite meshing error considering different types of manufacturing errors
由图11(a)可知,当考虑齿厚偏差时,时变啮合刚度略微减小,且各啮合周期中时变啮合刚度减小值不同。图12(b)为齿厚偏差影响下从动轮旋转1.570 8 rad时主动轮齿面瞬时接触线,虽然瞬时接触线与理论接触迹重合,但是考虑齿厚偏差会使轮齿减薄,单齿柔度增加,从而使时变啮合刚度略微减小。此外,由图11(b)可知,当考虑齿厚偏差时,综合啮合误差为0。这是由于本文中齿厚偏差通过轮齿的右侧齿面定义,齿距偏差通过左侧齿面定义,如图2所示,而本研究中左侧齿面为工作齿面,因此齿厚偏差的引入并不影响齿轮副的综合啮合误差。
当考虑齿廓偏差时,时变啮合刚度和综合啮合误差在其理论值附近产生微小波动。图12(c)为齿廓偏差影响下从动轮旋转1.570 8 rad时主动轮齿面瞬时接触线。由图可知,受齿廓偏差的影响,主动轮齿面接触线不再与理论接触迹重合,而是分布在其两侧,即发生了线外接触,这是时变啮合刚度和综合啮合误差产生微小波动的原因。

图12 不同加工误差下齿面瞬时接触状态Fig.12 Instantaneous contact state of tooth surface considering different types of manufacturing errors
由上述分析可知,齿距偏差是影响时变啮合刚度和综合啮合误差的主要因素。此外,加工误差的引入会同时影响时变啮合刚度和综合啮合误差,二者深度耦合。在动力学分析过程中,仅通过简谐函数模拟综合啮合误差,而忽略加工误差对时变啮合刚度的影响,难以得到较为精确的动力学分析结果。
4.3 安装误差对内部激励影响分析
根据图3中对安装误差的定义,安装误差由四个参数(Δx,Δy,φ和γ)表示,它们可被分为中心距误差(Δx和Δy)和轴线倾斜误差(φ和γ)两类。由于Δx和Δy对齿轮副中心距的变化影响类似,因此本文中仅考虑安装误差Δy,φ和γ对时变啮合刚度和综合啮合误差的影响,安装误差参数如表3所示。

表3 直齿轮副安装误差Tab.3 Assembly errors of spur gear pair
不同安装误差下时变啮合刚度和综合啮合误差,如图13所示。由图13(a)可知,在安装误差Δy的影响下,当中心距增大时,时变啮合刚度减小,且由于中心距增大,啮合齿面间初始间隙增加,从而导致单齿啮合区间变大,而双齿啮合区间变小;当中心距减小时,时变啮合刚度增加,而对单、双齿啮合区间影响较小,甚至出现单齿啮合区间略微变大,这是由于在本文28 N·m载荷和-0.2 mm中心距误差下,时变啮合刚度增加导致轮齿受载变形减小,反而延缓了第二对轮齿进入啮合。此外,在安装误差φ和γ的影响下,时变啮合刚度具有不同程度的减小,而单、双齿啮合区间无明显变化,且针对相同大小的轴线倾斜误差(φ和γ),轴线倾斜误差φ对时变啮合刚度的影响更大。图14为从动轮旋转0.314 2 rad时,主动轮齿面瞬时接触线。由图14(a)和图14(d)可知,由于中心距误差Δy的引入,当中心距增加时,主动轮齿面瞬时接触线向齿顶移动,从而导致时变啮合刚度减小;相反地,当中心距减小时,主动轮齿面接触线向齿根移动,从而使时变啮合刚度增加。由图14(b)、图14(c)、图14(e)和图14(f)可知,在轴线倾斜误差φ和γ的影响下,主动轮齿面发生了不同程度的偏载,齿面实际接触线缩短,从而导致时变啮合刚度减小。当φ=±0.1°时,约50%的齿面脱离接触,而当γ=±0.1°时,约33%的齿面脱离接触,因此相同大小误差下,轴线倾斜误差φ对时变啮合刚度的影响大于轴线倾斜误差γ。
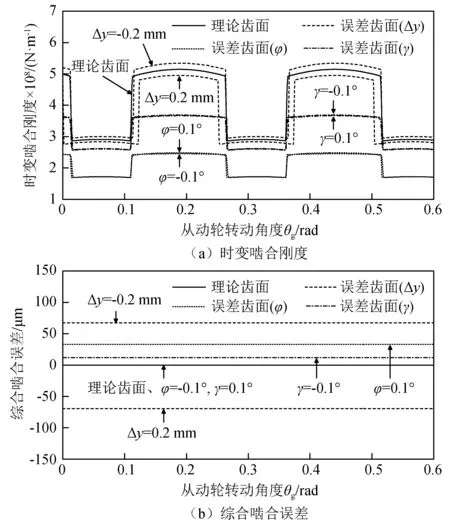
图13 不同安装误差下时变啮合刚度和综合啮合误差Fig.13 Time-varying meshing stiffness and composite meshing error considering different types of assembly errors
由图13(b)可知,在安装误差的影响下,齿轮副综合啮合误差为一定值,且当齿面为理论齿面或轴线倾斜误差φ=-0.1°和γ=0.1°时,综合啮合误差为0。当φ=0.1°和γ=-0.1°时,综合啮合误差分别为32.884 5 μm和11.928 0 μm。当中心距减小时(Δy=-0.2 mm),综合啮合误差为正值,即67.394 3μm;当中心距增大时(Δy=0.2 mm),综合啮合误差为负值,即-69.392 3 μm。
4.4 系统动态特性分析
为研究加工误差和安装误差对系统动态特性的影响,将上文求得的时变啮合刚度和综合啮合误差代入动力学方程,并在MATLAB软件中利用ODE15S进行仿真,计算了不同误差下齿轮副的动态传递误差,并对计算结果在时域和频域内进行分析。
理论齿面下和所有类型加工误差综合作用下齿轮副动态传递误差及其频谱特性,如图15所示。本研究中主动轮转速为2 400 r/min,啮合频率为fm=0.1×104Hz。由图15可知,理论齿面下动态传递误差峰峰值为4.158 2 μm,其频谱成分主要为啮合频率及其倍频。考虑所有类型加工误差时,动态传递误差峰峰值为7.437 4 μm,其峰峰值较理论齿面明显增大。此外,对比图15(c)和图15(d)可知,考虑所有类型加工误差后,动态传递误差频谱中1×104~2×104Hz间高频成分显著增加,而幅值有所减小。为研究动态传递误差的主要影响因素及频谱中高频成分的来源,分别对不同类型加工误差作用下的动态传递误差进行了分析,如图16所示。
当分别考虑齿距偏差、齿厚偏差和齿廓偏差时,动态传递误差峰峰值分别为8.392 1 μm,4.043 5 μm和5.396 1 μm。与理论齿面下动态传递误差计算结果对比可知,齿距偏差和齿廓偏差均导致动态传递误差峰峰值增加,且齿距偏差的影响大于齿廓偏差,而齿厚偏差对动态传递误差峰峰值的影响较小。虽然当仅考虑齿厚偏差时和理论齿面下,综合啮合误差均为0,但齿厚偏差的引入导致轮齿减薄,时变啮合刚度的变化导致动态传递误差峰峰值减小。相较于齿廓偏差,当考虑齿距偏差时,动态传递误差峰峰值与考虑所有类型加工误差时动态传递误差的峰峰值更为接近。此外,从动态传递误差的频谱分析图可以看出,当仅考虑齿厚偏差时,其频谱成分与理论齿面下相同,均为啮合频率及其倍频,而当考虑齿距偏差和齿廓偏差时,动态传递误差频谱中1×104~2×104Hz间高频成分均有增加,其中齿距偏差下动态传递误差高频成分增加更为显著,且与考虑所有类型加工误差时的频谱成分更为接近。因此,齿距偏差是影响动态传递误差的主要因素,且齿距偏差是动态传递误差频谱中高频成分的主要来源。为减小齿轮系统动态传递误差的峰峰值,齿距偏差应根据载荷大小合理分配,避免由于轮齿脱啮导致的时变啮合刚度突变对动态传递误差的影响。
图17为不同安装误差下动态传递误差计算结果。根据前文中时变啮合刚度和综合啮合误差计算结果可知,理论齿面下和轴线倾斜误差φ=-0.1°以及γ=0.1°时,综合啮合误差均为0,通过对比图15(a)、图17(c)和图17(e)可见,时变啮合刚度均值越小,动态传递误差均值越大。此外,图17(a)~图17(f)中,动态传递误差的峰峰值分别为6.002 8 μm,4.675 9 μm,2.899 4 μm,4.717 0 μm,5.033 0 μm和2.882 0 μm。由图13和图14可知,当γ=0.1°时,约33%的齿面脱离接触,时变啮合刚度均值和峰峰值减小,从而导致动态传递误差的峰峰值减小;然而,当φ=-0.1°时,约50%齿面脱离接触,时变啮合刚度的均值和峰峰值进一步减小,反而使动态传递误差的峰峰值增加。对中心距误差而言,当Δy为负偏差时,时变啮合刚度均值增加;当Δy为正偏差时,时变啮合刚度均值减小;同样大小的中心距误差下,负偏差对动态传递误差峰峰值的影响小于正偏差。由图13(b)可知,在安装误差影响下,齿轮副综合啮合误差为一定值。对比图17(b)和图17(e)可知,当时变啮合刚度相同时,综合啮合误差的均值对动态传递误差的均值和峰峰值影响较小。此外,从动态传递误差的频谱分析中可以看出,不同类型安装误差下,其频谱成分主要为啮合频率及其倍频。
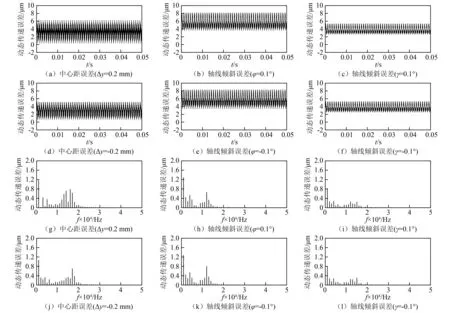
图17 不同类型安装误差对动态传递误差的影响Fig.17 Influence of different types of assembly errors on dynamic transmission error
综上分析可知,为减小动态传递误差的峰峰值,应避免由轴线倾斜误差引起的偏载现象发生,虽然一定程度内的偏载导致时变啮合刚度均值和峰峰值减小,使动态传递误差峰峰值减小,但超过一定范围后,不仅动态传递误差的峰峰值增加,也会导致齿面接触应力增加,缩短齿轮疲劳寿命。此外,虽然本文中中心距负偏差对动态传递误差峰峰值的影响小于正偏差,但是中心距负偏差会进一步导致啮入冲击激励增大,不利于改善高速齿轮系统的动态性能。
5 结 论
(1)加工、安装误差同时影响时变啮合刚度和综合啮合误差,二者深度耦合。加工误差中,齿距偏差是时变啮合刚度和综合啮合误差的主要影响因素;齿距偏差作用下,综合啮合误差呈阶跃变化,当阶跃值超过一定范围后会导致轮齿脱啮,时变啮合刚度发生突变;齿距偏差也是齿轮系统动态传递误差的主要影响因素。
(2)安装误差影响下,综合啮合误差在整个啮合周期内为一定值;中心距误差导致瞬时接触线在齿面上移动,时变啮合刚度随中心距的增加而减小;轴线倾斜误差导致齿轮出现偏载现象,齿面接触线缩短,时变啮合刚度减小,且轴线倾斜误差φ较轴线倾斜误差γ对时变啮合刚度的影响更大。
(3)为减小齿轮系统动态传递误差的峰峰值,齿距偏差应根据载荷大小合理分配,同时应避免由轴线倾斜误差引起的偏载现象发生;此外,虽然中心距负偏差对动态传递误差峰峰值的影响小于正偏差,但在采用中心距负偏差时,应结合齿廓修形,降低由中心距负偏差带来的啮入冲击。

