L型管路系统动力学有限元建模及基于遗传算法的卡箍支撑位置优化
高志辉,王东海,孙 伟,汪 博
(1.东北大学 机械工程与自动化学院,沈阳 110819;2.东北大学 航空动力装备振动及控制教育部重点实验室,沈阳 110819)
航空发动机管路系统结构复杂,主要用于完成燃油、滑油、空气等介质的输送。由于内部空间有限,给管路系统安装、约束、维护带来很多限制,导致纯直管管路较少,更多的是L型、Z型或者更为复杂的空间异面管路。本文以L型管路为对象开展相关研究。
航空发动机管路在工作过程中会受到转子、传动组件和泵源压力脉动的激励而产生振动,过大的振动可能会导致卡箍松动、接头裂纹等故障[1],因而需要研究有效减少管路系统过大振动的方法。管路中卡箍的力学特性(主要是支撑刚度及阻尼)直接影响管路系统的动力学特性,因而在设计阶段通过调整卡箍布局使其有效避开发动机转子的激振频率通常被认为是一种最简单、最经济的减振方法[2]。
为了完成以避振为目标的管路系统支撑位置优化,首先要研究创建管路系统的动力学模型作为优化研究的基础模型。当前对管路系统动力学建模的众多方法中,有限元法是一种最重要的方法,典型研究诸如Wu等[3]推导出了一种水平曲梁单元,将其用于有一定弧度的弯曲结构自由振动分析。Fonseca等[4]提出位移场由一组三角函数或五阶多项式定义的有限弯曲壳单元,来解决受面内弯曲力作用的弯管应力分析问题。Zhai等[5]选用Timoshenko梁单元,推导出输流管道的刚度矩阵及质量矩阵,建立了动力学有限元方程并执行了随机激励下管路系统动态响应计算。Gao等[6]基于Euler-Bernoulli梁理论,采用有限元方法建立了输流管道的运动方程,通过引入人工弹簧来模拟任意边界条件,提出了一种基于模态综合的管道模型降阶的有效求解方法。上述针对管路有限元建模的理论研究,所针对的对象或者是圆弧形弯管或者是直管,并未考虑直管与弯管部分的结合,因而相关有限元理论并不适用于同时含有弯管及直管的L型管路的建模。
当前,以减振为目标的管路卡箍位置优化已开展了部分研究。例如Zhang等[7]通过非概率灵敏度分析,研究了航空液压管路系统中卡箍的设计问题,针对不同位置的卡箍,筛选出对最大应力响应、最大位移响应和一阶固有频率不敏感的个体,进一步执行了卡箍布局优化以提升管路系统的抗振性。李鑫等[8]通过优化飞机液压系统的卡箍布局方式,降低了系统激振源频率点的特征阻抗加权和。权凌霄等[9]采用ANSYS软件平台中的灵敏度分析工具,分析航空液压管路支架参数对振动响应的灵敏度,在此基础上,采用多目标遗传算法对管路支架布局进行优化设计。Tang等[10]以卡箍位置为设计变量,以累积疲劳损伤失效概率为优化目标,建立了减振优化模型并执行了卡箍布局优化。陈艳秋等[11]利用NSTRAN软件分析了航空管路系统的动力学特性,并用遗传算法对管路系统分别进行调频和调幅的卡箍布局优化。翟红波等[12]综合考虑了管路系统优化设计变量,通过优化卡箍位置、刚度和管径提高了系统的首超可靠性。Zhang等[13]分析了多卡箍支撑的管路系统,得到了卡箍位置的灵敏度,以避振和减小应力为目标用多目标遗传算法进行优化设计。刘伟等[14]分析了结构参数对管路系统基频和随机振动的灵敏度,在此基础上,分别以基频与激振频率差值最大化及随机振动响应均方差最小化为目标,对卡箍位置进行优化设计。上述关于卡箍布局优化研究多集中于使用工程有限元分析软件,划分网格时会降低计算效率,且主要针对的是航空或者输油气管路。目前以航空发动机管路为对象或者背景以避振为目标的卡箍布局优化研究还不充分。
另外,由于航空发动机空间限制,卡箍有时不一定能处于优化结果对应的最优位置,但其处于一定范围时,也可满足避振需要。因而,在管路设计中,对于一个特定的卡箍存在一个满足避振要求的容许移动范围,这里命名为“安全域”。以作者的认知,目前还没有对这个“安全域”开展充分的研究。
本文以L型管路为研究对象,研究管路系统动力学有限元建模及基于遗传算法以避振为目标的卡箍支撑位置优化方法。具体包括:提出了“以直代曲”的L型管路有限元建模方法;创建了以避振为目标的卡箍布局优化模型以及描述了基于遗传算法求解该优化模型的方法;进行了实例研究,在用试验校验有限元模型合理性的基础上,用所提出的优化方法确定了卡箍最优的布局,尤其是分析确定了各卡箍满足避振条件下的可移动范围,即“安全域”。
1 L型管路动力学有限元建模
1.1 “以直代曲”管体有限元建模原理
在现有的研究中,对于管路动力学模型的建立一般采用梁单元,对于图1所示的L型管路,这里用三维Timoshenko梁单元进行模拟。
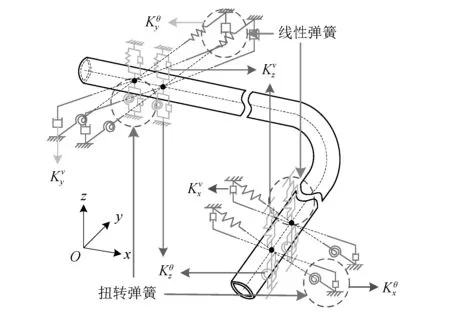
图1 L型卡箍-管路动力学模型Fig.1 Dynamic model of L-type hoops-pipe system
如图2所示,所选的梁单元共有2个节点,每个节点有6个自由度,分别为沿x,y,z轴的线性自由度及对应扭转自由度。这样,单元的自由度可以表示为
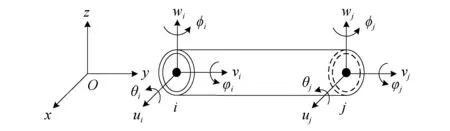
图2 Timoshenko梁单元Fig.2 Timoshenko beam element
qe=[uiviwiθiφiφiujvjwjθjφjφj]T
(1)
针对L型管路动力学有限元建模,重点在于描述清楚弯管部分的建模方法,这里用“以直代曲”的方法模拟弯曲段。如图3所示,将弯管段近似划分为微小的直管,进而即可用直梁单元进行建模,然后用多个梁段模拟弯管的力学行为。图中:D为管路外径;R为管路弯曲半径;l=R×π/2(n-1)为弯曲段以直代曲建模时直梁单元长度;n为弯曲段划分单元数。为保证计算效率及结果准确性,弯曲段划分单元长度应与直管段单元长度相近,从而使整体结构单元划分均匀协调。1,2,…,i,i+1,…,m-1,m为弯曲段梁单元各个节点,在数值上,n=m-1,O为弯曲中心,虚线部分表示省略部分单元。
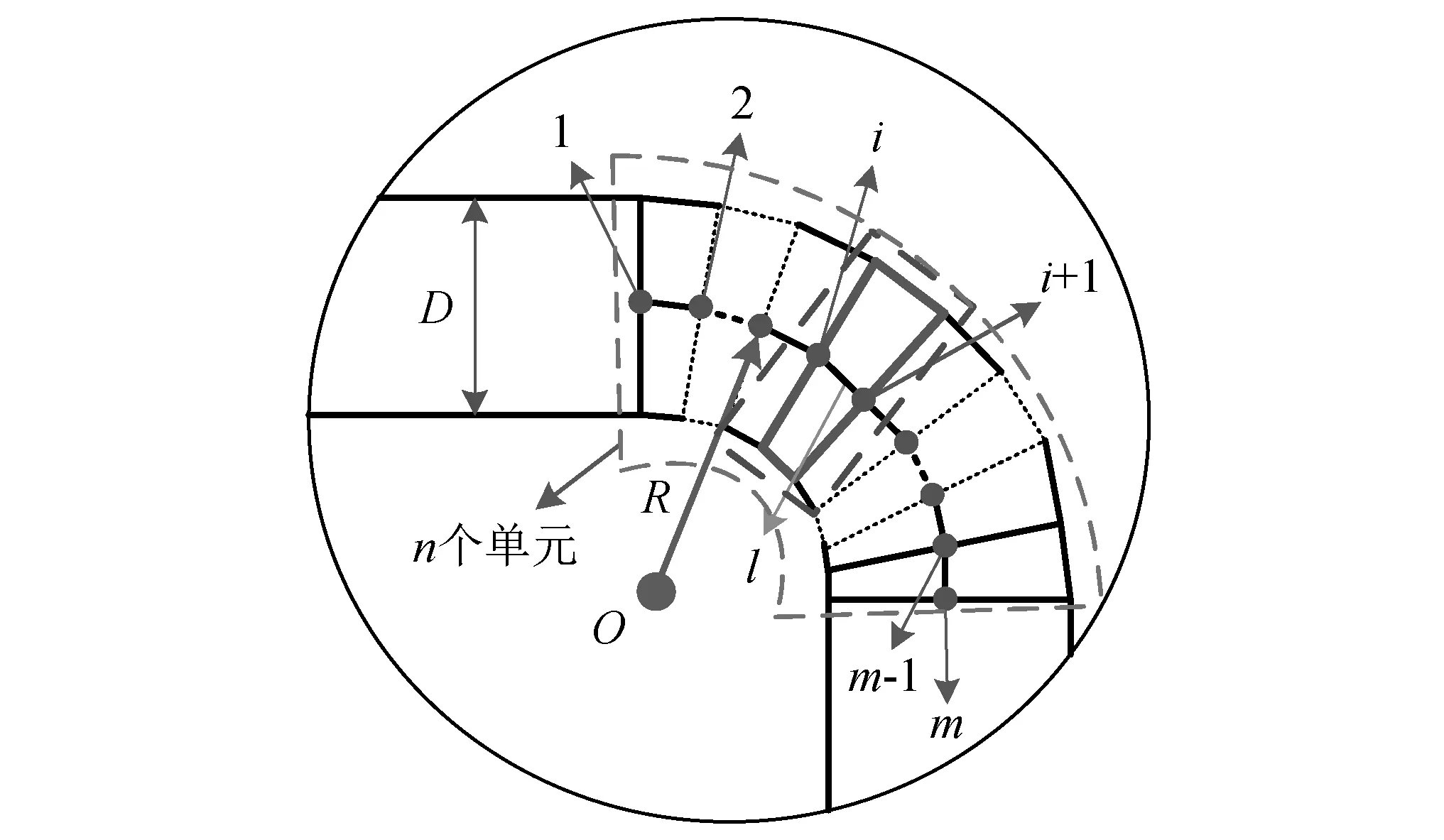
图3 L型管路弯曲段俯视局部放大图Fig.3 The top view partial enlarged drawing of L-type pipe bending section
划分完单元后,求出弯曲段直梁单元在各自局部坐标系下的刚度矩阵和质量矩阵,而后,需要进行单元刚度矩阵、质量矩阵的组集。在组集过程中,需要对单元刚度矩阵和质量矩阵进行局部坐标系和整体坐标系的转换,下面以弯曲段第k个单元为例,介绍转换过程。
如图4所示,O-xyz为整体坐标系,O′-x′y′z′为弯曲段第k个单元局部坐标系。考虑到单元的局部坐标系和总体坐标系的关系,局部坐标系中第k个直梁单元各节点位移在总体坐标系下可表达为

图4 L型管路弯曲段第k个单元示意图Fig.4 The schematic diagram of the k-th element of L-type pipe bending section
(2)
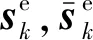
L=diag(T,T,T,T)
(3)
其中,
(4)
进一步,这里
(5)
式中,λk为第k个单元处总体坐标系x轴与局部坐标系x′轴的夹角;为避免单元和节点表示方法产生混淆,xi,xi+1,yi,yi+1分别为第i个和第i+1个节点在整体坐标系中坐标值,在数值上,k=i,则“以直代曲”的梁单元在总体坐系中的单元刚度矩阵和质量矩阵为
(6)
(7)
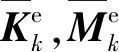
1.2 卡箍的模拟
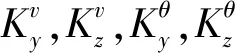
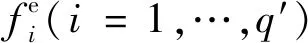
(8)
迭代结束后,即可获得满足精度要求的弹簧对的4个刚度值参数。
1.3 运动方程建立以及固有特性求解
以下具体描述模拟卡箍的弹簧单元引入管路系统动力学分析模型的方法,并由此建立用于求解管路系统固有特性的运动方程。
创建一个与管体有限元模型自由度相等的零矩阵,接着找到模拟卡箍的弹簧单元对应的节点,将弹簧单元的刚度值加到零矩阵的对角线上,形成卡箍刚度矩阵Kk,具体为
(9)
其中,
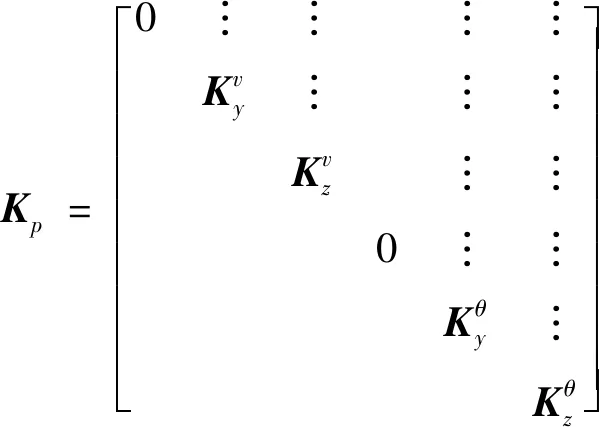
(10)

(11)
式中:p为L型管路长边添加弹簧单元节点号;q为短边添加弹簧单元节点号。
将卡箍刚矩阵与管体刚度矩阵进行叠加可得到管路系统的总刚度矩阵K,表达为
K=Kw+Kk
(12)
而管路系统的质量矩阵就为管体的质量矩阵,表达为
M=Mw
(13)
综上,可得到求解管路系统固有特性求解方程为
(14)
其中:ωr和φr分别为管路第r阶固有圆频率及模态振型向量;n′为系统节点数。
2 L型管路卡箍支撑位置优化
为了完成面向L型管路的以避振为目标的卡箍支撑位置优化,需要创建相应的优化模型以及采用有效的寻优算法对该优化模型进行求解,本节具体描述上述问题。
2.1 L型管路避振优化模型
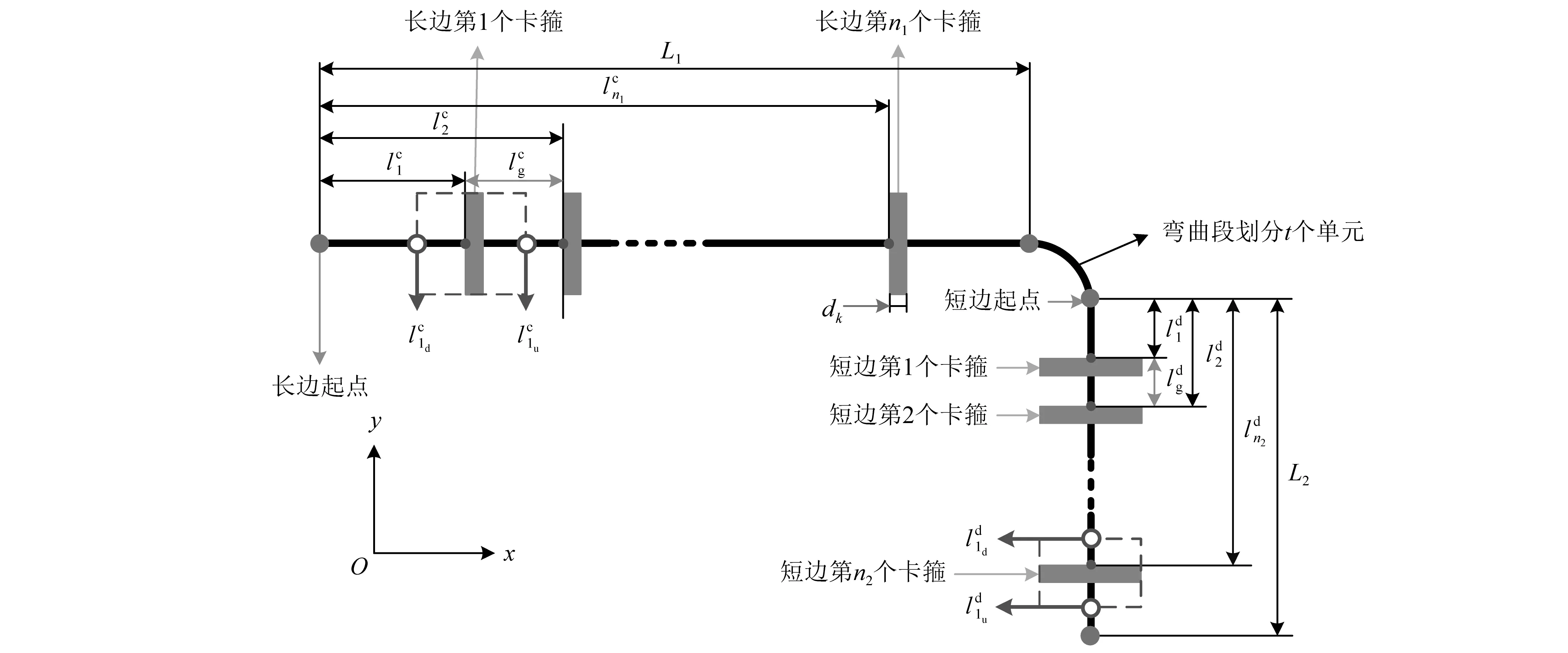
图5 L型管路避振优化模型俯视图Fig.5 Top view of optimization model of L-type pipeline vibration avoidance
(15)
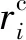
为保证航空发动机安全性,在现有的管路系统设计准则中,要求管路系统的固有频率要远离转子的激振频率,即保证系统的固有频率处于安全范围。由于管路系统通常具有较高的刚度,通常情况下要求卡箍-管路系统第1阶固有频率f1需满足f1>1.25SH,其中,SH为转子系统激振频率。因而,可设卡箍-管路系统固有频率与激振频率的差值为目标函数,使二者有较大差值,这样,可以较好地避开激振源,避免管路系统发生共振。进一步需要设置约束条件限制卡箍在长边及短边上的移动范围。最终,确定该多卡箍支撑L型管路的优化模型为
(16)
2.2 基于遗传算法的优化求解
针对L型管路卡箍避振优化模型,这里采用遗传算法[18]对其求解,该算法中所需术语与优化模型对应关系如图6所示,优化基本流程如下:
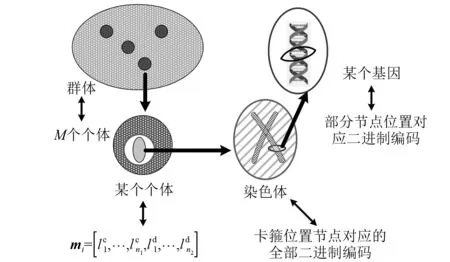
图6 遗传算法与优化模型结合示意图Fig.6 Schematic diagram of the combination of genetic algorithm and optimization model

步骤2个体评价。计算群体P(g′)中各个个体的适应度,即计算各个个体mi(i=1,…,M)中(n1+n2)个卡箍位置对应节点所得出的系统1阶固有频率f1与1.25SH的差值f1SH。
步骤3选择操作。选择每一代中适应度高的个体,对于卡箍-管路优化模型来说,即选择1阶固有频率f1与1.25SH的差值f1SH大的个体。
步骤4交叉变异操作。这里是指交叉及变换各个个体中(n1+n2)个卡箍位置对应节点的二进制编码中的部分片段,从而产生对应新卡箍位置的个体,各新个体组成下一代群体P(g′+1)。
步骤5终止条件判断。若g′=G,则以进化过程中所得到的具有最大适应度,即1阶固有频率f1与1,25SH的差值f1SH最大的个体作为最优解输出,同时输出该个体中(n1+n2)个卡箍位置对应节点号,终止运算;若g′ 这里选取如图7所示L型管路试验系统,来校验研发的有限元模型,并以此为基础实施卡箍布局优化。为使卡箍能在管路直管段任意位置移动,设计如图8所示夹具,导轨通过螺栓固定在振动台上,滑块通过螺栓、垫片及螺母固定在导轨上。长短边导轨长度不同,滑块相同。经测试,长、短边夹具1阶固有频率远大于所考虑的管路系统频率分析范围,从而不会导致夹具与卡箍-管路系统发生耦合振动。 图7 固有特性测试现场图Fig.7 Schematic diagram of field test of inherent characteristics 图8 夹具放大图Fig.8 The enlarged view of the fixture 表1 L型管路几何及材料参数Tab.1 Geometry and material parameters of L-type pipeline 使用锤击法获得卡箍-管路系统的固有频率及模态振型。所用的仪器及用途描述如下:用PCB SN 30272模态力锤进行锤击,用轻质加速度传感器B &K 4517拾取振动信号,用LMSSCADAS进行数据采集与分析,试验结果通过LMS Impact Testing进行处理。 用第1部分描述的“以直代曲”的方法对L型管路进行有限元建模。在同时考虑卡箍宽度及后续执行优化时计算效率的基础上,对该L型管路进行分网,具体如下:在直管段长边划分为300个单元,短边划分为150个单元,单元长度均为2 mm;同时,弯管段划分为10个单元,单元长度也大致为2 mm。综上,系统共划分为460个单元,共有461个节点。3个卡箍的位置 表2 卡箍刚度值Tab.2 The values of hoop stiffness 通过计算获得L型管路的固有频率及模态振型,相关结果如表3、表4及表5所示(为了比对,试验结果也列在上述表中)。从表中可以看出,用所研发的模型计算获得的前5阶固有频率与试验值的最大偏差为3.2%,模态振型基本一致,从而证明了研发的“以直代曲”建模方法的合理性。需要说明的是,这里第1、第4阶模态为竖直面(z向)振型,第4、第5阶模态为水平面(y向)振型,而第2阶模态既包括竖直面(z向)振型,也包括水平面(y向)振型。 表3 实测与仿真固有频率对比Tab.3 Comparison of measured and simulated natural frequencies 表4 实测与仿真系统竖直面(z向)前3阶振型对比Tab.4 Comparison of the first three modes of vertical plane (z direction) between measured and simulated system 表5 实测与仿真系统水平面(y向)前3阶振型对比Tab.5 Comparison of the first three modes of horizontal plane (y direction) between measurement and simulation system 此外,这里最终形成的管路系统整体刚度、质量矩阵维度均为2 766×2 766阶,利用所研发的程序进行固有频率求解时单次计算所需时间为1.094 320 s(所使用设备为Intel(R) Core(TM) i7-8700 CPU),计算效率较高,可以为工程实际应用提供一定借鉴。 最后,为验证弯管部分单元数量对仿真结果的影响,分别对弯管部分划分5个、8个、10个、20个单元,固有频率仿真结果如表6所示。从表中可以看出当弯管段单元划分为10个时,结果已经收敛。 表6 弯管部分划分单元数对收敛性影响分析Tab.6 Analysis of the influence of the number of dividing elements on the convergence of elbow 综上说明,本文提出的“以直代曲”方法对L型管路进行有限元建模是合理的。 这里将转子系统激振频率SH假定为225 Hz,此时,要求管路1阶频率大于1.25SH=281.25 Hz。由表3可知目前实例中的卡箍位置并不满足此要求,因而要执行以避振为目标的卡箍位置优化。 图9 1.25SH与系统1阶固有频率差值迭代过程Fig.9 The iterative process of the difference between 1.25SH and the first natural frequency 为了验证所得优化结果的合理性,如图10所示,选取2组非最优卡箍位置及最优卡箍位置所得结果进行对比,对应的卡箍布局方案列于表7中。 表7 卡箍布局方案Tab.7 The scheme of hoops layout 图10 卡箍布局方案Fig.10 Scheme of hoops layout 最终获得上述卡箍布局方案的1阶固有频率结果,并将试验优化结果与仿真优化结果进行对比。其结果如表8所示。 从表8可以看出,方案1与方案2卡箍布局方案均不满足避振要求,仿真卡箍布局优化结果与实测值误差为-0.3%,从而验证了本文优化结果的合理性。 表8 优化结果验证Tab.8 Validation of optimization results 前面已述,在实际的管路系统设计中由于空间限制,并不一定能使卡箍处于经优化获得的最优位置,但只要在“安全域”范围内则就满足避振要求。这里对实例中的3个卡箍,基于假定的激振频率进行“安全域”分析。 图11 单个卡箍位置变动安全域Fig.11 The safe region of single hoop position 本文针对L型管路,研究了管路系统有限元建模及以避振为目标进行卡箍支撑位置优化的方法,得出以下结论: (1)L型等平面管路的弯曲部分在采用梁单元进行建模时,可以采用“以直代曲”的方法,即将弯管段近似划分为若干微小的直管,进而用直梁单元进行建模。实践表明用这种方式创建的有限元模型可有效模拟实际管路的振动特性,计算与实测管路的前5阶固有频率,最大偏差为3.2%,模态振型基本一致。 (2)对于包含多卡箍支撑的L型管路,可以将卡箍位置作为设计变量,以管路系统固有频率与激振频率的差值为目标函数,并参照相关标准确定卡箍位置的约束范围,从而创建以避振为目标的管路系统优化模型。实践表明该优化模型能与后续的遗传算法有效结合,实现卡箍位置的布局优化。 (3)在实际的管路系统设计中由于空间限制,并不一定能使卡箍处于经优化获得的最优位置。这里提出了“安全域”概念,并基于卡箍位置优化结果,对实例中3个卡箍的安全域进行分析,确定了满足避振要求的各卡箍可移动范围。3 实例研究
3.1 问题描述




3.2 振动特性分析


3.3 卡箍支撑位置优化

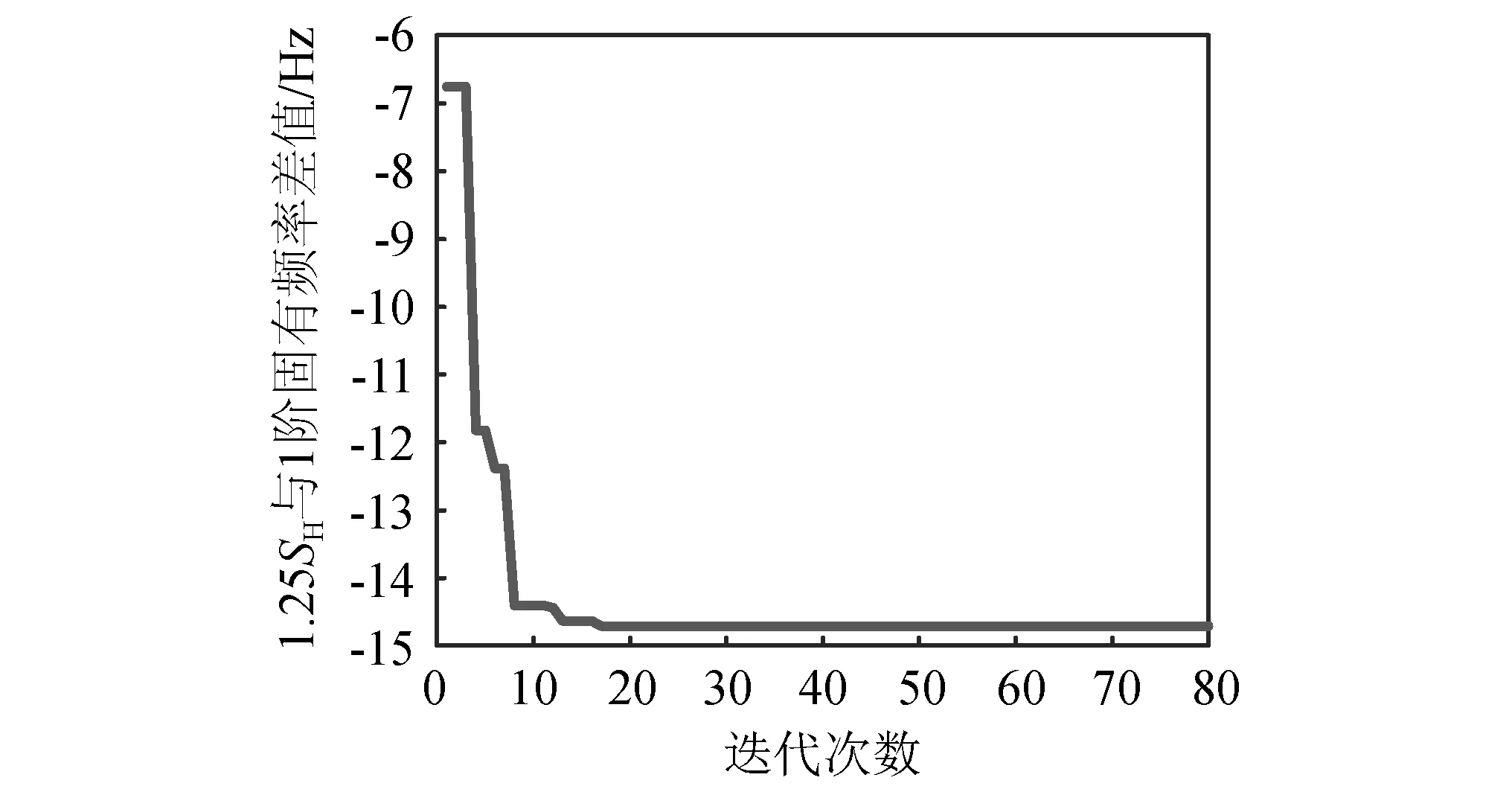



3.4 “安全域”分析
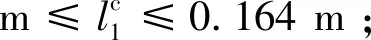
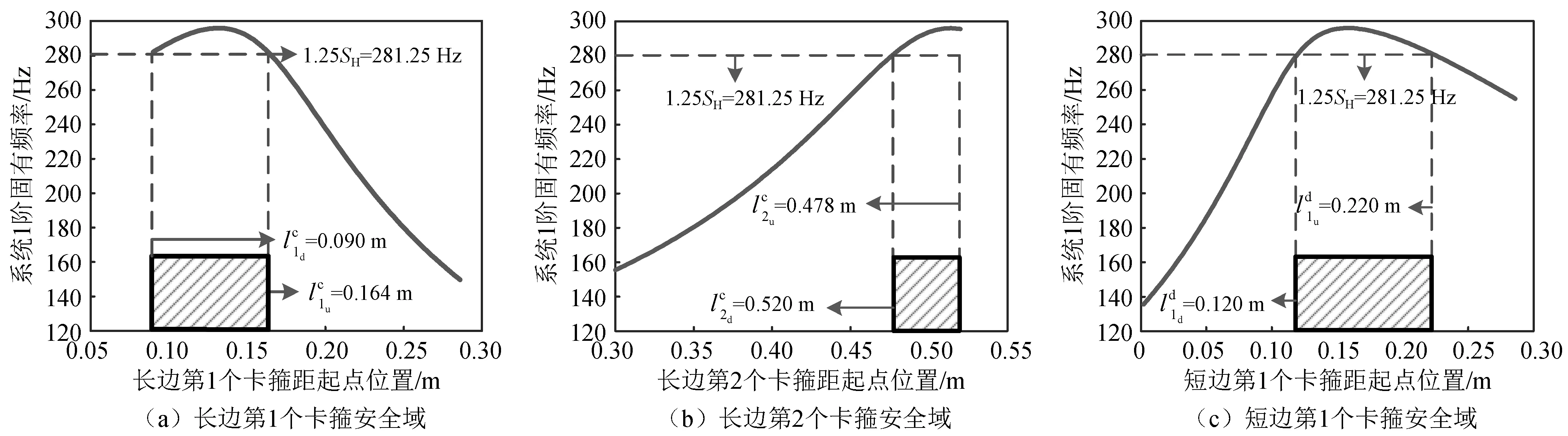
4 结 论

