混合特征驱动的滚动轴承智能故障诊断方法

陆建涛，姚 通，李舜酩，崔荣庆

(南京航空航天大学 能源与动力学院，南京 210016)

滚动轴承广泛应用于大型旋转机械中，如航空发动机、风力发电机、动车组等，是其不可或缺的支撑部件。在旋转机械运行过程中，轴承不可避免发生故障，轻则造成巨大的经济损失，重则机毁人亡造成灾难性事故。若能及时对其进行智能故障诊断，就有望能够保障设备运行安全，避免重大经济损失和事故发生。因此，对滚动轴承进行智能故障诊断具有重要的工程应用价值[1-2]。

振动信号中蕴含着丰富的故障信息，因此基于振动信息的滚动轴承故障诊断一直是研究热点[3]。振动信号常规时域特征指标主要包含两类：一类是有量纲指标，例如最大值、最小值、峰峰值、均值和方差等；另一类是无量纲指标，例如峭度因子，脉冲因子，波形因子等。这些指标在一定程度上反映设备故障特征，如峭度因子反映信号中冲击成分大小，裕度因子反映机械装备的磨损状况，波形因子能反映转子点蚀或者磨损。因此，特征参数的变化可反映出设备运行状态变化情况，可作为对其进行故障诊断的依据。然而，有量纲指标易受外界运行环境和运行工况影响，无量纲指标虽然受外界因素影响较小，但其在故障特征相似程度较高时，识别效果不佳。因此，仅使用常规特征对设备进行故障诊断，诊断准确率较低[4-5]。

超阶分析是在去趋势波动分析法(detrended fluctuation analysis,DFA)基础上提出的用于分析子系统激励源区分度的新方法，利用极值点包含的丰富状态信息，分析极值点背后的因素，有助于解释信号的本质特征[6]。江星星等[7]提出基于超阶分析的排量检测法，提取泵车液压泵体振动信号标度指数，实现泵车的排量标定。超阶分析法既保留了去趋势波动分析法的原有优点，减小序列中趋势成分的影响，又能反映信号的长程相关特性，突出时间序列本来的状态特征，能够揭示信号波动的内在驱动机制。

支持向量机(support vector machine,SVM)是Cortes等[8]提出的基于统计学习理论的机器学习方法，对小样本和非线性问题有较好的表现，目前主要应用于模式识别领域。SVM是从线性可分情况下的最优分类超平面发展而来，首先转化成二次规划问题，然后利用拉格朗日乘子法转化成二次规划的对偶问题来求解。对于线性不可分问题，先把原始数据映射到线性可分的更高维空间，在高维空间构造最优超平面，并映射回原空间，能够较好地解决原空间内线性不可分问题。然而SVM参数的选取较为困难，参数选择不恰当，会造成过拟合或者欠拟合现象，而且核函数中包含的参数对训练和预测的速度有较大影响[9]。

本文针对采用传统特征指标进行故障诊断准确率较低的问题，提出一种基于混合特征指标的滚动轴承智能故障诊断方法。将超阶分析所得标度律指数作为故障特征指标，与常规特征指标相结合构造混合特征指标矩阵，并采用SVM实现滚动轴承的智能故障诊断。为了实现SVM参数的自适应选取，提出基于粒子群优化(particle swarm optimization，PSO)的改进SVM(improved SVM，ISVM)法。最后，通过轴承故障模拟试验台数据对提出方法有效性进行验证。

1 混合特征指标

1.1 常规特征指标

常规有量纲指标容易受到外界工况因素的影响，难以用于实际的故障诊断。无量纲特征指标能够在一定程度上反应设备故障情况，包括：峭度因子、脉冲因子、峰值因子、裕度因子和波形因子等。

(1) 峭度因子

峭度因子是表征振动信号波形尖峰度的一个统计量，具体的含义表示波形的平缓程度，用来描述变量的分布特征[10]。计算公式为

(1)

式中：μ为信号x的均值；σ为信号的标准差；E(t)为t期望值。当轴承发生故障时，振动信号中通常出现周期性的冲击成分，此时峭度因子值大于3，振动信号的整体分布曲线会呈现“陡峭”现象。

(2) 脉冲因子

脉冲因子表征信号振动脉冲的频率，用来检测信号中有无冲击成分的一个指标，其值是振动信号的峰峰值与其整流平均值的比值，计算公式为

I=pk/av

(2)

式中：I为脉冲因子；pk为所监测振动信号的峰峰值；av为所监测振动信号的整流平均值，亦即信号绝对值的平均值。

(3) 峰值因子

峰值因子表征信号峰值在振动信号整体分布波形中的极端程度，跟脉冲因子类似，也是用于检测是否存在冲击成分的一个指标[11]，计算公式为

C=pk/rm

(3)

式中：C为信号的峰值因子；rm为振动信号的有效值(信号的均方根值)。由于振动信号的整流平均值小于有效值，所以脉冲因子大于峰值因子。

(4) 裕度因子

裕度因子是信号的峰峰值与方根幅值的比值，同样对冲击特征比较敏感，但当故障逐渐加重时，其数值反而会下降，表明裕度因子对振动信号中蕴含的早期故障具有较高敏感性，因而常被用来表征机械运行装备磨损状况，计算公式为

L=pk/xr

(4)

式中：L为振动信号的裕度因子；xr为振动信号的方根幅值。

(5) 波形因子

波形因子S是信号有效值与平均幅值之比，可以反映转子出现点蚀或者磨损故障的信号特征，其计算公式为

S=rm/av

(5)

上述5个无量纲特征参数都可以反映设备发生故障时产生的故障特征，但是与信号的频率无关，这也使得在变工况状态下，这5个常规特征参数仍能够表征故障信息。

1.2 超阶分析

对振动信号进行超阶分析过程如下：

(1) 对原始时间序列取极值

(6)

式中，xn≤xn+1，xn+1≥xn+2或xn≥xn+1，xn+1≤xn+2。

(2) 将极值序列变换为极值增量序列

(7)

(3) 对于序列Δxm，计算其累积离差y(t)

(8)

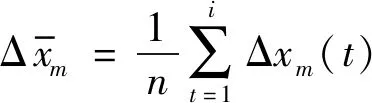
首先滤去了时间序列的平均值。由于一个时间序列可能有随机成分，把序列的这些成分过滤掉有助于后续分析。

(4) 序列重构

对具有N个数据的y(t)分别进行等长分割，以长度n将序列分割成m个不重叠的区间，其中

(9)

由于序列长度N并不总是长度n的整数倍，序列尾端有时会出现小部分的数据信息未能被利用。为了充分利用数据，对序列的颠倒顺序进行同样的操作，共得到m个等长度的区间。

(5) 对每个区间v，用最小二乘法对所包含的数据进行一阶线性拟合，如下

yv(i)=ayv+byv×i

(10)

式中：i=1,2,…,n;yv=1,2,…,m。

(6) 计算每个区间滤去趋势后的均方差。

(7) 对所有等长度区间求均值并开方，计算得到DFA波动函数。

(11)

(8) 如果时间序列x(t)长程幂律相关，则F(n)与n满足幂律关系。

在双对数坐标{lgn,lg[F(n)]}中做散点图，用最小二乘法拟合数据，其中直线部分的斜率即为超阶分析方法所得的信号标度律指数，记为α。

1.3 混合特征参数向量

超阶分析所得到的标度律指数可以作为表征故障信号故障信息的特征参数，突出信号序列本来的状态特征。因此，与1.1小节得到的常规信号特征参数(峭度因子、峰值因子、脉冲因子、裕度因子和波形因子)相结合，就可得到混合信号特征参数向量，作为滚动轴承智能故障诊断的特征向量。

2 混合特征驱动的滚动轴承智能故障诊断方法

2.1 改进的支持向量机

在利用SVM进行数据分类时，需设定两个重要参数：惩罚系数C和核函数参数γ。惩罚系数C决定对所取样本依赖程度，当C为无穷大时，所有样本将都满足约束，造成过拟合现象；而当C太小时，只有少数样本满足约束，导致欠拟合现象。γ是选择高斯核函数后自带的一个参数，代表着映射之后的空间分布。γ值越大，SVM个数越少，反之，γ值越小，SVM个数越多。γ值的选取对训练和预测速度有较大影响。为了实现参数自适应选取，本文采用PSO对SVM的参数进行优化选取。

PSO是从鸟类捕食行为的研究中发展而来，每个问题的解称为“粒子”，所有粒子的搜索空间都是N维的解空间，粒子优劣由适应度函数判定。每个粒子需保存自己搜索到的最佳位置，其速度根据其当前位置、其历史最优位置和群体最优位置动态调整[12-13]。粒子的速度和位置更新公式分别为

(12)

(13)

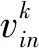
2.2 改进的支持向量机

信号故障特征提取与人工智能结合形成新故障诊断方法是智能故障诊断领域的一种趋势[14-16]。本文将构造的混合特征指标向量与ISVM相结合，形成基于混合特征向量和ISVM的滚动轴承智能故障诊断方法，其基本步骤为：

步骤1常规信号特征提取。将采集的信号分组，并标记每个分组的故障类别标签，对每个样本信号分别计算峭度因子、峰值因子、脉冲因子、裕度因子和波形因子。

步骤2标度律特征参数提取。按照超阶分析法的流程，提取每一个样本的标度律指数作为表征信号故障信息的特征参数。

步骤3混合特征向量构造。结合已提取的常规信号特征和标度律特征，构造混合特征参数向量。所有样本的特征向量构成一个特征矩阵，矩阵的每一行代表一个样本的特征集，依次为峭度因子、峰值因子、脉冲因子、裕度因子、波形因子和标度律指数属性值，特征矩阵的每一列样本的特征属性。

步骤4归一化。用最值归一化方法分别对特征矩阵的每一列进行归一化处理，并将归一化后的混合特征矩阵作为ISVM的输入。

步骤5模型训练。利用PSO对SVM的参数进行优化，用交叉验证法防止训练模型的过拟合，并将模型训练准确率用作判断模型训练好坏的标准，获得最佳模型参数。

步骤6智能故障分类。对测试数据进行类似处理，得到测试数据的特征集，用已获得分类模型对测试数据集进行智能故障分类。

提出的滚动轴承智能故障诊断方法框图，如图1所示。

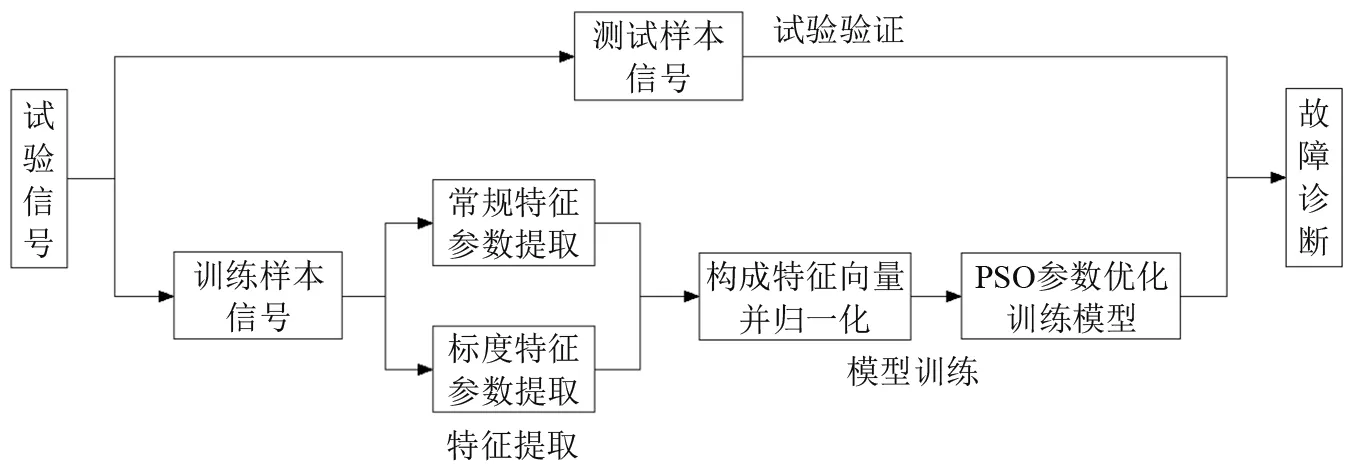
图1 提出的滚动轴承智能故障诊断方法框图Fig.1 Block diagram of the proposed intelligent fault diagnosis method for rolling bearing

3 试验验证

3.1 改进支持向量机有效性验证

采用UCI标准数据库中Wine数据集(网址：http://archive.ics.uci.edu/ml/datasets/Wine)对提出的ISVM的有效性进行验证，并与传统SVM方法性能进行对比。数据集的基本信息如表1所示。

表1 Wine数据集Tab.1 Dataset of Wine

粒子群算法的适应度函数取为支持向量机训练的准确率，提出算法优化过程的适应度曲线如图2所示。从图2中可知，第3代粒子最优适应度上升到92.7，第6代粒子最优适应度达93.26，此后迭代过程一直稳定在93.26保持不变。由图中平均适应度曲线可以看出，随着搜索得到的最佳适应度的稳步上升，当前迭代代数的平均适应度并不是线性上升的，而是呈现无规律的变化，说明C和g值对适应度的影响并不是线性变化的，一点小小的扰动就可能导致较大适应值的变化。

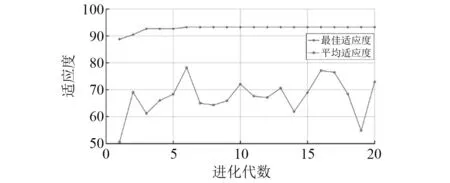
图2 粒子群算法适应度曲线图Fig.2 Fitness curve of particle swarm optimization algorithm

传统方法选取参数时，多采用网格搜索法，即用一个预先设置的网格去全域搜索k折交叉检验法下的最佳准确率。传统方法得到的最佳参数配合下的最佳准确率曲线，如图3所示。由图3可知，随着γ值的增加，所得模型训练的准确率在稳步上升。由传统方法得到的最佳准确率在90.45，小于ISVM所得到的最佳准确率，验证了提出方法的有效性。

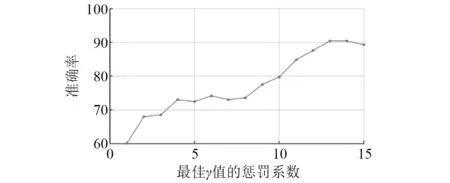
图3 传统方法准确率曲线图Fig.3 The accuracy curve of traditional method

3.2 滚动轴承故障模拟试验验证

采用QPZZⅡ型滚动轴承故障模拟试验台对提出滚动轴承智能故障诊断方法的有效性进行验证，试验台如图4所示。采集的数据有4种故障类型：正常、内圈故障、外圈故障和滚动体故障。每一类故障包含3个故障尺寸，0.2 mm，0.4 mm，0.6 mm，一共10类数据。每一个样本组的数据长度为1 000，各个样本组数据之间没有重叠。每一类数据有20个样本组，共计200个样本。

图4 QPZZⅡ型故障诊断试验台总体布置图Fig.4 Layout of fault diagnosis test bed of QPZZⅡ

按照7∶3的比例对样本数据集进行训练集和测试集的分组，即每一类标签数据中有14个样本作为训练集，6个样本作为测试集，数据分组情况如表2所示。

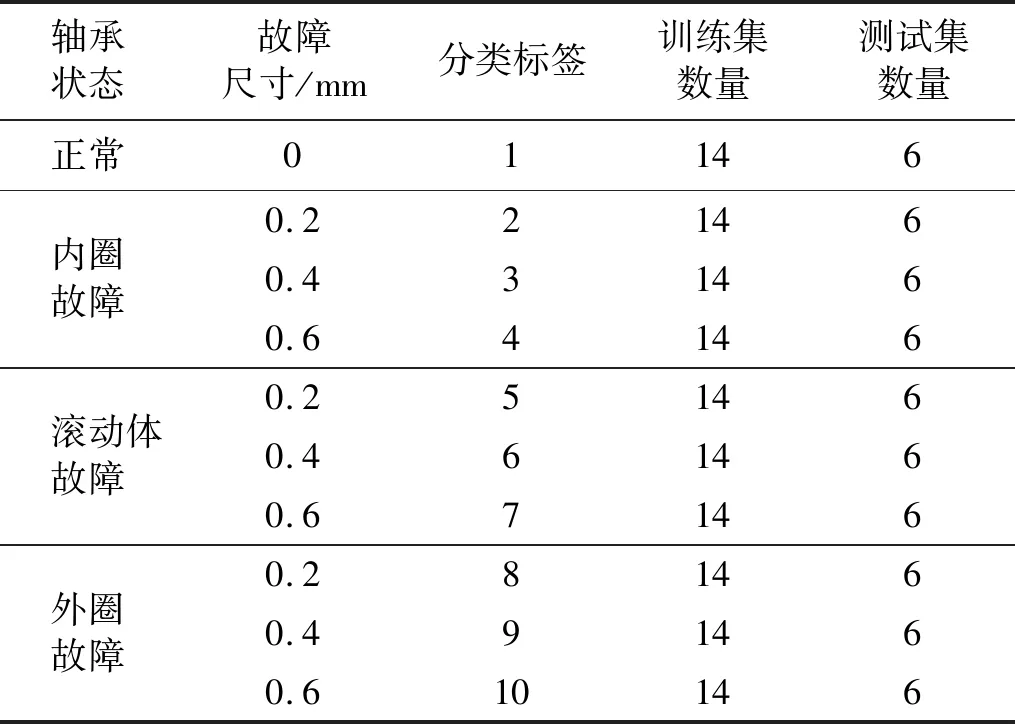
表2 滚动轴承数据集Tab.2 Dataset of rolling bearing

对每一个样本故障数据进行混合特征向量的提取，包括峭度因子、波形因子、峰值因子、脉冲因子、裕度因子和标度律指数。不同故障类型的标度律指数分布曲线图如图5所示。由图5可知，在同一故障类型和故障尺寸下不同样本间的标度律指数值波动较小，可以作为表征故障的特征指标。不同故障类型间相比较，不同故障类型故障信号的标度率指数均有一定的波动，但波动范围较小，不同的故障之间有较明显的区分，因此标度律指数可以作为特征指标对不同故障进行智能诊断。

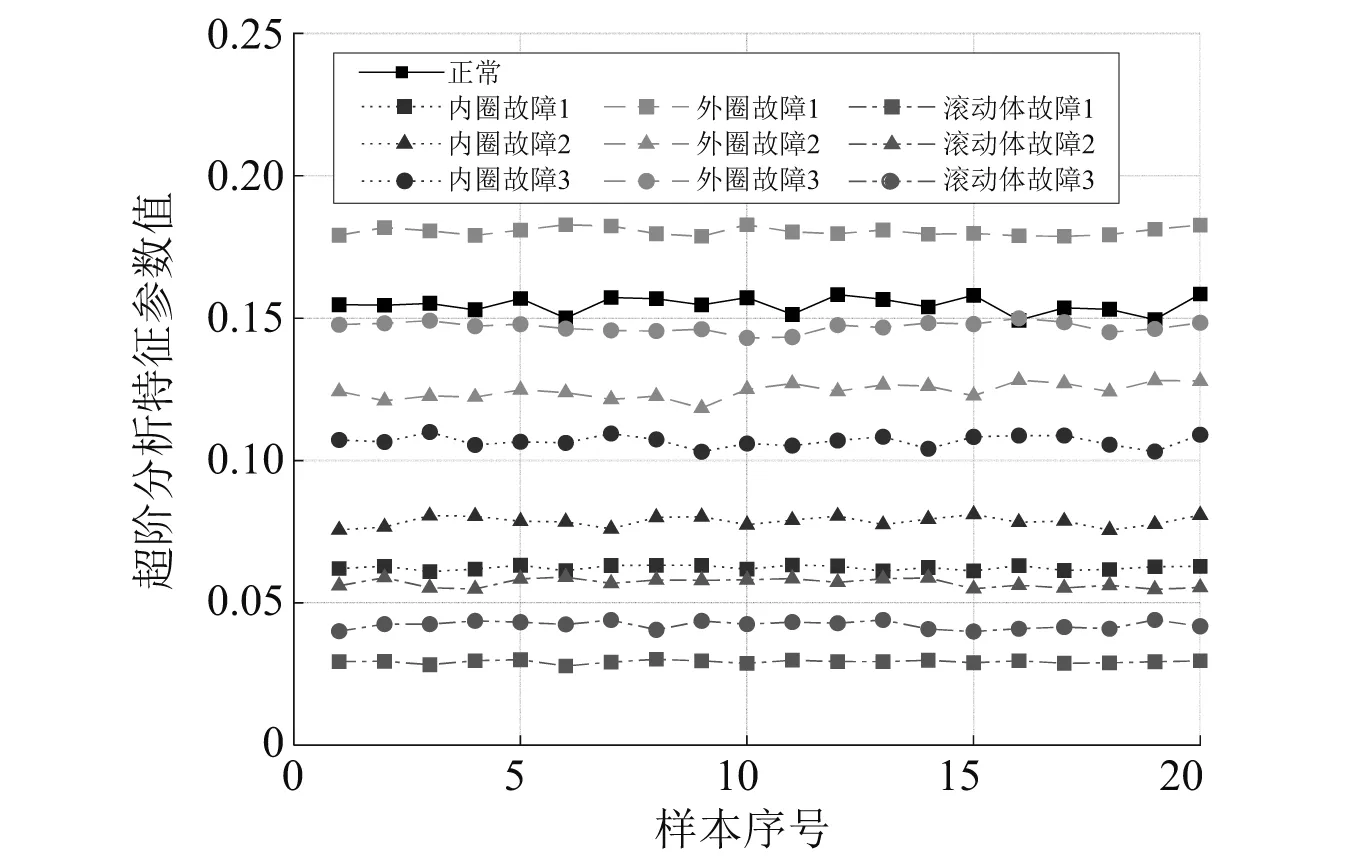
图5 不同故障类型的标度律指数分布曲线图Fig.5 Scale exponent exponential distribution curve of different fault types

将得到的标度律指数向量与常规特征指标向量结合组成混合特征矩阵，并将归一化之后的特征矩阵输入到提出的ISVM中。设置PSO参数为：c1=c2=1.5，粒子数量为20，速度更新的权重设置为线性递减权重，初始权重wstart=0.9，结尾权重为wend=0.4，按照迭代的次数进行权重的线性插值。SVM的惩罚系数范围为：Cmin=0.1，Cmax=1 000，径向基函数参数范围为：γmin=0.01，γmax=100。所得到的混合特征向量优化的支持向量机模型训练适应度曲线如图6所示。由图6中可以看出，第10代粒子的最佳适应度上升到90.71，此后基本保持稳定。最终得到分类模型的最佳参数为：Cbest=163.037，γbest=10.465。

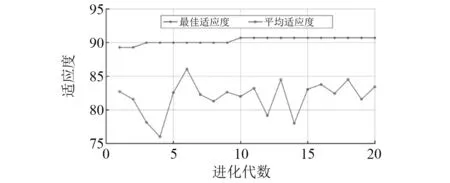
图6 基于混合特征的ISVM模型训练适应度曲线Fig.6 Training fitness curve of ISVM model based on hybrid characteristic vector

使用测试集对训练模型进行测试，结果如表3所示。由表3知，提出的滚动轴承智能故障诊断方法的分类准确率为96.67%，仅在标签6(滚动体故障，故障尺寸0.4 mm)的样本中出现了错分的情况，其他的故障类型分类准确率都达到100%。

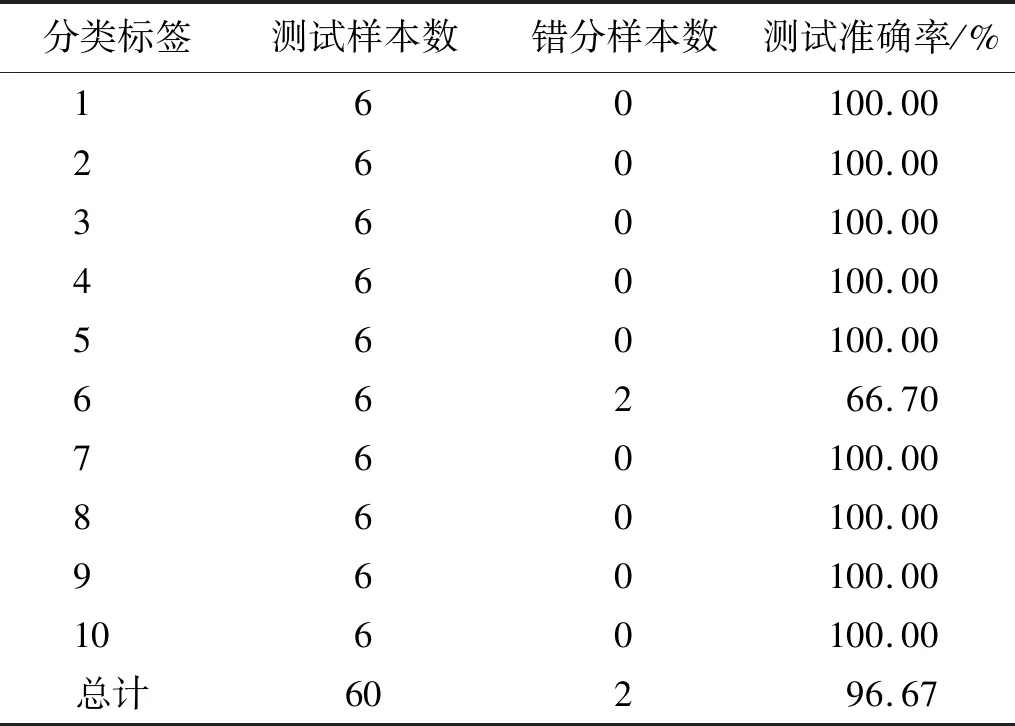
表3 混合特征优化的支持向量机故障诊断结果表Tab.3 Fault diagnosis results of SVM based on hybrid feature optimization

作为对比，仅采用1.1节介绍的常规无量纲特征指标作为故障特征，即峭度因子、峰值因子、脉冲因子、裕度因子和波形因子，采用同样的处理流程，将得到的常规特征参数矩阵输入到ISVM中，得到模型的训练准确率为77.86%，低于采用混合特征得到的训练准确率90.71%。使用常规特征和混合特征进行分类得到的测试准确率结果对比表如表4所示。由表4可知，使用常规特征的总体测试准确率仅为73.33%，低于使用混合特征得到的测试准确率，验证了提出方法的有效性。

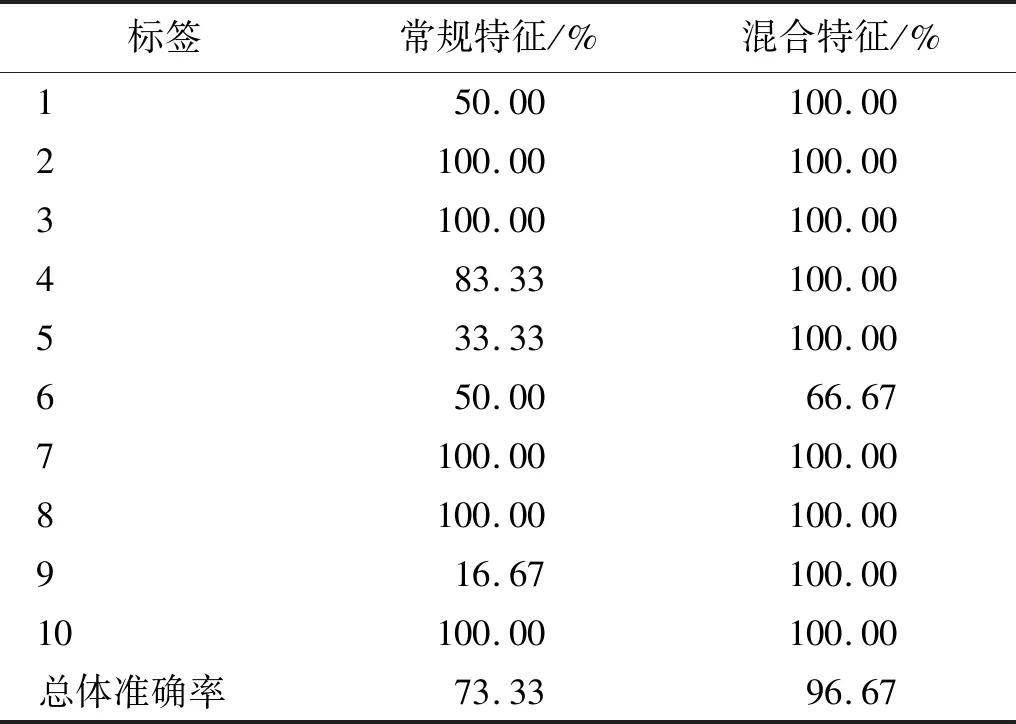
表4 两种故障诊断方法测试准确率结果对比表Tab.4 Comparison of test accuracy results of two fault diagnosis methods

4 结 论

采用超阶分析法获得分析信号的标度律指数，并结合常规无量纲参数构造了混合特征参数矩阵，进而采用ISVM实现滚动轴承故障智能诊断，结论如下：

(1) 提出ISVM法能够实现参数的自适应优化，相比于传统的网格搜索法，能获得更好的训练效果，提高模型的分类准确率。

(2) 由超阶分析得到的标度律特征可以作为表征故障的特征参数，通过与常规特征参数结合可以有效实现滚动轴承故障的智能诊断。与仅采用常规特征相比，提出方法得到的测试准确率增加了23%左右。

(3) 提出方法不仅能实现滚动轴承故障类型识别，而且能实现同一故障类型不同故障程度的有效识别。通过对故障程度更精细划分，有望实现故障程度的定量识别。