频变阻抗边界声空间特征频率灵敏度分析的有限元法

刘 强，梁梦辉，郑昌军，毕传兴

(合肥工业大学 噪声振动工程研究所，合肥 230009)

随着我国工业化进程的加速，噪声问题正日益受到重视。声学优化设计为结构的低噪声设计提供了一种有效思路，得到了越来越多的关注[1-3]。通常把声学优化设计按照设计变量的类型分为3个层次，即尺寸优化、形状优化和拓扑优化。灵敏度分析为基于梯度的优化方法提供了优化方向和量化依据，在声学优化设计过程中扮演着非常重要的角色[4-5]。

空腔噪声不仅会影响汽车等交通工具的乘坐舒适性，而且还可能会致使航天器内部的电子设备和结构发生失效和破坏。为了降低空腔噪声，工程中常采用在声腔边界铺设多孔吸声材料或吸声结构等方法。多孔吸声材料内部具有大量连通的孔隙，声波进入材料内部传播时能量会不断损耗，从而起到吸声作用。由于多孔吸声材料成本低且降噪效果明显，因此得到了广泛应用。为了便于处理，声学仿真分析中一般将多孔吸声材料等效为声场的阻抗边界条件[6-7]。通过声模态分析可以得到声腔特征频率和振型等信息，可以为吸声性能的考核、吸声结构的设计提供参考[8]。若将多孔吸声材料简化为常值阻抗边界条件，声模态分析求解的是常规二次特征值问题，可以采用子空间迭代或LANCZOS迭代等方法，计算效率高且适合大规模工程问题的求解。然而，由于多孔吸声材料结构复杂，吸声性能与材料的流阻率、孔隙率、厚度以及背板条件等诸多因素有关，因此通常具有频变特性，尤其是在低频段[9-10]。对于频变阻抗边界条件，声模态分析求解的是典型的非线性特征值问题[11]，求解过程复杂且现有主流有限元分析软件(如ANSYS、COMSOL Multiphysics等)尚不具有该功能。这也使在此基础上进行声模态的灵敏度分析变得更加困难。

对于非线性特征值问题的求解，近些年来基于围道积分法发展起来一类新的数值解法[12-13]。该类方法不需迭代，能够通过求解若干线性方程组将非线性特征值问题转化成规模很小的广义特征值问题，从而一次性地计算出选定复区间内的全部特征值和特征向量。该类方法的优势是计算精度高，且适合大规模并行计算。在前期工作中，本课题组已基于围道积分法发展了声模态的边界元分析方法[14]和声振耦合模态的有限元-边界元耦合分析方法[15]。然而，这些研究所求解的非线性特征值问题并不是由材料的频变特性所产生的，而只是由边界元系数矩阵的频率相关性所导致的。

本文针对由频变阻抗边界条件所导致的非线性特征值问题，基于声学有限元法构建了一种声学特征频率的灵敏度分析方法。首先，采用围道积分法将非线性特征值问题转换为规模很小的广义特征值问题；然后，通过对广义特征值问题的直接求导，构建声学特征频率的灵敏度分析方法。数值算例验证了该方法的准确性和适用性。

1 声学非线性特征值问题

当考虑非黏性理想声介质时，空腔Ω内的时谐声场的频域控制微分方程为

∇2p(x)+k2p(x)=0,x∈Ω

(1)

式中：∇2为拉普拉斯算子；p(x)为点x处的声压；k=w/c=2πf/c为波数；w为角频率；c为声速；f为频率。

为了降低空腔噪声，工程中常采用在声场边界铺设多孔吸声材料等方法。常用的多孔吸声材料有纤维板、泡沫铝、玻璃棉、聚氨酯海绵、泡沫塑料等，不同的多孔材料具有不同的吸声特性。多孔材料的吸声性能与材料的流阻率、孔隙率、厚度以及背板条件等因素有关，并且通常具有频变特性，特别是在低频段。当进行声学特性分析时，通常将多孔吸声材料等效为声场的阻抗边界条件。目前常用的等效模型有Delany-Bazley模型和Miki模型等。由这些等效模型得到的声阻抗均为频率的函数，因此相应的阻抗边界条件可以写成

(2)

采用加权余量法获得控制微分方程式(1)的等效积分弱形式，代入边界条件，再将声腔Ω进行单元离散，并对场变量进行插值近似，经整体组装后就可以得到声学有限元系统方程

(K+ikC-k2M)p=F

(3)

式中：K，C，M分别为声刚度矩阵、声阻尼矩阵和声质量矩阵；p为节点声压向量；F为声激励向量。声阻尼矩阵C与边界S上的声阻抗有关，K，M和C的单位矩阵具体形式分别为

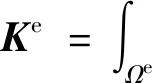
(4a)

(4b)

(4c)

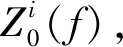
若令T(k)=K+ikC-k2M，则在声模态分析时，当齐次系统方程

T(λ)ψ=0

(5)

具有非平凡解，即当ψ≠0时，λ为特征值，相应的ψ称为特征向量。需注意本文中的特征值λ对应波数k，其与角频率w和频率f的关系为k=w/c=2πf/c。

由声阻尼矩阵C的单元矩阵计算式(4c)可知：当假设吸声材料的等效声阻抗为常值时，声阻尼矩阵C为常矩阵，此时式(5)所描述的声学特征值问题为一个常规的二次特征值问题；而当考虑更接近实际的频变声阻抗时，例如采用Delany-Bazley模型获得等效声阻抗值，声阻尼矩阵C则为频率的非线性矩阵函数，这就导致式(5)所描述的声学特征值问题成为一个典型的非线性特征值问题。相对于二次特征值问题，非线性特征值问题的求解要困难很多，目前仍缺少准确高效的通用数值解法，这也使在此基础上进行声学特征值的灵敏度分析变得更加困难。

2 非线性特征值的灵敏度分析

为了求解式(5)所描述的声学非线性特征值的灵敏度，本章首先基于近一二十年来发展起来的围道积分法将非线性特征值问题转化为易于求解的小规模广义特征值问题；然后，在此基础上构建一种声学特征值的灵敏度分析方法。该方法不需迭代，规避了传统迭代方法在求解非线性特征值问题时可能遇到的解的发散问题和计算成本过高等不足[16]。

2.1 非线性特征值问题的线性化

为实现非线性特征值问题的转化求解，我们首先在复平面内选取一个能够包围待求特征值区间的封闭曲线C，然后形成如下一类矩阵

(6)

通过矩阵M可以构造出块对称的Hankel矩阵H1和H2，即

(7)

(8)

由Asakura等的研究可知，矩阵H2相对于H1的广义特征值等价于原始非线性特征值问题式(5)在封闭曲线C内的特征值。若用λj表示封闭曲线C内的第j个特征值，vj为特征值λj对应的特征向量(若无指出，以下特征向量均指右特征向量)，那么H2相对于H1的广义特征值问题可以表示为

(H2-λjH1)vj=0

(9)

式(9)描述的广义特征值问题可以很容易地转换为标准线性特征值问题进行求解，在求得特征值和对应的特征向量后，式(5)的原始特征向量ψj可由特征向量vj通过

ψj=Svj

(10)

计算得到。这里的矩阵S=[S0,S1,…,SK-1]，其中的子矩阵S为

(11)

对比矩阵H1，H2和T的阶数，可以发现转换后的广义特征值问题的规模要远小于原非线性特征值问题的规模，因此式(9)描述的广义特征值问题能够快速地求解。另外，在计算矩阵M和S时，参数K和L的选取以及特征值数目m的确定可以参考Zheng等的研究。

2.2 单特征值的灵敏度分析

对于单特征值(即代数重数为1的特征值)，为了求其对任意设计变量的灵敏度值，我们将转换后的小规模广义特征值问题，即式(9)，直接对设计变量求导得到

λ′jH1vj=(H′2-λjH′1)vj+(H2-λjH1)v′j

(12)

式中，()′=∂()/∂ϑ为对设计变量ϑ的导数。此处的设计变量ϑ可以为形状参数、材料属性参数、拓扑参数等，本文侧重于形状参数的灵敏度分析。

由于式(12)中的λ′j和v′j皆未知，因此无法直接进行求解。为此在求解之前，对其增加约束条件，若采用最大归一化方法将特征向量vj正则化后再对设计变量求导[17]，可以得到

Өjv′j=0

(13)

式中，Өj={0,…,σ,…,0}为KL阶权重向量，σ为第e个位置的非零任意常数，e为原特征向量vj绝对值最大的元素的位置。

联立式(12)和式(13)可以得到

(14)

可以证明，式(14)的系数矩阵为满秩矩阵。因此，单特征值λj的灵敏度值λ′j可以通过求解式(14)得到。

2.3 重特征值的灵敏度分析

对于重特征值λ，若假设其代数重数为r(r>1)，那么该重特征值及其对应的右特征向量应满足

H2X=H1XΛ

(15)

式中：X为λ对应的所有右特征向量组成的KL×r阶矩阵；Λ=λI为r×r阶对角矩阵，I为单位矩阵。显然，X的列向量张成的向量空间中的任意向量都是λ对应的特征向量，但并不是所有特征向量都满足随设计变量连续变化的要求，因此，若仍采用式(14)计算重特征值λ对应的灵敏度值，将可能会导致计算结果的不准确。

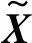
(16)

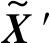
(17)

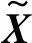
WΓ=ΓΛ′

(18)

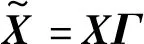
注意到式(14)和式(18)中包含Hankel矩阵H1和H2对设计变量的导数，根据式(7)和式(8)可知

(19)

(20)

由于随机矩阵U和V与设计变量无关，因此矩阵M对设计变量的导数为

(21)

式中，Tn(z)=-T(z)-1T′(z)T(z)-1，T′(z)为有限元系数矩阵T(z)对设计变量的导数。当考虑的设计变量与频率无关时，T′(z)为

T′(z)=K′+izC′-z2M′

(22)

此处的K′=∂K/∂ϑ，C′=∂C/∂ϑ，M′=∂M/∂ϑ，为了简便一般可以通过差分方法计算得到。然而，差分方法的计算精度受差分步长影响，且由于需要多次计算系数矩阵也影响了计算效率。为了更准确、高效地计算这些导数矩阵，本文采用直接微分方法，直接对声刚度矩阵、声阻尼矩阵和声质量矩阵求设计变量的导数，从而得到导数矩阵的解析表达式，类似过程可以参考Wang等[18]的研究中关于结构刚度矩阵对设计变量导数的计算过程，这里不再赘述。

注意到式(6)、式(11)和式(21)中需要计算一系列形如

(23)

的围道积分。当关注的特征值区间为[λmin,λmax]时，若选取椭圆作为积分路径，且椭圆的长轴和短轴分别与复平面的实轴和虚轴平行，并且采用NS点梯形公式进行数值积分，式(23)可以转换为

(24)

式中：ρ=(λmax-λmin)/2为椭圆长半径；γ=(λmax+λmin)/2为椭圆圆心；ζ为椭圆的短轴和长轴的比值；zt=γ+ρ(cosθt+iζsinθt)；θt=2π(t-1/2)/NS。当ζ=1时，椭圆即成为圆形；当关注的特征值为实数或离实轴很近时，可以采用较小的ζ，例如ζ=0.1。需要注意的是：式(24)对积分路径进行了平移和缩放，基于其得到的广义特征值问题的特征值τj还需通过

λj=γ+ρτj

(25)

变换成原始特征值，同理需要通过

λ′j=ρτ′j

(26)

得到原始特征值的灵敏度值。

2.4 算法的实现步骤

基于2.1节～2.3节的内容，我们可以构建复杂频变阻抗边界下的声学特征频率灵敏度的计算算法，具体如下：

输入：NS，K，L，γ，ρ，ζ

输出：λj，λ′j，ψj，j=1,2,…,m

(1) 初始化随机矩阵U和V；

(2) 计算矩阵M，M′和S(=0,1,2,…,2K-1)；

(3) 组装Hankel矩阵H1，H2，H′1，H′2和转换矩阵S；

(4) 求解H2相对于H1的广义特征值问题，得到λj，uj和vj(j=1,2,…,m)；

(5) 统计单特征值的数目，记为p，将所有的重特征值及其特征向量置后；

(6) fork=1,2,…,p

(7) 按最大值归一化法对vk进行正则化处理，并记录最大值的位置e；

(8) 构造权重向量Өk，组装成系统方程式(14)；

(9) 求解式(14)得到λ′k；

(10) 通过式(10)计算出ψk；

(11) end for

(12) 对每个不同的重特征值，分别求解式(18)和式(10)，重特征值对应的灵敏度及其特征向量。

3 数值算例

本章将使用两个数值算例来验证本文所构建的声学特征频率灵敏度分析方法的准确性和适用性：第1个算例为具有解析解的二维圆环模型；第2个算例为三维消声器模型。所有计算程序均采用FORTRAN 90编写，有限元系数矩阵采用压缩稀疏行(compressed sparse row,CSR)格式存储，并通过Intel MKL提供的PARDISO求解器求解有限元稀疏线性方程组以形成矩阵M，M′和S。算例中的声介质均为空气，其密度ρm=1.2 kg/m3，声速c=340 m/s。算例采用在多孔吸声材料建模中广泛应用的Delany-Bazley模型获得等效的声场阻抗边界条件，如对于厚度为h且具有刚性背板的多孔吸声材料，由Delany-Bazley模型得到的表面声阻抗为

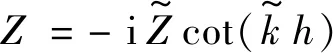
(27)

其中，

(28)

(29)

式中：δ=ρmf/Rf，Rf为多孔材料的流阻率。若h=0.1 m，Rf=10 000 Pa·s/m2，由式(27)得到阻抗Z随频率f的变化曲线如图1所示(为显示起见，图中虚部值为原阻抗虚部值的相反数)。从图1中可以看出，阻抗Z随频率f的改变而变化，在0～500 Hz尤为明显，因此在声模态分析中考虑频变阻抗是很有必要的。

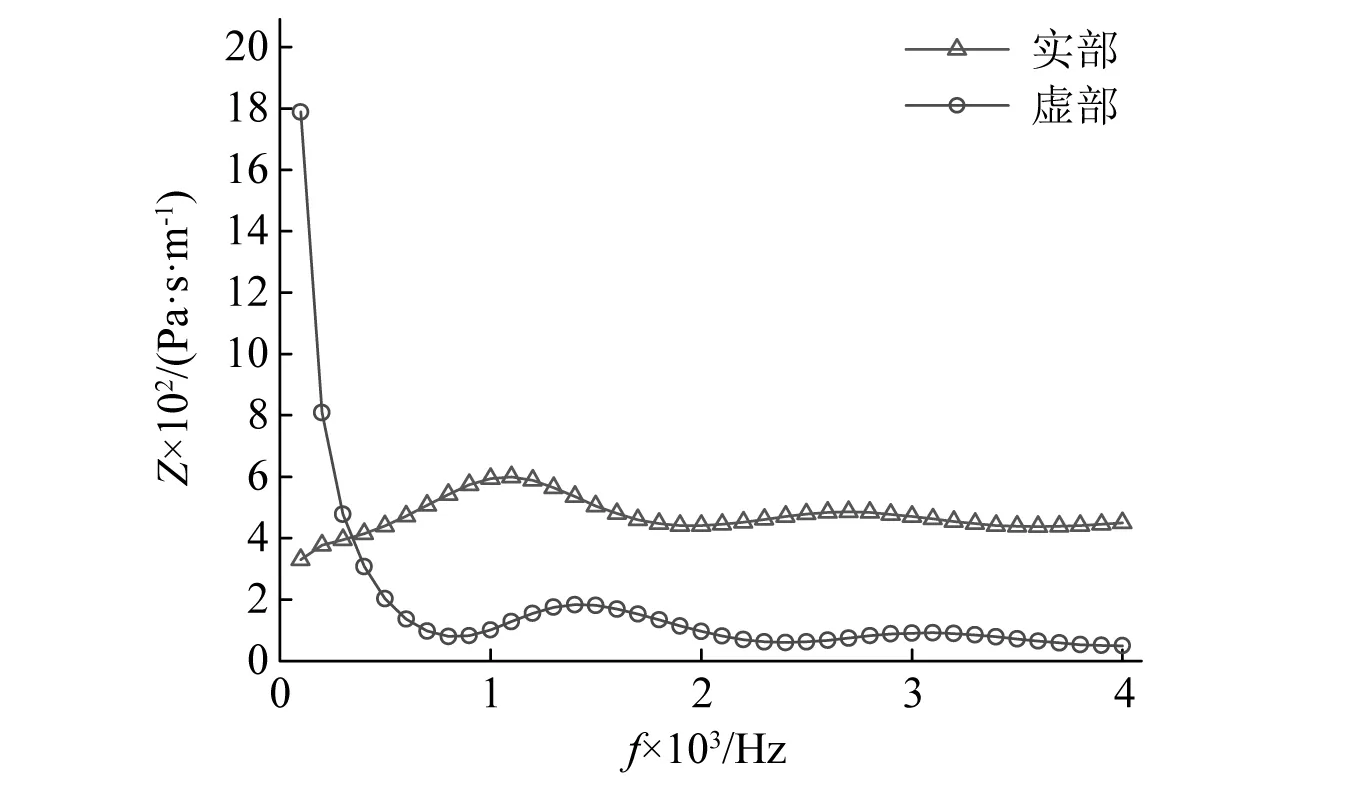
图1 阻抗曲线图Fig.1 The curve of acoustic impedance

3.1 二维圆环模型

二维圆环模型的示意图如图2所示，图2中的r和R分别为圆环的内径和外径。该模型具有解析解，常用作汽车轮胎内声腔的二维简化模型。汽车轮胎内声腔的共振会致使车内噪声在200～250 Hz出现一个明显峰值[19-20]，工程中常采用在轮胎壁面铺设多孔吸声材料的方法加以解决。圆环模型的内边界代表轮辋，设置为刚性边界；外边界代表轮胎壁面，由于铺设多孔吸声材料的缘故，设置为阻抗边界。该模型的解析特征值为满足方程

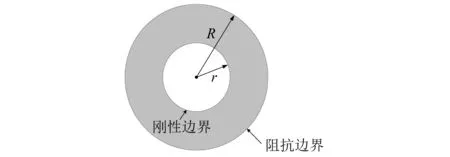
图2 二维圆环模型示意图Fig.2 The 2D circular model

J′n(kr)[Yn(kR)-iZ0Y′n(kR)]-Y′n(kr)[Jn(kR)-iZ0J′n(kR)]=0

(30)

的k值(此处的k为波数，需注意以下特征频率皆以波数形式给出，为了以示区别我们统一称之为特征值)。式(30)中：Jn和Yn分别为n阶第一类和第二类贝塞尔函数；J′n和Y′n分别为Jn和Yn的一阶导数。

在数值仿真中，圆环的外径R=1 m，内径r=0.5 m；多孔吸声材料的厚度h=0.1 m，流阻率Rf=10 000 Pa·s/m2。圆环域共离散成1 465个四边形二次声学单元。围道积分路径选取参数为γ=(3.9,0.5)，ρ=1.8和ζ=0.5的椭圆，梯形积分点数NS=150，参数K和L分别设为7和4。

特征值的计算结果及其实部和虚部的相对误差，如表1所示。从表1中可以看出，除了第11个特征值为单特征值外，其余皆为重特征值。第1、第3、第5、第7、第11和第12个特征值对应的振型如图3所示。从表1中还可以看出，本文所构建的声学非线性特征值分析方法对单特征值和重特征值均可以给出非常准确的计算结果，且所有特征值都具有正虚部，该虚部反映了多孔吸声材料对声场的衰减作用，可以用作多孔吸声材料流阻率等参数的选取判据。特征值灵敏度的计算结果及其实部和虚部的相对误差，如表2和表3所示。其中：表2是以内径r作为设计变量；表3是以外径R作为设计变量。从表2和表3中可以看出，随着特征值的增大，计算结果实部和虚部的相对误差逐渐变大，但整体误差水平都很低，这表明本文所构建的分析方法可以准确地计算出声学特征频率的灵敏度值。

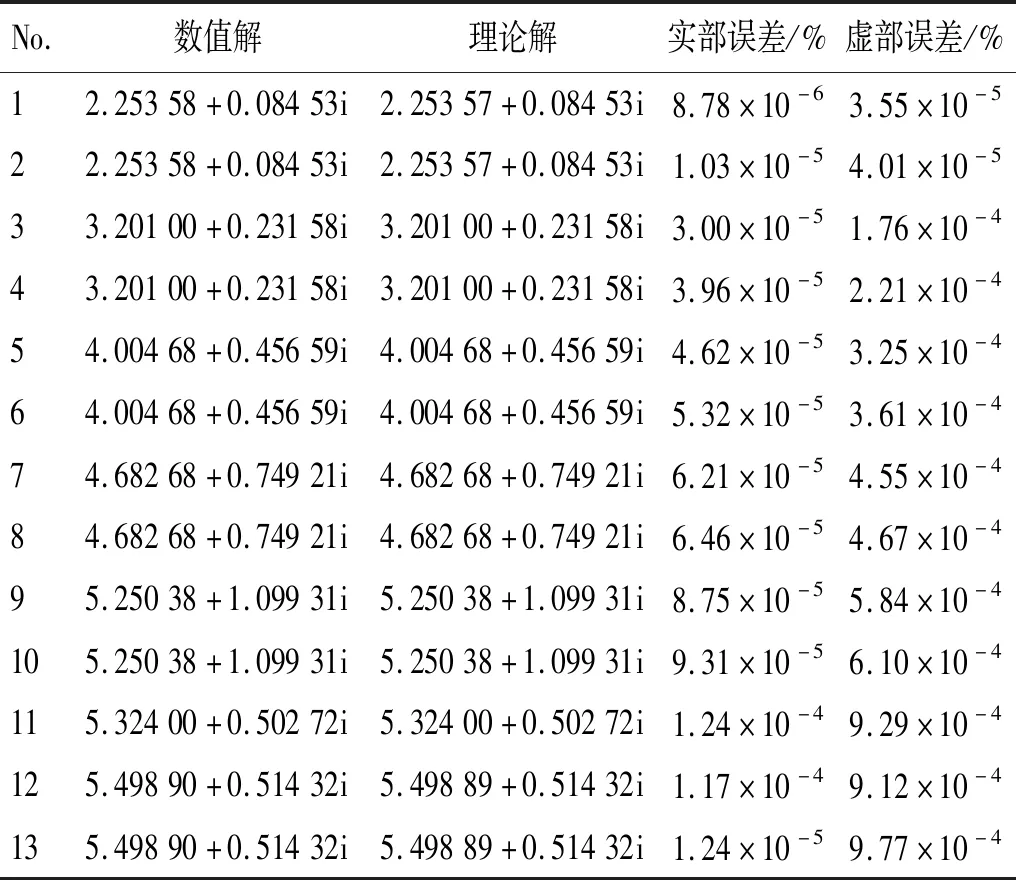
表1 数值特征值及其相对误差Tab.1 Numerical eigenvalues and their relative errors

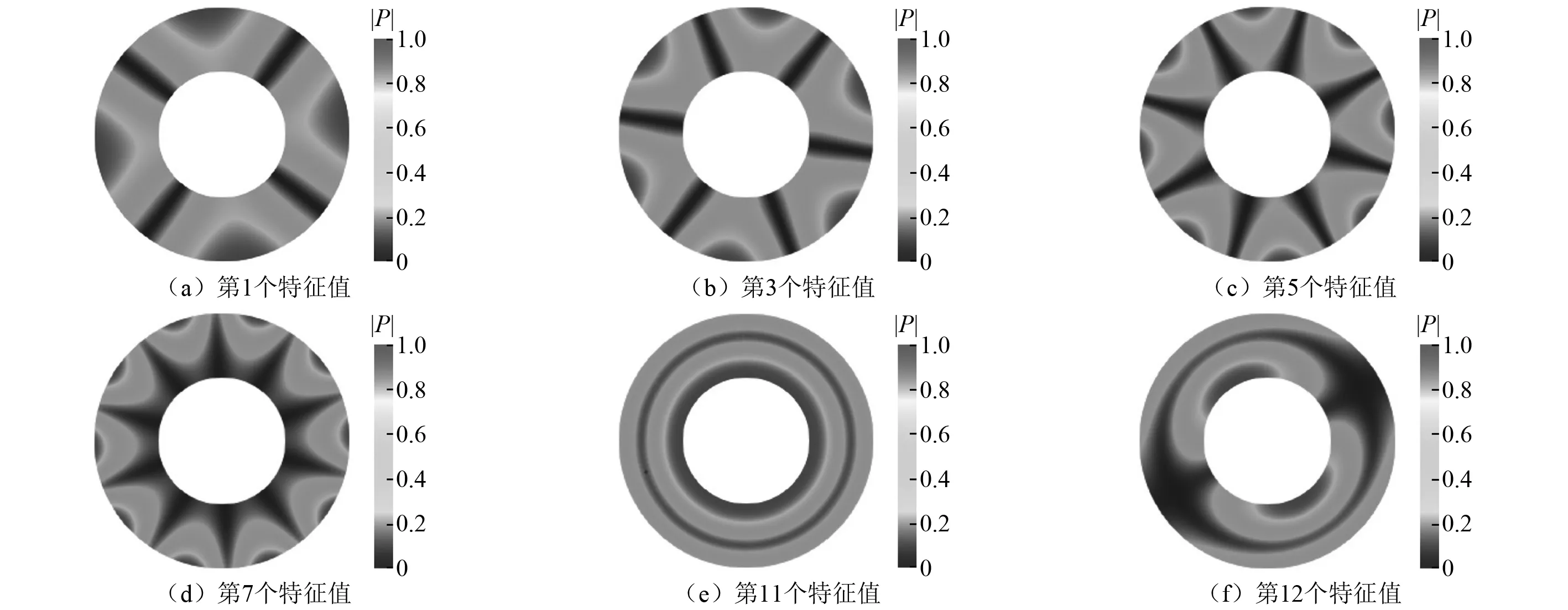
图3 圆环形空腔部分振型图Fig.3 Eigenmodes of the circular model

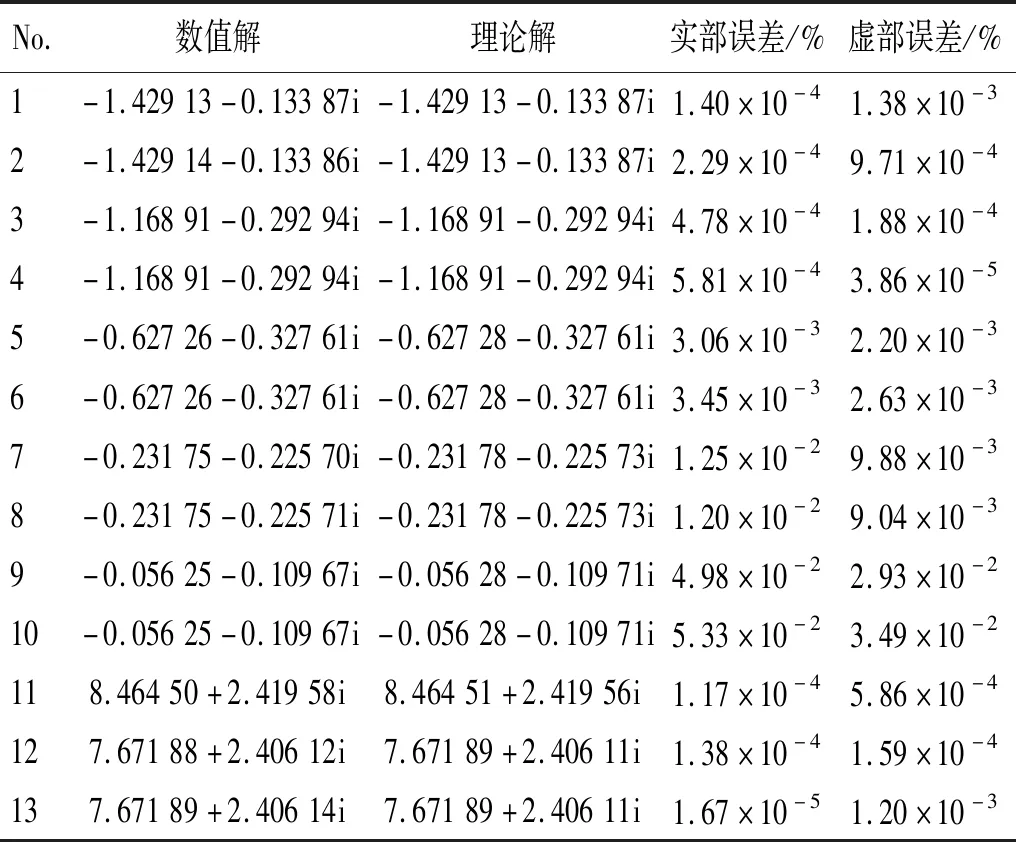
表2 特征值灵敏度及其相对误差(内径r为设计变量)Tab.2 Eigenvalue sensitivities and their relative errors (the design parameter is the inner radius r)

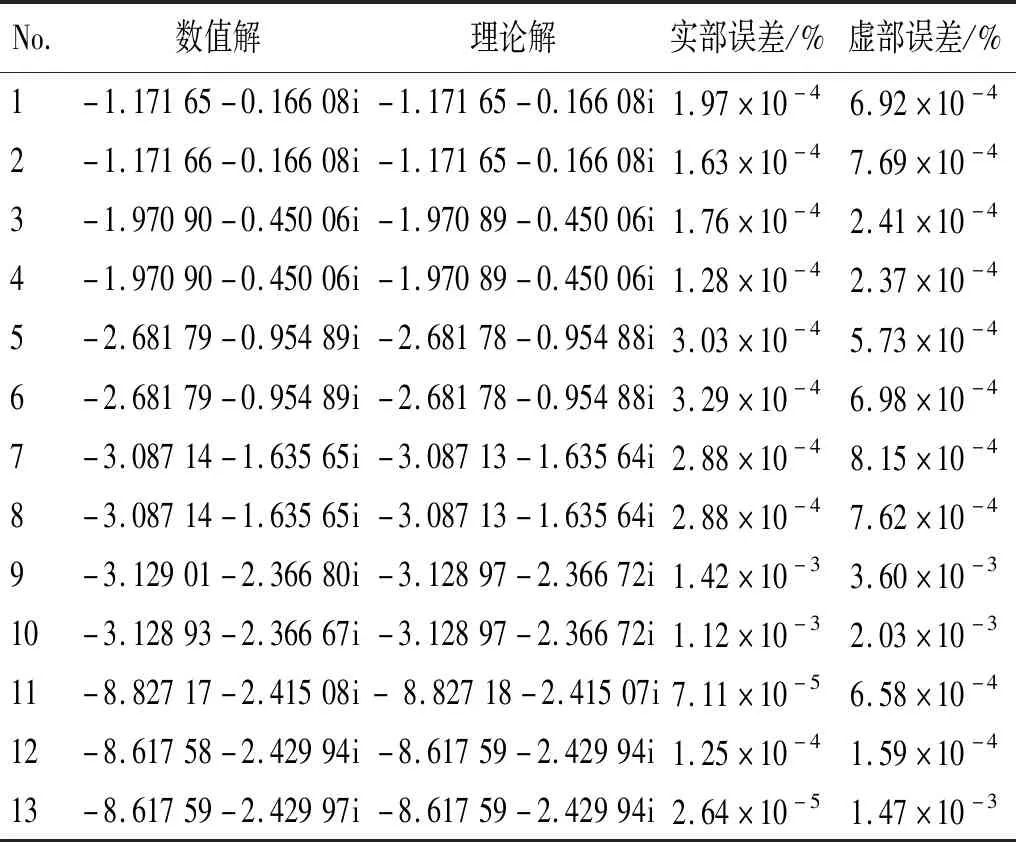
表3 特征值灵敏度及其相对误差(外径R为设计变量)Tab.3 Eigenvalue sensitivities and their relative errors (the design parameter is the outer radius R)

3.2 消声器模型

本算例通过如图4所示的消声器模型进一步验证本文构建的声学特征频率灵敏度分析方法在工程问题中的适用性。消声器轴向的最大尺寸为0.9 m，截面宽和高的最大尺寸分别为0.30 m和0.15 m，沿轴线方向的两个排气管的半径为0.04 m，长度为0.15 m。为了提高降噪性能，在消声器共振腔沿排气管轴线方向的周向内壁铺设有多孔吸声材料。不同于算例1采用声腔的形状参数作为设计变量，本算例将采用多孔吸声材料的厚度作为设计变量。

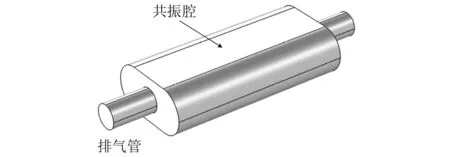
图4 消声器模型示意图Fig.4 The muffler model

多孔吸声材料的厚度h=0.015 m，流阻率Rf=1 424.2 Pa·s/m2，在数值仿真中，同样采用Delany-Bazley模型将铺设多孔吸声材料的壁面等效为声学阻抗边界，而其余壁面设置为声学刚性边界。经有限元网格划分后，声场域共离散成4 575个四面体二次声学单元。围道积分路径选取圆心γ=(9.1,0.2)、半径ρ=5.0的圆形，梯形积分点数NS=150，参数K和L分别设为5和4。在灵敏度分析中，取多孔材料的厚度h为设计变量。由于该算例没有解析解，因此采用差分法计算得到灵敏度的参考值，差分步长设置为h/105。特征值及其灵敏度的计算结果，以及灵敏度的差分参考值，如表4所示。部分振型图如图5所示。从表4中可以看出，本文构造的声学特征频率灵敏度分析方法的计算结果与差分方法得到的参考值非常接近。然而相比差分法，本文方法不存在步长敏感和反复计算等问题，具有更好的准确性和适用性。

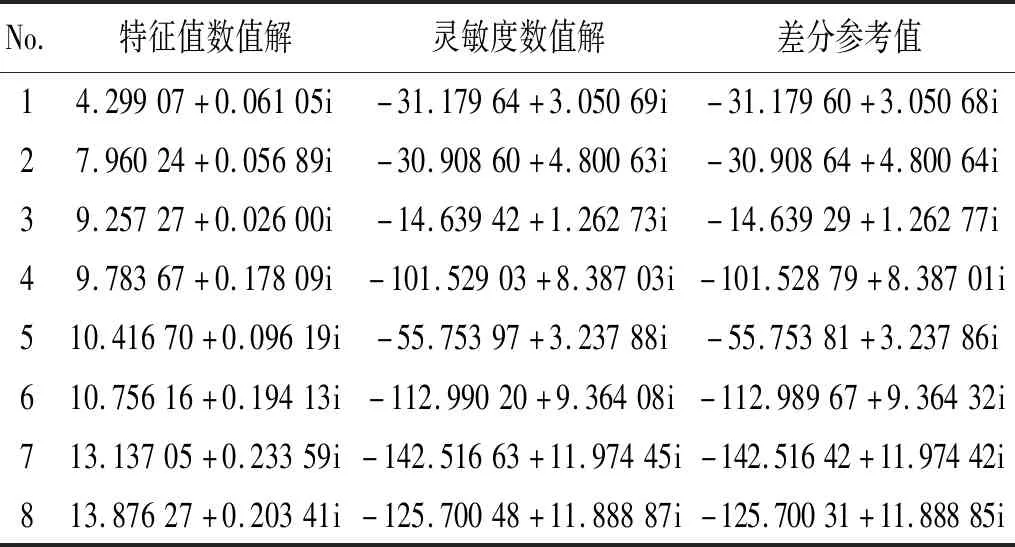
表4 消声器模型的特征值及其灵敏度Tab.4 Eigenvalues and their sensitivities of the muffler model

图5 消声器模型的部分振型图Fig.5 Eigenmodes of the muffler model

4 结 论

针对铺设多孔吸声材料声空间的优化设计，本文基于声学有限元法，构建了一种声模态特征频率灵敏度分析的数值方法，为计算声学非线性特征值灵敏度提供了一种新思路。该方法首先通过围道积分法将复杂的非线性特征值灵敏度问题转化为规模很小的广义特征值灵敏度问题；然后一方面通过对右特征向量正则化处理实现单特征值灵敏度的计算，提高了方法的计算效率；另一方面采用重构右特征向量空间的方法实现重特征值灵敏度的计算，拓展了方法的应用范围。数值算例验证了该方法的求解精度和适用性，以及在工程问题中的应用潜力。另外，该方法还可以很容易地推广到声振耦合问题[21-22]的特征频率灵敏度分析中去。