直接基于谐波电动势定向的PMSM转矩脉动抑制方案研究
杨淑英, 储昭晗, 房佳禹, 谢震
(合肥工业大学 电气与自动化工程学院,安徽 合肥 230000)
0 引 言
永磁同步电机(permanent magnet synchronous machine,PMSM)的高功率密度和高效率特点使其广泛应用在新能源汽车、航空航天、伺服系统等领域[1]。然而,在实际应用中由于电机自身结构的非理想特性、磁饱和特性、装配误差、以及控制上的电流偏差、谐波等因素,使得永磁同步电机尤其是内置式永磁同步电机易受到转矩脉动的困扰,影响了其运行性能[2]。转矩脉动一方面会产生电磁噪声,降低驱动系统的控制性能,使电机运转过程中出现转速波动;另一方面,若电机转矩脉动频率与机械传动系统的共振频率接近,会引起传动系统显著的扭转振动,降低整车驾乘的舒适性和系统可靠性,甚至引发传动系统失效[3]。因此,抑制转矩脉动,提高驱动系统转矩品质尤其在新能源汽车场合有着重要的研究价值,近年来也受到广泛的关注[4]。
针对电磁转矩脉动的抑制,当前所采取的技术方案大体可以划分为两类:一是从电机本体结构设计和优化角度来降低电磁转矩的脉动,二是通过控制算法设计实现转矩脉动的抑制[5]。从电机本体设计上抑制转矩脉动方案,不仅会增加电机设计、制造复杂性,增加制造成本,而且会影响电机的功率密度[6]。另外,电机本体的优化设计无法克服驱动控制器谐波所引发的转矩脉动[7]。而从控制的角度主动进行转矩脉动抑制,尽管受制于转矩脉动信息检测、控制误差等因素难以完全消除,但相比而言具有较强的灵活性和适用性[8]。从控制器自身的发展来看,其算法本身也应该能够对电机绕组分布和磁密特性等具有较强的适应性,这也为从控制的角度探讨转矩脉动抑制方案提出了技术需求。控制算法抑制转矩脉动的思路是通过在电机定子回路中主动产生谐波电流以抵消磁链谐波所造成的谐波转矩[9]。
基于控制算法的转矩脉动抑制方案其关键在于转矩脉动信息的提取以及注入谐波的生成。直接依据磁链谐波模型计算转矩脉动量,受参数影响较大,且参数的非线性特征使其难以准确获得[10]。文献[11-12]通过设计自适应观测器,对磁链脉动量进行观测,依然具有较强的参数依赖性,且对观测器的动态性能要求较高,容易受到噪声干扰。有限元仿真的方法能够较好地获得磁链脉动信息,进而获得转矩脉动量[13-14]。然而,仿真所需的结构、尺寸信息难以准确获得,且电气模型难以反映检测、装配误差等因素引起的转矩脉动。文献[15]通过实测数据依据工作点和位置信息查表的方式获得转矩脉动量,数据表的生成较为耗时,且大量的查表运算影响到算法的执行效率。文献[16]通过设计安装压电传感器,进行振动噪声检测,进而获取转矩脉动信息,但这一方面对检测电路的噪声抑制能力和带宽有着较高的要求,另一方面,其安装场合受限。文献[38-39]通过比例积分(proportional-integral,PI)调节器并联谐振控制器的方式实现对定子电流谐波的抑制,以期减小转矩脉动。实际上,通过分析不难发现只要磁链中含有谐波,其与定子电流基波的作用依然会产生转矩脉动。文献[40]在基于磁共能模型,通过反推计算获得转矩脉动抑制电流,实现转矩脉动抑制。电磁转矩的脉动会引起速度的脉动,基于速度脉动信息的机械模型方案,相比而言具有较强的参数鲁棒性[17]。然而,基于速度脉动信息提取转矩脉动属于一种间接获取方式,如何基于该信息获取优化的谐波电流信息以实现转矩脉动的抑制,依然具有挑战。实际上,在获得脉动量后,如何生成用于脉动量抑制的谐波电流控制量,也是学界研究的热点。
文献[18]采用模型预测控制(model predictive control,MPC)实现转矩脉动量的抑制,文献[19]通过输入输出线性化,依据磁链脉动信息直接获取补偿电压的方式实现转矩脉动的抑制。在矢量控制方案的基础上,文献[20]通过比例方法直接生成所需注入的谐波电流,忽略了相位差的影响。文献[21]通过对转矩脉动量幅值和相位解耦控制的方式,获取谐波电流的幅值和相位,但需要d、q轴谐波电流满足特定的关系。文献[22-23]通过人工神经网络,文献[24]通过迭代学习的方式获取优化的谐波电流注入,但其工程实现较为复杂。文献[28]通过注入试探电流的方式计算谐波电流指令,其在稳态条件下具有较好的适应性。
纵观文献报道不难发现,尽管通过转速脉动量的提取能够反映转矩的脉动,但谐波电流相位的设定依然缺少理论依据。智能算法理论上能够通过自学习的方式试探出待注入的谐波电流相位,但工程实现较为复杂。本文通过数学模型的推导和谐波转矩的计算,从理论上证明待注入谐波电流的相位与谐波电动势(electromotive force,EMF)的相位相同,为谐波电流指令的生成提供理论依据。基于此,本文提出一种直接基于谐波电动势定向的PMSM转矩脉动抑制方案。该方案通过扩张状态观测器(extended state observer,ESO)的设计实现谐波电动势的观测,进而获得注入谐波电流的定向角,通过转速脉动量的检测和闭环调节器的设计获得注入谐波电流的幅值,提升转矩脉动抑制的鲁棒性。最后,论文通过实验验证本文的分析和设计。
1 转矩脉动抑制方案理论分析
考虑到永磁体磁链谐波的影响,永磁同步电机在dq旋转坐标系下的数学模型可表示为[26]:
(1)
(2)
(Ld-Lq)idiq];
(3)
(4)
其中:Rs为定子电阻;Ld和Lq分别为d和q轴电感;ωe为电气角速度;ωm为机械角速度;θ为电角度;J为转动惯量;ψd0为永磁磁链直流分量;ψdk和ψqk为第k次磁链谐波分量幅值;φψk为第k次磁链谐波分量相角。
由式(2)和式(3)可以看出,受磁链谐波的影响电磁转矩中将出现基波6倍频次的高次脉动,且由式(4)可以看出,电磁转矩脉动将会引起转速的同频次脉动。将式(4)中的电磁转矩和转速表述为直流分量和脉动分量之和的形式,即:
(5)
其中:Tek和φTk为k次转矩脉动的幅值和相角,ωmk和φωk为k次转速脉动的幅值和相角。假设负载转矩无谐波,将式(5)代入式(4)中并分离直流量与各次交流量,稳态情况下有:
(6)
可见,k次转矩脉动幅值与k次转速脉动幅值成正比,比例系数为kωeJ。转矩脉动对转速脉动的影响与转速大小成反比,即相同的转矩脉动对低速运行影响较大。
令d轴和q轴电动势为
(7)
则式(3)可表示为
Te=1.5[edid+eqiq+ωe(Ld-Lq)idiq]/ωm。
(8)
其中:1.5[edid+eqiq]/ωm为永磁体转矩;1.5[ωe(Ld-Lq)idiq]/ωm为磁阻转矩。
电磁转矩可以看作是电动势与定子电流相互作用的结果,同频率分量相互作用产生常值转矩,而不同频率分量相互作用则产生脉动转矩[33]。假设定子电流中不含谐波,则由谐波电动势产生的转矩脉动可表示为[9]
(9)
其中:id0、iq0分别为d、q轴电流直流分量;edk和eqk分别表示k次谐波电动势的d和q轴分量,其量值可由式(7)计算获得,即将式(2)谐波磁链代入式(7)得:
(10)
为便于表述,将式(10)简记为:
(11)
其中:Ek、θek分别表示k次谐波电动势的幅值和相角,其与式(10)中磁链的幅值和相角间的关系可表示为:
(12)
将式(11)代入式(9)并进行三角函数化简运算,可将谐波电动势与基波电流作用所产生的转矩脉动表示为
(13)
其中:I0和θi0分别为电流基波的幅值和相角,即:
(14)
由式(13)不难发现对电驱动系统而言,即使完全消除定子电流中的谐波,若磁链中存在谐波,将导致电动势中含有谐波,最终使得电磁转矩中依然会存在脉动[31],且在一定的电流下,脉动幅值与谐波电动势幅值成比例。为抑制谐波电动势产生的转矩脉动,可以在定子电流中注入对应频率的谐波,其与基波电动势的作用也将产生转矩脉动,若注入的谐波电流的幅值和相位合适将能够抵消谐波电动势转矩脉动。图1示意了电动势和电流矢量的相位关系及其产生的电磁转矩。显然,通过注入谐波电流幅值和相位的设计,其与基波电动势和基波电流相互作用产生的脉动转矩Tecom能够补偿谐波电动势产生的脉动转矩Teψ。
这里不妨令注入的k次d和q轴补偿电流分别为:
(15)
其中:Ik和θik分别表示k次补偿电流的幅值和相位。将式(15)代入式(8),对应k次谐波电流的转矩脉动可表示为
Tecom=1.5[ed0idk+eq0iqk+
ωe(Ld-Lq)(id0iqk+iq0idk)]/ωm。
(16)
其中:ed0和eq0分别表示转子磁链定向同步旋转dq坐标系下基波电动势的坐标轴分量,在稳态情况下有:
(17)
将式(17)代入式(16),并进行三角函数化简运算可得
(18)
其中:
(19)
若要实现转矩脉动的抑制,需要满足
Tecom+Teψ=0。
(20)
将式(13)和式(18)代入式(20),并令对应次脉动量相互抵消,可得
(21)
令式(21)等式两边的幅值和相位对应相等,可得为抑制转矩脉动所需注入的电流谐波应满足的条件:
(22)
(23)
将式(14)中θi0的表达式和式(19)中θMN的表达式代入式(23)并化简可得
(24)
对内置式永磁同步电机通常采用最大转矩电流比(maximum torque per ample,MTPA)控制,此时d和q轴电流分配关系为:
(25)
为了便于表述,令
(26)
将式(25)和式(26)代入式(24)并化简得
(27)
由于
(28)
将式(27)代入式(28)得
(29)
其中
(30)
于是,式(29)变化为
(31)
由于
(32)
对比式(31)和式(32)可得
(4LΔiq0)2=(-ψd0+Ψ)(3ψd0+Ψ)。
(33)
将式(33)变形可得
(34)
将式(34)代入式(27)可将转矩脉动抑制的相位条件转换为
θik=θek。
(35)
由于θek为k次谐波电动势相位,因此为抑制转矩脉动所需注入的谐波电流的相位角与对应次谐波电动势的相位角相同,即可以直接采用谐波电动势对注入电流进行定向。这为谐波电流指令的设计提供了条件,即若能够通过观测器获取谐波电动势及其相位,便可以获得注入谐波电流的相位。至于式(22)所示谐波电流幅值条件,则可依据转矩脉动幅值设计闭环控制系统自动生成,以克服参数影响。而转矩脉动的幅值在式(6)中已经分析,可以通过检测转速脉动获得,且可将速度脉动幅值与转矩脉动幅值间的比例关系融入到闭环调节器的系数中,实际实现时无需惯量等具体参数信息。这是本文的贡献,不仅从理论上计算了谐波电流的相位,而且该抑制方案具有较强的参数鲁棒性和实现的便捷性。
2 谐波电动势观测
由于在电机运行过程中谐波电动势不可测量,需要通过设计观测器进行估算。扩张状态观测器具有较强的参数鲁棒性和稳定性,且通过提升扩张状态的阶次能够提升其对快变信号的跟踪估算能力[30]。文献[35]对比研究了高增益观测器、扩张状态观测器和滑模观测器3种状态观测器的性能和特点。结果表明,扩张状态观测器在处理不确定性、干扰和传感器噪声等方面具有更好的效果。考虑到谐波电动势的快变特性、噪声敏感性等因素,本文采用ESO实现谐波电动势的观测。
本文测试所用电机转矩脉动主要为6次脉动,为了叙述方便,以下将采用6次脉动量为例进行分析与设计。
将式(7)和式(10)代入式(1)d轴电压方程,并将其改写为
(36)
将6次谐波电动势ed6扩张为一个新的状态变量γ,于是,状态扩张后的d轴状态方程可以表示为:
(37)
根据式(37)设计三阶扩张状态观测器为:
(38)
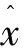
为分析所设计扩张状态观测器的稳定性,将式(38)减去式(37)得到d轴观测误差方程为:
(39)

可将式(39)所描述的状态方程的状态矩阵表示为
(40)
对应的特征多项式为
|sI-Ad|=s3-βd1s2+(6ωe)3s-
(41)
为获得较好的动态和稳态特性,可将特征根配置为同一负实数[37],即
|sI-Ad|=(s+p)3。
(42)
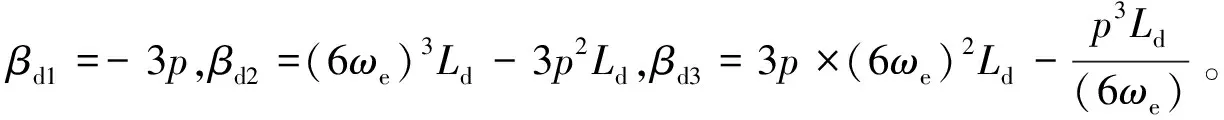
3 转矩脉动抑制方案设计
根据前文所述,转矩脉动的幅值大小可以用相同阶次的转速脉动幅值大小来体现,抑制转矩脉动相当于抑制同阶次转速脉动。因此,本文以6次转速脉动幅值作为反馈信号并通过调节器设计获取待注入谐波电流的幅值。
为提取6次转速脉动幅值,当获得转速信号ωm后,分别乘以6倍频的正弦量sin6θ和余弦量cos6θ并展开有:
ωmsin6θ=ωm0sin6θ-0.5ωm6sinφω6+
0.5ωm6sin(12θ+φω6);
(43)
ωmcos6θ=ωm0cos6θ+0.5ωm6cosφω6+
0.5ωm6cos(12θ+φω6)。
(44)
不难发现式(43)和式(44)中的直流量分别为-0.5ωm6sinφω6和0.5ωm6cosφω6。显然,若对乘积ωmsin6θ和ωmcos6θ进行低通滤波,便可获得对应的6次转速脉动信息,继而获得转速脉动幅值,即
(45)
据此,可将转速脉动幅值的提取计算过程表示为图2所示。
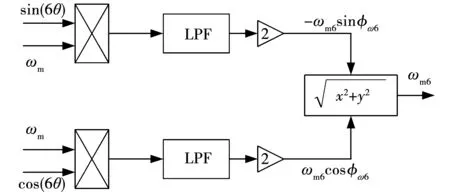
图2 6次速度脉动幅值计算Fig.2 Amplitude calculation of the 6th-order speed pulsation
由式(35)可知待补偿电流的相位与电动势对应次谐波相位相同,因此,谐波电流相位可表示为
(46)
依据图2所获得的转速脉动幅值设计闭环调节器获取待注入谐波电流的幅值,并依据式(46)计算谐波电流的相位,最终形成谐波电流指令。整体补偿电流指令的生成过程如图3所示,含转矩脉动补偿的PMSM矢量控制框图如图4所示。考虑到在新能源汽车、风力发电等领域电机驱动系统通常工作在转矩模式,通过电流指令的设定,间接实现转矩的跟踪控制。另外,考虑到电流控制是电机控制性能的关键,因此这里也仅对电流跟踪控制进行考察,电流指令人为地根据期望的转矩输出设定。同时考虑到转矩脉动抑制的需要,电流指令中会包含因转矩脉动抑制算法所生成的谐波电流,为了更好地对电流指令进行跟踪,这里电流调节器在PI基础上并联了用于谐波控制的旋转积分器。关于旋转积分器的设计,将在下一节进行讨论。

图3 转矩脉动抑制谐波电流指令生成Fig.3 Generation of the harmonic current reference for torque ripple suppression

图4 控制框图Fig.4 Block diagram of the control system
4 旋转积分器
由上一节的分析不难发现,为了抑制转矩脉动需要在定子电流中注入谐波。比如上一节以6次脉动为例,为对其进行抑制,需要在同步旋转坐标系下的定子电流指令中叠加6倍频基波频率的交流量。因此需要电流调节器具有对交流电流的跟踪能力。谐振控制器理论上能够实现谐振频率处增益无穷大,实现对谐振频率处交流量的无静差跟踪控制。理想谐振控制器的传递函数可表示为
(47)
其中:KR为谐振控制器系数;ωres为谐振角频率。然而,在对谐振调节器进行数字实现时会存在频率偏移现象,影响了实际控制效果[29]。
为克服这一问题,文献[36]针对并网逆变器交流电流的控制设计了比例双谐振控制器,实现了正、负序电流的无静差控制。双谐振控制器由两个旋转积分器构成,且旋转积分器直接在离散域进行设计,有效克服了数字化实现时离散化误差的影响[29]。在离散域中旋转积分器可表示为
C(n)=R(ωresτ)C(n-1)+hε(n)。
(48)
其中:h为采样周期;ε(n)=[εd(n)εq(n)]T为当前时刻输入信号;C(n-1)=[Cd(n-1)Cq(n-1)]T为上一时刻的输出;C(n)=[Cd(n)Cq(n)]T为当前时刻的输出;R(ωresτ)为旋转矩阵,有
(49)
为了说明其谐振特征,可将式(49)中的角频率ωres分别取正和负值可得:
(50)
将式(50)中的d轴分量进行整理得
(51)
其中:
将式(51)进行Z变换可得
(52)
由余弦函数的拉普拉斯变换可知,式(52)是连续域下谐振控制器的离散化形式[36]。图5是角频率分别为200、400、600、800、1 000 rad/s时的伯德图。

图5 双谐振控制器伯德图Fig.5 Bode diagram of dual resonant controller
5 实验研究
为对本文的分析和设计进行实验验证,搭建了2.2 kW永磁同步电机实验平台,如图6所示,其原理结构如图7所示。测试用永磁同步电机参数为Rs=2.62 Ω,Ld=72 mH,Lq=224 mH,ψd0=0.75 Wb,np=2,fn=50 Hz,In=4.0 A。负载电机采用台达伺服电机,稳态运行时没有明显的转矩脉动。伺服电机工作在速度控制模式,用于对机组转速进行闭环控制,而测试电机工作在电流跟踪模式,其指令电流依据设定转矩进行计算获得。控制器采用TI出品的DSP TMS320F28379D,逆变器主电路功率模块采用三菱PM100CL1A120,开关频率设定为9.6 kHz。测试电机驱动逆变器与负载电机伺服控制器采用共直流母线接线方式,母线电压由二极管整流电路提供,其大小为580 V。

图6 实验平台Fig.6 Picture of the test bench

图7 实验平台结构框图Fig.7 Schematic of test bench
图8和图9分别记录了50%负载转矩情况下电机运行于300 r/min和450 r/min时的实验结果。
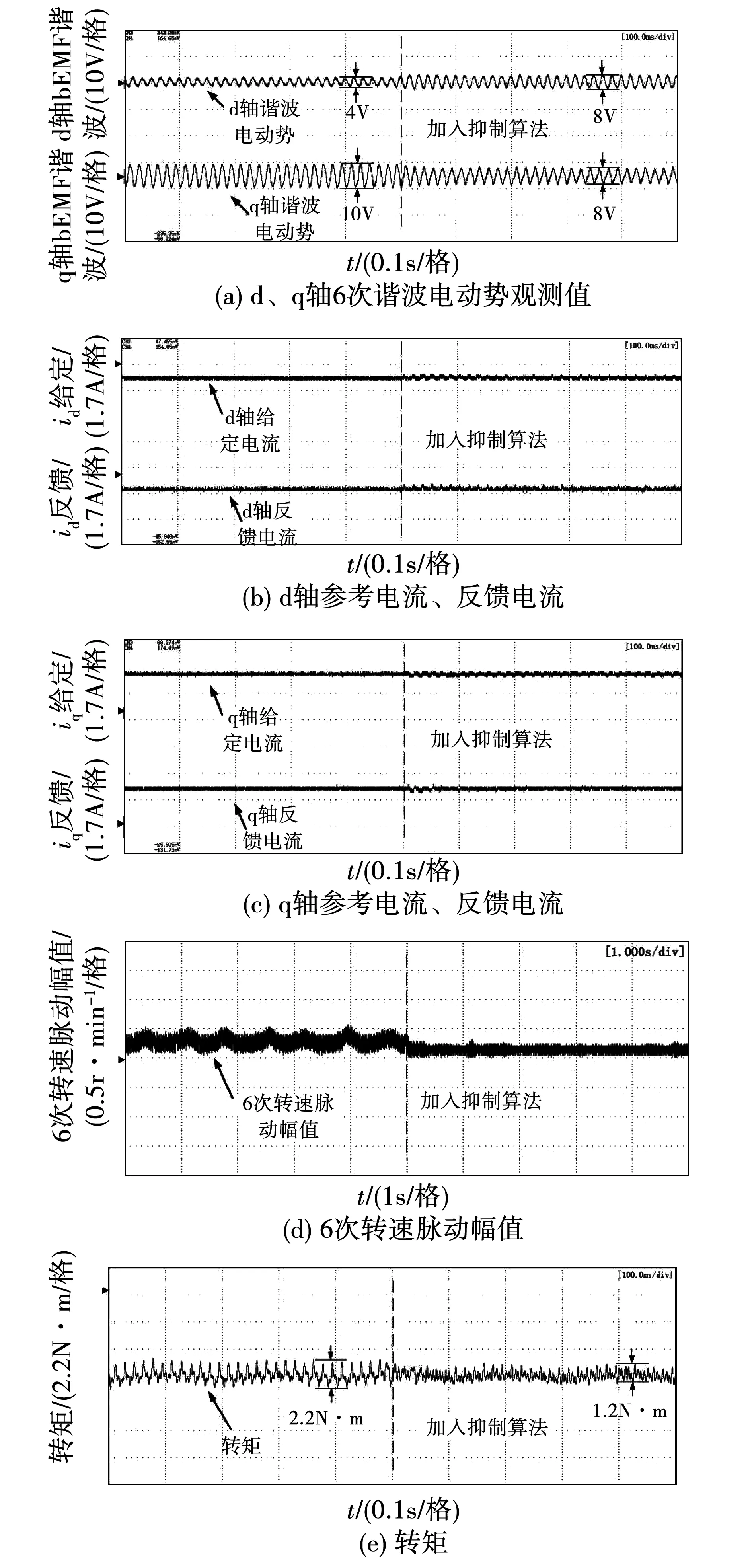
图8 300 r/min时半载下转矩脉动抑制Fig.8 Torque ripple suppression under half load at 300 r/min
图8(a)和图9(a)展示了所设计的扩张状态观测器在两种情况下均能实现对电动势谐波成分的较好观测。由于在实验中机组转速由负载电机进行控制,而测试电机仅工作在电流环模式,电流指令依据转矩输出设定。在加入转矩脉动抑制算法之前,电流指令为恒定值,因此电流中没有明显的谐波成分。加入转矩脉动抑制算法后,在电流指令中叠加了转矩脉动抑制算法所获得的用于转矩脉动抑制的谐波电流,在电流控制器(PI+旋转积分器)的作用下,定子电流中包含有谐波成分,如图8(b)、图8(c)和图9(b)、图9(c)所示。本文仅对转矩6次脉动进行抑制,对应的定子电流在同步旋转坐标系下,也表现出6倍基波频率脉动成分。通过图8(e)和图9(e)的转矩波形不难看出,在转矩脉动抑制算法启用之前,尽管电流中没有明显的谐波,但转矩中依然存在明显脉动。这是由定子电流基波与磁链(或电动势)谐波相互作用产生的,这也印证了单纯抑制定子电流谐波的方案难以消除转矩脉动。在没有启用抑制算法时,两种转速情况下转矩脉动峰峰值分别为2.2和2.4 N·m,转速越高,谐波磁链所产生的谐波电动势越大,在相同电流下所产生的转矩脉动也越大。启动转矩脉动抑制算法后,依据6次脉动成分,在同步旋转坐标系下的定子电流指令中注入6次电流脉动,在相位和幅值合适时,其与基波磁链的作用产生的转矩脉动量能够消除或减小转矩脉动。转矩的脉动也导致转速中存在明显的脉动,图8(d)和图9(d)中分别给出了对应转速下转速6次脉动量的幅值。显然,转矩的脉动导致了同频率的转速脉动。这为通过转速脉动提取转矩脉动信息提供了可能。另外,由于本文仅就6次脉动进行抑制,因此在启动脉动抑制算法后,转矩中依然含有一定的脉动,但转速的脉动得到了较好的抑制。实际上,考虑到算法执行时间、检测误差等因素,完全消除转矩脉动较为困难,通常算法都是将转矩脉动减小到可以接受的程度[17]。
类似地,在满载情况下电机分别运行于300和450 r/min时的实验结果如图10和图11所示。在加入转矩脉动抑制算法之前,随着基波电流的增加,基波电流与磁链谐波作用所产生的转矩脉动也将随着增加,如图10(e)和图11(e)所示。满载情况下,转矩脉动峰峰值分别为4和4.4 N·m。转矩脉动的增加也将导致转速脉动量的增加,如图10(d)和图11(d)所示。在脉动抑制算法启用之前,转速脉动的幅值分别为0.7和1.3 r/min。启用转矩脉动算法后,两种情况下的转矩脉动量分别降为2.3和2.4 N·m,相应地,转速6倍频脉动幅值分别降为0.3和0.4 r/min。

图9 450 r/min时半载下转矩脉动抑制Fig.9 Torque ripple suppression under half load at 450 r/min
为验证本文所提转矩脉动抑制算法在转速变化过程中的有效性,对转速变化过程进行了实验研究,如图12所示。

图10 300 r/min时满载下转矩脉动抑制Fig.10 Torque ripple suppression under full load at 300 r/min
实验过程中机组转速仍由作为负载电机的伺服系统控制,将机组转速由300 r/min上升到450 r/min。在此过程中,测试电机的转矩设定值保持不变,即电流的基波指令保持不变,注入的谐波指令由转矩脉动抑制算法自动生成。从图12(a)中可见,即便在加速过程中,观测器依然能够对磁链谐波进行较好的估计。图12(b)和图12(c)表明电流波形基本平稳,同时由于图中时间刻度较大,电流脉动不够明显,但从图12(d)和图12(e)所示的转矩和转速脉动情况下,即便在加速动态过程中,算法依然能够对转矩脉动进行较好的抑制。

图11 450 r/min时满载下转矩脉动抑制Fig.11 Torque ripple suppression under full load at 450 r/min

图12 满载下300 r/min匀加速至450 r/min转矩脉动抑制Fig.12 Torque ripple suppression from 300 r/min to 450 r/min underfull load
6 结 论
本文依据永磁同步电机电磁转矩数学模型,从谐波电动势和谐波电流的角度,理论上证明了为抑制转矩脉动所需注入的谐波电流与谐波电动势具有相同的相位,这为谐波电流的设计提供了理论基础。据此,论文设计了以转速脉动为反馈信息的直接谐波电动势定向转矩脉动抑制方案,并通过实验验证了方案对转矩脉动抑制的有效性。本文在理论推导和分析中忽略了不同次谐波电流之间的相互作用,这对抑制效果难免会产生一定的影响,但从实验效果看,依然能够将转矩脉动抑制到可以接受的程度。关于考虑谐波间的相互影响以及谐波电流的注入与损耗关系的量化运算还有待进一步研究。

