基于改进有源阻尼的柔性关节机械臂伺服系统振动抑制策略

刘铠源， 杨明

(哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001)

0 引 言

近些年，随着智能制造2025计划的提出，工业机器人已广泛应用于各大工业领域，如何提高工业机器人的末端轨迹精度是如今研究的热点与难点。RV减速器，皮带轮等工业机器人的核心部件不可避免地存在柔性，随着伺服驱动器控制带宽不断提高，柔性关节的存在会在机器人刚性运动过程中引起末端抖动的问题，在如工业焊接、航空航天等高精度应用领域，末端抖动会大幅降低生产效率，甚至引起严重事故。因此研究工业机器人抖动抑制算法具有重要意义[1-2]。

针对工业机器人中柔性关节引起的末端抖动，现有抑制算法主要包括机械法，轨迹规划与输入整形法，滤波器法，状态反馈法以及有源阻尼等方法。

机械法是通过优化减速器及联轴器等连接部件的刚度抑制振动，但增加了系统的成本以及研发周期。轨迹规划法针对位置指令高阶不连续可导而激发出的末端衰减振动问题，通过对位置指令平滑处理，实现末端抖动的抑制，常见的轨迹主要有七段S曲线指令，正余弦加加速度指令等[3]。输入整形算法通过将输入信号和一系列脉冲信号进行卷积，实现末端抖动的抑制。但文献[4]指出由于输入整形器的特性，当往复运动周期较短时，将引起运动指令变形，甚至导致运行轨迹不平滑，因此该方法还有待改进。

滤波器法如陷波滤波器，通常在含有弹性连接装置的数控系统中广泛使用，以解决高频的机械谐振问题，但此算法严重依赖谐振频率的准确辨识[5]，由于工业机器人中各伺服电机负载惯量时刻改变，难以实时准确辨识各轴的机械谐振频率，且工业机器人中末端的振动频率较低，因此陷波滤波器在工业机器人的应用还有待改进。状态反馈法通过对一些状态变量如轴转矩[6]，负载位置转速等增加末端传感器或采用观测器的方法进行观测与补偿，但增加了系统成本或算法的复杂度。

针对以上问题，文献[7]提出一种有源阻尼策略，对电机侧的转速反馈增加虚拟阻尼，补偿至电流指令处，实现振动的抑制。文献[8]将传统有源阻尼的补偿量改进为转速反馈的微分，解决了油井钻井平台中存在的抖动问题，但其仍存在动态响应速度变慢的问题。为此，本文提出一种改进有源阻尼策略，首先基于理想转速指令获取转速反馈中的振动分量，为了避免对转速反馈中振动频率之外的有效频率分量过补偿，采用峰值滤波器实现对振动频率的准确观测，最终将结果前馈至电流指令处，实现工业机器人末端抖动抑制与动态响应速度的兼顾。同时，采用相位超前环节实现对补偿电流相位的控制，提高算法的鲁棒性。最后通过一台8 kg六轴工业机器人进行算法的验证。

1 柔性关节机械臂抖动机理

工业机器人中存在的减速器，传动带等弹性部件会引起运动过程中的抖动问题，为分析其抖动机理，将含有柔性关节的机械臂系统等效为双惯量弹性模型，如图1所示。

图1 柔性关节双惯量机械传动装置模型Fig.1 Model of flexible joint two-inertia mechanical transmission device

图中柔性传动部件等效为扭转弹簧，电机与负载分别等效为两个惯量，系统的动力学方程为：

(1)

其中：J1、J2分别为电机与负载侧的转动惯量；K为弹性轴的弹性系数；Te、T1、Tω分别为电磁转矩；负载转矩及轴转矩；ω1、ω2分别电机与负载侧转速；θ1与θ2分别为电机与负载侧位置反馈。由式(1)可得转速反馈与电磁转矩之间的传递函数为

(2)

式(2)表明柔性关节会为系统引入一对共轭零点fARF与共轭极点fNTF，其表达式分别为：

(3)

式(2)对应的Bode图如图2所示。由于谐振峰值的存在，随着控制系统带宽的不断提高，系统运行时将引起振动问题，严重降低系统轨迹跟踪精度。同样的结论可以由轴转矩Tω的表达式得到，即

(4)

式(4)为临界阻尼状态的二阶系统，当转矩Te发生变化时，轴转矩上激发出的持续振动，会导致电机速度的波动，最终体现为机器人末端的抖动问题。

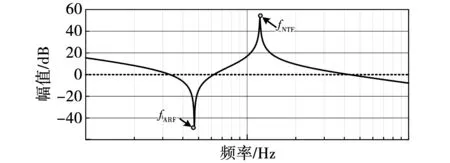
图2 双惯量弹性系统Bode图Fig.2 Bode diagram of two-inertia elastic system

2 有源阻尼抑振机理

J1sω1=Ktiqref-Tω-Baω1。

(5)

根据式(1)与式(5)得到电机侧转速与速度控制器输出等效的电磁转矩之间的表达式为

(6)

图3 不同有源阻尼控制框图Fig.3 Control block diagram of different active damping structures

补偿前后转速与速度控制器输出等效的电磁转矩之间的传递函数式(2)与式(6)下的极点图如图4所示。结果表明随着有源阻尼的引入，系统的极点由虚轴上的一对共轭极点与原点处的极点，移动至左半复平面上，振动分量得以快速衰减。

图4 有源阻尼对系统极点的影响Fig.4 Influence of active damping on the poles of the system

构建小信号增量法进一步分析，在振动状态下，将各转矩，转速近似为以谐振频率正弦规律波动的小信号，系统在振动频率下的矢量图如图5所示。其中：Δω1为电机侧转速反馈中的振动分量；ΔTePI为速度控制器输出电流指令对应的转矩；ΔTe为补偿有源阻尼后的实际电磁转矩振动分量。为简化分析，以速度控制为例，即转速指令中的振动分量为零，转速误差为-Δω1，由于速度控制器采用比例积分控制，ΔTePI滞后于转速误差-Δω1角度θASR，如图5中虚线所示，其中θASR由速度控制器的参数所决定。

图5 有源阻尼抑振机理矢量图Fig.5 Vector diagram of the vibration suppression mechanism by active damping

为ΔTePI补偿有源阻尼分量-BaΔω1后，实际电磁转矩分量为

ΔTe=ΔTePI-BaΔω1。

(7)

如图5中实线所示，实际电磁转矩ΔTe滞后轴转矩角度ΔTω的角度为φ，因此，电磁转矩ΔTe可以分解为一个滞后于轴转矩90°的垂直分量ΔTe⊥及与轴转矩平行分量ΔTep，如图5中点划线所示，其中：

(8)

式中k1和k2为中间变量，其大小为：

(9)

由式(4)所示轴转矩公式，其增量频率特性为

(J1J2(jω)2+K(J1+J2))ΔTω=

K(J2ΔTe+J1ΔT1)。

(10)

其中ΔT1为负载转矩分量，于是有

(J1J2(jω)2+K(J1+J2))ΔTω=

K(J2ΔTe⊥+J2ΔTep+J1ΔT1)。

(11)

将式(8)代入式(11)得到

(J1J2(jω)2+K(J1+J2))ΔTω=

KJ2(-jωk1ΔTω+k2ΔTω)+KJ1ΔT1。

(12)

进一步推导得到

(J1J2(jω)2+KJ2jωk1+K(J1+J2)-

k2KJ2)ΔTω=KJ1ΔT1。

(13)

由式(13)可得，有源阻尼策略通过为系统增加含有jω的阻尼项，系统由式(10)所示的临界稳定状态恢复为欠阻尼的状态，实现对振动的抑制。

3 改进有源阻尼策略

3.1 改进有源阻尼结构

采用图3(b)所示的结合高通滤波器的有源阻尼策略可以一定程度改善传统有源阻尼响应速度变慢的问题，其中高通滤波器采用一阶高通滤波器，其传递函数为

(14)

高通滤波器能够滤除转速反馈低频段的有效频率，避免低频段等效阻尼的过度补偿，但由于转速反馈的中高频率分量通过高通滤波器并无明显衰减，此部分分量仍然存在过度补偿阻尼的问题。

因此，本文提出了图3(c)所示的改进有源阻尼策略，首先对理想转速指令与转速反馈作差，实现转速反馈中有效频率分量的初步滤除。获取理想转速指令时，由于运动控制器只能发送以脉冲为单位的整数值，直接对位置指令差分，将存在位置量化误差引起的高频周期性噪声，针对此问题，本文对位置指令不完全微分，即在转速差分后，通过低通滤波器对高频的噪声滤波，实现理想转速指令的获取，降低系统噪声。

其次，采用峰值滤波器进一步提取转速反馈中的振动分量。峰值滤波器为一种特殊的带通滤波器，其传递函数为

(15)

峰值滤波器Bode图如图6中实线所示。结果表明，通过预先配置峰值滤波器的中心频率为实际振动频率，可以实现中心频率处振动分量的观测，同时调节滤波器通带宽度，能够提高系统的鲁棒性。

图6 峰值滤波器与相位超前环节Bode图Fig.6 Bode of the peak filter and lead compensator

由于工业机器人电机侧与末端负载侧之间存在柔性关节与柔性连杆，两侧的转速存在一定的相位差，前述改进有源阻尼算法是基于电机侧转速反馈信息进行补偿，相位差的存在会一定程度影响末端的振动抑制效果。而一方面由于机器人位姿时变，机械分析相位关系较为复杂，另一方面，为了降低成本，工业机器人末端并不常配有传感器，电机侧与负载侧之间的相位差获取困难，为了使算法适用于此类工况，本文提出对转速反馈选频得到的低频振动信号，通过相位超前环节Glead(s)，实现对补偿电流相位的调整，相位超前环节传递函数为

(16)

其Bode图如图6中点划线所示，结果表明，相位超前环节能够在中心频率附近提供一个超前的相角，从而实现对补偿电流相位的控制，由于通常电机侧与负载侧的相位关系分析较复杂，因此相位超前环节参数的配置需离线根据实际抖动抑制效果调试出鲁棒性较好的参数，以适用于工况复杂的工业机器人应用。

3.2 改进有源阻尼与传统有源阻尼对比分析

为了对比改进有源阻尼相比于传统有源阻尼与高通有源阻尼的特点，绘制3种有源阻尼结构转速反馈到补偿电流处的传递函数对应的Bode图如图7所示。

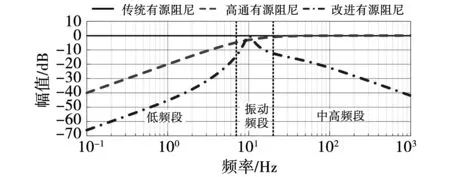
图7 3种结构转速反馈与补偿电流间传递函数Bode图Fig.7 Bode of transfer function between speed feedback and compensation current of three structures

图中，3种有源阻尼结构均能够使转速反馈中的振动频率分量以较低的衰减通过，并补偿到电流指令中，实现末端抖动的抑制。而传统有源阻尼无法滤除低频与中高频段的有效频率分量，产生过补偿问题。高通有源阻尼虽然解决了转速反馈低频段有效频率分量过补偿的问题，但中高频段并无改善。而图中改进有源阻尼策略通过采用峰值滤波器，能够实现对振动分量提取的同时，有效抑制其他有效频率段，解决了过补偿问题。

由于图3中改进有源阻尼的理想转速指令部分相当于一种速度前馈，其有利于系统动态响应性能，为简化分析，仅考虑峰值滤波器的作用。本节主要分析改进有源阻尼与两种其他有源阻尼结构对系统动态响应性能影响的差异，首先推导3种结构的速度开环传递函数。图3中3种阻尼结构的速度控制器为

(17)

其中:Ksp、Ksi分别为速度控制器的比例系数和积分系数。电流环作为系统的最内环，其带宽远高于外环，将电流环的闭环传递函数Gcc(s)简化为1分析。于是有传统有源阻尼、高通滤波器有源阻尼以及简化后的改进有源阻尼的速度开环传递函数分别为：

(18)

当位置控制器GP(s)采用比例控制，比例系数为Kpp，则三者的位置开环传递函数可以分别表示为：

(19)

根据式(19)可以绘制出3种采用不同有源阻尼策略的位置开环传递函数Bode图如图8所示，其中参数按照表1进行配置。

图8 不同阻尼结构位置开环传递函数Bode图Fig.8 Bode diagram of position open-loop transfer function under different damping structures

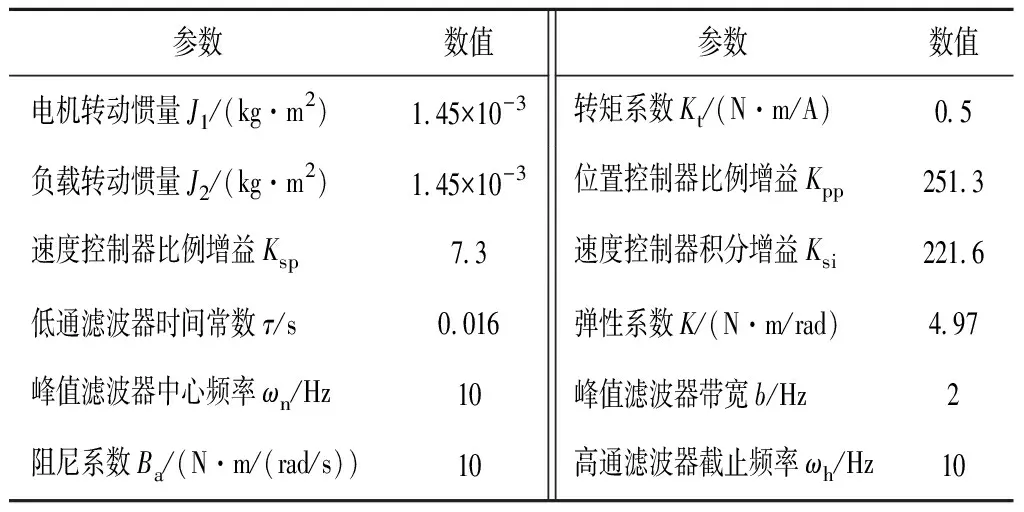
表1 仿真参数

图8的Bode图结果表明，在共有参数均一致的情况下，改进有源阻尼结构的幅频曲线在中高频段与未补偿的原始结构最为接近，未补偿下位置开环截止频率为44 Hz，而传统有源阻尼，高通有源阻尼及改进有源阻尼的位置开环截止频率分别为20、22以及41 Hz，证明了改进有源阻尼在3种阻尼结构中位置开环截止频率最高，同时改进结构相位裕度最高为87.5度，其稳定性最强。

根据式(19)可以得到3种控制结构的位置闭环传递函数为：

(20)

由式(20)可以绘制出3种阻尼结构位置闭环传递函数的Bode图如图9所示。

图9 不同阻尼结构位置闭环传递函数Bode图Fig.9 Bode diagram of position closed-loop transfer function under different damping structures

图9的Bode图表明，改进有源阻尼结构的位置环带宽在3种阻尼结构中最高为44 Hz，且最接近未补偿的55 Hz。上述分析证明了改进有源阻尼通过采用峰值滤波器，避免对有效频率分量的过补偿，解决了两种传统阻尼结构动态响应性能变差的问题。

为了验证算法的有效性，根据表1中的参数仿真分析，令位置指令为峰值0.01 rad，频率55 Hz的正弦曲线，分别测试无阻尼结构，及不同有源阻尼结构下位置响应情况，仿真结果如图10所示。

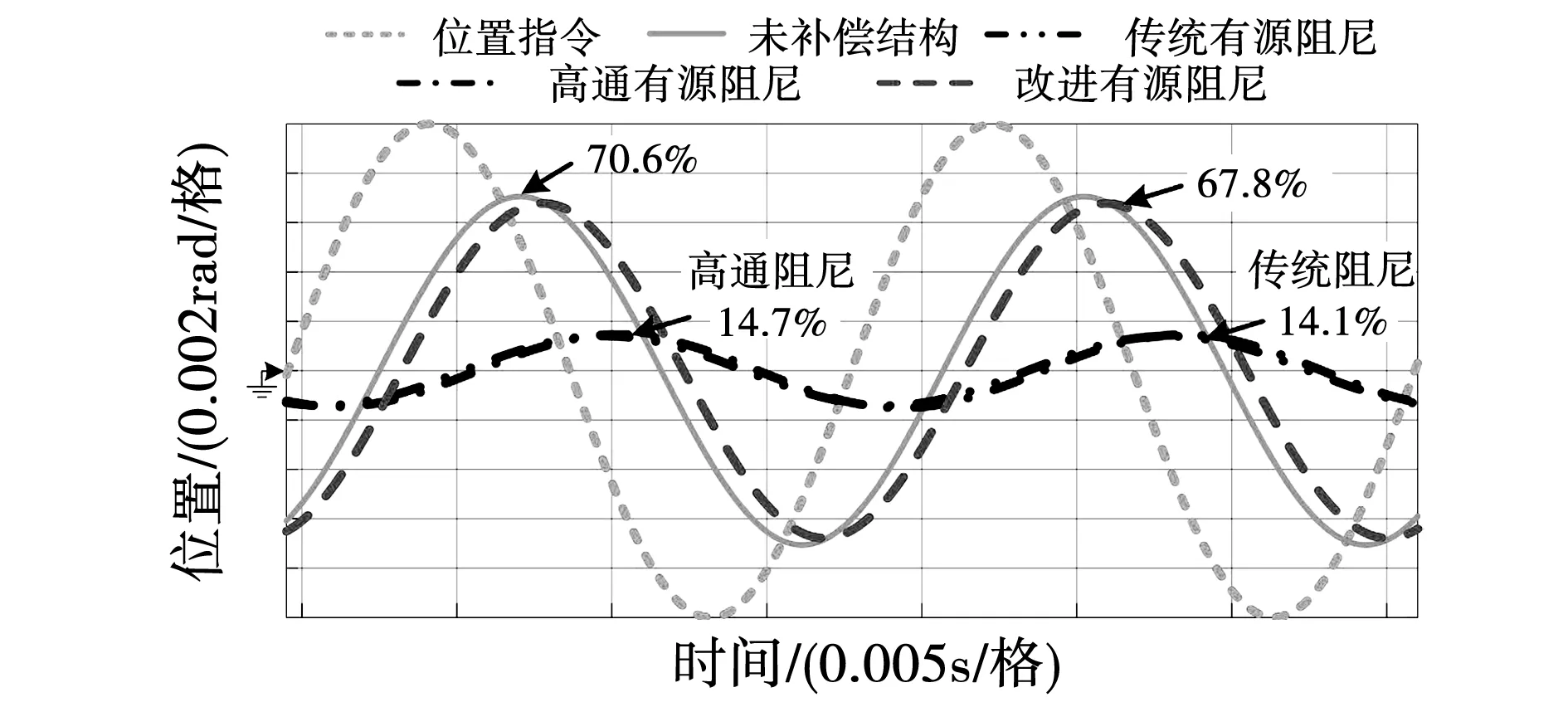
图10 不同阻尼结构正弦指令仿真结果Fig.10 Simulation results of sinusoidal reference under different damping structures

仿真结果表明，未加入有源阻尼结构时，位置反馈存在70.6%的衰减，与图9所示-3 dB处的带宽基本一致。而采用传统有源阻尼与高通滤波器有源阻尼下的位置反馈分别衰减到原来的14.1%和14.7%，严重降低了原有系统的位置环带宽。而随着改进有源阻尼结构的引入，位置反馈仅衰减到原来的67.8%，同时位置反馈的相位滞后也最接近于原有结构，上述仿真结果证明了改进有源阻尼有效解决了两种传统阻尼降低系统动态响应性能的问题。

4 实验结果

为验证所提算法的有效性，本文采用一台8 kg六轴工业机器人RB08A3进行实验验证，其中系统的位置指令来自于运动控制器GL100与示教盒，实验平台如图11所示。

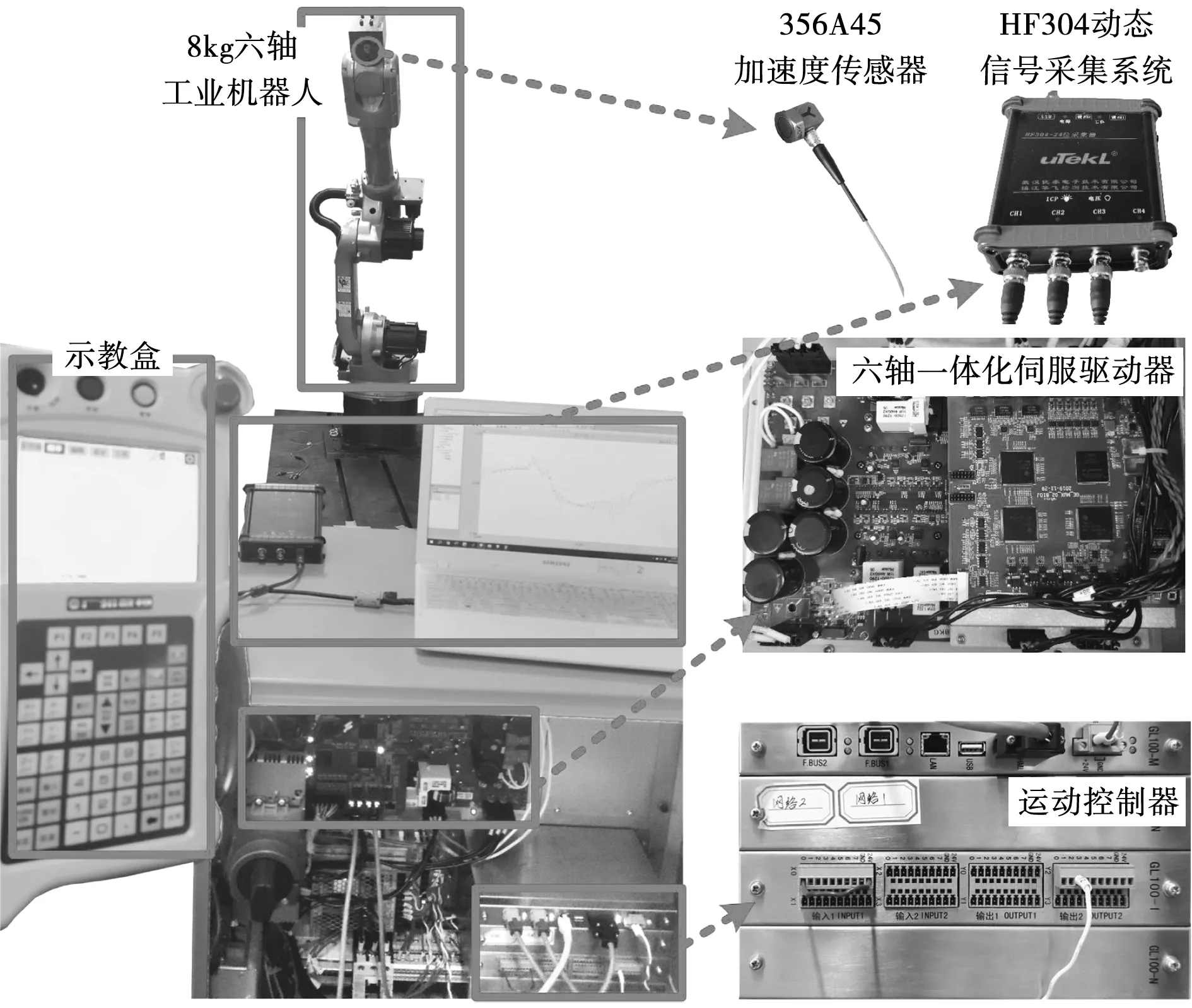
图11 实验平台Fig.11 Experiment platform

工业机器人应用中末端振动抑制更重要，本文将一枚磁吸式加速度传感器356A45吸附在工业机器人末端负载运动方向的切向上，并采用优泰HF304动态信号采集系统实时获取末端振动加速度。机器人运动过程中的抖动主要来自于二轴和三轴，本文以二轴电机为例进行实验，为避免其他轴姿态变化影响，其他轴定位在如图12(a)所示的固定位置。被测工业机器人二轴电机参数如表2所示。

表2 电机参数

图12 被测8 kg工业机器人两种工作姿态Fig.12 Two working postures of the tested 8 kgindustrial robot

理想转速指令获取实验如图13所示。对位置指令进行差分得到的转速指令如虚线所示，其中存在高频噪声信号，波动的幅值达到了3.5 r/min，不能直接应用于改进有源阻尼中。采用不完全微分后的速度指令如图13中实线所示，其有效抑制了微分引起的高频噪声。

工业机器人保持图12(a)所示的伸直状态，二轴电机做往复周期运动，匀速段速度为750 r/min的末端振动加速度时域与频域实验结果如图14所示，其中峰值滤波器和相位超前环节的中心频率设置为10 Hz，带宽设置为2 Hz，相位超前系数为3，阻尼系数设置为0.1 N·m/(rad/s)。

实验结果表明，无有源阻尼结构在8.9 Hz处存在振动峰值，当加入改进有源阻尼结构后，末端振动在8.9 Hz处的主峰由0.087 g降低到了0.043 g，降低了原来的50.6%，证明了算法的有效性。

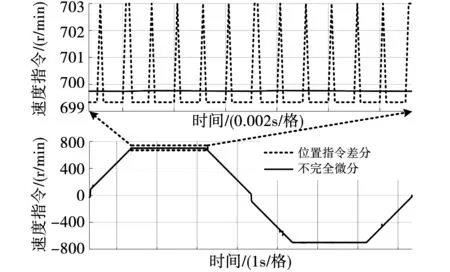
图13 理想转速获取结果Fig.13 Results of ideal speed

图14 伸直状态750 r/min下改进有源阻尼抑振结果Fig.14 Improved active damping vibration suppressionresults at straightened condition under750 r/min

上述参数在伸直状态转速750 r/min下具有较好的抖动抑制效果，但由于通常工业机器人各轴的负载以及位姿时变，因此寻找一套各类工况下普适性较好的参数十分重要。

实验中通过调试，被测电机在峰值滤波器中心频率ωn为9 Hz，带宽b为14 Hz，相位超前环节超前系数α为4，中心频率ωc为8 Hz，阻尼系数Ba为0.04，低通时间常数τ为0.016 s，算法鲁棒性较强。为验证算法鲁棒性，仍保持机器人处于伸直状态，图15为二轴电机以1 500 r/min往复运动的实验结果。

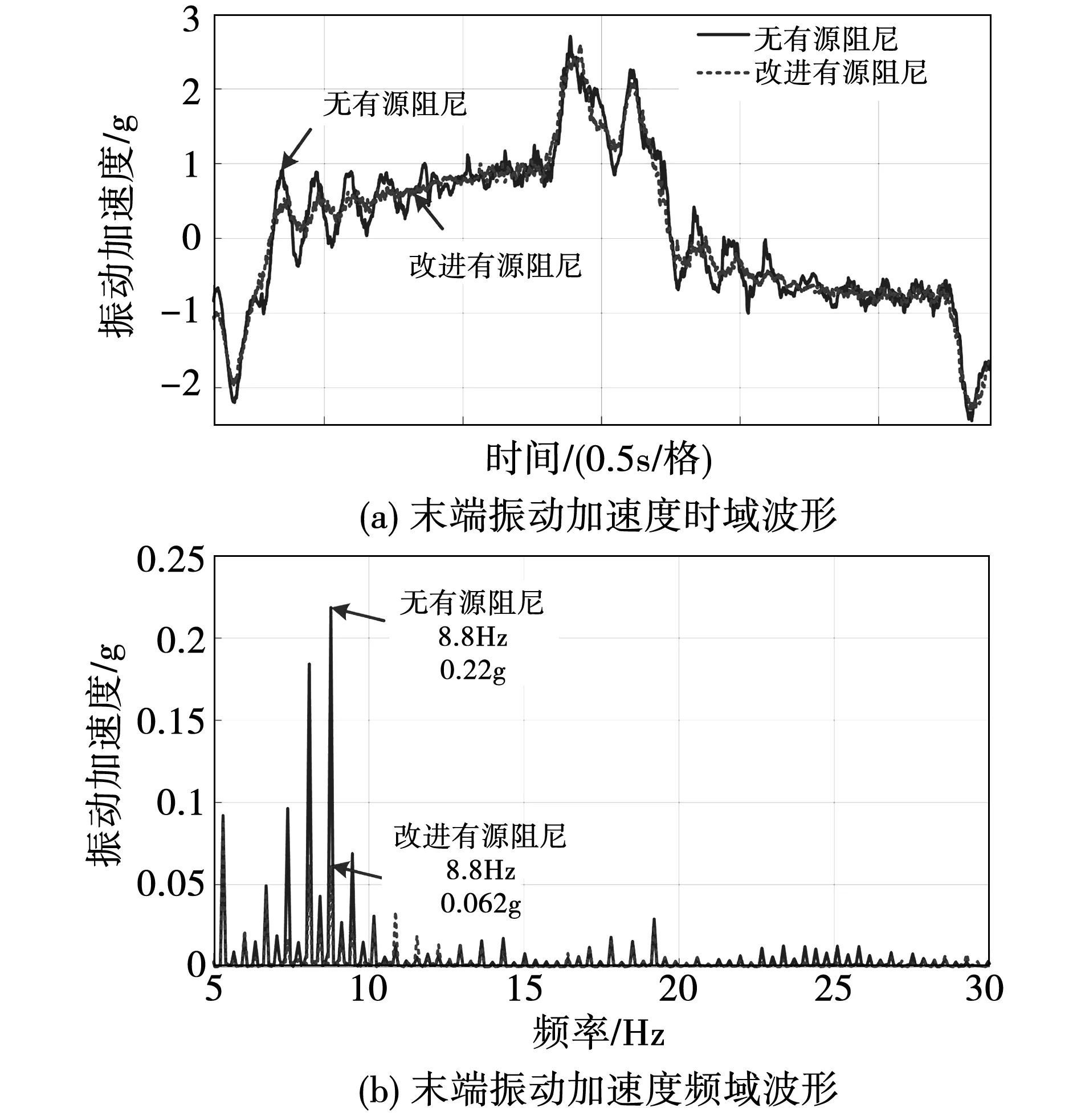
图15 伸直状态1 500 r/min下改进有源阻尼抑振结果Fig.15 Improved active damping vibration suppressionresults at straightened condition under 1 500 r/min

结果表明，在8.8 Hz处的主峰由0.22 g降低到了0.062 g，末端振动时域波形表明，在全过程末端的振动均有较好的抑制效果。

令机器人三轴旋转90°，并保持恒定，如图12(b)所示，同样令机器人二轴做速度为1 500 r/min的周期往复运动，图16所示的实验结果表明，在90度位姿下，末端的振动幅值由0.096 g降低到了0.055 g，降低了42.7%，证明了算法的鲁棒性。

为进一步验证算法的有效性，将机器人伸直状态及90°位姿状态，不同转速及阻尼系数时，末端振动加速度最大振动幅值汇总如图17所示。

结果表明，阻尼系数设置为0.04时，末端振动抑制效果较好，在较高的转速下，效果更加明显，虽然在不同的转速下，系统的振动频率有一定改变，但是将峰值滤波器的中心频率设置为9 Hz，且所有参数均保持恒定的情况下，末端的振动幅值平均能够降低原来的32%左右，证明了算法的有效性与鲁棒性。

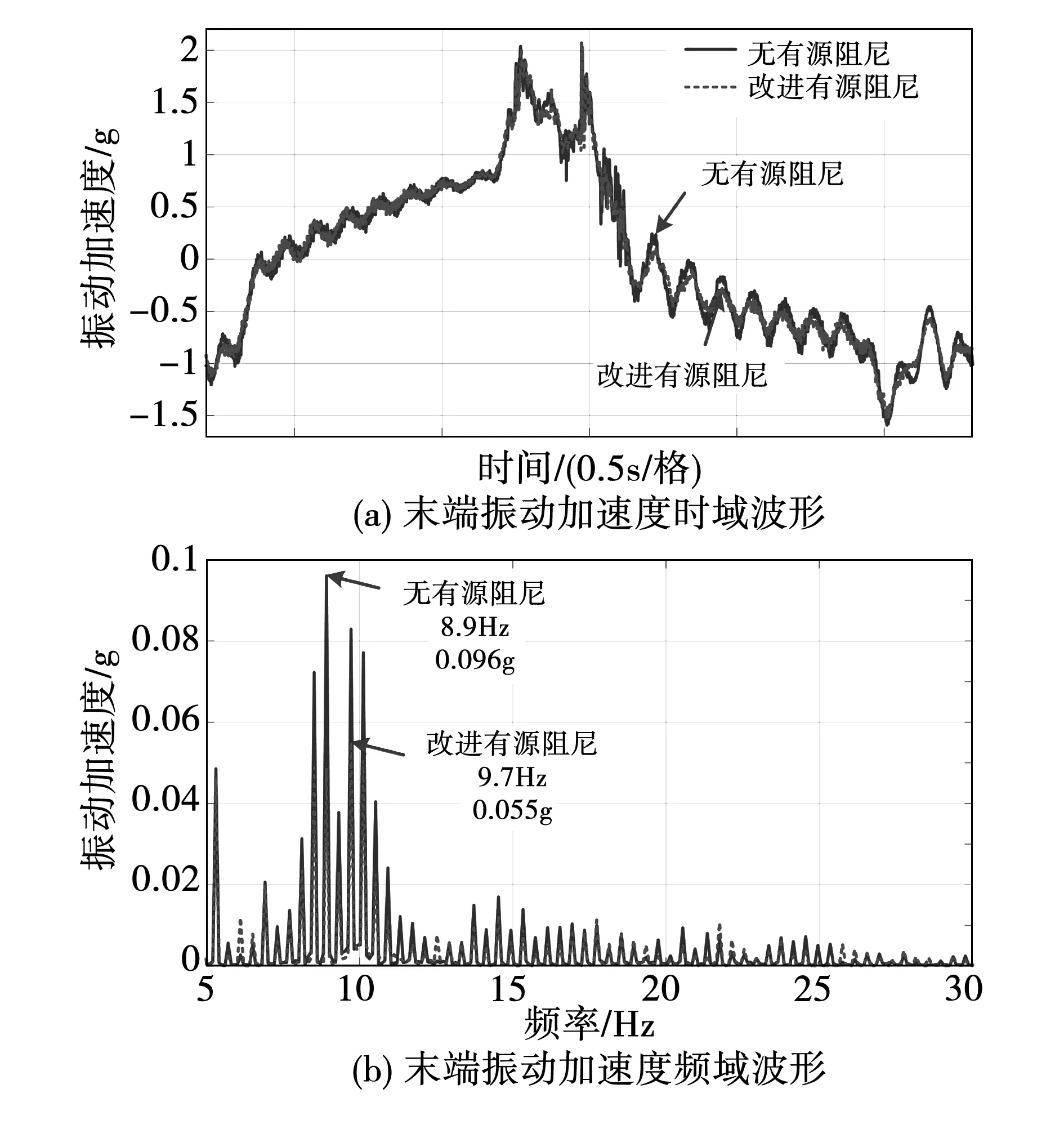
图16 90°状态1 500 r/min下改进有源阻尼抑振结果Fig.16 Improved active damping vibration suppression results at 90 degrees condition under 1 500 r/min

图17 不同工况末端振动加速度FFT最大幅值Fig.17 FFT maximum acceleration vibration amplitude under different working conditions

5 结 论

针对含有减速器等柔性连接部件的工业机器人运动过程存在末端抖动问题，本文提出一种改进有源阻尼抖动抑制策略，分别通过对理想转速指令与转速反馈作差以及引入峰值滤波器的方式，实现对低频振动的准确观测，相比于传统有源阻尼及结合高通滤波器的有源阻尼策略，所提算法由于避免对有效频率过补偿，能够兼顾末端抖动抑制能力与动态响应性能。此外通过引入相位超前环节调整补偿电流的相位，实现末端抖动的进一步抑制。所提算法结构简单，适用于工业机器人伺服系统无法实时获取末端振动信息的工况，降低了机器人系统的成本。最后8 kg六轴工业机器人的实验结果证明了所提算法能够将工业机器人末端振动幅值平均降低原来的32%左右。