基于电磁仿真的铁磁共振线宽测试研究

方清宇，张方远，吴 琼，葛洪良

(1. 中国计量大学计量测试工程学院，浙江 杭州 310018; 2. 东阳富仕特磁业有限公司，浙江 东阳 322105)

0 引 言

微波铁氧体材料自二十世纪中叶被发现以来，一直为科研人员所重视。因其具有旋磁性(即在稳恒磁场和微波磁场的共同作用下材料所显示出来的磁导率的张量特性和铁磁共振特性)[1]，微波铁氧体材料被广泛地使用在通信、电视、雷达、人造卫星、导弹系统、电子对抗系统及高能粒子加速器等民用和军用的各个方面[2]。为适应目前5G通信技术的发展，微波铁氧体材料需要具备较小的电磁损耗（减少发热，确保仪器在高功率下稳定运行）[3]。由于微波铁氧体材料的微波磁损耗与共振线宽密切相关，所以测量其共振线宽成为了微波铁氧体研发一项重要的工作。

国际上一直高度重视铁磁共振线宽测量方法的研究和标准的制定。1958年，E.G.Spencer和R.C.Lecraw首次使用矩形谐振腔微扰理论来测试单晶钇铁石榴石(YIG)材料的铁磁共振线宽[4-5]，解决了铁磁共振线宽测量的难题。国家标准GB/T 9633—2012《微波频率应用的旋磁材料性能测量方法》[6]采用了1982至2011年版本的国际电工委员会IEC60556“微波铁氧体材料参数测量标准”[7]文件中推荐的基于谐振腔微扰理论的铁磁共振线宽测试方法。这些文件均对铁磁共振线宽的测量原理和方法著有详细地介绍。本文的部分理论分析和测量方法都是根据国标实施的。

根据谐振腔微扰法的测量原理[8]，本文采用电磁仿真软件HFSS搭建了铁磁共振线宽测量的模拟系统[9-10]，HFSS（High Frequency Simulator Structure）是原美国Ansoft公司开发有限元法的三维结构电磁场仿真软件，具有精确自适应的场解器、功能强大的电性能分析能力后处理器，能计算任意形状三维无源结构的S参数和全波电磁场。由Ansoft HFSS和Ansoft Designer构成的Ansoft高频解决方案，是目前唯一以物理原型为基础的高频设计解决方案，提供了从系统到电路直至部件级的快速而精确的设计手段，覆盖了高频设计的所有环节。目前谐振腔微扰法已经十分成熟，但仍有很多值得探究的问题。本文基于微波铁氧体的铁磁共振线宽对其材料结构敏感的原理，研究了样品尺寸对共振线宽测量结果的影响，并且探究了样品尺寸满足微扰理论的条件，提出了一种根据谐振曲线判断样品是否满足微扰理论的方法。

1 测量原理

1.1 测量模型

谐振腔微扰法测量铁磁共振线宽的模型如图1所示。采用BJ100型（国际标号为WR90）矩形波导，可以在8.2～12.5 GHz下进行测量。腔壁为理想导体，两侧放置中央开孔的铜板，腔内介质为空气。谐振腔与微波波导的耦合方式为小孔耦合[11]。a=22.86 mm为谐振腔的宽度，b=10.16 mm为谐振腔的高度，L为腔长，不同的腔长可以将谐振腔调整到不同的谐振模式[12]。

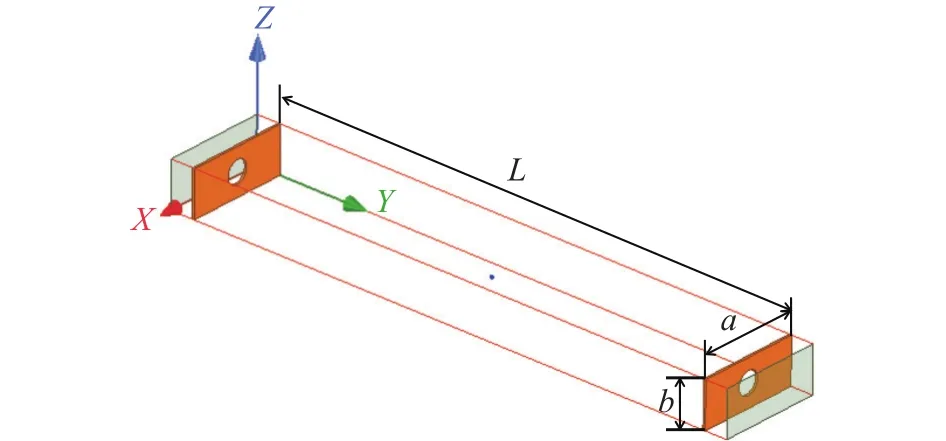
图1 铁磁共振线宽测量模型

1.2 谐振腔微扰理论

当微波铁氧体材料在谐振腔中时，要研究其对谐振腔电、磁性质的影响，需要解带有边界关系的麦克斯韦方程。但由于介质的各向异性，我们只能对少数形状简单且腔壁为理想导体的谐振腔进行精确求解。在实际情况中，金属的电导率是有限的，会使边界条件复杂化。所以一般采用微扰理论这种近似的方法来进行求解。

微扰法是指将足够小的样品置于谐振腔中，将样品放入前的谐振腔视为未扰动状态，将样品放入后的谐振腔视为扰动状态，则除样品所在处外，其余位置的电磁场相差很小，且谐振腔的谐振频率在样品放入前后变化无几。所以经常用未扰动状态的解来近似扰动状态的解。

假设V0为谐振腔的内体积，V1为微波铁氧体样品的体积，ω0和ω为未扰动与扰动状态下谐振腔的谐振频率，ε0和 μ0为未扰动状态下腔内介质的介电常数和磁导率，ε和 μ为扰动状态下腔内介质的介电常数和磁导率，Δ μ=μ-1，Δ ε=ε-1。未扰动时的交变电、磁场为E0、H0，扰动时的交变电磁场为E、H。则可以由麦克斯韦方程推导出谐振腔微扰理论的基本公式[13]：

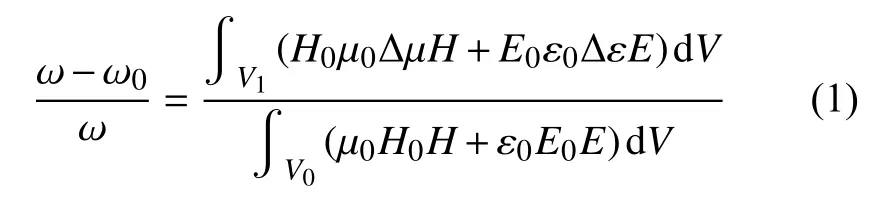
由于样品体积很小，放入前后对腔内场的影响可以忽略不计。所以，尽管样品内外的电磁场不同，但仍可以用样品外的电磁场近似样品内的电磁场，式(1)可化为：

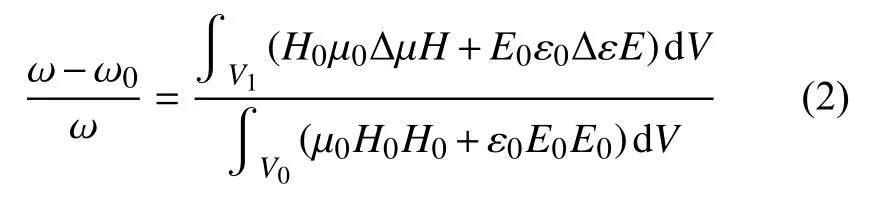
测量时需采用小球样品，将其放置在腔体中磁场最大，电场最小的地方，具体位置可以根据谐振腔的谐振模式来确定。

2 铁磁共振线宽测试

微波铁氧体材料的共振线宽是结构敏感量，在受到结构因素的影响时会有较大波动[14]。本文基于电磁仿真软件，在规定样品的铁磁共振线宽ΔH为50 Oe的情况下，研究了样品的尺寸对测量结果的影响

2.1 不同直径样品的铁磁共振线宽

在本文中，谐振腔的谐振模式为TE106，腔体内部的场分布如图2所示。根据要求，可将样品小球放于腔体中心位置，此处位于电场边缘，且有两个磁场叠加，是腔内电场最小，磁场最大的地方。

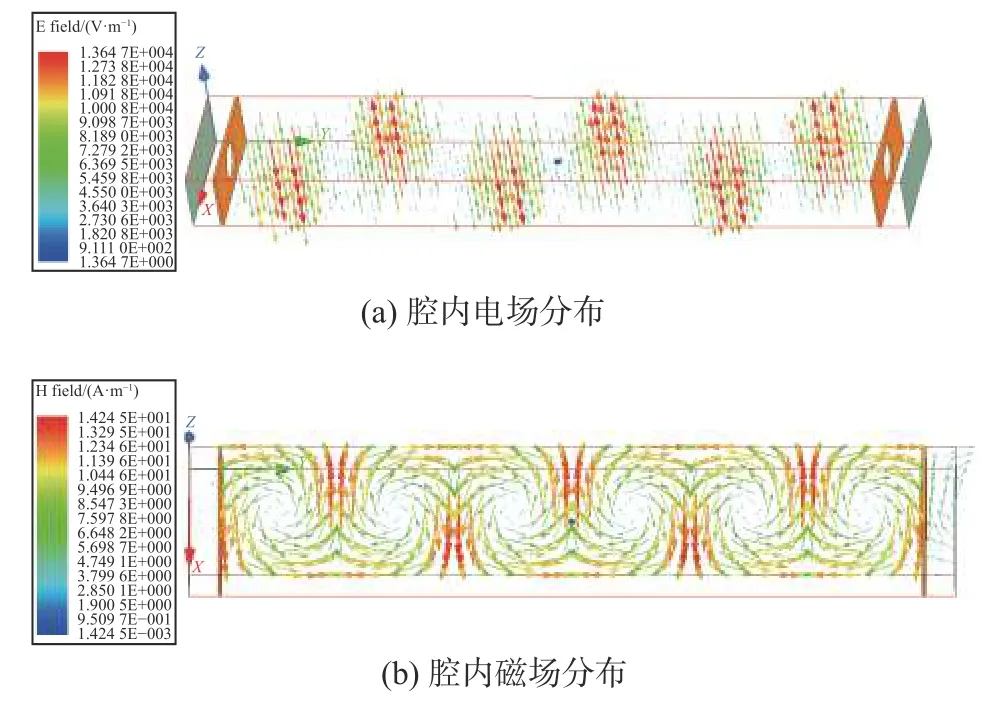
图2 谐振腔内的电磁场分布

在铁磁共振线宽的仿真测试中，一般采用S参数来表征测试样品的功率特性（S参数即散射参数，是微波传输中的一个重要参数，描述了传输通道的频域特性，通过S参数可以看到传输通道的很多特性）。其中的S21表示通道内正向传输的增益，可以反映样品吸收功率的大小。

以下为铁磁共振线宽的测量步骤：

1）将偏置磁场的值设为0，即在没有偏置磁场的情况下求解出谐振腔的谐振曲线，得到图3中S21(0)的值。2）调整偏置磁场值，找到使样品吸收功率最大的偏置磁场值H3，求解此时谐振腔的谐振曲线，得到图3中S21(3)的值，样品的吸收功率与偏置磁场值的关系如图4所示。

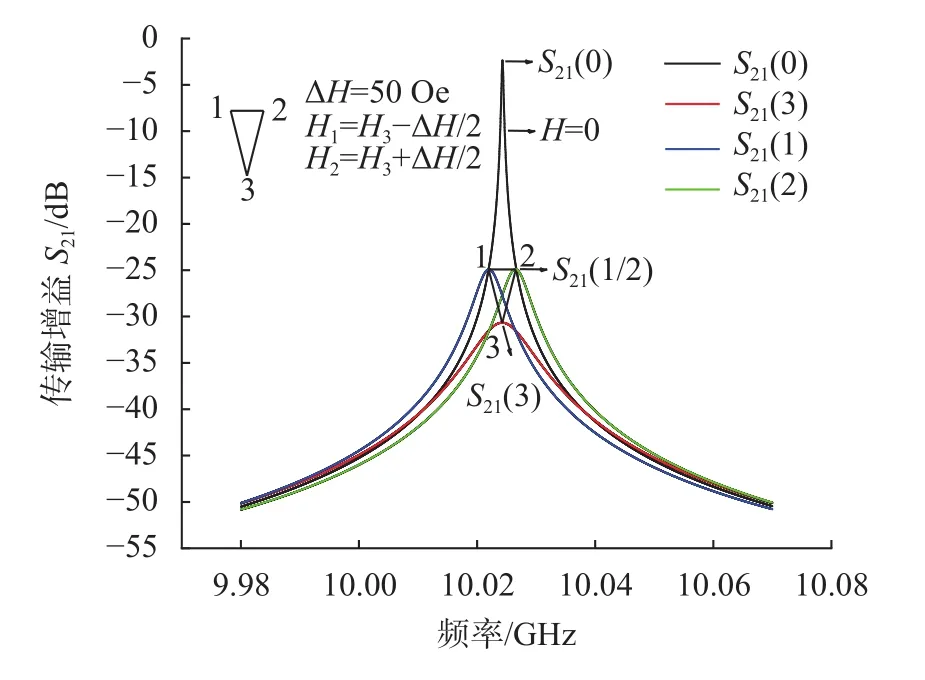
图3 共振线宽测试仿真示意图

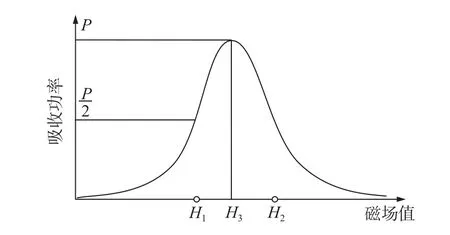
图4 样品吸收功率与偏置磁场值的关系

3）根据公式(3)[10]计算出S21(1/2)，然后找到使谐振曲线的峰值为S21(1/2)的偏置磁场值H1、H2。

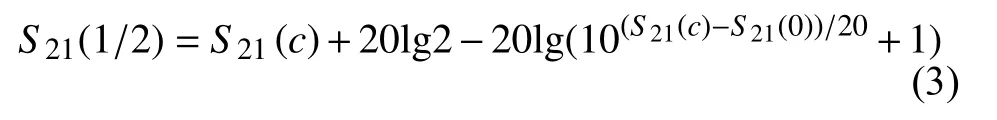
4）将H2-H1得到样品小球的铁磁共振线宽ΔH。

按照上述方法依次对直径0.4～1.7 mm（间隔0.1 mm）的样品进行测量，得到表1的测试结果（在测量中发现当小球直径达到1.8 mm时，谐振曲线发生塌陷，故没有测量结果）。

表1 各直径样品共振线宽测量结果

2.2 结果分析

由表1可知：随着样品直径增大，其铁磁共振线宽的测量结果大致呈递减趋势。将结果绘制成统计图，见图5，可以直观地观察这种趋势。

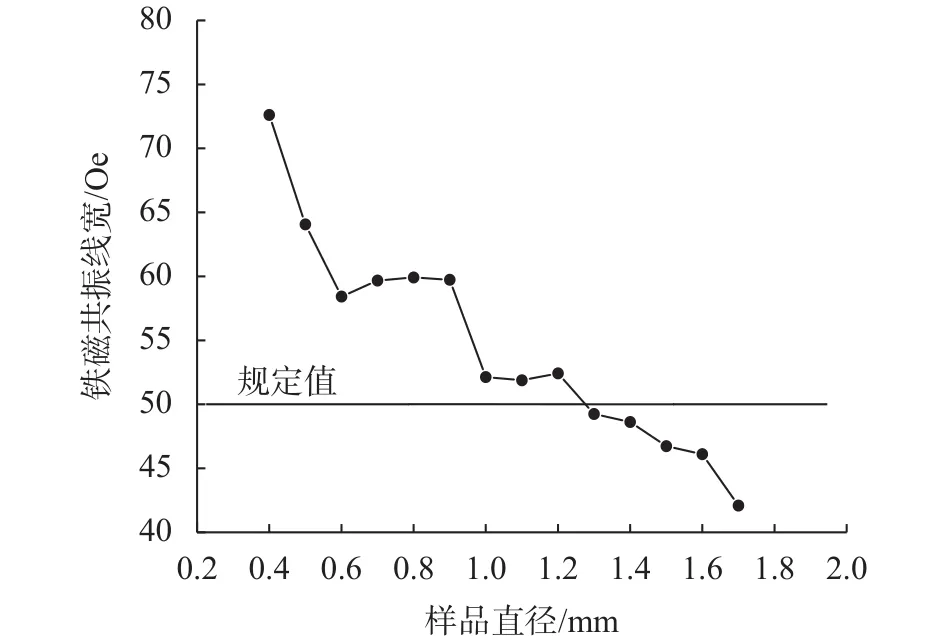
图5 不同直径样品共振线宽测量结果统计图

由图可知，在样品的共振线宽相同时，其尺寸大小对于测量结果有很大影响：随着样品直径增大，其铁磁共振线宽测量值逐渐减小，在不同的区间段内，变化的幅度大小不一。在样品直径介于1～1.4 mm时，获得的测量结果较好，测量误差稳定在5%以内，是样品直径选取的理想范围。

3 谐振曲线法

3.1 微扰理论尺度问题

根据谐振腔微扰法，样品的尺寸应该小于样品内的波长，样品内的波长[15]由以下公式得到：

式中：λ——波长；

v——微波在样品内传播的速度；

f——微波的频率（在文本中为10 GHz）。

由于样品体积很小，很难准确测得微波在样品内传播的速度，因此无法直接得到样品满足微扰理论的条件。

且在实际测量中，供应商还不具备制造所需样品的能力[16]，无法通过实际测试来探究样品尺寸满足微扰理论的尺度。

基于以上情况，本文提出了一种根据谐振曲线判断样品大小是否满足微扰理论的方法。通过电磁仿真软件，求解出样品达到铁磁共振状态时谐振腔的谐振曲线。研究发现，随着样品直径的增大，谐振曲线发生了坍塌，表明此时样品过大，不符合微扰理论。

3.2 测试过程及结果分析

在前文测量各直径样品的铁磁共振线宽时，记录下每个样品达到铁磁共振状态时谐振腔的谐振曲线进行观察比对，结果如图6所示。

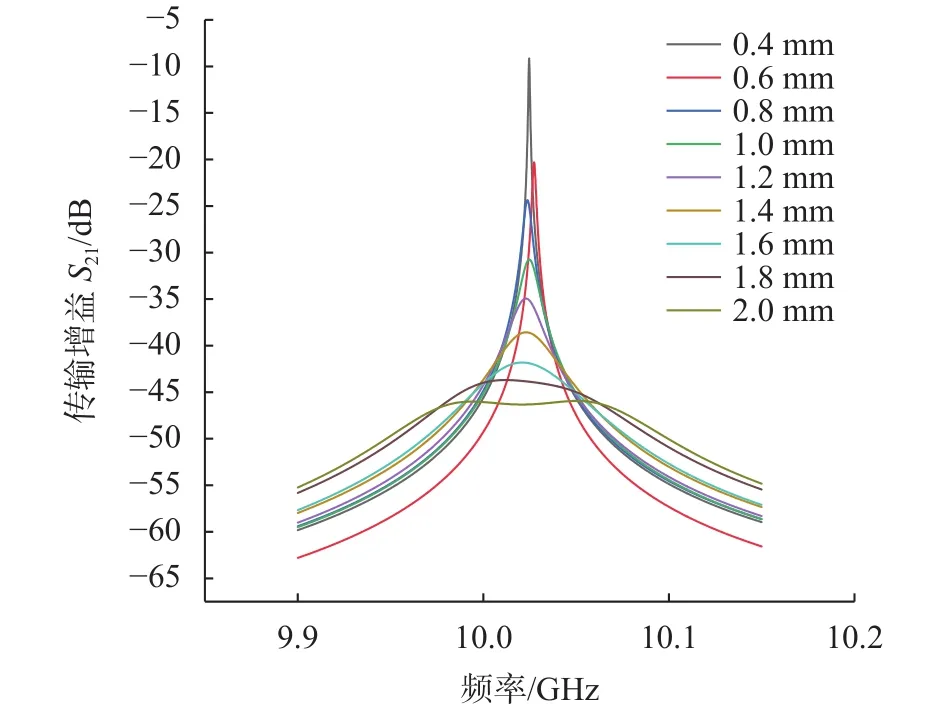
图6 各直径样品的谐振曲线

由测试结果可知：随着样品直径的增大，谐振曲线的峰值会减小并发生塌陷。在样品直径为1.8 mm时，谐振曲线已经发生塌陷，曲线峰值不再明显。当样品直径增大到2.0 mm时，谐振曲线呈现出了明显的塌陷，表明此时样品不再适用于微扰理论。在此基础上，对直径1.68 mm和1.78 mm之间的样品小球做了进一步测试。以求更准确地找出符合微扰理论的尺度，测试结果如图7所示。

图7 直径1.68～1.78 mm样品的谐振曲线

由图7可以看出在样品直径达到1.74 mm后，谐振曲线的波峰趋于平坦，峰值不再明显，呈现出将要塌陷的趋势。由此认为，此时样品已经不满足微扰理论，在本文的测试系统中，样品满足微扰理论的最大尺度为1.72 mm。

4 结束语

本文基于铁磁共振线宽对结构敏感的原理，研究了样品尺寸对铁磁共振线宽测量结果的影响。研究发现：在10 GHz下，铁磁共振线宽的测量结果会随样品直径的增大而减小，样品直径的理想选取范围为1～1.4 mm。需要提出的是，由于样品放入谐振腔会对腔内原有电磁场产生影响，所以实际测量中，为保证样品对腔内原有电磁场是足够小的微扰，并且参照国家标准中样品直径不大于1 mm的要求，样品直径可选取为1 mm。

本文针对满足微扰理论的尺度难以探究的问题，提出了一种通过谐振曲线来判断样品是否满足微扰理论的方法：随着样品直径增大，谐振曲线的峰值会逐渐减小，当谐振曲线的峰值不再明显、波峰平坦，则说明此时样品已不符合微扰理论。实验结果表明，通过该方法可以有效找出样品满足微扰理论的尺度。