角位置误差对回转误差测量的影响规律研究

张 志，夏仰球，米 良，周怡帆，谢罗峰，殷 鸣

(1. 中国工程物理研究院 机械制造工艺研究所，四川 绵阳 621900; 2. 四川大学机械工程学院，四川 成都 610065;3. 国家机床产品质量监督检验中心（四川），四川 成都 610200）)

0 引 言

由于空气静压支承的超精密主轴具有低摩擦、高精度的性能，被广泛应用于超精密机床和测量设备中。在超精密主轴的设计、制造、安装等过程中，由于各种不确定因素的存在，会导致超精密主轴本身产生运动误差，这些误差通常包括轴向误差、径向误差以及角度偏摆等[1-2]。有实验结果表明[3]：精密车削的圆度误差约有30%～70%是由于主轴轴线的径向回转误差引起的，且加工的精度越高，所占的比例越大。因此，进行超精密主轴的旋转轴线径向回转误差的精密测量十分必要。

径向回转误差测量主要有打表法、单点法、多点法等[4-5]。以上方法是使用位移传感器对安装在旋转轴线上的标准器进行测量的，在测量过程中会不可避免的引入标准器形状误差和标准器安装偏心误差，因此，对于超精密测量必须采用误差分离技术将旋转轴线径向回转误差分离出来[6-7]。目前常用的误差分离方法有反转法、多步法、多点法，这三种方法分离得到的径向回转误差都能达到纳米级别[8]。

从理论上讲，误差分离方法可以将标准器形状误差从旋转轴线径向回转误差中完全分离，但是在实际测量，尤其是超精密测量中，会存在许多因素导致测量的结果不精确，从而影响分离的径向回转误差。国内外学者对这些影响径向回转误差测量的因素进行了许多分析研究。Cappa等[9]对测量中的误差源进行了分析，指出标准器和传感器的位置误差、传感器的倾斜和未对准误差、标准器的偏心等都会对旋转轴线径向回转误差造成影响，并进行了定量地计算。崔海龙等[10]基于反转法研究了旋转轴线电机驱动、反转前后角度误差、工件偏心量、轴向运动误差对径向运动精度的影响。陈衡等[11]运用反转法对超精密主轴旋转轴线的回转误差进行了测量，对测量过程中导致测量不准的一些因素，如传感器测量球面靶标的非线性误差、电容传感器安装误差引起的测量误差以及环境因素的影响进行了研究，并提出了一个完整的回转误差不确定度评定过程。Marsh等[12]在比较3种误差分离方法的试验中指出，旋转轴线的转动不稳定会引起测量数据中角度和位移的不同步，但未就可能引起的测量误差展开分析研究。

在测量中由于编码器误差、安装误差、电机转矩波动以及环境扰动，传感器自身误差[13-14]等不确定因素，会造成旋转轴线转动速度波动而使转动角度实际值与理想值不一致，两者差值即为角位置误差。从以上相关研究可以看出，在众多的影响因素中角位置误差是影响旋转轴线回转误差测量不准的因素之一，但尚未发现有关角位置误差对径向回转误差测量影响规律的系统性研究。因此本文在前人研究的基础上，通过分析基于反转法的超精密径向回转误差测量原理，建立角位置误差对传感器位移测量影响的数学模型，基于模型仿真分析了角位置误差对位移测量误差和径向回转误差分离结果的影响，并进行了试验验证。

1 超精密径向回转误差测量原理分析

1.1 径向回转误差的误差分离技术

在进行旋转轴线径向回转误差测量时，实际的旋转轴线是不可见的，无法直接对其进行测量，因此通常需要用传感器对装在主轴的标准器(标准球、标准棒等)进行测量来间接测量旋转轴线的径向回转误差，然而标准器存在圆度误差和安装偏心误差，因此传感器测得数据中会不可避免的混入标准器的圆度误差和偏心误差[15]。对于纳米级的超精密径向回转误差测量，混入的圆度误差和偏心误差会对径向回转误差产生不可忽略的影响，必须用误差分离技术从传感器测量数据中分离并去除标准器的圆度误差和偏心误差，从而得到精确的回转误差，如图1所示。

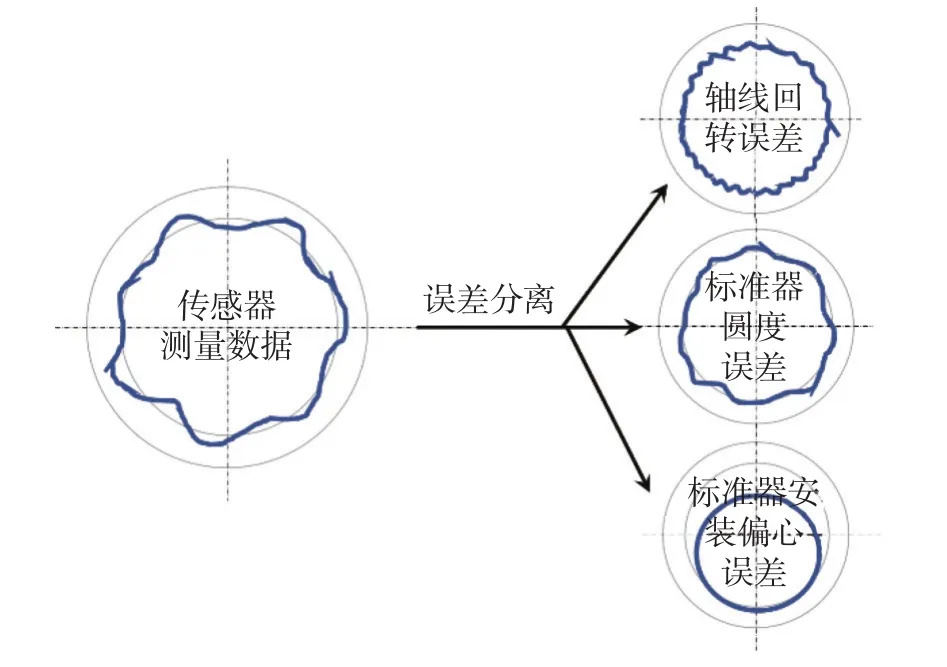
图1 误差分离示意图

1.2 反转法测量原理

反转法是诸多误差分离技术中的一种，其基本原理如图2所示。首先轴线旋转一圈，位移传感器获得不同角度 φ的位移数据T(φi)；接着将标准器(标准球或标准棒)和位移传感器相对于旋转轴线同步旋转180°，轴线再旋转一圈，获得T′(φi)。其中T(φi)，T′(φi)均包含有标准器的圆度形状误差信号和旋转轴线的径向回转误差信号，并有如下关系：

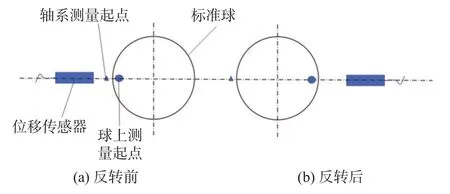
图2 反转法原理图

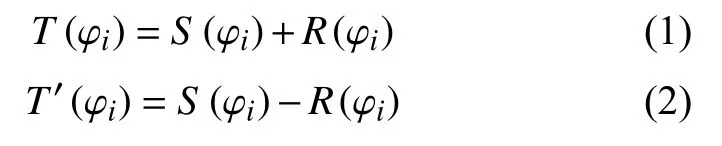
式中：S(φi)——标准器的圆度误差信号；

R(φi)——旋转轴线径向回转误差信号。

由式(1)和式(2)，容易得到标准器圆度误差R(φi)和主轴径向回转误差S(φi)：

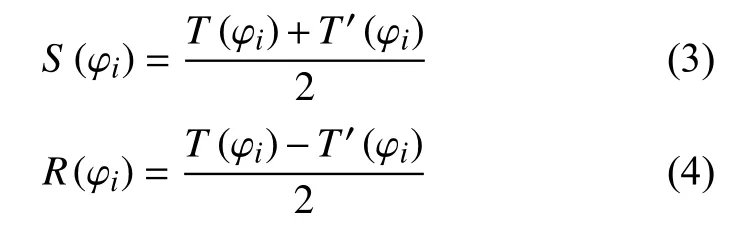
在理论上，用反转法可以将传感器测量数据中的径向回转误差和标准器圆度误差完全分离。但是从式(3)和式(4)可以看出，角度参量直接作用于R(φi)和S(φi)，即使分离后角位置误差也将是影响传感器测量数据准确性的因素之一。在实际测量中，由于传感器安装误差、标准器偏心量、反转角度误差、环境波动等原因，传感器测量数据会存在误差，进而导致分离得到的径向回转误差和圆度误差与理想值存在偏差，已有相关文献对此开展研究[10,12]，本文不再赘述。下面将重点针对角位置误差对传感器测量误差及最终导致的回转误差测量误差产生的影响展开分析。

2 角位置误差影响的数学建模

在进行径向回转误差测量时，通常需要用位移传感器获得位移数据，然后通过后期的数据处理，分离误差得到径向回转误差。角位置误差的存在会影响位移传感器获得的位移数据的准确性，因此首先需要分析角位置误差对传感器测量位移的影响。

在用标准球测量径向回转误差时，标准球的理想位置应与旋转轴线同心。但由于安装误差、制造误差等因素，会不可避免地引入偏心而使标准球不在理想位置。设点O为旋转轴线回转中心，标准球半径为R，由于存在标准球安装偏心e，所以设标准球的球心为O′，如图3所示。

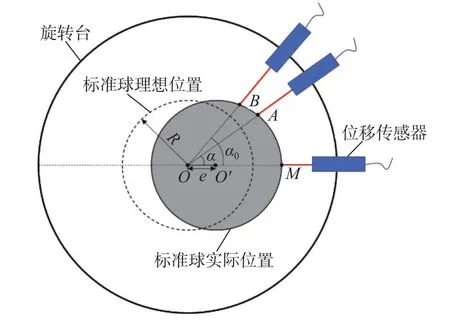
图3 存在偏心误差时的标准球位置

实际测量中，标准球绕旋转轴线回转中心转动，而传感器相对旋转轴线回转中心不动。假设起始位置为位移传感器轴线与标准球球心偏心矢量同轴的位置，不考虑位移传感器倾斜误差。当旋转轴线转动角度 α时，位移传感器测量点从初始位置M变为A。但是由于标准球安装偏心的存在，当出现角位置误差 θ时，旋转轴线实际转动角度为 α0，位移传感器的实际测量点为B，如图4所示。显然位移传感器在A、B两点测得的位移值存在误差。因此，当在测量过程中出现角位置误差时，会导致测量点发生变化；由于标准球安装偏心误差的存在，传感器在A、B两个测量点测得的位移值并不一致，LOA与LOB的差值即为角位置误差引起的位移测量误差。

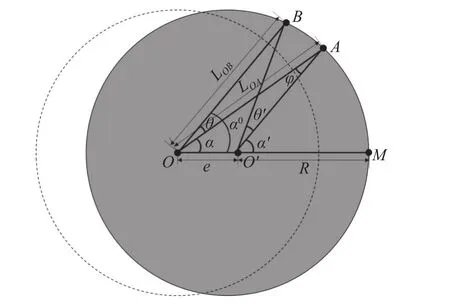
图4 角位置误差引起的位移测量误差

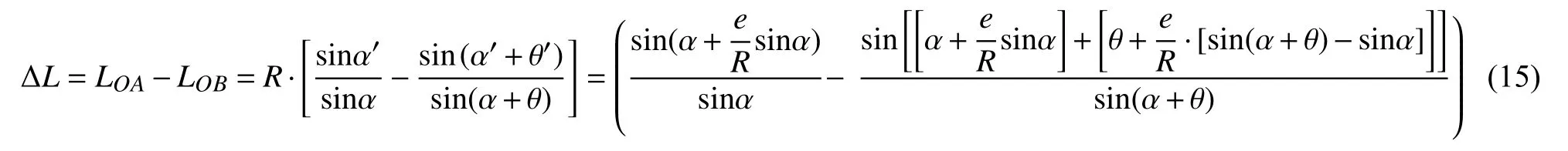
3 角位置误差影响规律分析

3.1 角位置误差对位移测量值的影响

从第2节的分析中可以知道，在使用标准球进行回转误差测量时，标准球会不可避免地产生安装偏心误差。由式(15)可知，由于标准球安装偏心e的存在，当标准球半径为R时 ，角位置误差 θ会引起传感器位移测量误差 ΔL。为分析角位置误差 θ对传感器位移测量值的影响，取标准球安装偏心e为1 μm、标准球半径为 0.5 in（1 in=0.0254 m），仿真计算角位置误差值从0.01°到0.10°时的位移测量误差的绝对值，结果如图5所示。

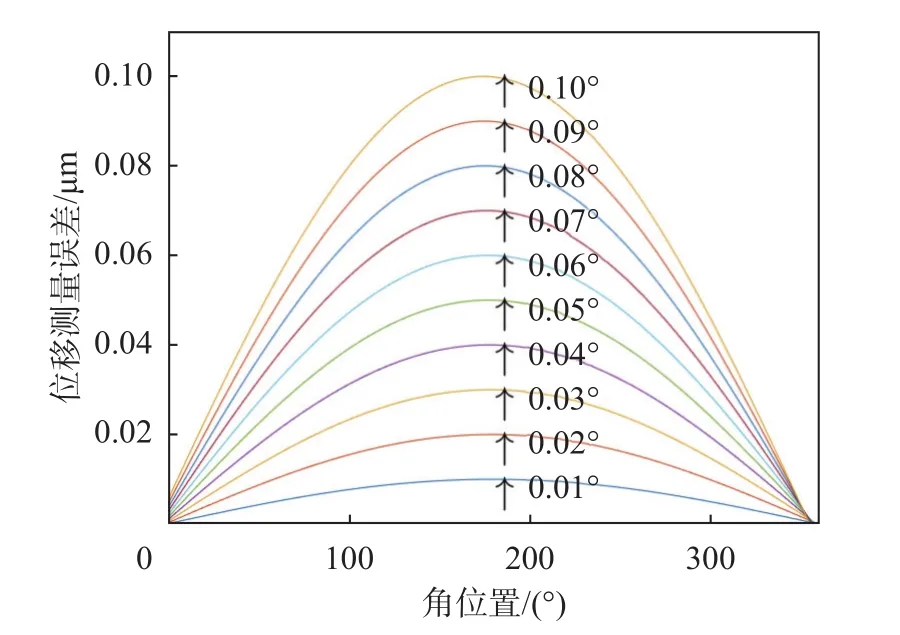
图5 角位置误差产生的位移测量误差

从图中可以看出：

1）在同一角位置处，角位置误差越大，产生的位移测量误差越大。如在180°时，0.01°的角位置误差带来的位移测量误差在0.01 μm左右，而0.02°的角位置误差带来的位移测量误差在0.02 μm左右。

2）角位置误差带来的位移测量误差存在最大值和最小值。最小值出现在位移传感器与标准球安装偏心方向一致时，最大值则出现在相反位置。如仿真中取图3中位移传感器与标准球安装偏心方向一致时的M点为0°位置，因而位移测量误差最小值在0°位置，最大值在180°位置。

3.2 角位置误差对径向回转误差分离结果的影响

角位置误差对传感器位移测量值产生影响，进而会对误差分离后的径向回转误差和标准球圆度误差产生影响。为了仿真分析角位置误差对径向回转误差分离结果的影响，第一步，产生一组理想传感器数据，使误差分离得到的径向回转误差和圆度误差均为0；第二步，将仿真得到的0.01°～0.1°的角位置误差产生的位移测量误差分别加到理想传感器数据中，再进行误差分离。将前后两步得到的误差分离结果相减，得到径向回转误差和圆度误差的差值如表1所示。

表1 角位置误差引起的径向回转误差和圆度误差的差值仿真值

从仿真的结果可以看出，分离出的标准球圆度误差及径向回转误差的差值将随着角位置误差单调递增，且对圆度误差的影响更为显著。角位置误差对径向回转误差分离结果的影响如图6所示。

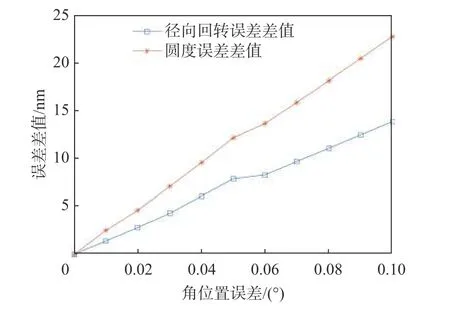
图6 径向回转误差和圆度误差的差值图

4 测试试验

4.1 搭建测量系统

搭建的径向回转误差测量系统如图7所示。测试系统主要由超精密转台、标准球、位移传感器、多尺分度台、数据采集系统（图中未显示出）等组成。超精密转台的标称回转误差为50 nm，转台内部嵌有双编码器，可以获得0.000 9″的角度分辨率，标准球标称圆度误差为50 nm，传感器采用电容式非接触位移传感器（Lion CPL350-C5S），传感器量程50 μm，线性度0.5%，分辨率0.7 nm。

图7 测量系统

4.2 测量试验

4.2.1 径向回转误差测量

利用搭建好的测量系统进行转台径向回转误差测量实验，然后采用反转法进行误差分离。测量前，通过自准直仪和多面棱体将转台的角度误差校准并补偿至0.002°以下，最大限度降低角度误差对回转误差的测试影响，然后调整标准球的偏心误差在1 μm左右，利用位移传感器从0°开始采集位移数据，采集频率为80 Hz，每圈采集点数为960。

为消除随机误差的影响，这里各选取了反转前、后测量数据中的20圈数据，对每个采集点的测量位移取平均值进行数据处理和误差分离，误差分离后得到径向回转误差和标准球圆度误差如图8所示，径向回转误差为49.6 nm，圆度误差为48.1 nm。标准球的标称圆度误差为50 nm，误差分离获得的标准球圆度误差值与标准球的标称值基本吻合。

图8 误差分离后得到径向回转误差和标准球圆度误差

4.2.2 引入角位置误差的径向回转误差测量

在实际测量中，角位置误差是变化的，每个测量点产生的角位置误差是不同的。在试验中，转台不做任何角度补偿的情况下，测量点的角位置误差大小在±0.05°内变化。 图9是引入角位置误差为0.05°时的误差分离结果，径向回转误差为62.6 nm，圆度误差为61.9 nm。与未引入角位置误差时的试验结果相比，径向回转误差增加了26.2%，圆度误差增加了28.7%，说明0.05°的角位置误差已经对回转误差分离结果产生了极大的影响。

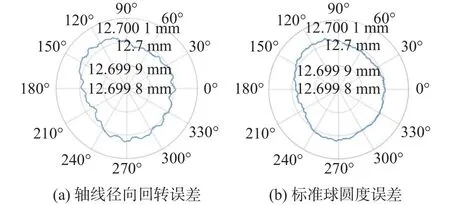
图9 角位置误差为0.05°时的误差分离结果

为获取角位置误差对径向回转误差测量结果的影响规律，在试验中引入0.01°～0.1°的角位置误差，试验方法如下：测量前调整标准球的偏心误差在1 μm左右，用位移传感器采集每个测量点加上0.01°到0.1°角位置误差后的位移值，同4.2.1一样每圈采集点数为960，并选取反转前、后测量数据中的20圈数据进行误差分离，误差分离结果如表2所示。将引入角位置误差后的径向误差分离结果和未引入角位置误差的径向误差分离结果作比较，得到径向回转误差和圆度误差的差值如表3所示。

表2 引入角位置误差后的误差分离结果

表3 试验中角位置误差引起的径向回转误差和圆度误差的差值

仿真结果与试验结果对比如图10所示，仿真结果与试验结果均显示出：标准球圆度误差及径向回转误差的差值将随着角位置误差的增大而增大，且对标准球圆度误差的影响较为显著。试验得到的差值比仿真值得到的差值大是由于试验中还存在其他的影响因素使测量的位移值不准确，如传感器的倾斜和未对准误差、轴向运动误差等。

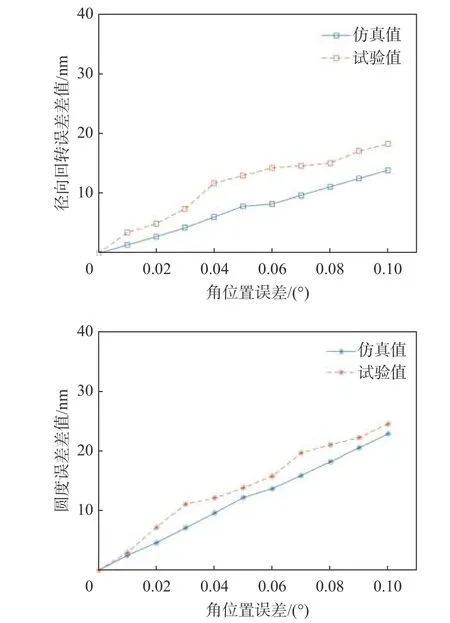
图10 仿真结果与试验结果对比图

5 结束语

在超精密主轴回转误差测量中，角位置误差会引起位移传感器产生测量误差，进而对径向回转误差分离结果产生影响。建立了角位置误差对传感器位移测量影响的数学模型，从数学模型中可知，标准球安装偏心、角位置误差会对传感器位移测量值产生影响，进而会影响旋转轴线回转误差分离结果的准确性。采用反转法进行回转误差分离，在进行了角位置误差对旋转轴线回转误差分离结果影响的仿真和试验后，仿真结果与试验结果均显示出：标准球圆度误差及径向回转误差的差值将随着角位置误差的增大而增大，且对标准球圆度误差的影响较为显著。