提高供热机组的调峰灵活性研究

郭良丹，谭 锐，林宝森，殷 戈，伍仁杰，蒋国安，柯展煌，严晓生

(1. 国能南京电力试验研究有限公司，江苏 南京 210046; 2. 国能（泉州）热电有限公司，福建 泉州 362804）)

0 引 言

面对化石能源日渐枯竭的能源问题，人们关注的焦点从传统能源发电转移到了太阳能、潮汐能等新能源发电上，新能源发电产业也因而得到了快速发展[1-2]。在新能源发电大规模并网背景下，本身调峰能力受限的供热机组不能同时满足电、热负荷需求，这给电网调度带来了极大的负担[3-6]。国家能源局发布通知要求加强对供热机组调峰性能监管，鼓励供热机组通过增加储热装置提高负荷调节能力，协调电力调度机构和热力调度机构优化热电运行方式[7]。

面对供热机组灵活性改造的热潮，张倩男[8]利用Gambit软件对热水蓄热罐进行几何建模，数值模拟了热水蓄热罐在蓄放热过程中斜温层的变化规律；杨利[9]采用Ebsilon软件搭建热电联产机组运行优化分析模型，对某电厂亚临界2×330 MW热电联产机组配置储热罐后运行方式及优化效果进行分析计算；王惠杰等[10]基于Aspen plus软件搭建了供热机组配置储热装置的仿真模型，并研究供热机组配置储热装置后的调峰范围；Dai等[11]以蒸汽的三级传热模型和基于夹带耗散的热阻理论为基础，给出了一个考虑常规火电机组、VRESs和带相变TES装置的热电联产机组的综合电力热力调度模型，并提出了求解该非线性规划问题的迭代方法。Hu等[12]为提高热电联产系统的可调性，在热电联产系统中安装相变储热装置，提出用热阻网络分析集成系统，用线性规划方法优化集成系统的运行方式，为供热系统的优化设计提供指导储存设施。

本文提出在热网侧增设热水储热罐的方法以提高供热机组的调峰灵活性，并基于某地区的热负荷、电负荷变化情况提出了两种储热模式、计算了两种储热模式下储热罐的储热容量。此外为确定最佳调峰调度方案，分析了两种储热模式在调峰范围、放热速度和热经济性3个方面的差异。由于此深度调峰方法的影响因素复杂多变，目前并没有具体的应用方案，因此本研究内容在实际应用中具有重要的参考意义。

1 储热罐参与供热机组调峰原理

热网侧在不增设储热罐的情况下，供热抽汽总焓降与热负荷保持动态平衡，供热抽汽传热给热网循环水，该过程的能量守恒方程如下：

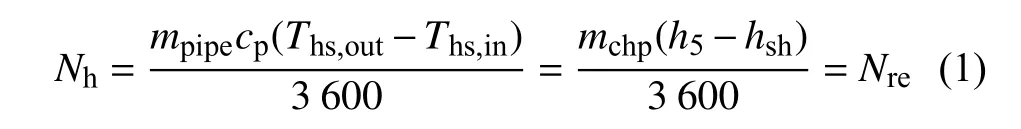
式中：mpipe，mchp——供热循环水流量和供热抽汽量，t/h；

cp——定压比热容，kJ/(kg·℃)；

Ths,out和Ths,in——热网供回水温度，℃；

h5，hsh——供热抽汽焓值，疏水焓值，kJ/kg；

Nh，Nre——热网负荷和机组供热负荷，MW。

供热机组的最大供热抽汽量即供热能力是随着电负荷变化的，也这正是这种制约关系导致机组不能同时满足一直变化的电、热负荷需求。而增设储热罐可改善这种情况，当机组的供热能力可满足热负荷且有富余时，按机组最大供热抽汽量抽汽，抽出来的热蒸汽一部分用来供热，另一部分用来储热；当机组供热能力不能满足热负荷时，储热罐则放热来弥补机组供热不足[13-14]。其中储热罐最小容量mtes可由公式(2)计算出：

以24 h为周期，若储热罐储热量大于夜间采暖所需且放热速度足够快，机组可以在夜间停止供热，供热完全由储热罐承担，这时机组可同纯凝机组一样灵活调峰；若储热罐储热量小于夜间采暖所需，机组可在夜间减少供热抽汽，与储热罐共同供热，此时储热罐用来补充机组因调峰导致的供热不足。

2 供热机组耦合储热罐模型

该供热系统分为供热机组、换热站、储热罐三个部分，其中热水储热罐是与热网循环水联通的。机组供热抽汽mstm,hs经过热网换热器将热网循环水从Ths,in加热到Ths,out，当机组的供热能力大于热网负荷时，Ths,out会过高超出热网的采暖需求，将该温度过高的热网水分成两部分：一部分与储热罐释放的冷水混合供热，另一部分存储在储热罐中；当机组的供热能力小于热网负荷时，供热抽汽量不足以满足热负荷需求时，将热网回水分成两部分：一部分进入热网加热器加热，而后与储热罐释放的热水混合供热，另一部分存储在储热罐中。

为分析供热机组耦合储热罐后的调峰能力变化、储热罐的响应情况及等效煤耗率的变化情况，使用EBSILON软件搭建了供热机组耦合热水储热罐的仿真模型，如图1所示，并添加了time series序列，以便于分析储热罐的放热特性。

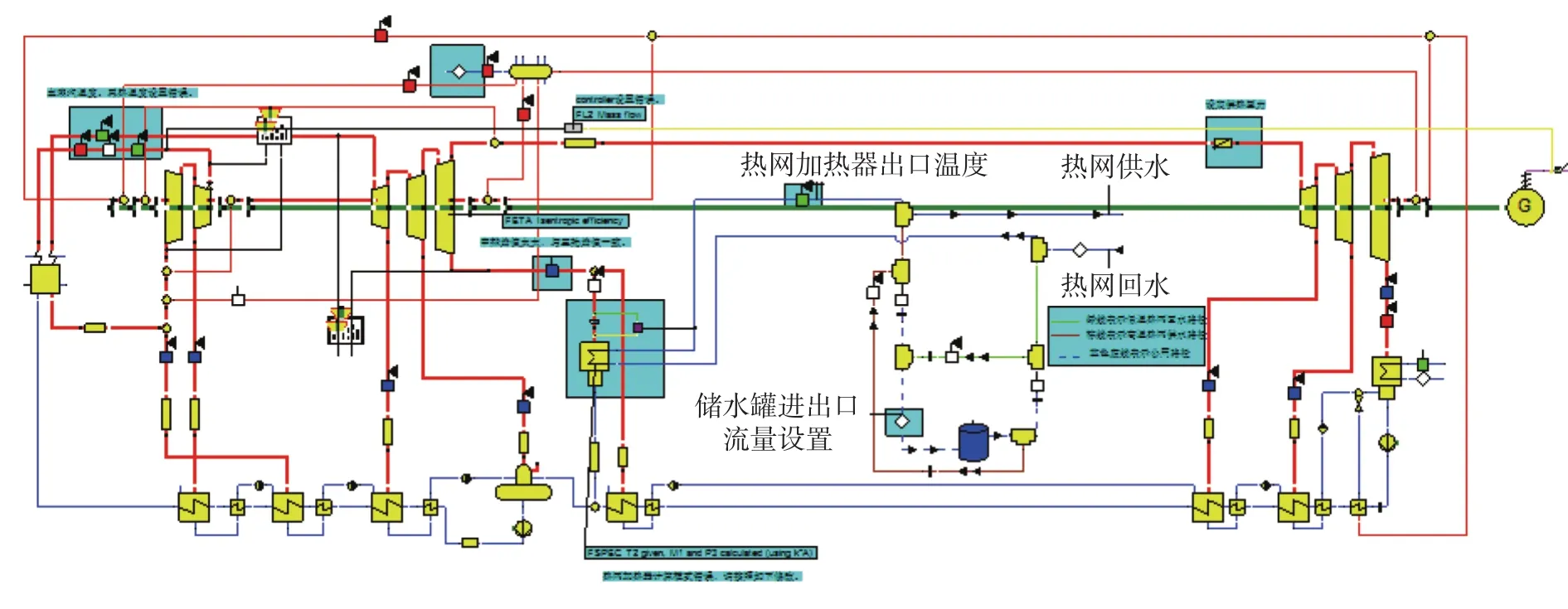
图1 供热机组耦合储热罐的EBSILON模型

3 利用储热优化电热调度

3.1 日运行电热调度分析

某地区采暖期某一天的热负荷需求变化情况见表1，电负荷需求变化情况如图2所示。

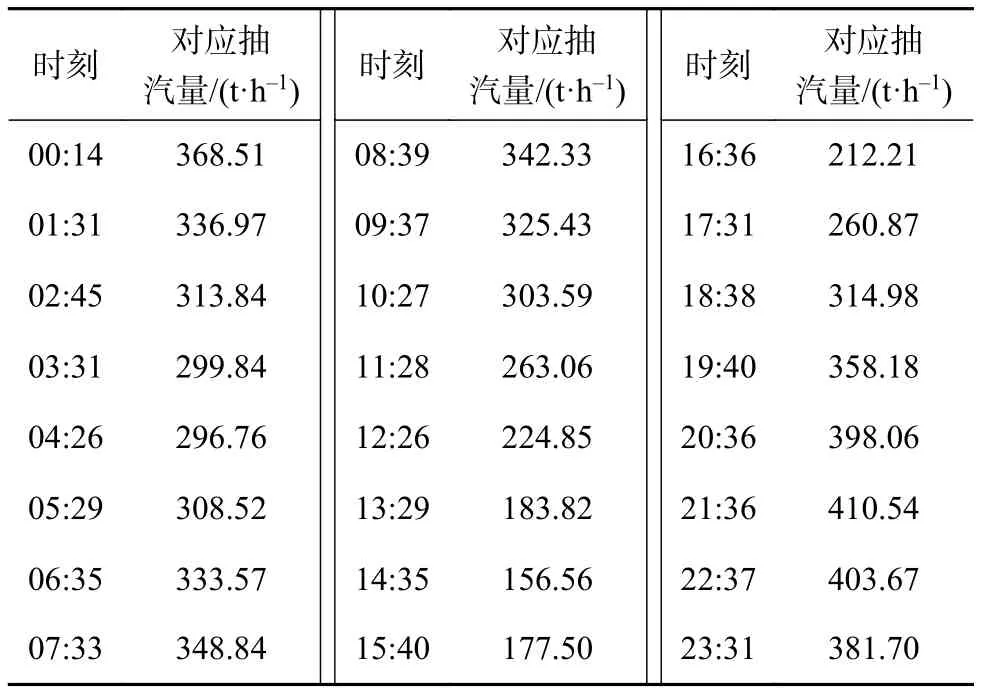
表1 热负荷折算的供热抽汽量

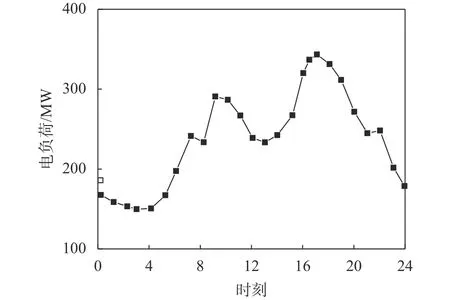
图2 某地区某一天的电负荷变化图

现已知一天中各时刻所需的电量和供热抽汽量，供热机组的调峰能力却不能一直满足需求。本文通过储热解决该问题，需先确定具体哪些时刻电网负荷超出了供热机组的调峰能力。

首先通过EBSILON软件搭建的供热机组仿真模型，计算出机组的安全运行区域，即图3点ABCDE围成的区域。

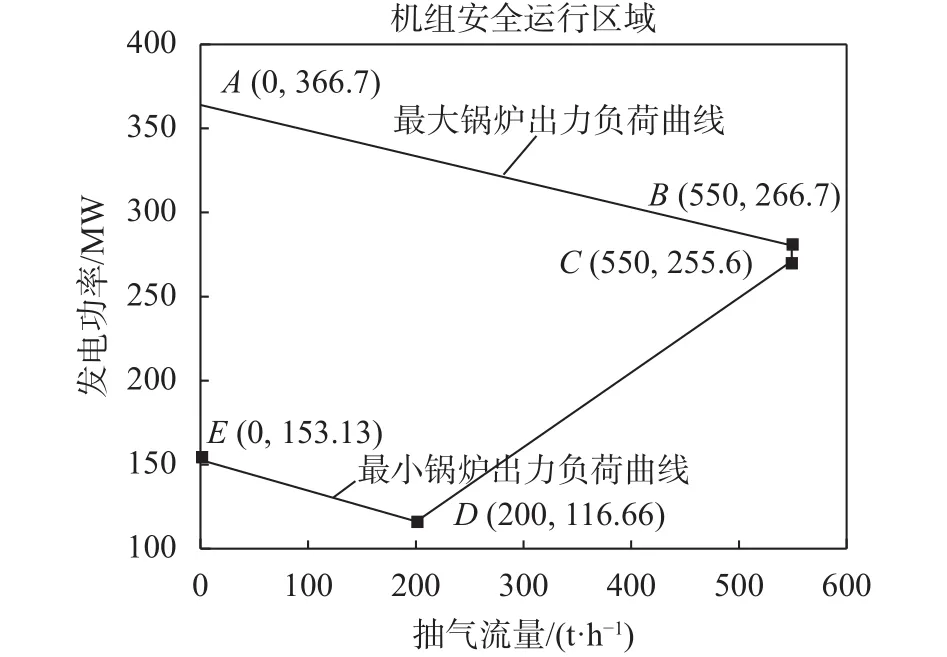
图3 某供热机组安全运行区域

具体地讲，首先确定最大锅炉出力负荷线AB，该线代表的各工况主蒸汽流量均为1180.007 t/h，其中A点为最大发电负荷工况（0，366.7 MW），B点为额定供热负荷工况（550 t/h，266.7 MW）。其次确定额定供热工况下的最小发电负荷，经过迭代计算可以得到额定供热工况下的最小发电负荷工况C点(550 t/h，255.6 MW）。接下来确定最小锅炉出力负荷曲线ED，其中E点是机组稳态运行最小凝气工况点（0 t/h，153.13 MW），点D是锅炉稳定在最小出力情况下的最大供热抽汽工况，为（200 t/h，116.66 MW），此时不能再增加供热抽汽流量，这是因为要保障低压缸最小进汽流量。

机组的安全运行区域确定后可以得到机组各供热工况下的调峰范围，如图4所示。

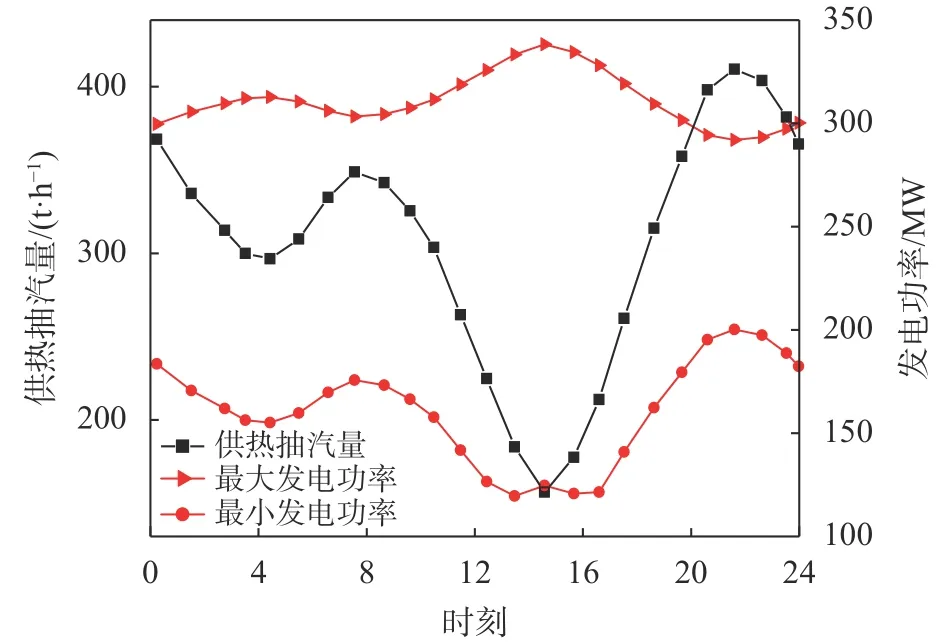
图4 “以热定电”模式下供热机组调峰范围

由图4可以看出，当供热抽汽流量减小时，机组最大发电功率增大，最小发电功率减小，即调峰范围增大，反之当供热抽汽流量增大时，调峰范围减小。但14:00左右最小发电功率有微小上升，这是因为限制机组最小发电功率的因素发生改变，从低压缸最小进汽流量限制转为最小主蒸汽流量限制。

为确定具体哪些时段内供热机组无法完成电网调峰，将同一时间电网负荷变化曲线和供热机组调峰范围曲线在同一图中绘出，见图5。

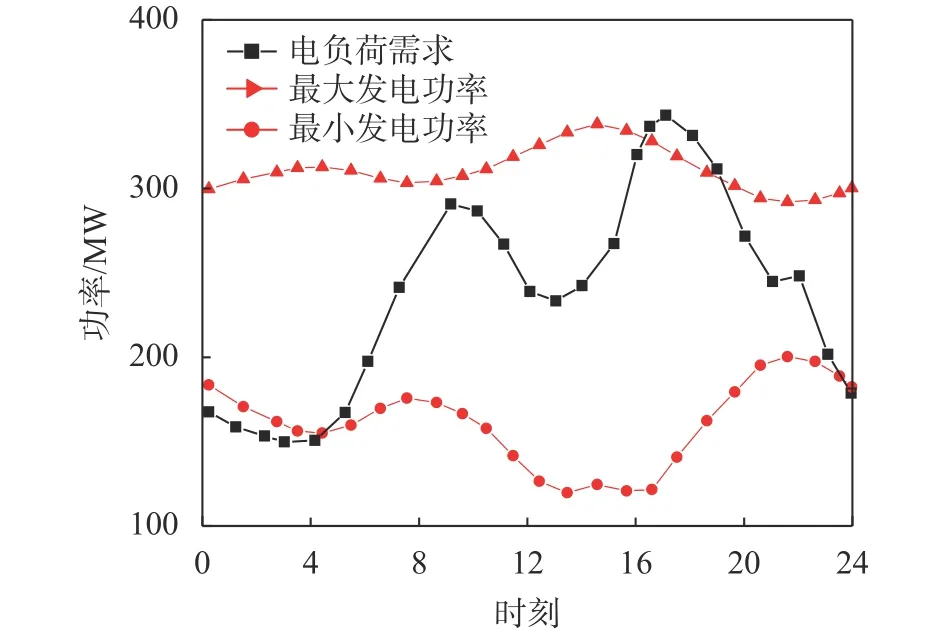
图5 电负荷与调峰范围曲线

由图5可以看出，电网负荷曲线不是一直介于代表调峰范围的两条红线之间，23:30至4:30时段供热机组最小发电功率大于电网负荷，在16:30至19:30时段供热机组最大发电功率小于电网负荷，无法满足电用户需求。这两时段的情况均是由机组供热调峰范围变小导致的。若这两时段内机组减少抽汽供热或者不抽汽供热，用储热罐替代机组供热，机组便可满足电网调峰要求。

3.2 储热调节方案

机组的安全运行区域确定后还可求出各工况下的调峰抽汽余量。计算公式如下所示：

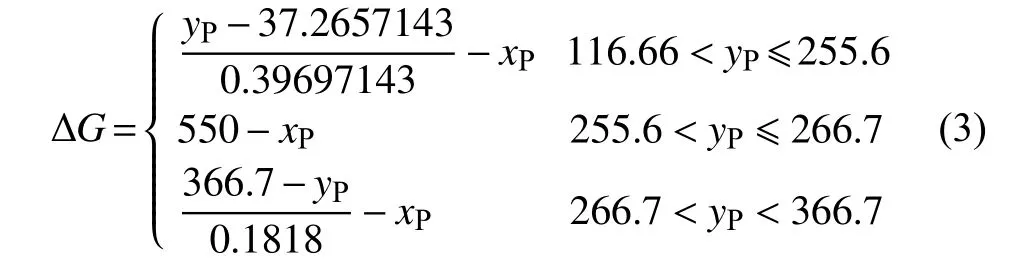
若ΔG＞0，说明此时机组在满足热用户、电网需求的情况下还可以抽出更多的蒸汽用来储热，若ΔG＜0或ΔG=0，说明此时机组已经达到了调节上限，无法抽出多余的蒸汽用来储热。另外使用式(3)对时间积分还可得到总抽汽余量。而总抽汽余量是否足够填补上述两个时段机组为满足电网调峰减少的供热蒸汽量，关系到使用储热罐调峰的可行性。

现将各时刻的供热抽汽量和最大供热抽汽量在同一图中绘出，见图6。红色曲线低于黑色曲线时，意味着机组此时的供热抽汽量已经达到了该发电负荷下的最大供热抽汽量，若再强行增大供热抽汽，低压缸进汽流量将小于临界值，影响机组安全运行。

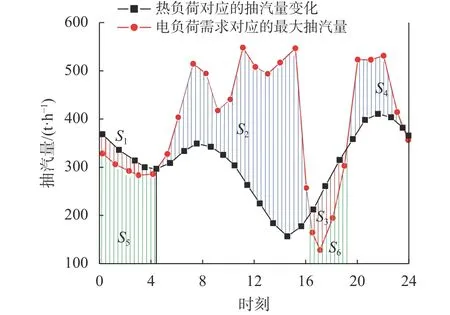
图6 供热抽汽量和最大供热抽汽量变化

在机组可以同时满足电网调峰和供热的时段内，机组还能抽出比采暖需求更多的高温蒸汽，抽汽余量总量Q1在图6中表示为蓝色阴影区域面积，求解公式如下：

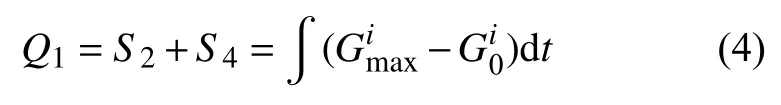
通过积分公式求解出图6中蓝色阴影区域面积Q1≈2 600 t。机组不能满足电网调峰的两个时段，可使用储热罐移峰填谷来满足电网调峰。其中储热罐有两种调节模式可采用，一种是储热罐提供部分供热负荷模式，即在满足电网调峰的条件下，储热罐放热填补机组为满足电网调峰减少的供热。在这种模式下，需要求出该时段内出各发电负荷下的最大供热抽汽量，再用各时刻所需的采暖抽汽量减去最大供热抽汽量，得到各时刻采暖所缺的抽汽量，将其对时间积分，便可得到该模式下储热罐的最小容量Q2；另一种是储热罐提供全部供热负荷模式，即该时段内机组直接中断供热，供热完全由储热罐承担。在这种模式下，将各时刻采暖所需的供热抽汽量对时间求积分，可得到供热机组中断供应情况下储热罐的最小容量Q3。计算公式如下：

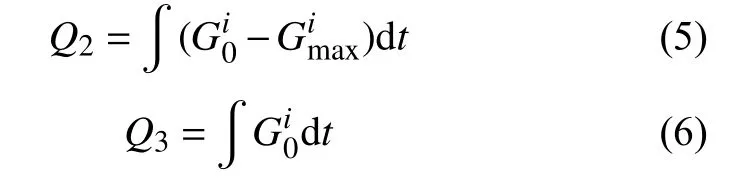
式中：G0—各时刻采暖所需的供热抽汽量；

Gmax—各时刻发电负荷下的最大供热抽汽量。

通过积分可以求出图中各阴影区域面积：Q2=S1+S3=401.51 t，Q3=S1+S3+S5+S6= 2 352.45 t。Q1大于Q2和Q3，这说明总抽汽余量足够补充为电网调峰减少的供热，且两种储热调节模式均可行。

4 储热调节方案对比分析

从总抽汽余量上看两种储热调节模式都能满足电网和热网的需求，但具体采用哪种模式还需对调峰范围、供热响应和热经济性进行对比。

4.1 调峰区间对比

根据两种储热调节模式的设计思路求出各时刻的抽汽流量并作图7，其中4:30到16:00时段机组供热抽汽较多，超出采暖所需，超出部分储存在储热罐中。在储热罐提供部分供热负荷模式中不需要这么多的热量，到9:30时储热罐已储有500 t，大于Q1足以供热，可停止储热过程。现已知两种模式下机组各时刻的供热抽汽流量，将相关数据代入机组仿真模型中，可计算出供热机组对应的调峰范围，并将其与电网负荷比较作图8。

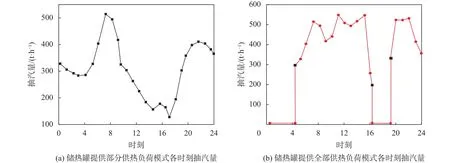
图7 两种储热调节模式中抽汽量变化

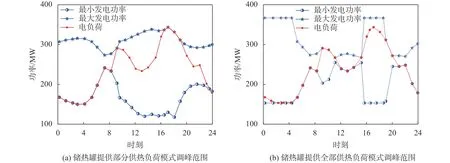
图8 两种储热调节模式中调峰能力变化

通过图7(a)、(b)可以发现两种储热调节模式的供热抽汽量瞬时值是不同的，储热罐提供部分供热负荷模式中抽汽量变化曲线比较平滑，07:17时抽汽量瞬时值达到最大514.3 t/h，17:07时抽汽量瞬时值达到最小128 t/h。储热罐提供全部供热负荷模式中抽汽量变化曲线出现两次突变，第一次突变在04:18时抽汽量瞬时值从0 t/h跳跃到327.5 t/h，第二次突变是在16:36时抽汽量瞬时值降低到0 t/h，并在0抽汽状态持续了3 h。另外图7(a)、(b)图中两曲线与x轴围成的面积基本相同，说明供热抽汽总量相等，与采用哪种模式无关。根据图8(a)、(b)可知，两种储热调节模式下红线始终位于两条蓝线之间，这说明使用储热罐供热后机组各时刻的调峰范围均可满足电网调峰。

4.2 储热罐放热速度对比

依照两种储热调节模式中的设计参数，在EBSILON耦合储热罐模型上增加时间序列，模拟储热罐放热过程，并将储热罐各时刻的平均放热速度变化情况列在表2中。由于机组联合储热罐供热属于水侧联动，因此传热过程很快，热负荷变化时响应也很快，不影响热用户感受。MJ/s

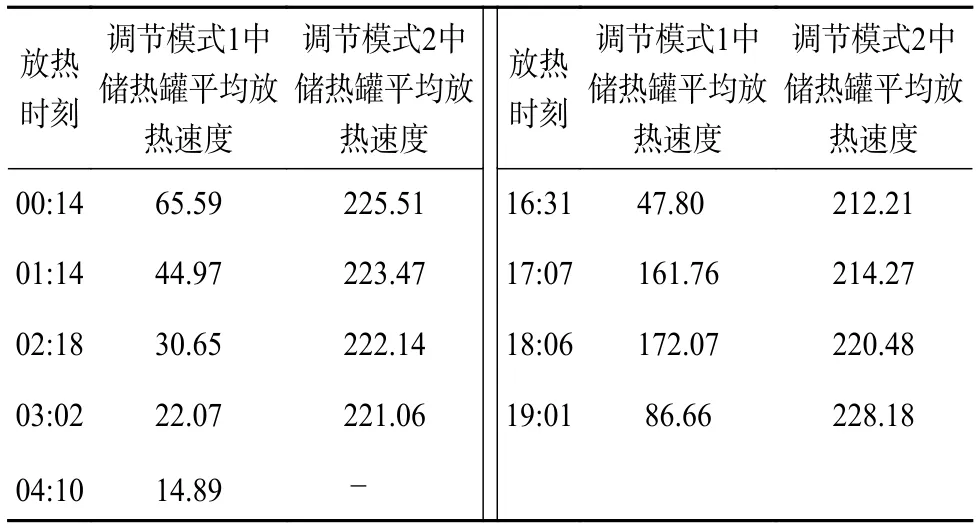
表2 储热罐在各时刻的平均放热速度

由表2可以看出，储热罐提供部分供热负荷模式中储热罐的放热速度小于储热罐提供全部供热负荷模式，这是因为储热罐提供全部供热负荷模式是直接由储热罐热水和热网回水直接混合换热，换热温差大，而储热罐提供部分供热负荷模式则是储热罐热水与与热网加热器加热后的热网回水混合换热，换热温差小。但储热罐提供全部供热负荷模式对储热罐参数要求更高。

4.3 等效煤耗对比

等价煤耗法是将供热获得的效益折合成发电后，与实际发电量相加，便得到机组等价发电量，从而算出机组的等价煤耗率。该方法既能算出等价煤耗率，又可体现出供热机组的热分摊比[15]。等价发电量计算公式如下：

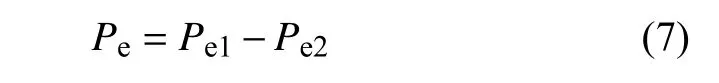
式中：Pe1——供热机组实际发电量，kW；

Pe2——供热机组供热量效益转化的发电量，kW。

其中，Qr为供热机组供热量，GJ/h；sr为单位热量的热价，元/GJ；sw为单位电价，元/GJ；Dr为机组供热抽汽流量，t/h；ir为机组供热抽汽焓，kJ/kg；ih为机组供热抽汽经换热后的焓值，kJ/kg。机组煤耗可由下式算出：

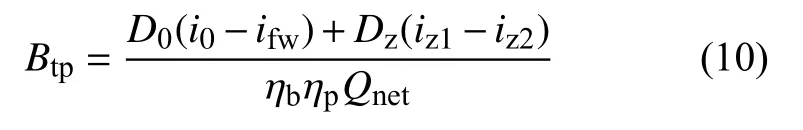
其中，ηb和ηp为锅炉和管道效率；Qnet为标准煤热值，kJ/kg；Btp为供热机组煤耗量，t/h；D0和Dz为主蒸汽和再热蒸汽流量，t/h；i0和ifw是主蒸汽焓和给水焓，kJ/kg；iz1和iz2为热、冷段再热蒸汽焓，kJ/kg。等价煤耗率为：

通过EBSILON机组耦合储热罐仿真模型模拟两种储热调节模式，可以得到计算等效煤耗所需参数，进而可计算出煤耗率随供热抽汽量的变化情况，如图9所示。

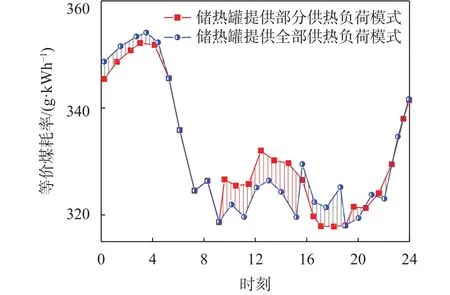
图9 等价煤耗率变化

对比图9中两种模式下的等价煤耗率变化曲线，前9个小时红线在蓝线下方，储热罐提供部分供热负荷模式下等价煤耗率更低，热经济性更好，09:00到15:42时段蓝线在红线下方，储热罐提供全部供热负荷模式下等价煤耗率更低，热经济性更好，15:42时之后红线基本位于蓝线下方。尽管如此却不能从总时长上判定采用哪种模式，而是将两条曲线对横坐标时间积分再比较大小来确定采用方案。即：

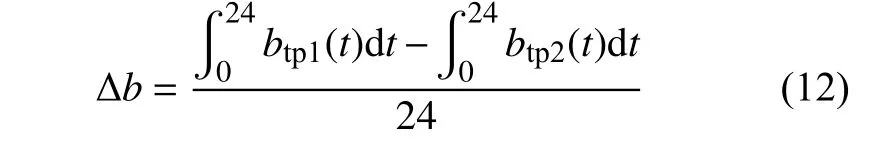
其中btp1(t)，btp2(t)分别为储热罐提供部分供热负荷模式，储热罐提供全部供热负荷模式中t时的等价煤耗率。

若Δb＞0，说明储热罐提供部分供热负荷模式下煤耗量更多，采用储热罐提供全部供热负荷模式更经济；若Δb＜0，说明储热罐提供全部供热负荷模式下煤耗量更多，采用储热罐提供部分供热负荷模式更经济。经积分求解储热罐提供部分供热负荷模式平均等价煤耗为370.42 g/kWh，储热罐提供全部供热负荷模式平均等价煤耗为357.17 g/kWh，Δb=13.25＞0，说明储热罐提供全部供热负荷模式更经济。

5 结束语

1) 两种模式下的供热抽汽量瞬时值是不同的，储热罐提供部分供热负荷模式中供热抽汽量变化曲线比较平滑，供热抽汽量瞬时值最大为514.3 t/h，最小为128 t/h。储热罐提供全部供热负荷模式中供热抽汽量变化曲线有两次突变，一次是在04:18时抽汽量瞬时值从0突增到327.5 t/h，另外一次是在16:36时抽汽量瞬时值降低到0 t/h，并在0抽汽状态持续了3 h。

2) 在相同电、热负荷条件下，储热罐提供部分供热负荷模式下的储热罐最小容量为401.51 t，储热罐提供全部供热负荷模式下的储热罐最小容量2 352.45 t。

3) 相对于储热罐提供部分供热负荷模式，储热罐提供全部供热负荷模式中储热罐的平均放热速度较大，但对储热罐参数要求也更高。

4)在相同电、热负荷条件下，储热罐提供部分供热负荷模式的平均等价煤耗为370.42 g/kWh，储热罐提供全部供热负荷模式的平均等价煤耗为357.17 g/kWh，储热罐提供全部供热负荷模式热经济性更好。