充填料浆对变径管的冲蚀磨损分析

王忠昶，陈 阳，孙 剑，夏洪春

(1.大连交通大学 交通运输工程学院，辽宁 大连 116028；2. 大连大学 建筑工程学院，辽宁 大连 116622)

冲蚀磨损是矿山采空区进行回填工作中输送管道存在的最典型失效模式，也是制约充填设备长周期运行的一个重要原因[1-3]。故探索管道磨损区域和磨损程度对确保管道输送效率和矿山充填安全具有重要意义。在实际工业生产过程中，经常使用变径管来达到控制料浆流量和保护运输管道的目的。料浆输送时变径管的存在会导致料浆输送状态发生瞬时变化，此时管壁所受到的磨损程度要比在正常管道中严重数十倍，管道失效几率加大。因此根据输送管道的几何参数准确预测管道磨损区域和磨损程度，可对关键部位优化设计提供参考。

近年来，众多学者采用数值模拟的方法来研究冲蚀磨损。乔智威等[4]使用Fluent软件研究了水沙流作用下粗糙度对圆柱体结构的阻力系数、升力系数和冲蚀率的影响，得出在同一含沙量的水流状况下，圆柱体结构在粗糙度为0.3%时的冲蚀率最大；许爱荣等[5]使用离散相模型模拟液固两相流对三通管道的冲蚀情况，得出分支处磨损的分布规律；石宏伟等[6]借助Fluent软件研究了弯管与水平直管的易磨损位置，将模拟结果与矿山管道壁厚实测结果进行对比，验证了管道磨损数值模拟方法的有效性，并且给出降低充填管道磨损的建议；戚伟等[7]结合理论分析与数值模拟计算，研究了料浆自流输送过程中流速与压力分布规律，并据此得出大冶铁矿输送管道易磨损位置为各拐点处，可通过选择耐磨性较好的弯管和反转水平管道来延长管道的使用寿命。过江等[8]结合某矿山实际充填管道，研究了颗粒尺寸、形状、浆体黏度、流速等因素对管道磨损的影响程度。

目前对于管道冲蚀的研究主要集中普通直管和弯管上，对于变径管等不规则管道的研究很少，且针对煤矸石似膏体充填料浆的管道输送磨损研究尚缺乏。本研究采用离散相模型(discrete phase model,DPM)对煤矸石似膏体充填料浆在变径弯管中的输送进行仿真分析，探讨管道的磨损机理，重点研究管道变径处的磨损规律，切实提高料浆在管道中输送的可行性与安全性。

1 理论模型及控制方程

采用计算机流体力学软件(computational fluid dynamics,CFD)预测管道冲蚀磨损位置是替代试验研究的一种有效方法[9]。本研究将使用欧拉-拉格朗日方法，将粉煤灰和胶凝剂组成的料浆溶液视为连续相，其运动方程采用欧拉法进行求解；将煤矸石颗粒视为离散相，运动方程使用拉格朗日法求解，得出颗粒与管道的碰撞信息，进而预测管道的磨损状况。

1.1 控制方程

所计算的离散相的体积分数相对较小，因此采用离散相模型DPM进行计算。对管道的冲蚀磨损计算过程主要包括：流场、颗粒轨迹以及冲蚀计算[10]。连续相的输送与离散相颗粒的运动存在相互影响的状况，需要考虑两相之间的相互耦合。流体雷诺数Re=190，属层流范畴。因此采用适用范围广、计算精度更高的Laminar层流模型[11]。

连续性方程为：

(1)

动量守恒方程为：

(2)

1.2 离散相控制模型

离散相在料浆中所占的浓度很小，不考虑颗粒之间的相互碰撞，考虑相间的耦合作用以及该作用对两相运动的影响，在此条件下固体颗粒的作用力在笛卡尔坐标系中可表示为[12-14]：

(3)

式中：v为连续相的速度，m/s；vg为颗粒相的速度，m/s；ρg为颗粒密度，kg/m3；ρs为连续相料浆密度，kg/m3；FD(v-vg)为颗粒单位质量曳力，N；Fm为其他质量力，N。

1.3 冲蚀磨损模型

管道冲蚀磨损的影响因素有很多，包括管道的材料性质、颗粒的性质、冲击速度、冲击角度、几何形状等。本研究选取Fluent中定义的冲蚀磨损模型[15]：

(4)

式中：Rerosion为冲蚀磨损率，kg/(m2·s)；p为颗粒数目；mp为颗粒的质量流率，kg/s；f(θ)为冲击角度函数；C(dp)为颗粒的直径函数；μp为颗粒相对壁面的滑移速度，m/s；bv为滑移速度函数；Aface为颗粒冲击面的单元表面积；m2。

1.4 壁面碰撞恢复方程

颗粒进入管道中与管道发生碰撞之后的回弹速度并非一成不变的，由于发生碰撞后存在能量转移与损失，颗粒的回弹速度总是低于入射速度，通常用壁面碰撞恢复函数来表达这一特性，采取Forder等[16]的恢复系数方程：

eN=0.988-0.78α+0.19α2-0.24α3+0.27α4，

(5)

eT=1-0.78α+0.84α2-0.21α3+0.028α4-0.022α5。

(6)

式中：eN代表法向恢复系数方程；eT代表切向恢复方程；α为颗粒的冲击角度。

2 计算问题描述

2.1 几何模型及其网格

使用ANSYS中GAMBIT模块建立变径弯管，由入口段G1、弯管段G2、平流段G3、变径段G4、出口段G5组成，管道材料采用Fluent软件中默认材料(无碳不锈钢)。R1代表入口管径，R2代表出口管径，具体参数如图1所示。经无关性检验之后使用自带网格划分工具MESH对变径弯管划分网格如图1。

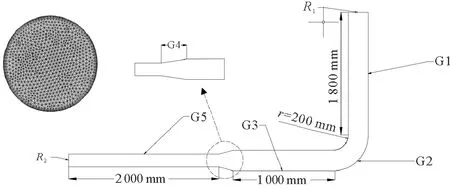
图1 变径弯管平面图与网格划分示意图Fig. 1 Schematic diagram of plan view and grid division ofreducing elbowpipe

2.2 两相模型设置

模拟设置的充填料浆质量配比为煤矸石∶粉煤灰∶胶凝剂=26∶10∶3，将粉煤灰和胶凝剂组成的料浆溶液密度设置为1 900 kg/m3，初始剪切应力τR为81.7 Pa，塑性黏度为2.88 Pa·s[17]；煤矸石密度设置为2 300 kg/m3，粒径选择为随机分布，粒径范围为0.000 1～0.001 m，平均粒径为0.000 5 m。

2.3 边界条件设置

选择速度入口(velocity-inlet)与压力出口(pressure-outlet)，矸石颗粒接触条件为逃离(escape),所选管道内壁为均匀砂粒状表面，因此粗糙度系数默认设置为0.5[18]，壁面边界条件类型为反弹(reflect)，离散相连续相初始速度均设置为1.44 m/s。

3 计算结果分析

3.1 出入口管径比对管道磨损的影响

根据《煤炭工业矿井设计规范：GB 50215—2015》[19]可知，胶结充填管道直径必须大于输送物料最大粒径的5倍，并且对实际矿山充填情况调查得到料浆充填管道直径大多在120～200 mm范围内选取。定义S为出入口管径比(R2/R1)，设定8种不同管径比工况(分别为0.60、0.65、0.70、0.75、0.80、0.85、0.90、0.95)进行研究。图2给出了不同出入口管径比时变径弯管的磨损状况，可见：

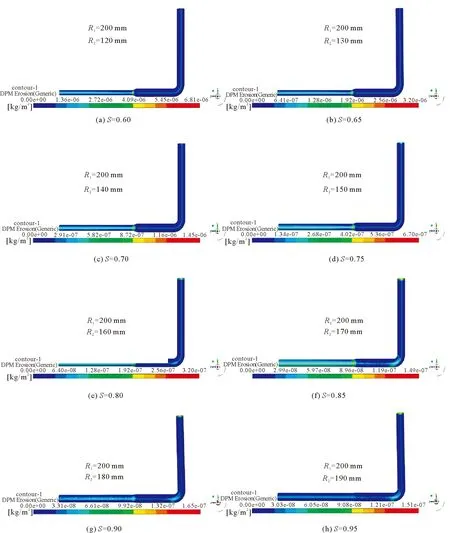
图2 不同出入口管径比下的变径弯管的磨损示意图Fig. 2 Wear of the reducing elbow under different inlet and outlet pipe diameter ratios

1) 磨损位置主要分布在入口处、弯管处、变径管处与出口平流段；

2) 入口处的磨损率随着出入口管径比的增大逐渐增加，最大磨损位置出现在变径段处。当管径比超过0.85时，最大磨损位置转移至入口处。管径比超过0.80时，弯管内外壁磨损明显增加；管径比为0.85时管道磨损最严重、磨损面积最大；

3) 出入口管径比增大时，管道的磨损位置基本保持不变，出口段磨损面积逐步增大且磨损率与平流段相比严重的多。当出入口管径比增大至0.85后磨损面积呈递减趋势，主要原因是变径段两端管径接近，速度与压力变化梯度小，料浆流态相对平稳。

图3给出了变径弯管内的流核变化图。

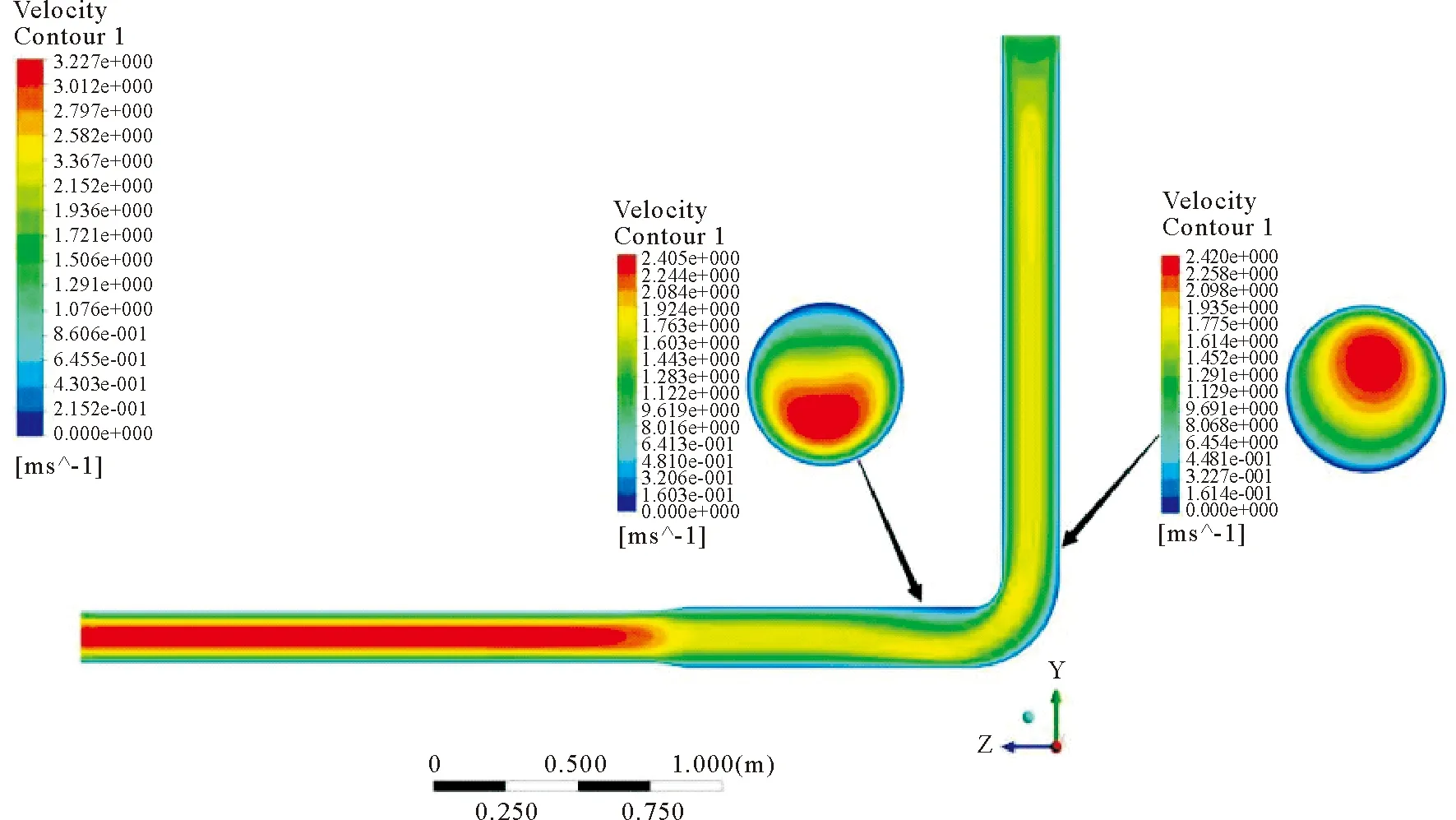
图3 流核变化图Fig. 3 Changeof flow core

1) 弯管段的磨损位置主要分布在弯管内壁15°与弯管出口段底部。主要原因是受离心力和连续相黏度的影响，料浆进入弯管后“流核”在弯管入口15°处向内偏移，将要流出弯管段时“流核”向外侧偏移，导致弯管内壁处与弯管出口段底部流速增快，矸石颗粒与管道碰撞概率增加使得磨损高于其他弯管区域。

2) 变径处的磨损集中在与出口段衔接处。主要原因是变径和二次流的存在使得矸石颗粒密集度增加，颗粒与管壁的接触频繁，导致此处磨损最为严重，总体上变径段处的磨损面积随着出口管径的增大逐步扩大，最大磨损率逐渐降低。

图4给出了入口管径为200 mm，出口管径不同时的磨损率变化曲线。由图4可见，最大磨损率随出入口管径比的增大呈先稳步下降、后保持平稳的趋势。主要原因是出入口管径比小于0.80时，磨损严重位置位于变径段与出口段衔接处，料浆流经变径段受到的管径限制作用降低，流速变动幅度减小，使得管道的最大磨损率持续下降；而当管径比增大至0.80后，磨损严重位置转移至入口处且输送参数保持恒定，因而最大磨损率变化较为平稳。

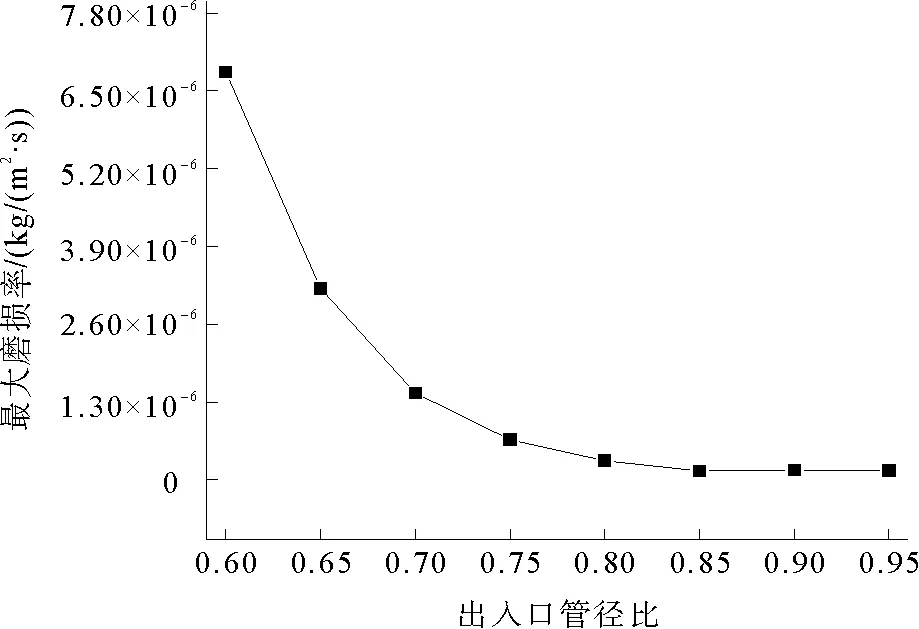
图4 不同出入口管径比下的磨损率变化图Fig. 4 Change of wear rate under different inlet and outlet pipe diameter ratios

3.2 变径段长度对管道磨损的影响

设定5种变径段长度工况(分别为40、80、120、160和200 mm)，变径段长度为图1中G4所示。图5给出了管径比分别为0.65、0.70、0.75时，不同变径段长度下的管道磨损率变化曲线。

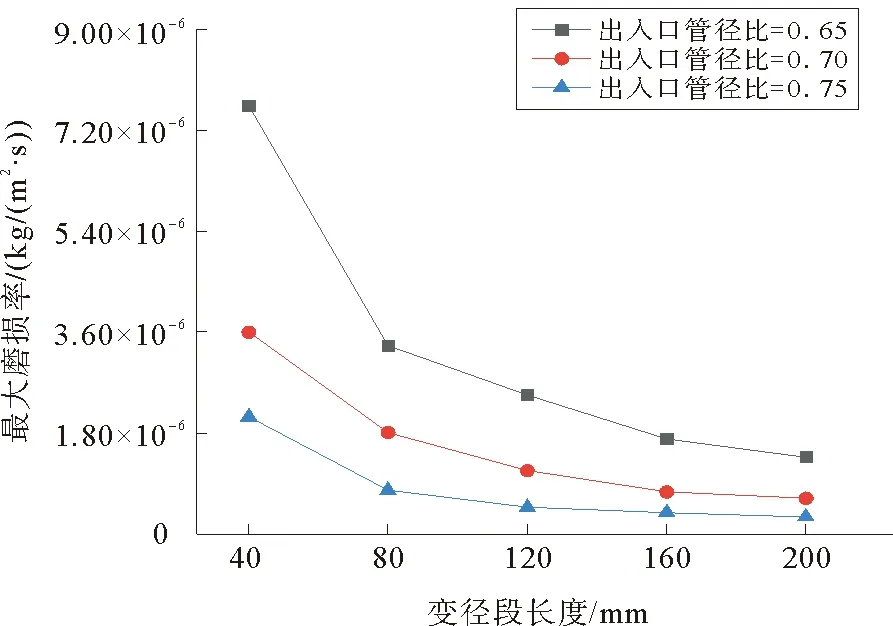
图5 不同变径段长度下的管道磨损率变化图Fig. 5 Change of pipeline wear rate under different reducingsection lengths

1) 变径段的长度对管道磨损率有明显影响，长度在80 mm以下变化对管道磨损影响最大，磨损率随变径管长度增加呈指数性下降趋势。主要原因是从平流段进入变径段时，压强沿管道方向迅速降低，外围料浆流速改变高于中心位置，导致料浆运动状态发生急速变化。变径段长度越小管道的横截面积就越小，矸石颗粒的密集程度、冲击角度和速度就越大，磨损程度就越高。

2) 当变径段长度处于80～160 mm时,磨损率随变径段长度增加稳步下降；当变径段长度超过160 mm后，磨损率大小基本不受变径段长度变化影响。主要原因是变径段长度增大后，颗粒在流道变化区域的运动可以有较长的缓冲，使得料浆在该段的流动较平缓，从而减缓对管道的冲蚀磨损。

3.3 弯管段角度对管道磨损的影响

图6给出了入口管径为200 mm，出口管径为160 mm时不同弯曲角度下的弯管的磨损状况。

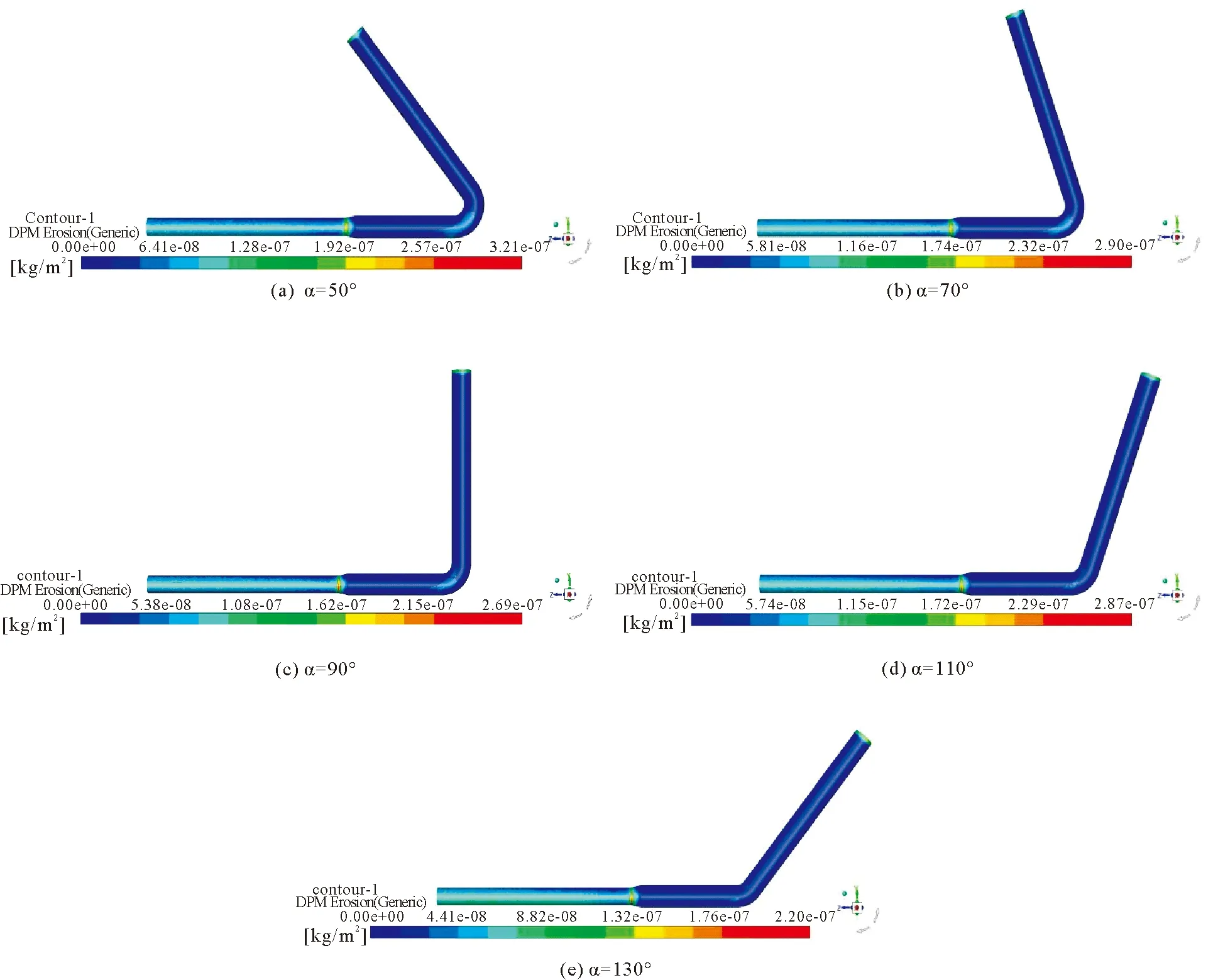
图6 不同弯曲角度下的磨损示意图Fig. 6 Wear under different bending angles

1) 弯曲角度对管道磨损的影响主要体现在弯管段，50°弯管磨损位置集中在弯管内管壁与弯管出口处。随着弯曲角度增大，内壁面磨损位置下移，弯管出口位置磨损面积迅速减小。主要原因是弯曲角度增加后，弯曲流道长度减小，颗粒相由外壁面撞击后反弹的角度变小，使得颗粒与内壁面撞击位置整体下移且几率降低，导致内壁面磨损位置下移。另外弯曲角度的增加使得颗粒运动状态受管道形状影响降低，主动流与二次流作用减弱。矸石颗粒集中在中间部分，流经弯管后与弯管出口底部位置接触减少，对管壁的磨损逐渐降低。

2) 入口处最大磨损位置随管道角度变化从入口左侧偏移至入口右侧。主要原因是料浆刚进入管道时，流体携带作用弱，颗粒相受重力影响严重，这会加剧对垂直于重力方向管壁的磨损。

图7给出了不同弯曲角度下的管道磨损率变化曲线，可见：弯管角度变化对管道磨损影响敏感程度较弱，最大磨损率随弯曲角度变化呈现小幅度波动，当弯曲角度超过90°时最大磨损率出现回升趋势。主要原因是料浆在弯管内流动导致的流态变化经过平流段缓冲后开始趋向稳定，到达变径段时的流态仅存在小幅度变化，因此管道磨损率起伏变化较小。

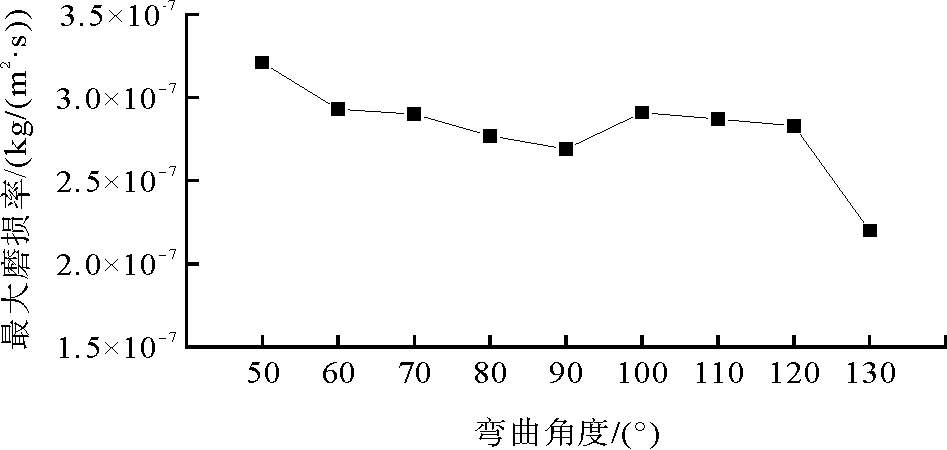
图7 不同弯曲角度下的磨损率变化图Fig. 7 Change of wear rate under different bending angles

4 结论

1) 输送管道的出入口管径比从0.60增至0.95时，入口段与弯管段磨损状况逐渐加重，且弯管段的磨损位置集中分布在内壁面与弯管出口底端，变径段的磨损率大小随管径比变化逐渐增大。出入口管径比为0.60时管道局部磨损最严重；管径比为0.85时管道整体磨损最严重，磨损面积最大。因此在进行矿山实际充填时，如果其管路存在变径管，可适当增加出入口的管径比，且选择合适的管径。

2) 变径段长度由40 mm增至200 mm时，磨损率下降明显，磨损位置由变径段末端向出口段蔓延，磨损面积逐步扩大。变径段长度在80 mm以下时管道冲蚀磨损所受影响最大，超过160 mm后基本不受变径段长度变化影响。采用变径管进行矿山充填时，可以适当延长变径段的长度，并增加该段管道的壁厚。

3) 弯管段角度由50°增至130°时，对管道磨损影响主要体现在弯管段与入口段。弯管内壁磨损位置随弯曲角度增大逐渐下移，弯管出口段底部磨损面积逐渐减小并出现左移的趋势，入口段最大磨损位置受重力影响呈现左右偏移趋势。因此，在设计不同角度变径弯管进行矿山充填时，应尽量增大弯曲角度，延长平流段的长度，从而减弱弯曲角度对管道磨损的影响。